こんにちは、ひかりです。
今回はベクトル解析から曲率・捩率とフレネ・セレーの公式について解説していきます。
この記事では以下のことを紹介します。
- 位置ベクトルと曲線の長さについて
- 曲率と捩率について
- フレネ・セレーの公式について
位置ベクトルと曲線の長さ
ベクトル解析02の記事にて、1変数のベクトル値関数について紹介しました。
実は、3次元空間上の曲線は1変数のベクトル値関数を用いて表現することができます。
(2次元平面上の曲線についても同様に表現できます。)
そのベクトル値関数のことを位置ベクトルといい、次のように与えられます。
3次元空間上の曲線 \( C \) をパラメータ \( t \) で媒介変数表示
$$ \begin{cases} x=x(t) \\ y=y(t) \\ z=z(t) \end{cases} $$
をする。このとき、曲線 \( C \) の動点 \( P \) の座標は原点からのベクトル値関数
$$ \mathbf{p}(t)=(x(t),y(t),z(t)) $$
で表現することができる。
この \( \mathbf{p}(t) \) を位置ベクトルという。
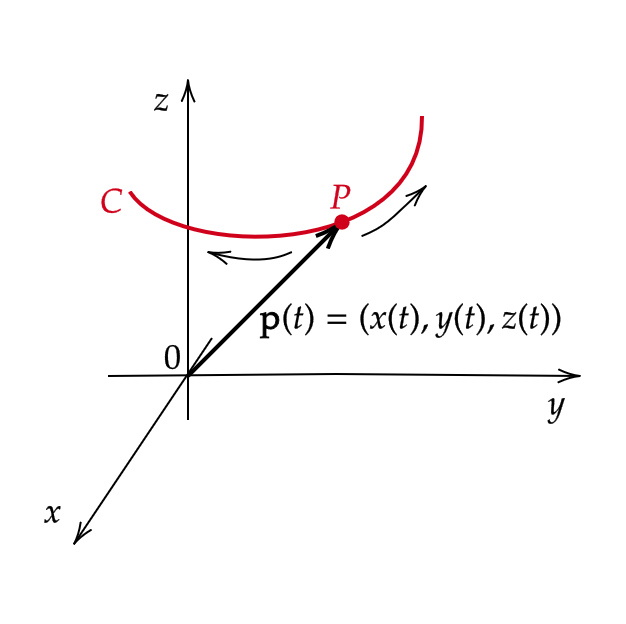
微分が曲線の接線の傾きを表すことから、次を定めることができます。
曲線 \( C \) の位置ベクトル
$$ \mathbf{p}(t)=(x(t),y(t),z(t)) $$
に対して、パラメータ \( t \) で微分した導関数
$$ \mathbf{p}'(t)=(x'(t),y'(t),z'(t)) $$
を曲線 \( C \) 上の点 \( P \) における接線ベクトルという。
また接線ベクトル \( \mathbf{p}'(t) \) をその大きさ \( \|\mathbf{p}'(t)\| \) で割ったベクトル
$$ \mathbf{t}=\frac{\mathbf{p}'(t)}{\|\mathbf{p}'(t)\|} $$
を単位接線ベクトルという。
この接線ベクトルを用いることにより、パラメータ \( t \) の区間 \( [a,b] \) における曲線 \( C \) の長さを求めることができます。
まず、区間 \( [s_1,s_2] \) における曲線 \( C \) の長さ \( s \) は微分積分学15より次のようになります。
$$ s=\int_{s_1}^{s_2}ds=\int_{s_1}^{s_2} \sqrt{(dx)^2+(dy)^2+(dz)^2} $$
ただし、 \( s_1,s_2 \) は \( s:s_1\to s_2 \) のとき \( t:a\to b \) に対応するものとする。
(微分積分学15では2次元平面で解説していますが、3次元空間でも同様です)
これを計算していくと、
$$ \begin{align} s&=\int_{s_1}^{s_2} \sqrt{(dx)^2+(dy)^2+(dz)^2} \\ &=\int_a^b \sqrt{\left( \frac{dx}{dt} \right)^2+\left( \frac{dy}{dt} \right)^2+\left( \frac{dz}{dt} \right)^2}dt \\ &=\int_a^b\sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt=\int_a^b\|\mathbf{p}'(t)\| dt \end{align} $$
まとめると、
パラメータ \( t \) の区間 \( [a,b] \) における曲線 \( C \) の長さ \( s \) は、その接線ベクトル \( \mathbf{p}'(t) \) を用いて次のように表すことができる。
$$ s=\int_a^b\|\mathbf{p}'(t)\|dt=\int_a^b\sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt $$
(1) 次の位置ベクトルで与えられる曲線を考える。
$$ \mathbf{p}(t)=(\frac{3}{2}t^2-1,2\sqrt{6}t\sqrt{t},9t+3) $$
まず、接線ベクトルは
$$ \mathbf{p}'(t)=(3t,3\sqrt{6}\sqrt{t},9) $$
であるので、その大きさ \( \|\mathbf{p}'(t)\| \) は
$$ \begin{align} \|\mathbf{p}'(t)\|&=\sqrt{(3t)^2+(3\sqrt{6}\sqrt{t})^2+9^2}=\sqrt{9t^2+54t+81} \\ &=\sqrt{9(t+3)^2}=3(t+3) \end{align} $$
したがって、単位接線ベクトル \( \mathbf{t} \) は
$$ \mathbf{t}=\frac{\mathbf{p}'(t)}{\|\mathbf{p}'(t)\|}=\frac{1}{3(t+3)}(3t,3\sqrt{6}\sqrt{t},9) $$
であり、 \( 0≦t≦2 \) での曲線の長さ \( s \) は
$$ s=\int_0^2\|\mathbf{p}'(t)\|dt=\int_0^23(t+3)dt=24 $$
(2) 次の位置ベクトルで与えられる曲線を考える。
$$ \mathbf{p}(t)=(3\cos t,3\sin t,t) $$
まず、接線ベクトルは
$$ \mathbf{p}'(t)=(-3\sin t,3\cos t,1) $$
であるので、その大きさ \( \|\mathbf{p}'(t)\| \) は
$$ \begin{align} \|\mathbf{p}'(t)\|&=\sqrt{(-3\sin t)^2+(3\cos t)^2+1^2}=\sqrt{10} \end{align} $$
したがって、単位接線ベクトル \( \mathbf{t} \) は
$$ \mathbf{t}=\frac{\mathbf{p}'(t)}{\|\mathbf{p}'(t)\|}=\frac{1}{10}(-3\sin t,3\cos t,1) $$
であり、区間 \( [0,t]\) での曲線の長さ \( s \) は
$$ s=\int_0^t\|\mathbf{p}'(r)\|dr=\int_0^t\sqrt{10}dr=\sqrt{10}t $$
最後に、位置ベクトル \( \mathbf{p}(t) \) を曲線の長さ \( s \) による関数で表してみましょう。
まず、パラメータ \( t \) の区間 \( [a,t] \) における曲線 \( C \) の長さ \( s \) は定理1より、
$$ s=\int_a^t\|\mathbf{p}'(r)\|dr \ (=f(t)とおく) $$
よって、両辺を \( t \) で微分すると、
$$ \frac{ds}{dt}=\|\mathbf{p}'(t)\| $$
したがって、 \( \frac{ds}{dt}=\|\mathbf{p}'(t)\|>0 \) より \( s \) は区間 \( [a,t] \) 上で \( t \) の狭義単調増加となるので、 \( s=f(t) \) は単射となります。
(とくに、 \( f \) の終域を区間 \( [a,t] \) 上の \( f \) の値域に制限することにより、区間 \( [a,t] \) 上で全単射となります)
よって、 \( s=f(t) \) の逆関数 \( t=f^{-1}(s) \) が存在します。
したがって、
$$ \mathbf{p}(t)=\mathbf{p}(f^{-1}(s)) $$
このとき、 \( \mathbf{p}(f^{-1}(s)) \) も単に \( \mathbf{p}(s) \) と表して、
$$ \mathbf{p}=\mathbf{p}(t)=\mathbf{p}(s), \quad (t=f^{-1}(s)) $$
と表すことにします。また、それぞれの接線ベクトルは
$$ \mathbf{p}'(t)=\frac{d\mathbf{p}'(t)}{dt}, \quad \mathbf{p}'(s)=\frac{d\mathbf{p}'(s)}{ds} $$
となります。(微分の変数も変わることに注意してください。)
例1(2)の曲線を考える。つまり、
$$ \mathbf{p}(t)=(3\cos t,3\sin t,t) $$
区間 \( [0,t]\) での曲線の長さ \( s \) は \( s=\sqrt{10}t \) であったので、 \( t=\frac{s}{\sqrt{10}} \)
したがって、
$$ \mathbf{p}(s)=\left(3\cos \frac{s}{\sqrt{10}},3\sin \frac{s}{\sqrt{10}},\frac{s}{\sqrt{10}}\right) $$
最後に、ひとつ単位接線ベクトルに関する公式を紹介します。
曲線 \( C \) の単位接線ベクトル \( \mathbf{t} \) に対して、次が成り立つ。
$$ \mathbf{t}=\mathbf{p}'(s) $$
定理2の証明(気になる方だけクリックしてください)
上の計算より、 \( \frac{ds}{dt}=\|\mathbf{p}'(t)\| \) であるので、
$$ \begin{align} \mathbf{p}'(s)&=\frac{d\mathbf{p}(s)}{ds}=\frac{dt}{ds}\cdot \frac{d\mathbf{p}(s)}{dt}=\frac{dt}{ds}\cdot \frac{d\mathbf{p}(t)}{dt} \ (記法に注意) \\ &=\frac{1}{\|\mathbf{p}'(t)\|}\cdot \mathbf{p}'(t)=\mathbf{t} \end{align} $$
曲率と捩率
まず、単位接線ベクトルから単位主法線ベクトルと単位従法線ベクトルを定義しましょう。
曲線 \( C \) の単位接線ベクトル \( \mathbf{t} \) は \( \|\mathbf{t}\|=1 \) であるので、ベクトル解析02の定理2より、
$$ \mathbf{t}\cdot \mathbf{t}’=0 $$
をみたす。このベクトル \( \mathbf{t}’ \) のことを主法線ベクトルという。
(これは定理2より、 \( \mathbf{t}’=\mathbf{p}^{\prime\prime}(s) \) で与えられる)
また主法線ベクトル \( \mathbf{t}’ \) をその大きさ \( \|\mathbf{t}’\| \) で割ったベクトル
$$ \mathbf{n}=\frac{\mathbf{t}’}{\|\mathbf{t}’\|} $$
を単位主法線ベクトルという。
さらに、曲線 \( C \) の単位接線ベクトル \( \mathbf{t} \) と単位主法線ベクトル \( \mathbf{n} \) に対して、
$$ \mathbf{b}=\mathbf{t}\times \mathbf{n} $$
となるベクトル \( \mathbf{b} \) のことを単位従法線ベクトルという。
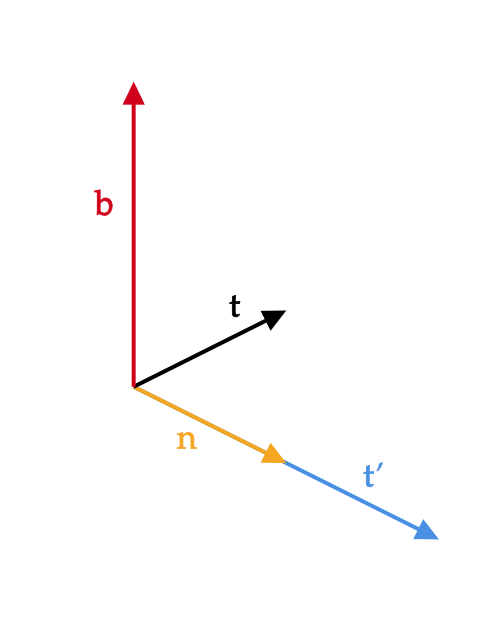
これらをもとにして、曲線 \( C \) の曲がり具合を表す曲率とねじれ具合を表す捩率(れいりつ)を定義します。
曲線 \( C \) の主法線ベクトル \( \mathbf{t}’ \) に対して、その大きさ \( \|\mathbf{t}’\| \) のことを曲線 \( C \) の曲率といい、 \( \kappa \) と表す。
また、曲線 \( C \) の単位主法線ベクトル \( \mathbf{n} \) と単位従法線ベクトル \( \mathbf{b} \) に対して、
$$ \tau=\mathbf{b}\cdot \mathbf{n}’ $$
のことを曲線 \( C \) の捩率という。
半径 \( r \) の円を考える。つまり、
$$ x^2+y^2=r^2 $$
この曲線の位置ベクトルは
$$ \mathbf{p}(t)=(r\cos t,r\sin t,0) $$
であるので、接線ベクトルは
$$ \mathbf{p}'(t)=(-r\sin t,r\cos t,0) $$
\( \|\mathbf{p}'(t)\|=r \) より、曲線の長さ \( s \) は
$$ s=\int_0^t\|\mathbf{p}'(u)\|du=rt $$
したがって、 \( t=\frac{s}{r} \) より、
$$ \mathbf{p}(s)=\left(r\cos \frac{s}{r},r\sin \frac{s}{r},0\right) $$
$$ \mathbf{p}'(s)=\left(-\sin \frac{s}{r},\cos \frac{s}{r},0 \right) $$
$$ \mathbf{p}^{\prime\prime}(s)=\left( -\frac{1}{r}\cos \frac{s}{r},-\frac{1}{r}\sin \frac{s}{r},0 \right) $$
よって、曲率 \( \kappa \) は
$$ \kappa=\|\mathbf{p}^{\prime\prime}(s)\|=\frac{1}{r} $$
また、
$$ \mathbf{t}=(-\sin t,\cos t,0), \quad \mathbf{n}=(-\cos t,-\sin t,0) $$
より、単位従法線ベクトルは
$$ \mathbf{b}=\begin{pmatrix} -\sin t \\ \cos t \\ 0 \end{pmatrix}\times \begin{pmatrix} -\cos t \\ -\sin t \\ 0 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$
したがって、捩率 \( \tau \) は
$$ \tau=(0,0,1)\cdot (\sin t,-\cos t,0)=0 $$
まとめると、半径 \( r \) の円の曲率は \( \frac{1}{r} \) 、捩率は \( 0 \) となる。
フレネ・セレーの公式
曲率と捩率を用いることにより、単位接線ベクトル・単位主法線ベクトル・単位従法線ベクトルの \( s \) による導関数を求めることができます。
3次元空間上の曲線 \( C \) の単位接線ベクトル \( \mathbf{t}(s) \) 、単位主法線ベクトル \( \mathbf{n}(s) \) 、単位従法線ベクトル \( \mathbf{b}(s) \) 、曲率 \( \kappa(s) \) 、捩率 \( \tau(s) \) に対して、次が成り立つ。
(1) \( \mathbf{t}'(s)=\kappa(s)\mathbf{n}(s) \)
(2) \( \mathbf{n}'(s)=-\kappa(s)\mathbf{t}(s)+\tau(s)\mathbf{b}(s) \)
(3) \( \mathbf{b}'(s)=-\tau(s)\mathbf{n}(s) \)
これはつまり、
$$ \frac{d}{ds} \begin{pmatrix} \mathbf{t} \\ \mathbf{n} \\ \mathbf{b} \end{pmatrix}=\begin{pmatrix} 0 & \kappa & 0 \\ -\kappa & 0 & \tau \\ 0 & -\tau & 0 \end{pmatrix}\begin{pmatrix} \mathbf{t} \\ \mathbf{n} \\ \mathbf{b} \end{pmatrix} $$
定理3の証明(気になる方だけクリックしてください)
(1) 単位主法線ベクトル \( \mathbf{n} \) と曲率 \( \kappa \) の定義より、
$$ \mathbf{n}(s)=\frac{\mathbf{t}'(s)}{\|\mathbf{t}'(s)\|}=\frac{\mathbf{t}'(s)}{\kappa(s)} $$
となるので、 \( \mathbf{t}'(s)=\kappa(s)\mathbf{n}(s) \)
(3) 単位従法線ベクトル \( \mathbf{b} \) を \( s \) で微分すると、ベクトル値関数の微分公式より、
$$ \begin{align} \mathbf{b}’&=(\mathbf{t}\times \mathbf{n})’=\mathbf{t}’\times \mathbf{n}+\mathbf{t}\times \mathbf{n}’ \\ &=(\kappa \mathbf{n})\times \mathbf{n}+\mathbf{t}\times \mathbf{n}’ \quad ((1)より) \\ &=\mathbf{t}\times \mathbf{n}’ \quad (第1項は0) \end{align} $$
したがって、 \( \mathbf{b}’ \) と \( \mathbf{t} \) は直交します。
また、 \( \|\mathbf{b}\|=1 \) であるので、ベクトル解析02の定理2より、
$$ \mathbf{b}\cdot\mathbf{b}’=0 $$
となるので、 \( \mathbf{b} \) と \( \mathbf{b}’ \) は直交します。
よって、 \( \mathbf{b}’ \) は \( \mathbf{t},\mathbf{b} \) に直交するので、
$$ \begin{align} \mathbf{b}'(s)&=(\mathbf{t}\cdot \mathbf{b}’)\mathbf{t}(s)+(\mathbf{b}’\cdot\mathbf{n})\mathbf{n}(s)+(\mathbf{b}\cdot\mathbf{b}’)\mathbf{b}(s)=(\mathbf{b}’\cdot\mathbf{n})\mathbf{n}(s) \end{align} $$
ここで、
$$ 0=(\mathbf{b}\cdot\mathbf{n})’=\mathbf{b}’\cdot\mathbf{n}+\mathbf{b}\cdot\mathbf{n}’=\mathbf{b}’\cdot\mathbf{n}+\tau(s) $$
より、 \( -\tau(s)=\mathbf{b}’\cdot \mathbf{n} \) となるので、
$$ \mathbf{b}'(s)=-\tau(s)\mathbf{n}(s) $$
(2) (1)と(3)およびベクトル値関数の微分公式より、
$$ \begin{align} \mathbf{n}’&=(\mathbf{b}\times \mathbf{t})’=\mathbf{b}’\times \mathbf{t}+\mathbf{b}\times \mathbf{t}’ \\ &=-\tau \mathbf{n}\times \mathbf{t}+\kappa \mathbf{b}\times \mathbf{n}=\tau \mathbf{t}\times \mathbf{n}-\kappa \mathbf{n}\times \mathbf{b} \\ &=-\kappa \mathbf{t}+\tau \mathbf{b} \end{align} $$
となるので、
$$ \mathbf{n}'(s)=-\kappa(s)\mathbf{t}(s)+\tau(s)\mathbf{b}(s) $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

