こんにちは、ひかりです。
今回は確率・統計から正規母集団の母平均の仮説検定について解説していきます。
この記事では以下のことを紹介します。
- 仮説検定について
- 分散既知の場合における正規母集団の母平均の仮説検定について
- 分散未知の場合における正規母集団の母平均の仮説検定について
仮説検定
仮説検定の流れ
母数 \( \theta \) をもつ母集団に対して、 \( \theta \) に仮説「 \( \theta \) がある値 \( \theta_0 \) に等しい」を立てて、この仮説が妥当なものかどうかを抽出した標本から判断する方法のことを仮説検定といいます。
ここでは、一般的な仮説検定の流れについて紹介していきたいと思います。
仮説検定をする際に設定する仮説のことを帰無(きむ)仮説といい、 \( H_0 \) で表します。
仮説「 \( \theta \) がある値 \( \theta_0 \) に等しい」は次のように表せます。
$$ H_0 : \theta=\theta_0 $$
一方で、帰無仮説 \( H_0 \) が妥当でないと判断されたとき採用される仮説を対立仮説といい、 \( H_1 \) で表します。
\( H_0 : \theta=\theta_0 \) のときの対立仮説は次の3つが考えられます。
$$ H_1:\theta\not=\theta_0, \quad H_1:\theta>\theta_0, \quad H_1:\theta<\theta_0 $$
(例えば、 \( \theta \) が \( \theta_0 \) より小さいのではないかと疑っているときは \( H_1:\theta<\theta_0 \) を用います)
とくに、1つ目の対立仮説のことを両側対立仮説、2つ目と3つ目の対立仮説のことを片側対立仮説といいます。
帰無仮説を妥当でないと判断するための基準として、有意水準 \( \alpha \) を定めます。
帰無仮説 \( H_0 \) を仮定したときに、抽出した標本の実現値が起こる確率がこの \( \alpha \) より小さいとき、帰無仮説を妥当でないと判断します。
\( \alpha \) としてはよく \( 0.05 \) や \( 0.01 \) が用いられます。
考えている未知母数 \( \theta \) と標本 \( X_1,\cdots,X_n \) に応じた統計量 \( T=T(\theta;X_1,\cdots,X_n) \) を選びます。
この統計量を検定統計量といいます。
そして、帰無仮説 \( H_0 \) が成り立つときの、検定統計量 \( T \) の確率分布を求めます。
設定した検定統計量 \( T \) に対して、
$$ P(T(\theta;X_1,\cdots,X_n)\in R)=\alpha $$
となる区間 \( R \) を定めます。
この \( R \) を有意水準 \( \alpha \) の棄却域といいます。
棄却域 \( R \) の定め方は考えている対立仮説 \( H_1 \) によって次のように変わります。
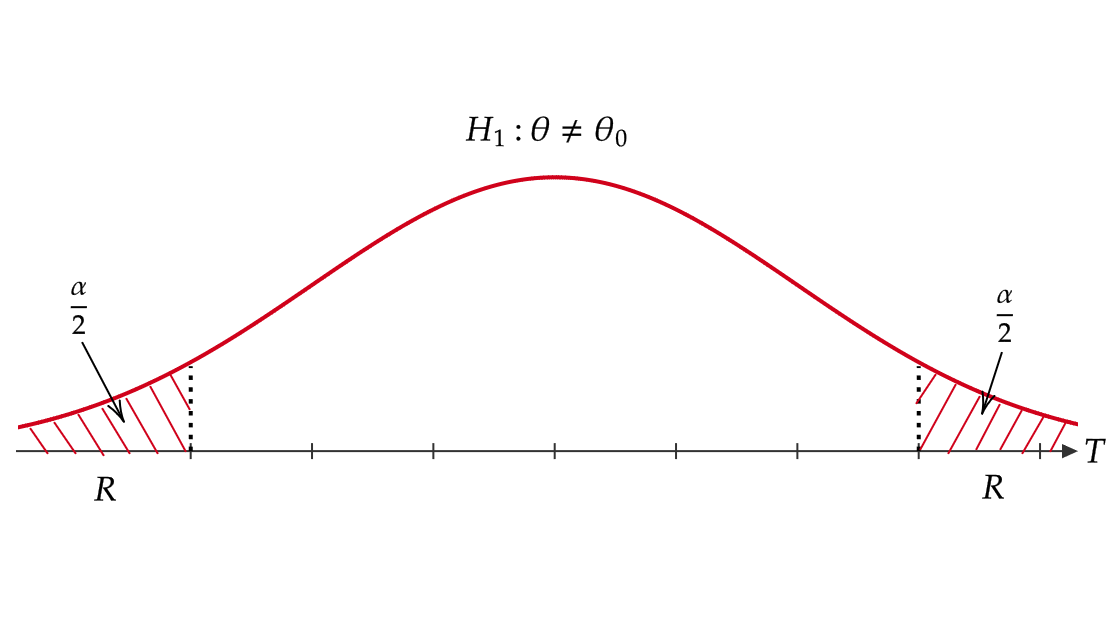
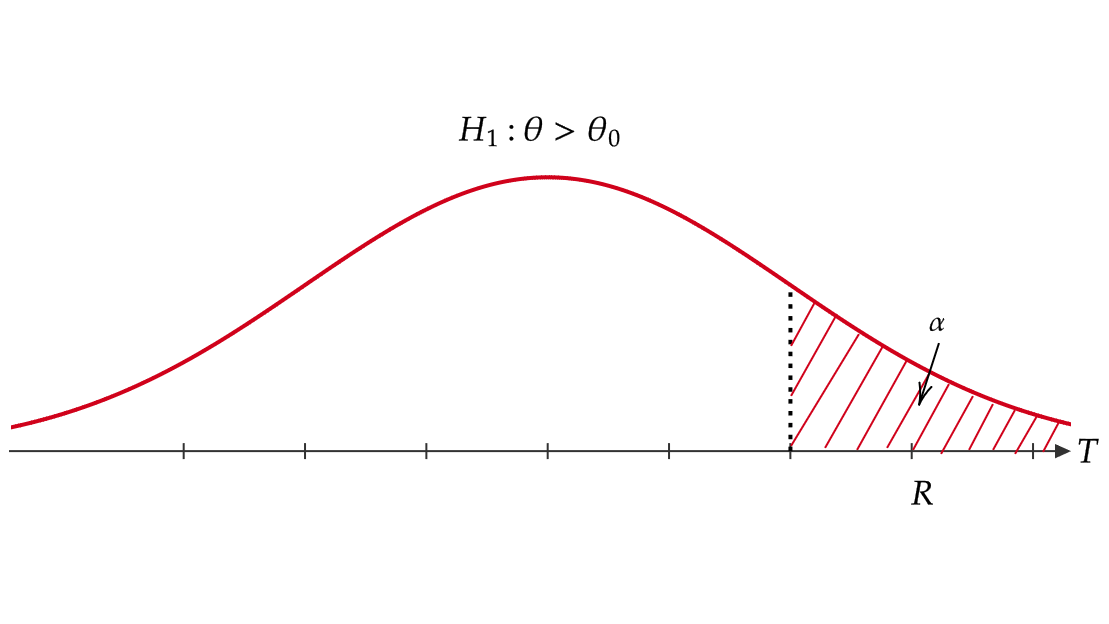
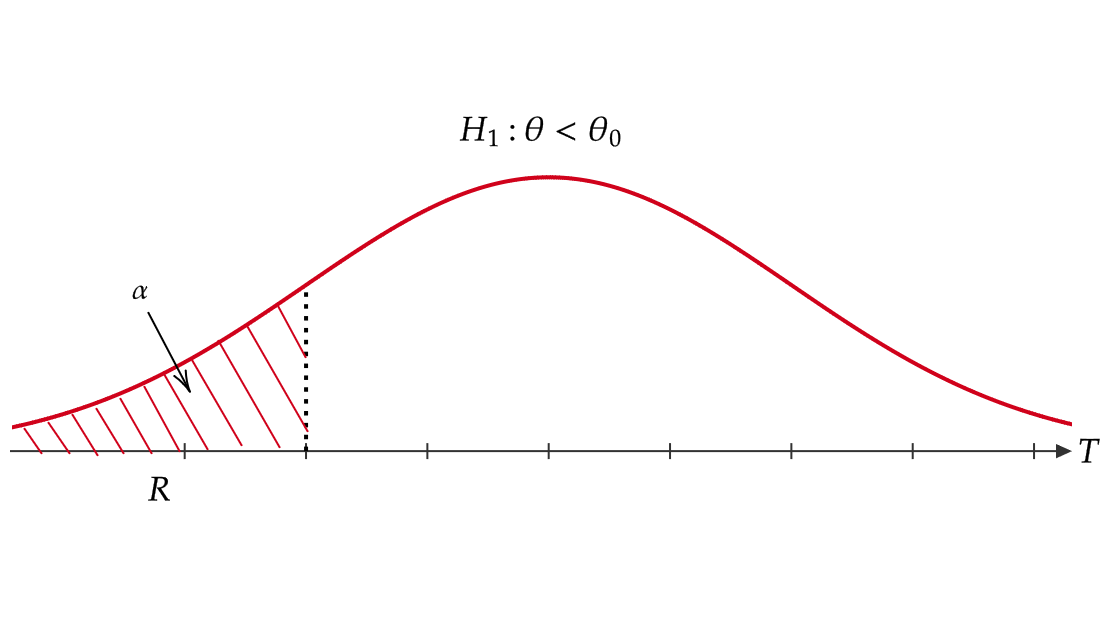
したがって、 \( H_1:\theta\not=\theta_0 \) のときは両側検定、 \( H_1:\theta>\theta_0 \) のときは右片側検定、 \( H_1:\theta<\theta_0 \) のときは左片側検定といいます。
最後に、標本の実現値 \( x_1,\cdots,x_n \) に対して、設定した検定統計量の実現値 \( T^*=T(\theta;x_1,\cdots,x_n) \) を求めます。
それが \( T^*\in R \) ならば帰無仮説 \( H_0 \) は間違っているとして棄却して、 \( T^*\not\in R \) ならば帰無仮説 \( H_0 \) は棄却されない(このことを \( H_0 \) を受容または採択するといいます)という判定を行います。
とくに、帰無仮説 \( H_0 \) が棄却されるとき、この仮説検定は有意である、または有意な差があるといいます。
ただし、注意として帰無仮説 \( H_0 \) が受容されたときは、帰無仮説 \( H_0 \) が正しいと言っているわけではありません。
(あくまで、棄却するだけの証拠を見つけられなかっただけです)
コインを8回投げて表が8回出た。
このとき、このコインの表がでる確率が \( \frac{1}{2} \) であるといえるかどうかを有意水準 \( 0.01 \) で検定する。
このコインの表がでる確率を \( p \) とおく。
(これが今回考えている母数(母比率)である)
まず、帰無仮説を \( H_0:p=\frac{1}{2} \) とおき、対立仮説を \( H_1:p\not=\frac{1}{2} \) とおく。
また、有意水準は \( 0.01 \) である。
ここで、8個の標本 \( X_1,\cdot,X_8 \) を
$$ X_i=\begin{cases} 1 & (i回目に表が出たとき) \\ 0 & (i回目に裏が出たとき) \end{cases} $$
と定めて、検定統計量 \( T \) を
$$ T=T(p;X_1,\cdots, X_8)=\sum_{i=1}^8X_i $$
と定める。
帰無仮説 \( H_0 \) が正しいとすると、 \( T \) は二項分布 \( B(8,\frac{1}{2}) \) に従う。
したがって、 \( T \) の確率関数は
$$ \begin{align} P(T=k)&={}_8C_k\left(\frac{1}{2}\right)^k\left(\frac{1}{2} \right)^{8-k} \\ &=\frac{1}{256}{}_8C_k \ (k=0,1,\cdots,8) \end{align} $$
次に棄却域 \( R \) を求める。
$$ P(T=0)=P(T=8)=0.004, \quad P(T=1)=P(T=7)=0.031 $$
より、
$$ P(T(p;X_1,\cdots,X_8)\in R)=0.01 $$
となる区間(棄却域) \( R \) は
$$ R=(-\infty,1)\cup (7,\infty) $$
ここで、検定統計量 \( T \) の実現値 \( T^* \) を考えると、
$$ T^*=T(p;x_1,\cdots,x_8)=8 $$
であるが、 \( T^*=8\in R \) より \( H_0 \) は棄却される。
したがって、このコインの表がでる確率は \( \frac{1}{2} \) であるとは言えない。
検定の2種類の誤りと検出力
仮説検定を行ったときに、次の2種類の誤りが起きる可能性があります。
1つ目は、本当は帰無仮説 \( H_0 \) が正しいのに棄却してしまう誤りです。
(これは例1の後の注意に述べたことを言っています)
これを第1種の誤りといいます。
2つ目は、本当は帰無仮説 \( H_0 \) が間違っているのに受容してしまう誤りです。
これを第2種の誤りといいます。
第1種の誤りが起きる確率は有意水準 \( \alpha \) となります。
また、第2種の誤りが起きる確率を \( \beta \) とおいたとき、 \( 1-\beta \) のことを検出力といいます。
したがって、仮説検定においては、この2種類の誤りをできるだけ小さくなるように検定の方法を定める必要があります。
しかし、一般的に \( \alpha \) を小さくしようとすると、 \( \beta \) は大きくなってしまいます。
そこで、与えられた有意水準 \( \alpha \) に対して、 \( \beta \) をなるべく小さくするようなものが検定の方法としてはより良いものとなります。
(詳しくは確率・統計26の記事をご覧ください)
分散既知の場合における正規母集団の母平均の仮説検定
それではここからはさまざまな母数 \( \theta \) に応じた仮説検定のやり方について紹介していきます。
この記事では正規分布 \( N(\mu,\sigma^2) \) に従う正規母集団の母平均の仮説検定について見ていきます。
まずは、母分散 \( \sigma^2 \) が既知の場合を考えていきましょう。
初めに、両側検定
$$ H_0:\mu=\mu_0, \quad H_1:\mu\not=\mu_0 $$
を考えます。
このとき、正規母集団から抽出した標本 \( X_1,\cdots,X_n \) に対して、標本平均を \( \displaystyle \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i \) とおくと、確率・統計18の定理1より、
$$ \begin{align} 0.95&=P\left( \overline{X}-1.96\frac{\sigma}{\sqrt{n}}≦\mu_0≦\overline{X}+1.96\frac{\sigma}{\sqrt{n}} \right) \\ &=P\left( -1.96≦\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}}≦1.96 \right) \end{align} $$
となります。したがって、
$$ T=\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} $$
とおくと、有意水準 \( 0.05 \) の両側検定の棄却域 \( R \) は
$$ \begin{align} 0.05&=1-0.95=1-P\left( -1.96≦T≦1.96 \right) \\ &=P(\{ T<-1.96\}\cup\{ T>1.96\}) \end{align} $$
より、
$$ R=\{ T<-1.96\}\cup \{ T>1.96\} $$
となります。同様に有意水準 \( 0.01 \) の両側検定の棄却域 \( R \) は
$$ R=\{ T<-2.58 \} \cup \{ T>2.58 \} $$
まとめると、
母集団が正規分布 \( N(\mu,\sigma^2) \) に従っていて、母分散 \( \sigma^2 \) がわかっているとする。
また、正規母集団から抽出した標本を \( X_1,\cdots,X_n \) として、標本平均を \( \displaystyle \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i \) とおく。
仮説 \( H_0:\mu=\mu_0, \quad H_1:\mu\not=\mu_0 \) に対して、有意水準 \( 0.05,0.01 \) の母平均 \( \mu \) の両側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-1.96\}\cup \{ T>1.96\} $$
$$ 有意水準0.01 \quad R=\{ T<-2.58 \} \cup \{ T>2.58 \} $$
同様に片側検定の場合は次のようになります。
母集団が正規分布 \( N(\mu,\sigma^2) \) に従っていて、母分散 \( \sigma^2 \) がわかっているとする。
また、正規母集団から抽出した標本を \( X_1,\cdots,X_n \) として、標本平均を \( \displaystyle \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i \) とおく。
仮説 \( H_0:\mu=\mu_0, \quad H_1:\mu<(>)\mu_0 \) に対して、有意水準 \( 0.05,0.01 \) の母平均 \( \mu \) の片側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\frac{\overline{X}-\mu_0}{\frac{\sigma}{\sqrt{n}}} $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-1.645\} \ (\{T>1.645\}) $$
$$ 有意水準0.01 \quad R=\{ T<-2.33 \}\ (\{ T>2.33\}) $$
ある工場のある製品は平均重量 \( 10.00 \) (g) 、標準偏差 \( 0.40 \) の正規分布に従うことが知られている。
いま、あるロットから \( 64 \) 個の製品を抽出したところ、平均重量が \( 10.10 \) (g)であった。
このとき、このロットの製品は通常の製品に比べて規格外れであるかどうかを有意水準 \( 0.05 \) で検定する。
まず、帰無仮説を \( H_0:\mu=10.00 \) とおき、対立仮説を \( H_1:\mu\not=10.00 \) とおく。
また、有意水準は \( 0.05 \) である。
帰無仮説 \( H_0 \) が正しいとすると、検定統計量
$$ T=\frac{\overline{X}-10.00}{\frac{0.40}{\sqrt{64}}} $$
は標準正規分布 \( N(0,1) \) に従う。
このとき、定理1より有意水準 \( 0.05 \) の棄却域 \( R \) は
$$ R=\{ T<-1.96\}\cup \{ T>1.96\} $$
となる。
したがって、検定統計量 \( T \) の実現値 \( T^* \) が
$$ T^*=\frac{10.10-10.00}{\frac{0.40}{\sqrt{64}}}=2.00\in R $$
となるので、帰無仮説 \( H_0 \) は棄却される。
よって、このロットの製品は通常の製品に比べて規格外れであるといえる。
分散未知の場合における正規母集団の母平均の仮説検定
分散未知で標本数が十分大きい場合
次に、母分散 \( \sigma^2 \) が未知の場合を考えていきましょう。
母分散が未知であっても、標本数 \( n \) が十分大きい場合(目安は \( n≧30 \) )は標本分散 \( \displaystyle S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 \) が母分散 \( \sigma^2 \) の一致推定量であることから、上の議論で母分散 \( \sigma^2 \) の代わりに標本分散 \( S^2 \) を用いることができます。
したがって、両側検定の棄却域は次のようになります。
母集団が正規分布 \( N(\mu,\sigma^2) \) に従っていて、母分散 \( \sigma^2 \) がわかっていないとする。
また、正規母集団から十分多く(目安は \( n≧30 \))抽出した標本を \( X_1,\cdots,X_n \) として、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
とおく。
仮説 \( H_0:\mu=\mu_0, \quad H_1:\mu\not=\mu_0 \) に対して、有意水準 \( 0.05,0.01 \) の母平均 \( \mu \) の両側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\frac{\overline{X}-\mu_0}{\frac{S}{\sqrt{n}}} $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-1.96\}\cup \{ T>1.96\} $$
$$ 有意水準0.01 \quad R=\{ T<-2.58 \} \cup \{ T>2.58 \} $$
同様に片側検定の場合は次のようになります。
母集団が正規分布 \( N(\mu,\sigma^2) \) に従っていて、母分散 \( \sigma^2 \) がわかっていないとする。
また、正規母集団から十分多く(目安は \( n≧30 \))抽出した標本を \( X_1,\cdots,X_n \) として、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
とおく。
仮説 \( H_0:\mu=\mu_0, \quad H_1:\mu<(>)\mu_0 \) に対して、有意水準 \( 0.05,0.01 \) の母平均 \( \mu \) の片側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\frac{\overline{X}-\mu_0}{\frac{S}{\sqrt{n}}} $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-1.645\} \ (\{T>1.645\}) $$
$$ 有意水準0.01 \quad R=\{ T<-2.33 \}\ (\{ T>2.33\}) $$
分散未知で標本数が少ない場合
母分散が未知であり、かつ標本数が少ない場合には、上の仮説検定は使えないため、別の方法を考えます。
初めに、両側検定
$$ H_0:\mu=\mu_0, \quad H_1:\mu\not=\mu_0 $$
を考えます。
このとき、正規母集団から抽出した標本 \( X_1,\cdots,X_n \) に対して、標本平均を \( \displaystyle \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i \) 、標本分散を \( \displaystyle S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 \) とおくと、確率・統計18の定理3より、
$$ \begin{align} 0.95&=P\left( \overline{X}-t_{0.025}(n-1)\frac{S}{\sqrt{n}}≦\mu_0≦\overline{X}+t_{0.025}(n-1)\frac{S}{\sqrt{n}} \right) \\ &=P\left( -t_{0.025}(n-1)≦\frac{\sqrt{n}(\overline{X}-\mu_0)}{S}≦t_{0.025}(n-1) \right) \end{align} $$
となります。したがって、
$$ T=\frac{\sqrt{n}(\overline{X}-\mu_0)}{S} $$
とおくと、有意水準 \( 0.05 \) の両側検定の棄却域 \( R \) は
$$ \begin{align} 0.05&=1-0.95=1-P\left( -t_{0.025}(n-1)≦T≦t_{0.025}(n-1) \right) \\ &=P(\{ T<-t_{0.025}(n-1)\}\cup\{ T>t_{0.025}(n-1)\}) \end{align} $$
より、
$$ R=\{ T<-t_{0.025}(n-1)\}\cup\{ T>t_{0.025}(n-1)\} $$
となります。同様に有意水準 \( 0.01 \) の両側検定の棄却域 \( R \) は
$$ R=\{ T<-t_{0.005}(n-1)\}\cup\{ T>t_{0.005}(n-1)\} $$
まとめると、
母集団が正規分布 \( N(\mu,\sigma^2) \) に従っていて、母分散 \( \sigma^2 \) がわかっていないとする。
また、正規母集団から抽出した標本を \( X_1,\cdots,X_n \) として、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
とおく。
仮説 \( H_0:\mu=\mu_0, \quad H_1:\mu\not=\mu_0 \) に対して、有意水準 \( 0.05,0.01 \) の母平均 \( \mu \) の両側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\frac{\sqrt{n}(\overline{X}-\mu_0)}{S} $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-t_{0.025}(n-1)\}\cup\{ T>t_{0.025}(n-1)\} $$
$$ 有意水準0.01 \quad R=\{ T<-t_{0.005}(n-1)\}\cup\{ T>t_{0.005}(n-1)\} $$
同様に片側検定の場合は次のようになります。
母集団が正規分布 \( N(\mu,\sigma^2) \) に従っていて、母分散 \( \sigma^2 \) がわかっていないとする。
また、正規母集団から抽出した標本を \( X_1,\cdots,X_n \) として、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
とおく。
仮説 \( H_0:\mu=\mu_0, \quad H_1:\mu<(>)\mu_0 \) に対して、有意水準 \( 0.05,0.01 \) の母平均 \( \mu \) の片側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\frac{\sqrt{n}(\overline{X}-\mu_0)}{S} $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-t_{0.05}(n-1)\} \ (\{T>t_{0.05}(n-1)\}) $$
$$ 有意水準0.01 \quad R=\{ T<-t_{0.01}(n-1) \}\ (\{ T>t_{0.01}(n-1)\}) $$
ある学校の男子高校生6人の身長は次のようであった。
$$ 164, \ 160, \ 165, \ 160, \ 162, \ 161 \ (cm) $$
このとき、この学校の男子高校生の平均身長は \( 165 \) cmの正規母集団からの標本とみなせるのかを有意水準 \( 0.05 \) で検定する。
まず、帰無仮説を \( H_0:\mu=165 \) とおき、対立仮説を \( H_1:\mu\not=165 \) とおく。
また、有意水準は \( 0.05 \) である。
帰無仮説 \( H_0 \) が正しいとすると、検定統計量
$$ T=\frac{\sqrt{6}(\overline{X}-165)}{S} $$
は自由度 \( 5 \) の \( t \) 分布 \( t(5) \) に従う。
このとき、定理1より有意水準 \( 0.05 \) の棄却域 \( R \) は
$$ R=\{ T<-t_{0.025}(5)\}\cup\{ T>t_{0.025}(5)\}=\{ T<-2.571\}\cup\{ T>2.571\} $$
となる。したがって、
$$ \overline{x}=162, \ S^2=3.665 $$
より、検定統計量 \( T \) の実現値 \( T^* \) が
$$ T^*=\frac{\sqrt{6}(162-165)}{\sqrt{3.665}}=-3.504\in R $$
となるので、帰無仮説 \( H_0 \) は棄却される。
よって、この学校の男子高校生の平均身長は \( 165 \) cmの正規母集団からの標本とみなせないといえる。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

