こんにちは、ひかりです。
今回は確率・統計から二項分布と幾何分布について解説していきます。
この記事では以下のことを紹介します。
- ベルヌーイ分布と二項分布について
- 幾何分布と負の二項分布について
- 多項分布について
ベルヌーイ分布と二項分布
ここから、何回かの記事にわたって統計学でよく用いることとなる代表的な確率分布を紹介していきます。
ベルヌーイ分布
ある試行に対して、特定の事象が起きるか、起きないかということに注目します。
(例えば、さいころを投げて1の目が出るか、出ないか)
このとき、その事象が起きたときに「成功」、起きなかったときに「失敗」というように考えて、この試行を互いに独立に繰り返します。
このような試行のことをベルヌーイ試行または二項試行といいます。
(要するに、高校数学や確率・統計06などで学んできた反復試行のことです)
では、事象 \( A \) が起きる確率が \( p \) のベルヌーイ試行を1回行って、事象 \( A \) が起こる回数を \( X \) とします。
すると、 \( X \) は \( 0 \) か \( 1 \) の値をとる確率変数であり、その確率は
$$ P(X=1)=p, \quad P(X=0)=1-p $$
となります。よって、 \( X \) の確率分布は次のようになります。
| \( X \) | \( 0 \) | \( 1 \) | 計 |
| \( P \) | \( 1-p \) | \( p \) | \( 1 \) |
この確率分布のことをベルヌーイ分布といい、 \( Be(p) \) と表します。
ベルヌーイ分布の期待値と分散は次のようになります。
確率変数 \( X \) がベルヌーイ分布 \( Be(p) \) に従っているとする。このとき、
$$ E(X)=p, \quad V(X)=p(1-p) $$
定理1の証明(気になる方だけクリックしてください)
$$ E(X)=1\times p+0\times (1-p)=p $$
$$ E(X^2)=1^2\times p+0^2\times (1-p)=p $$
$$ V(X)=E(X^2)-\{E(X)\}^2=p-p^2=p(1-p) $$
さいころを1回投げて1の目が出るか、出ないかを考える。
このとき、1の目が出る回数を \( X \) とおくと、 \( X \) はベルヌーイ分布 \( Be(\frac{1}{6}) \) に従う。
よって、
$$ E(X)=\frac{1}{6}, \quad V(X)=\frac{1}{6}\left(1-\frac{1}{6}\right)=\frac{5}{36} $$
二項分布
今度は、事象 \( A \) が起きる確率が \( p \) のベルヌーイ試行を \( n \) 回行って、事象 \( A \) が起こる回数を \( X \) としましょう。
すると、 \( X \) は \( 0 \) から \( n \) までの整数の値をとる確率変数であり、その確率は反復試行の確率なので、
$$ P(X=k)={}_nC_kp^kq^{n-k}, \quad ここで \ q=1-p $$
となります。よって、 \( X \) の確率分布は次のようになります。
| \( X \) | \( 0 \) | \( 1 \) | \( \cdots \) | \( k \) | \( \cdots \) | \( n \) | 計 |
| \( P \) | \( {}_nC_0q^n \) | \( {}_nC_1pq^{n-1} \) | \( \cdots \) | \( {}_nC_kp^kq^{n-k} \) | \( \cdots \) | \( {}_nC_np^n \) | \( 1 \) |
この確率分布のことを二項分布といい、 \( B(n,p) \) と表します。
(つまり、 \( B(1,p) \) がベルヌーイ分布となります)
なぜ二項分布というのかというと、この二項分布の確率が、二項定理
$$ (p+q)^n={}_nC_0q^n+{}_nC_1pq^{n-1}+\cdots+{}_nC_kp^kq^{n-k}+\cdots+{}_nC_np^n $$
の右辺の各項に等しくなるためです。
ここで、 \( p+q=1 \) であるので、左辺に代入すると二項分布の各確率の和は \( 1 \) となります。
(1) 1個のさいころを5回繰り返し投げるとき、1の目が出る回数を \( X \) とすると、 \( X \) は二項分布 \( B(5,\frac{1}{6}) \) に従う。
このとき、 \( X \) の確率分布は次のようになる。(小数第4位で四捨五入)
ただし、 \( X=5 \) の確率は \( 0.00012\cdots \) である。
| \( X \) | \( 0 \) | \( 1 \) | \( 2 \) | \( 3 \) | \( 4 \) | \( 5 \) | 計 |
| \( P \) | \( 0.402 \) | \( 0.402 \) | \( 0.161 \) | \( 0.032 \) | \( 0.003 \) | \( 0.000 \) | \( 1 \) |
また、このとき1の目が出る回数が1回以上3回以下である確率を求めると、
$$ \begin{align} P(1≦X≦3)&=P(X=1)+P(X=2)+P(X=3) \\ &≒0.402+0.161+0.032≒0.595 \end{align} $$
(2) 二項分布 \( B(n,\frac{1}{6}) \) の確率
$$ p_r={}_nC_r\left(\frac{1}{6} \right)^r\left(\frac{5}{6} \right)^{n-r} $$
に関して、 \( r \) を横軸、 \( p_r \) を縦軸にした折れ線グラフを \( n=6,12,30,50 \) について示すと、次のようになる。
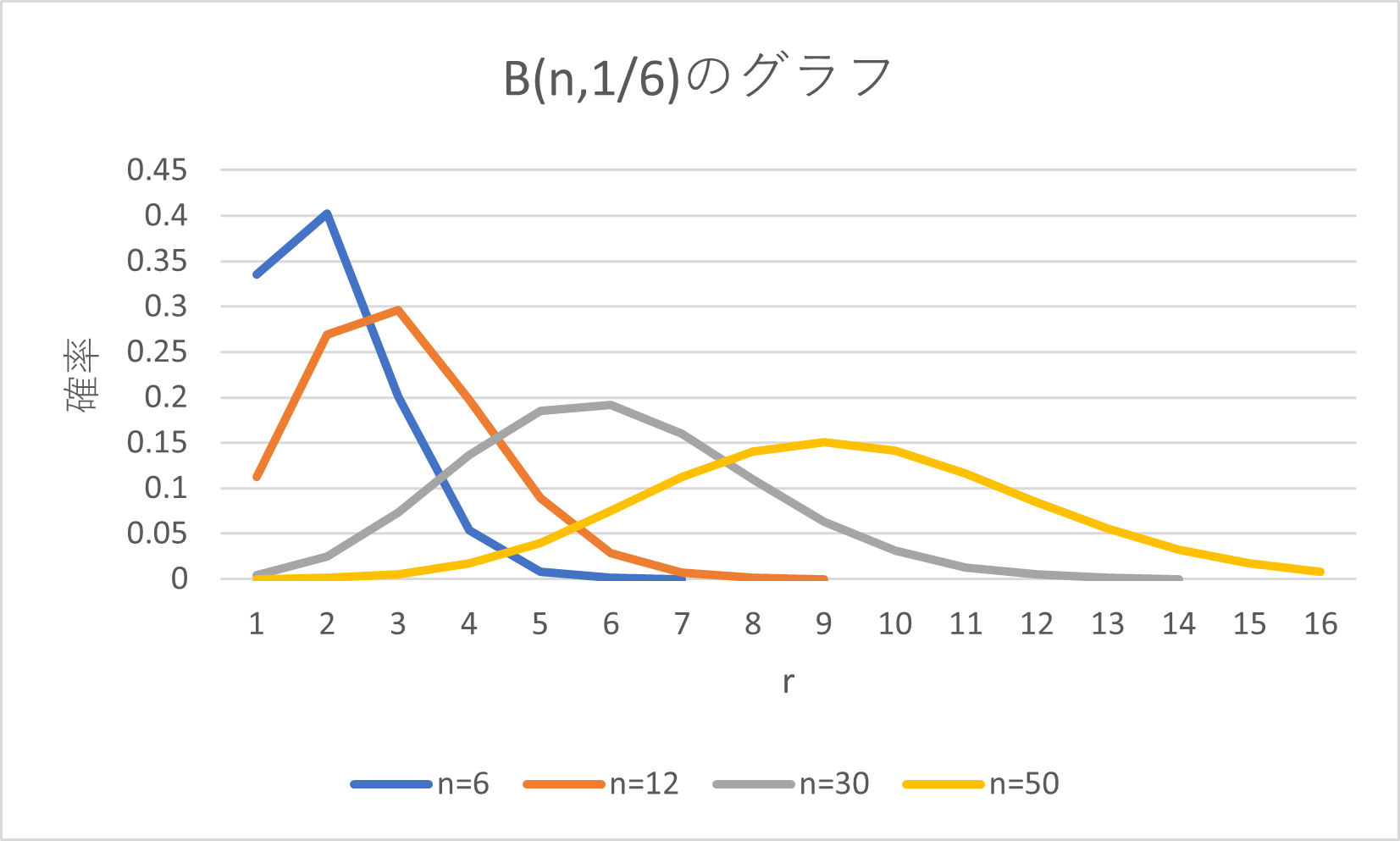
このグラフから、 \( B(n,\frac{1}{6}) \) のグラフは \( n \) が大きくなるにつれて、左右対称な山型の曲線に近づいていくことが分かる。
(これは一般の \( B(n,p) \) でも成り立つ)
二項分布の性質として、次が成り立ちます。
確率変数 \( X \) が二項分布 \( B(n,p) \) に従っているとする。このとき、
(1) $$ E(X)=np, \quad V(X)=np(1-p)=npq $$
(2) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=(q+pe^t)^n $$
(3) (二項分布の再生性) 確率変数 \( Y \) が二項分布 \( B(m,p) \) に従っているとする。
また、 \( X \) と \( Y \) が独立であるとする。
このとき、 \( X+Y \) は二項分布 \( B(n+m,p) \) に従う。
定理2の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} E(X)&=\sum_{k=0}^nk{}_nC_kp^kq^{n-k}=\sum_{k=0}^nk\frac{n!}{k!(n-k)!}p^kq^{n-k} \\ &=np\sum_{k=1}^n\frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1}q^{n-k} \quad (k=0のときは和の中身は0) \\ &=np\sum_{\ell=0}^{n-1}\frac{(n-1)!}{\ell!(n-1-\ell)!}p^{\ell}q^{n-1-\ell} \quad (\ell=k-1とおく) \\ &=np\sum_{\ell=0}^{n-1}{}_{n-1}C_{\ell}p^{\ell}q^{n-1-\ell} \\ &=np(p+q)^{n-1} \quad (二項定理より) \\ &=np \quad (p+q=1より) \end{align} $$
$$ \begin{align} E[X(X-1)]&=\sum_{k=0}^nk(k-1){}_nC_kp^kq^{n-k} \\ &=\sum_{k=0}^nk(k-1)\frac{n!}{k!(n-k)!}p^kq^{n-k} \\ &=n(n-1)p^2\sum_{k=2}^n\frac{(n-2)!}{(k-2)!(n-k)!}p^{k-2}q^{n-k} \quad (k=0,1のときは和の中身は0) \\ &=n(n-1)p^2\sum_{\ell=0}^{n-2}\frac{(n-2)!}{\ell!(n-2-\ell)!}p^{\ell}q^{n-2-\ell} \quad (\ell=k-2とおく) \\ &=n(n-1)p^2\sum_{\ell=0}^{n-2}{}_{n-2}C_{\ell}p^{\ell}q^{n-2-\ell} \\ &=n(n-1)p^2(p+q)^{n-2} \quad (二項定理より) \\ &=n(n-1)p^2 \quad (p+q=1より) \end{align} $$
より、
$$ \begin{align} V(X)&=E(X^2)-\{ E(X) \}^2=E[X(X-1)]+E(X)-\{ E(X) \}^2 \\ &=n(n-1)p^2+np-n^2p^2 \\ &=np(1-p)=npq \end{align} $$
(2) 二項定理より、
$$ \begin{align} M_X(t)&=E(e^{tX})=\sum_{k=0}^ne^{tk}{}_nC_kp^kq^{n-k} \\ &=\sum_{k=0}^n{}_nC_k(pe^t)^kq^{n-k}=(q+pe^t)^n \end{align} $$
(3) \( X \) のモーメント母関数は \( (q+pe^t)^n \) 、 \( Y \) のモーメント母関数は \( (q+pe^t)^m \) である。
このとき、 \( X+Y \) のモーメント母関数は \( X \) と \( Y \) は独立であるので、確率・統計09の定理3のあとの注意より、
$$ \begin{align} M_{X+Y}(t)&=E(e^{X+Y})=E(e^Xe^Y) \\ &=E(e^X)E(e^Y) \quad (XとYは独立であることより) \\ &=(q+pe^t)^n(q+pe^t)^m=(q+pe^t)^{n+m} \end{align} $$
したがって、 \( X+Y \) は \( B(n+m,p) \) に従う。
ある宝くじで10万円が当たる確率が \( 0.02 \) であるとする。
100本の宝くじがあるとき、当たりの本数 \( X \) の平均と標準偏差を求める。
\( X \) は二項分布 \( B(100,0.02) \) に従う。
したがって、 \( X \) の平均と標準偏差は
$$ E(X)=100\times 0.02=2 $$
$$ \sigma(X)=\sqrt{V(X)}=\sqrt{100\times 0.02 \times 0.98}=\sqrt{1.96}=1.4 $$
幾何分布と負の二項分布
幾何分布
二項分布では、ベルヌーイ試行の回数を \( n \) 回で固定していましたが、今度はベルヌーイ試行で初めて成功するまで何回も試行を続けるものとします。
このとき、初めて成功するまでの試行回数を \( X \) とします。
すると、 \( X \) は正の整数の値をとる確率変数であり、 \( X=k \) となるのは \( k-1 \) 回失敗が続いた後、 \( k \) 回目に成功するときであるので、
$$ P(X=k)=q^{k-1}p, \quad (k=1,2,\cdots) $$
となります。よって、 \( X \) の確率分布は次のようになります。
| \( X \) | \( 1 \) | \( \cdots \) | \( k \) | \( \cdots \) | 計 |
| \( P \) | \( p \) | \( \cdots \) | \( q^{k-1}p \) | \( \cdots \) | \( 1 \) |
この確率分布のことを幾何分布といい、 \( Ge(p) \) と表します。
なぜ幾何分布というのかというと、幾何分布の各確率の和を計算してみると、
$$ \sum_{k=1}^{\infty}P(X=k)=\sum_{k=1}^{\infty}q^{k-1}p=\frac{p}{1-q}=1 $$
となり、無限等比級数が出てきます。
等比級数は幾何級数ともよばれていることから、この名前が付けられました。
さいころを1の目が出るまで投げ続けるとき、3回以内で初めて1の目が出る確率を求める。
初めて1の目が出るまでに投げた回数を \( X \) とすると、 \( X \) は幾何分布 \( Ge(\frac{1}{6}) \) に従う。
よって、求める確率は
$$ \begin{align} \sum_{k=1}^3P(X=k)&=\sum_{k=1}^3\left(\frac{5}{6} \right)^{k-1}\cdot \frac{1}{6} \\ &=\frac{1}{6}+\frac{5}{6} \cdot \frac{1}{6}+\left(\frac{5}{6} \right)^{2}\cdot \frac{1}{6}=\frac{91}{216} \end{align} $$
幾何分布の性質として、次が成り立ちます。
確率変数 \( X \) が幾何分布 \( Ge(p) \) に従っているとする。このとき、
(1) $$ E(X)=\frac{1}{p}, \quad V(X)=\frac{1-p}{p^2}=\frac{q}{p^2} $$
(2) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=\frac{pe^t}{1-qe^t} $$
(3) (幾何分布の無記憶性)
$$ P(X=n+j \ | \ X>n)=P(X=j) \quad (j=1,2,\cdots) $$
(つまり、 \( j \) 回目に初めて成功する確率と \( n \) 回失敗した後にさらに \( j \) 回試行したときに初めて成功する確率は同じということであり、幾何分布は \( n \) 回失敗したということを記憶していない)
定理3の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} E(X)&=\sum_{k=1}^{\infty}kq^{k-1}p=p\sum_{k=1}^{\infty}kq^{k-1} \\ &=p\sum_{k=1}^{\infty}\frac{d}{dq}(q^k) \\ &=p\frac{d}{dq}\sum_{k=1}^{\infty}q^k \quad (0<q<1より微分と無限和の交換可能) \\ &=p\frac{d}{dq}\left(\frac{q}{1-q} \right)=p\cdot \frac{1}{(1-q)^2}=\frac{1}{p} \end{align} $$
また、
$$ \begin{align} E[X(X-1)]&=\sum_{k=1}^{\infty}k(k-1)q^{k-1}p \\ &=pq\sum_{k=2}^{\infty}k(k-1)q^{k-2} \quad (k=1のとき和の中身は0) \\ &=pq\sum_{k=2}^{\infty}\frac{d^2}{dq^2}(q^k) \\ &=pq\frac{d^2}{dq^2}\sum_{k=2}^{\infty}q^k \quad (0<q<1より微分と無限和の交換可能) \\ &=pq\frac{d^2}{dq^2}\left(\frac{q^2}{1-q} \right)=pq\cdot \frac{2}{(1-q)^3}=\frac{2q}{p^2} \end{align} $$
より、
$$ \begin{align} V(X)&=E(X^2)-\{E(X)\}^2=E[X(X-1)]+E(X)-\{E(X)\}^2 \\ &=\frac{2q}{p^2}+\frac{1}{p}-\frac{1}{p^2}=\frac{1}{p^2}(2q+p-1)=\frac{q}{p^2} \end{align} $$
(2) $$ \begin{align} M_X(t)&=E(e^{tX})=\sum_{k=1}^{\infty}e^{tk}q^{k-1}p=\frac{p}{q}\sum_{k=1}^{\infty}(qe^t)^k \\ &=\frac{p}{q}\left(\frac{qe^t}{1-qe^t} \right)=\frac{pe^t}{1-qe^t} \end{align} $$
(3) 条件付き確率の定義より、
$$ \begin{align} P(X=n+j \ | \ X>n)&=\frac{P(X=n+j, X>n)}{P(X>n)} \\ &=\frac{P(X=n+j)}{P(X>n)} \quad (X=n+jであればX>nなのは当然) \\ &=\frac{q^{n+j-1}p}{\displaystyle \sum_{k=n+1}^{\infty}q^{k-1}p}=\frac{q^{n+j-1}p}{\displaystyle \frac{q^np}{1-q}}=q^{j-1}p=P(X=j) \end{align} $$
さいころを1の目が出るまで投げ続けるとき、初めて1の目が出るまでに投げた回数 \( X \) の期待値と標準偏差を求める。
\( X \) は幾何分布 \( Ge(\frac{1}{6}) \) に従うので、
$$ E(X)=\frac{1}{\frac{1}{6}}=6 $$
$$ \sigma(X)=\sqrt{V(X)}=\sqrt{\frac{\frac{5}{6}}{\frac{1}{36}}}=\sqrt{30}=5.48 $$
負の二項分布
幾何分布の一般化について考えてみましょう。
ベルヌーイ試行において \( r \) 回成功するまでの失敗の回数を \( X \) とします。
すると、 \( X \) は0以上の整数の値をとる確率変数であり、 \( X=k \) となるのはベルヌーイ試行を \( k+r \) 回繰り返したときに \( k+r \) 回目に \( r \) 回目の成功が起きることであるので、
$$ P(X=k)={}_{k+r-1}C_kp^{r-1}q^k\times p={}_{k+r-1}C_kp^rq^k, \quad (k=0,1,2,\cdots) $$
となります。よって、 \( X \) の確率分布は次のようになります。
| \( X \) | \( 0 \) | \( \cdots \) | \( k \) | \( \cdots \) | 計 |
| \( P \) | \( p^r \) | \( \cdots \) | \( {}_{k+r-1}C_kp^rq^k \) | \( \cdots \) | \( 1 \) |
この確率分布のことを負の二項分布といい、 \( NB(r,p) \) と表します。
(つまり、 \( NB(1,p) \) が(例4の前の注意で述べた方の)幾何分布となります)
なぜ負の二項分布というのかというと、負の二項分布の各確率の和を計算する際に負の二項定理
$$ (1-q)^{-r}=\sum_{k=0}^{\infty}{}_{-r}C_k(-q)^k $$
を用いているためです。
実際に、負の二項分布の各確率の和を計算します。
$$ \begin{align} \frac{1}{p^r}&=\{ 1-(1-p) \}^{-r}=(1-q)^{-r}=\sum_{k=0}^{\infty}{}_{-r}C_k(-q)^k \\ &=\sum_{k=0}^{\infty}{}_{k+r-1}C_{r-1}q^k=\sum_{k=0}^{\infty}{}_{k+r-1}C_{k}q^k \end{align} $$
と変形をして、最両辺に \( p^r \) をかけると、
$$ \sum_{k=0}^{\infty}{}_{k+r-1}C_kp^rq^k=1 $$
となり、負の二項分布の各確率の和は1となります。
さいころを1の目が3回出るまで投げ続けるとき、1の目が出なかった回数 \( X \) が7回である確率を求める。
\( X \) は負の二項分布 \( NB(3,\frac{1}{6}) \) に従うので、
$$ P(X=7)={}_{9}C_7\left(\frac{1}{6} \right)^3\left( \frac{5}{6} \right)^7=\frac{1}{6}\left( \frac{5}{6} \right)^7≒0.047 $$
負の二項分布の性質として、次が成り立ちます。
確率変数 \( X \) が負の二項分布 \( NB(r,p) \) に従っているとする。このとき、
(1) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=\left(\frac{p}{1-qe^t}\right)^r $$
(2) $$ E(X)=\frac{rq}{p}, \quad V(X)=\frac{rq}{p^2} $$
(3) (負の二項分布の再生性) 確率変数 \( Y \) が負の二項分布 \( NB(s,p) \) に従っているとする。
また、 \( X \) と \( Y \) が独立であるとする。
このとき、 \( X+Y \) は負の二項分布 \( NB(r+s,p) \) に従う。
定理4の証明(気になる方だけクリックしてください)
(1) 負の二項定理
$$ (1-q)^{-r}=\sum_{k=0}^{\infty}{}_{-r}C_k(-q)^k=\sum_{k=0}^{\infty}{}_{k+r-1}C_kq^k $$
を用いることにより、
$$ \begin{align} M_X(t)&=E(e^{tX})=\sum_{k=0}^{\infty}e^{tk}{}_{k+r-1}C_kp^rq^k \\ &=p^r\sum_{k=0}^{\infty}{}_{k+r-1}C_k(qe^t)^k=p^r(1-qe^t)^{-r}=\left(\frac{p}{1-qe^t}\right)^r \end{align} $$
(2) (1)のモーメント母関数 \( M_X(t) \) を微分すると、
$$ \begin{align} M_X'(t)&=\frac{d}{dt}\left(\frac{p}{1-qe^t}\right)^r=\frac{-p^r\{(1-qe^t)^r\}’}{(1-qe^t)^{2r}} \\ &=\frac{-rp^r(1-qe^t)^{r-1}(-qe^t)}{(1-qe^t)^{2r}} \\ &=\frac{rp^rqe^t(1-qe^t)^{r-1}}{(1-qe^t)^{2r}}=\frac{rp^rqe^t}{(1-qe^t)^{r+1}} \end{align} $$
$$ \begin{align} M_X^{\prime\prime}(t)&=\frac{d}{dt}\left(\frac{rp^rqe^t}{(1-qe^t)^{r+1}}\right) \\ &=\frac{(rp^rqe^t)'(1-qe^t)^{r+1}-(rp^rqe^t)\{(1-qe^t)^{r+1}\}’}{(1-qe^t)^{2r+2}} \\ &=\frac{(rp^rqe^t)(1-qe^t)^{r+1}+(rp^rq^2e^{2t})(r+1)(1-qe^t)^r}{(1-qe^t)^{2r+2}} \\ &=\frac{(rp^rqe^t)(1-qe^t)+(rp^rq^2e^{2t})(r+1)}{(1-qe^t)^{r+2}} \end{align} $$
したがって、
$$ \begin{align} E(X)&=M_X'(0)=\frac{rp^rq}{(1-q)^{r+1}}=\frac{rq}{p} \end{align} $$
$$ \begin{align} E(X^2)&=M_X^{\prime\prime}(0)=\frac{(rp^rq)(1-q)+(rp^rq^2)(r+1)}{(1-q)^{r+2}} \\ &=\frac{rq(1-q)+(rq^2)(r+1)}{p^2} \\ &=\frac{rq-rq^2+r^2q^2+rq^2}{p^2}=\frac{r^2q^2+rq}{p^2} \end{align} $$
$$ \begin{align} V(X)&=E(X^2)-\{ E(X) \}^2=\frac{r^2q^2+rq}{p^2}-\frac{r^2q^2}{p^2}=\frac{rq}{p^2} \end{align} $$
(3) \( X \) のモーメント母関数は \( \left(\frac{p}{1-qe^t}\right)^r \) 、 \( Y \) のモーメント母関数は \( \left(\frac{p}{1-qe^t}\right)^s \) である。
このとき、 \( X+Y \) のモーメント母関数は \( X \) と \( Y \) は独立であるので、確率・統計09の定理3のあとの注意より、
$$ \begin{align} M_{X+Y}(t)&=E(e^{X+Y})=E(e^Xe^Y) \\ &=E(e^X)E(e^Y) \quad (XとYは独立であることより) \\ &=\left(\frac{p}{1-qe^t}\right)^r\left(\frac{p}{1-qe^t}\right)^s=\left(\frac{p}{1-qe^t}\right)^{r+s} \end{align} $$
したがって、 \( X+Y \) は \( NB(r+s,p) \) に従う。
さいころを1の目が3回出るまで投げ続けるとき、1の目が出なかった回数 \( X \) の期待値と標準偏差を求める。
\( X \) は負の二項分布 \( NB(3,\frac{1}{6}) \) に従うので、
$$ E(X)=\frac{3\times \frac{5}{6}}{\frac{1}{6}}=15 $$
$$ \sigma(X)=\sqrt{V(X)}=\sqrt{\frac{3\times \frac{5}{6}}{\frac{1}{36}}}=\sqrt{90}=3\sqrt{10}≒9.487 $$
多項分布
二項分布の一般化について考えてみましょう。
ベルヌーイ試行では成功か失敗かの2択でしたが、今度は1回の試行で事象 \( A_1,A_2,\cdots,A_k \) のうちどれか1つだけが起きるとします。
ただし、 \( A_1,A_2,\cdots,A_k \) は互いに排反な事象として、それらが起きる確率を \( P(A_i)=p_i \) とします。
このとき、もちろん
$$ p_i≧0, \quad p_1+p_2+\cdots+p_k=1 $$
この試行を独立に \( n \) 回くり返して、各事象 \( A_i \) が起きた回数をそれぞれ \( X_i \ (i=1,2,\cdots,k) \) とします。
つまり、
$$ X_1+X_2+\cdots+X_k=n $$
このとき、 \( n=n_1+n_2+\cdots+n_k \) となる非負の整数の組 \( (n_1,n_2,\cdots,n_k) \) に対して、確率
$$ P(X_1=n_1,X_2=n_2,\cdots,X_k=n_k) $$
を求めたい。これは \( A_1,A_2,\cdots,A_k \) と書かれた \( k \) 個の球を1回1回球を戻しながら \( n \) 回引いたときに、各 \( i \) に対して球 \( A_i \) が \( n_i \) 回出る確率と考えられるので、
$$ P(X_1=n_1,X_2=n_2,\cdots,X_k=n_k)=\frac{n!}{n_1!n_2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k} $$
となります。
このとき、確率変数 \( X=(X_1,X_2,\cdots,X_k) \) がみたす確率分布のことを多項分布といい、 \( Mult(n,p_1,p_2,\cdots,p_k) \) と表します。
(つまり \( k=2 \) である \( Mult(n,p,q) \) が二項分布となります。)
なぜ多項分布というのかというと、この多項分布の確率が、多項定理
$$ (p_1+p_2+\cdots+p_k)^n=\sum \frac{n!}{n_1!n_2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k} $$
(ここで、 \( \sum \) は \( n=n_1+n_2+\cdots+n_k \) となるすべての非負の整数の組 \( (n_1,n_2,\cdots,n_k) \) に対する和を表します。)
の右辺の各項に等しくなるためです。
ここで、 \( p_1+p_2+\cdots+p_k=1 \) であるので、左辺に代入すると多項分布の各確率の和は \( 1 \) となります。
さいころを10回投げたとき、1の目が3回、4の目が2回、それ以外の目が5回でる確率を求める。
1の目が出る回数を \( X_1 \) 、4の目が出る回数を \( X_2 \) 、それ以外の目が出る回数を \( X_3 \) とおくと、 \( X=(X_1,X_2,X_3) \) は多項分布 \( Mult(10,\frac{1}{6},\frac{1}{6},\frac{2}{3}) \) に従う。
よって、求める確率は
$$ \begin{align} P(X_1=3,X_2=2,X_3=5)&=\frac{10!}{3!2!5!}\left(\frac{1}{6}\right)^3\left(\frac{1}{6} \right)^2\left(\frac{2}{3}\right)^5 \\ &=\frac{2^3\times 5\times 7}{3^8}≒0.043 \end{align} $$
多項分布の性質として、次が成り立ちます。
確率変数 \( X=(X_1,X_2,\cdots,X_k) \) が多項分布 \( Mult(n,p_1,p_2,\cdots,p_k) \) に従っているとする。このとき、
(1) $$ E(X_i)=np_i, \quad V(X_i)=np_i(1-p_i) \quad (i=1,2,\cdots,k) $$
(2) \( X_i \) と \( X_j \) の共分散は
$$ \text{Cov}(X_i,X_j)=-np_ip_j, \quad (i\not=j) $$
定理5の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} E(X_i)&=\sum_{n_i=0}^nn_i\frac{n!}{n_1!n_2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k} \\ &=\sum_{n_i=1}^nn_i\frac{n!}{n_1!n_2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k} \quad (n_i=0のとき和の中身は0) \\ &=\sum_{n_i=1}^n\frac{n\cdot (n-1)!}{n_1!n_2!\cdots(n_i-1)!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_i^{n_i}\cdots p_k^{n_k} \\ &=np_i\sum_{n_i=1}^n\frac{(n-1)!}{n_1!n_2!\cdots(n_i-1)!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_i^{n_i-1}\cdots p_k^{n_k} \\ &=np_i \quad (最後の和は多項分布の周辺分布の和なので1) \end{align} $$
また、
$$ \begin{align} E[X_i(X_i-1)]&=\sum_{n_i=0}^nn_i(n_i-1)\frac{n!}{n_1!n_2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k} \\ &=\sum_{n_i=2}^nn_i(n_i-1)\frac{n!}{n_1!n_2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k} \quad (n_i=0,1のとき和の中身は0) \\ &=\sum_{n_i=2}^n\frac{n(n-1)\cdot (n-2)!}{n_1!n_2!\cdots(n_i-2)!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_i^{n_i}\cdots p_k^{n_k} \\ &=n(n-1)p_i^2\sum_{n_i=2}^n\frac{(n-2)!}{n_1!n_2!\cdots(n_i-2)!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_i^{n_i-2}\cdots p_k^{n_k} \\ &=n(n-1)p_i^2 \quad (最後の和は多項分布の周辺分布の和なので1) \end{align} $$
より、
$$ \begin{align} V(X_i)&=E(X^2_i)-\{E(X_i)\}^2=E[X_i(X_i-1)]+E(X_i)-\{E(X_i)\}^2 \\ &=n(n-1)p_i^2+np_i-n^2p_i^2=np_i(1-p_i) \end{align} $$
(2) \( i<j \) とします。 \( i>j \) でも同様に示せます。
$$ \begin{align} &E(X_iX_j) \\ &=\sum_{\substack{n_i,n_j=0 \\ n=n_i+n_j}}^nn_in_j\frac{n!}{n_1!n_2!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_k^{n_k} \\ &=\sum_{\substack{n_i,n_j=1 \\ n=n_i+n_j}}^{n-1}\frac{n(n-1)\cdot (n-2)!}{n_1!n_2!\cdots(n_i-1)!\cdots (n_j-1)!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_i^{n_i}\cdots p_j^{n_j}\cdots p_k^{n_k} \\ &=n(n-1)p_ip_j\sum_{\substack{n_i,n_j=1 \\ n=n_i+n_j}}^{n-1}\frac{(n-2)!}{n_1!n_2!\cdots(n_i-1)!\cdots (n_j-1)!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_i^{n_i-1}\cdots p_j^{n_j-1}\cdots p_k^{n_k} \\ &=n(n-1)p_ip_j\sum_{\substack{n’_i,n’_j=0 \\ n-2=n’_i+n’_j}}^{n-2}\frac{(n-2)!}{n_1!n_2!\cdots n’_i!\cdots n’_j!\cdots n_k!}p_1^{n_1}p_2^{n_2}\cdots p_i^{n’_i}\cdots p_j^{n’_j}\cdots p_k^{n_k} \\ &=n(n-1)p_ip_j \quad (最後の和は多項分布の周辺分布の和なので1) \end{align} $$
より、
$$ \begin{align} \text{Cov}(X_i,X_j)&=E(X_iX_j)-E(X_i)E(X_j) \\ &=n(n-1)p_ip_j-n^2p_ip_j=-np_ip_j \end{align} $$
さいころを10回投げたとき、1の目が出る回数を \( X_1 \) 、4の目が出る回数を \( X_2 \) 、それ以外の目が出る回数を \( X_3 \) の平均と分散とそれぞれの共分散を求める。
\( X=(X_1,X_2,X_3) \) は多項分布 \( Mult(10,\frac{1}{6},\frac{1}{6},\frac{2}{3}) \) に従うので、
$$ E(X_1)=\frac{5}{3}, \quad E(X_2)=\frac{5}{3}, \quad E(X_3)=\frac{20}{3} $$
$$ V(X_1)=\frac{25}{18}, \quad V(X_2)=\frac{25}{18}, \quad V(X_3)=\frac{20}{9} $$
$$ \text{Cov}(X_1,X_2)=-\frac{5}{18}, \quad \text{Cov}(X_1,X_3)=-\frac{10}{9}, \quad \text{Cov}(X_2,X_3)=-\frac{10}{9} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

