こんにちは、ひかりです。
今回は確率・統計から期待値・分散とモーメント(積率)について解説していきます。
この記事では以下のことを紹介します。
- 期待値と分散について
- 歪度と尖度について
- モーメントとモーメント母関数について
期待値と分散
期待値
まず、次の例を考えてみましょう。
1等が100本、2等が200本、3等が300本、はずれが400本のくじがある。
1等は500円、2等は300円、3等は200円、はずれは0円もらえるとする。
このとき、1本のくじを引くときの賞金の平均は、賞金の総額をくじの本数で割ったものであるので、
$$ \frac{500\times100+300\times 200+200\times 300+0\times 400}{1000}=\frac{170000}{1000}=170 \ (円) $$
これは次のように考えることができる。
$$ 500\times\frac{100}{1000}+300\times \frac{200}{1000}+200\times \frac{300}{1000}+0\times\frac{400}{1000}=170 \ (円) $$
そこで、くじを引いたときに得られる賞金を \( X \) とおくと、
$$ 500\times P(X=500)+300\times P(X=300)+200\times P(X=200)+0\times P(X=0)=170 \ (円) $$
となり、くじを1回引いたときに期待できる賞金の額というふうにも考えられる。
これをもとに有限個の値をとる確率変数の期待値を次のように定義します。
確率変数 \( X \) のとる値が \( x_1,x_2,\cdots,x_n \) で、 \( X \) がそれぞれの値をとる確率が \( p_1,p_2,\cdots,p_n \) であるとき、確率変数 \( X \) の期待値もしくは平均 \( E(X) \) を次で定める。
$$ E(X)=x_1p_1+x_2p_2+\cdots +x_np_n $$
さらに、もっと一般に確率変数 \( X \) の期待値を次で定めます。
確率変数 \( X \) に対して、 \( X \) の期待値もしくは平均 \( E(X) \) を次で定める。
$$ E(X)=\begin{cases} \displaystyle \sum_{i=1}^{\infty}x_ip_i & (Xが離散型確率変数) \\ \displaystyle \int_{-\infty}^{\infty}xf(x)dx & (Xが連続型確率変数) \end{cases} $$
(1) 確率・統計07の例5の確率変数 \( X \) とその確率関数
$$ p(k)=P(X=k)=\frac{1}{k!}e^{-1} \quad (k=0,1,2,\cdots) $$
を考える。このとき、期待値 \( E(X) \) を求める。
\( e^x \) のマクローリン展開を思い出すと、
$$ \begin{align} E(X)&=\sum_{k=0}^{\infty}k\frac{1}{k!}e^{-1} \quad (k=0に注意) \\ &=\sum_{k=1}^{\infty}k\frac{1}{k!}e^{-1} \quad (k=0のときk\frac{1}{k!}e^{-1}=0) \\ &=\sum_{k=1}^{\infty}\frac{1}{(k-1)!}e^{-1}=ee^{-1} \quad (e^1のマクローリン展開) \\ &=1 \end{align} $$
(2) 確率・統計07の例6の確率変数 \( X \) とその確率密度関数
$$ f(x)=\begin{cases} \frac{1}{b-a} & (x\in [a,b]) \\ 0 & (それ以外) \end{cases} $$
を考える。このとき、期待値 \( E(X) \) を求める。
$$ \begin{align} E(X)&=\int_{-\infty}^{\infty}xf(x)dx=\int_a^bx\frac{1}{b-a}dx \quad (x\not\in[a,b]ではf(x)=0) \\ &=\frac{1}{b-a}\left[ \frac{1}{2}x^2 \right]_a^b=\frac{b^2-a^2}{2(b-a)}=\frac{a+b}{2} \end{align} $$
また、確率変数 \( X \) と連続関数 \( g(x) \) に対して、 \( g(X) \) を考えるとこれも確率変数となることが知られています。
(例えば、確率変数 \( X \) に対して \( X^2 \) や \( \log X \) も確率変数になります)
この確率変数 \( g(X) \) に対しても期待値 \( E(g(X)) \) を次のように定めます。
確率変数 \( X \) と連続関数 \( g(x) \) に対して、確率変数 \( g(X) \) の期待値もしくは平均 \( E(g(X)) \) を次で定める。
$$ E(g(X))=\begin{cases} \displaystyle \sum_{i=1}^{\infty}g(x_i)p_i & (Xが離散型確率変数) \\ \displaystyle \int_{-\infty}^{\infty}g(x)f(x)dx & (Xが連続型確率変数) \end{cases} $$
コインを3回投げたときに表が出た回数を \( X \) とする。
まず、 \( X \) の確率分布を求めておくと、
| \( X \) | \( 0 \) | \( 1 \) | \( 2 \) | \( 3 \) | 計 |
| \( P \) | \( \frac{1}{8} \) | \( \frac{3}{8} \) | \( \frac{3}{8} \) | \( \frac{1}{8} \) | \( 1 \) |
このとき、いろいろな確率変数の期待値を求めると、
$$ E(X)=0\times \frac{1}{8}+1\times \frac{3}{8}+2\times \frac{3}{8}+3\times \frac{1}{8}=\frac{3}{2} $$
$$ E(X^2)=0^2\times \frac{1}{8}+1^2\times \frac{3}{8}+2^2\times\frac{3}{8}+3^2\times \frac{1}{8}=3 $$
$$ E(2^X)=2^0\times \frac{1}{8}+2^1\times \frac{3}{8}+2^2\times \frac{3}{8}+2^3\times \frac{1}{8}=\frac{27}{8} $$
$$ E(e^X)=e^0\times \frac{1}{8}+e^1\times \frac{3}{8}+e^2\times \frac{3}{8}+e^3\times \frac{1}{8}=\frac{1}{8}(1+3e+3e^2+e^3) $$
期待値の性質として次が成り立ちます。
確率変数 \( X \) と定数 \( c \) に対して、次が成り立つ。
(1) \( E(c)=c \)
(2) \( E(X+c)=E(X)+c \)
(3) \( E(cX)=cE(X) \)
定理1の証明(気になる方だけクリックしてください)
\( X \) が連続型確率変数のとき示します。離散型確率変数の場合も同様に示せます。
(1) 確率密度関数 \( f(x) \) は \( -\infty \) から \( \infty \) まで積分すると1になることに注意すると、
$$ E(c)=\int_{-\infty}^{\infty}cf(x)dx=c\int_{-\infty}^{\infty}f(x)dx=c $$
(2) 定積分の線形性より、
$$ \begin{align} E(X+c)&=\int_{-\infty}^{\infty}(x+c)f(x)dx=\int_{-\infty}^{\infty}xf(x)dx+c\int_{-\infty}^{\infty}f(x)dx \\ &=E(X)+c \end{align} $$
(3) $$ E(cX)=\int_{-\infty}^{\infty}(cx)f(x)dx=c\int_{-\infty}^{\infty}xf(x)dx=cE(X) $$
例3の確率変数 \( X \) を考えると、
$$ E(3X+2)=3E(X)+2=3\times \frac{3}{2}+2=\frac{13}{2} $$
分散と標準偏差
確率・統計01の記事で、 \( n \) 個のデータ \( x_1,x_2,\cdots,x_n \) に対して平均 \( \bar{x} \) と分散 \( s^2 \) を次で定めました。
$$ \bar{x}=\frac{1}{n}(x_1+x_2+\cdots+x_n)=\frac{1}{n}\sum_{i=1}^nx_i $$
$$ s^2=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2 $$
これを見ると、分散 \( s^2 \) は \( (x_i-\bar{x})^2 \) の平均と考えることができます。
同様にして、確率変数 \( X \) の分散 \( V(X) \) を次で定めます。
確率変数 \( X \) に対して \( X \) の平均を \( \mu \) とおくとき、 \( X \) の分散 \( V(X) \) を次で定める。
$$ \begin{align} V(X)&=E[(X-\mu)^2] \\ &=\begin{cases} \displaystyle \sum_{i=1}^{\infty}(x_i-\mu)^2p_i & (Xが離散型確率変数) \\ \displaystyle \int_{-\infty}^{\infty}(x-\mu)^2f(x)dx & (Xが連続型確率変数) \end{cases} \end{align} $$
また、分散の正の平方根 \( \sqrt{V(X)} \) を標準偏差といい、 \( \sigma(X) \) または単に \( \sigma \) で表す。
(このとき、分散の値は \( \sigma^2 \) となる。)
この定義のままだと計算が大変なので変形をします。
$$ V(X)=E(X^2)-\{E(X)\}^2 $$
定理2の証明(気になる方だけクリックしてください)
$$ \begin{align} V(X)&=E[\{ X-E(X) \}^2] \quad (分散の定義より) \\ &=E[X^2-2XE(X)+\{ E(X) \}^2 ] \\ &=E(X^2)-2E(X)E(X)+\{E(X)\}^2 \quad (E(X)は定数であることに注意して定理1) \\ &=E(X^2)-\{E(X)\}^2 \end{align} $$
(1) 例2(1)の確率変数 \( X \) とその確率関数
$$ p(k)=P(X=k)=\frac{1}{k!}e^{-1} \quad (k=0,1,2,\cdots) $$
を考える。このとき、分散 \( V(X) \) を求める。
例2(1)より、
$$ \{ E(X) \}^2=1^2=1 $$
また、\( e^x \) のマクローリン展開を思い出すと、
$$ \begin{align} E(X^2)&=E(X(X-1))+E(X) \quad (X^2=X(X-1)+Xと分けて定理1) \\ &=\sum_{k=0}^{\infty}k(k-1)\frac{1}{k!}e^{-1}+1 \quad (k=0に注意) \\ &=\sum_{k=2}^{\infty}k(k-1)\frac{1}{k!}e^{-1}+1 \quad (k=0,1のときk(k-1)\frac{1}{k!}e^{-1}=0) \\ &=\sum_{k=2}^{\infty}\frac{1}{(k-2)!}e^{-1}+1=ee^{-1}+1 \quad (e^1のマクローリン展開) \\ &=2 \end{align} $$
したがって、定理2より、
$$ V(X)=E(X^2)-\{E(X)\}^2=2-1=1 $$
(2) 例2(2)の確率変数 \( X \) とその確率密度関数
$$ f(x)=\begin{cases} \frac{1}{b-a} & (x\in [a,b]) \\ 0 & (それ以外) \end{cases} $$
を考える。このとき、分散 \( V(X) \) を求める。
例2(2)より、
$$ \{ E(X) \}^2=\left( \frac{a+b}{2} \right)^2=\frac{(a+b)^2}{4} $$
また、
$$ \begin{align} E(X^2)&=\int_{-\infty}^{\infty}x^2f(x)dx=\int_a^bx^2\frac{1}{b-a}dx \quad (x\not\in[a,b]ではf(x)=0) \\ &=\frac{1}{b-a}\left[ \frac{1}{3}x^3 \right]_a^b=\frac{b^3-a^3}{3(b-a)}=\frac{b^2+ab+a^2}{3} \end{align} $$
したがって、定理2より、
$$ V(X)=E(X^2)-\{E(X)\}^2=\frac{b^2+ab+a^2}{3}-\frac{(a+b)^2}{4}=\frac{(b-a)^2}{12} $$
分散の性質として次が成り立ちます。
確率変数 \( X \) と定数 \( c \) に対して、次が成り立つ。
(1) \( V(c)=0 \)
(2) \( V(X+c)=V(X) \)
(3) \( V(cX)=c^2V(X) \)
定理3の証明(気になる方だけクリックしてください)
(1) \( c \) は定数に注意すると、定理2より、
$$ V(c)=E(c^2)-\{ E(c) \}^2=c^2-c^2=0 $$
(2) $$ \begin{align} V(X+c)&=E[(X+c)^2]-\{ E(X+c) \}^2=E[X^2+2cX+c^2]-\{ E(x)+c \}^2 \\ &=E(X^2)+2cE(X)+c^2-(\{ E(X)\}^2+2cE(X)+c^2) \\ &=E(X^2)-\{ E(X) \}^2=V(X) \end{align} $$
(3) $$ \begin{align} V(cX)&=E[(cX)^2]-\{ E(cX) \}^2=E(c^2X^2)-\{ cE(X) \}^2 \\ &=c^2E(X^2)-c^2\{ E(X) \}^2=c^2(E(X^2)-\{ E(X) \}^2 ) \\ &=c^2V(X) \end{align} $$
確率変数 \( X \) の期待値を \( \mu \) 、標準偏差を \( \sigma \) とするとき、確率変数 \( Z=\frac{X-\mu}{\sigma} \) の期待値と標準偏差を求める。
\( Z=\frac{X}{\sigma}-\frac{\mu}{\sigma} \) より、
$$ E(Z)=\frac{1}{\sigma}E(X)-\frac{\mu}{\sigma}=\frac{\mu}{\sigma}-\frac{\mu}{\sigma}=0 $$
$$ V(Z)=\frac{1}{\sigma^2}V(X)=\frac{\sigma^2}{\sigma^2}=1 $$
$$ \sigma(Z)=\sqrt{V(Z)}=1 $$
このように、確率変数 \( X \) に対して、 \( Z=\frac{X-\mu}{\sigma} \) という変換をおこなうことにより、平均 \( 0 \) 、分散 \( 1 \) とすることができる。
この変換を確率変数の標準化といい、 \( Z \) を標準化変数という。
歪度と尖度
確率変数 \( X \) に対して、 \( X \) の1乗を考えることにより、 \( X \) の期待値が求められました。
これは確率分布の中心の位置を表す指標となります。
また、 \( X \) の2乗までを考えることにより、 \( X \) の分散が求められました。
これは確率分布の散らばり具合を表す指標となります。
では、 \( X \) の3乗や4乗まで考えたら、何が得られるのでしょうか。
歪度
確率変数 \( X \) の確率分布の歪度(わいど)を次で定めます。
確率変数 \( X \) に対して、平均を \( \mu \) 、標準偏差を \( \sigma \) とおく。
このとき、 \( X \) の確率分布の歪度 \( \alpha_3 \) を次で定める。
$$ \alpha_3=\frac{E[(X-\mu)^3]}{\sigma^3} $$
これは、確率分布の対称性を表す指標となっていて、 \( \alpha_3>0 \) のときは右の裾が長い確率分布、 \( \alpha_3<0 \) のときは左の裾が長い確率分布となります。
また、歪度は定義通りに計算するのは大変なので、分子を変形をすると、
$$ \begin{align} E[(X-\mu)^3]&=E[X^3-3\mu X^2+3\mu^2 X-\mu^3] \\ &=E(X^3)-3\mu E(X^2)+3\mu^2E(X)-\mu^3 \\ &=E(X^3)-3\mu E(X^2)+2\mu^3 \quad (E(X)=\muより) \end{align} $$
したがって、
$$ \alpha_3=\frac{E(X^3)-3\mu E(X^2)+2\mu^3 }{\sigma^3} $$
となります。
(1) 例3のコイン投げの確率変数 \( X \) に対して、確率分布の歪度 \( \alpha_3 \) を求める。
例3より、
$$ E(X)=\frac{3}{2}, \quad E(X^2)=3, $$
$$ V(X)=E(X^2)-\{E(X)\}^2=3-\frac{9}{4}=\frac{3}{4}, \quad \sigma=\sqrt{\frac{3}{4}} $$
また、
$$ E(X^3)=0^3\times \frac{1}{8}+1^3\times \frac{3}{8}+2^3\times\frac{3}{8}+3^3\times \frac{1}{8}=\frac{27}{4} $$
したがって、
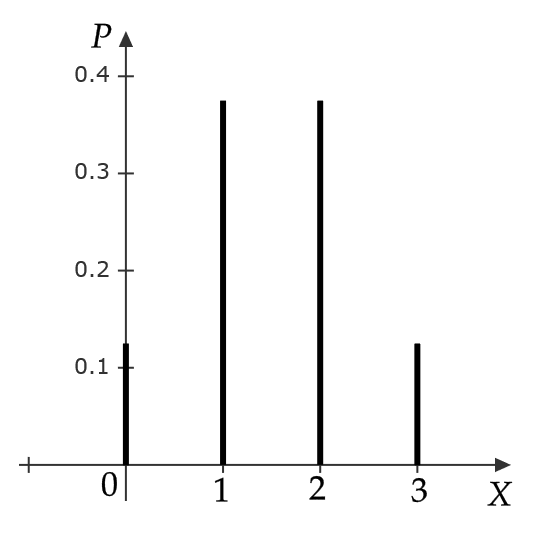
$$ \alpha_3=\frac{E(X^3)-3\mu E(X^2)+2\mu^3 }{\sigma^3}=\frac{\frac{27}{4}-3\times\frac{3}{2}\times 3+2\left( \frac{3}{2} \right)^3}{\frac{3}{4}\sqrt{\frac{3}{4}}}=0 $$
よって、確率分布は左右対称であることがわかる。
実際、確率分布のグラフは次のようになる。
(2) 例3のコイン投げにおけるコインが歪んでいて、表と裏の出る確率が異なっていた。
表が出る確率が \( \frac{1}{4} \) 、裏が出る確率が \( \frac{3}{4} \) とするとき、確率分布の歪度 \( \alpha_3 \) を求める。
まず、確率分布を求めると、
| \( X \) | \( 0 \) | \( 1 \) | \( 2 \) | \( 3 \) | 計 |
| \( P \) | \( \frac{27}{64} \) | \( \frac{27}{64} \) | \( \frac{9}{64} \) | \( \frac{1}{64} \) | \( 1 \) |
このとき、
$$ E(X)=0\times \frac{27}{64}+1\times \frac{27}{64}+2\times\frac{9}{64}+3\times \frac{1}{64}=\frac{3}{4} $$
$$ E(X^2)=0^2\times \frac{27}{64}+1^2\times \frac{27}{64}+2^2\times\frac{9}{64}+3^2\times \frac{1}{64}=\frac{9}{8} $$
$$ V(X)=E(X^2)-\{E(X)\}^2=\frac{9}{8}-\frac{9}{16}=\frac{9}{16}, \quad \sigma=\frac{3}{4} $$
$$ E(X^3)=0^3\times \frac{27}{64}+1^3\times \frac{27}{64}+2^3\times\frac{9}{64}+3^3\times \frac{1}{64}=\frac{63}{32} $$
したがって、
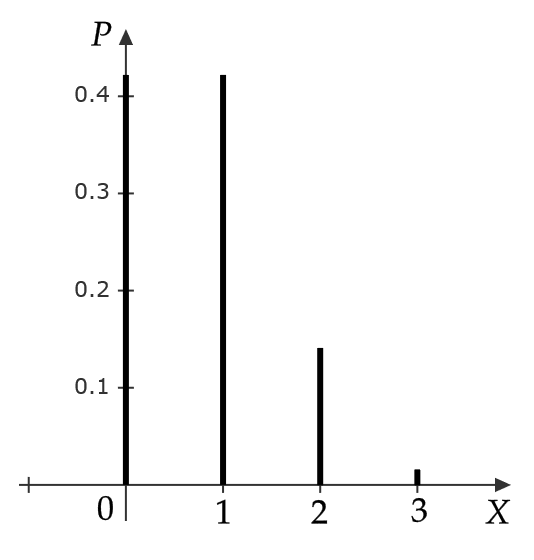
$$ \alpha_3=\frac{E(X^3)-3\mu E(X^2)+2\mu^3 }{\sigma^3}=\frac{\frac{63}{32}-3\times\frac{3}{4}\times \frac{9}{8}+2\left( \frac{3}{4} \right)^3}{\left( \frac{3}{4} \right)^3}=\frac{2}{3}>0 $$
よって、確率分布は右に裾が長い分布であることがわかる。
実際、確率分布のグラフは次のようになる。
尖度
確率変数 \( X \) の確率分布の尖度(せんど)を次で定めます。
確率変数 \( X \) に対して、平均を \( \mu \) 、標準偏差を \( \sigma \) とおく。
このとき、 \( X \) の確率分布の尖度 \( \alpha_4 \) を次で定める。
$$ \alpha_4=\frac{E[(X-\mu)^4]}{\sigma^4} $$
ただし、 \( \alpha_4-3 \) を確率分布の尖度ということもある。
これは、確率分布の中心のとがり具合を表す指標となっています。
今後解説する正規分布といわれる確率分布は次のような形をしています。
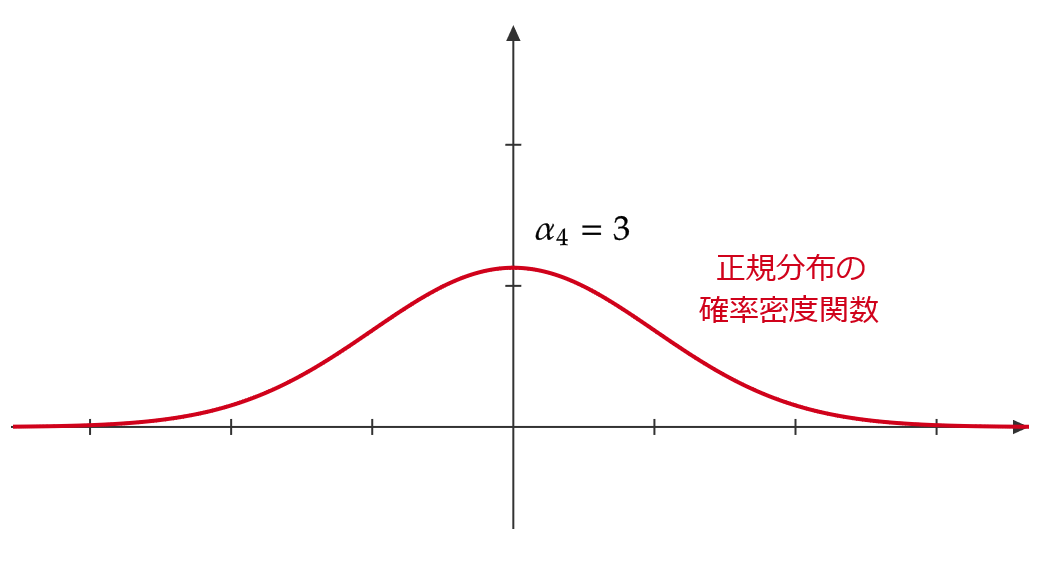
この正規分布の尖度が \( \alpha_4=3 \) であるので、 \( \alpha_4-3>0 \) のときは正規分布よりとがった確率分布、 \( \alpha_4-3<0 \) のときは正規分布より丸い確率分布となります。
また、尖度は定義通りに計算するのは大変なので、分子を変形をすると、
$$ \begin{align} E[(X-\mu)^4]&=E[X^4-4\mu X^3+6\mu^2X^2-4\mu^3 X+\mu^4] \\ &=E(X^4)-4\mu E(X^3)+6\mu^2E(X^2)-4\mu^3E(X)+\mu^4 \\ &=E(X^4)-4\mu E(X^3)+6\mu^2E(X^2)-3\mu^4 \quad (E(X)=\muより) \end{align} $$
したがって、
$$ \alpha_4=\frac{E(X^4)-4\mu E(X^3)+6\mu^2E(X^2)-3\mu^4}{\sigma^4} $$
となります。
例5の確率変数 \( X \) とその確率密度関数で \( a=0,b=1 \) としたもの
$$ f(x)=\begin{cases} 1 & (x\in [0,1]) \\ 0 & (それ以外) \end{cases} $$
を考える。このとき、尖度 \( \alpha_4 \) を求める。
例5より、
$$ E(X)=\frac{1}{2}, \quad E(X^2)=\frac{1}{3}, \quad V(X)=\frac{1}{12}, \quad \sigma=\frac{1}{2\sqrt{3}} $$
また、
$$ \begin{align} E(X^3)&=\int_{-\infty}^{\infty}x^3f(x)dx=\int_0^1x^3dx \quad (x\not\in[0,1]ではf(x)=0) \\ &=\left[ \frac{1}{4}x^4 \right]_0^1=\frac{1}{4} \end{align} $$
$$ \begin{align} E(X^4)&=\int_{-\infty}^{\infty}x^4f(x)dx=\int_0^1x^4dx \quad (x\not\in[0,1]ではf(x)=0) \\ &=\left[ \frac{1}{5}x^5 \right]_0^1=\frac{1}{5} \end{align} $$
したがって、
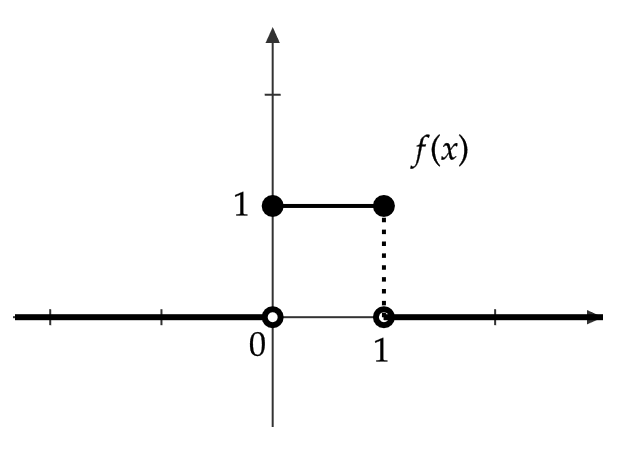
$$ \begin{align} \alpha_4&=\frac{E(X^4)-4\mu E(X^3)+6\mu^2E(X^2)-3\mu^4}{\sigma^4} \\ &=\frac{\frac{1}{5}-4\times \frac{1}{2}\times \frac{1}{4}+6\times \left( \frac{1}{2} \right)^2\times \frac{1}{3}-3\times \left( \frac{1}{2} \right)^4}{\left( \frac{1}{2\sqrt{3}} \right)^4} \\ &=\frac{9}{5} \end{align} $$
よって、 \( \frac{9}{5}-3=-\frac{6}{5}<0 \) より、正規分布より丸い確率分布となる。
実際、確率分布のグラフは次のようになる。
モーメントとモーメント母関数
モーメント(積率)
これまで、確率変数 \( X \) に対して、
$$ E(X), \quad E(X^2), \quad E(X^3), \quad E(X^4) $$
を計算してきました。もちろん、もっと一般に \( X^n \) の期待値を考えることもできます。
確率変数 \( X \) に対して、 \( E(X^n)=\mu’_n \) を原点の周りの \( n \) 次モーメント( \( n \) 次の積率) という。
また、 \( E(X)=\mu \) とするとき、 \( E[(X-\mu)^n]=\mu_n \) を期待値の周りの \( n \) 次モーメントという。
このとき、 \( \mu’_1 \) は \( X \) の期待値、 \( \mu_2 \) は \( X \) の分散、 \( \frac{\mu_3}{\sigma^3} \) は \( X \) の確率分布の歪度、 \( \frac{\mu_4}{\sigma^4} \) は \( X \) の確率分布の尖度となります。
モーメント母関数(積率母関数)
では、この \( n \) 次モーメントを簡単に求める方法はあるのでしょうか。
そのために、次のモーメント母関数(積率母関数)を考えます。
確率変数 \( X \) に対して、モーメント母関数(積率母関数) \( M_X(t) \) を次で定める。
$$ M_X(t)=E(e^{tX})=\begin{cases} \displaystyle \sum_{i=1}^{\infty}e^{tx_i}p_i & (Xが離散型確率変数) \\ \displaystyle \int_{-\infty}^{\infty}e^{tx}f(x)dx & (Xが連続型確率変数) \end{cases} $$
これを用いて \( n \) 次モーメントを求めてみましょう。
\( e^{tX} \) を \( t \) で微分すると、 \( Xe^{tX} \) であるので、
$$ M’_X(t)=E(Xe^{tX}) $$
これを繰り返すと、
$$ M^{(n)}_X(t)=E(X^ne^{tX}) $$
したがって、 \( t=0 \) を代入すると、
$$ M^{(n)}_X(0)=E(X^ne^{0})=E(X^n)=\mu’_n \quad (n=1,2,\cdots) $$
これにより、 \( E(X) \) と \( V(X) \) は
$$ E(X)=M’_X(0), \quad V(X)=E(X^2)-\{ E(X) \}^2=M^{\prime\prime}_X(0)-\{ M’_X(0) \}^2 $$
で求められます。
(1) 例7(2)の状況における確率変数 \( X \) に対して、モーメント母関数を用いて期待値と分散を求める。
$$ \begin{align} M_X(t)&=E(e^{tX})=e^{0t}\times \frac{27}{64}+e^{t}\times \frac{27}{64}+e^{2t}\times\frac{9}{64}+e^{3t}\times \frac{1}{64} \\ &=\frac{1}{64}(e^{3t}+9e^{2t}+27e^t+27) \end{align} $$
よって、
$$ M’_X(t)=\frac{1}{64}(3e^{3t}+18e^{2t}+27e^t) $$
$$ M^{\prime\prime}_X(t)=\frac{1}{64}(9e^{3t}+36e^{2t}+27e^t) $$
したがって、
$$ E(X)=M’_X(0)=\frac{1}{64}(3e^{0}+18e^{0}+27e^0)=\frac{48}{64}=\frac{3}{4} $$
$$ \begin{align} V(X)&=M^{\prime\prime}_X(0)-\{ M’_X(0) \}^2 \\ &=\frac{1}{64}(9e^{0}+36e^{0}+27e^0)-\left( \frac{3}{4} \right)^2 \\ &=\frac{72}{64}-\frac{9}{16}=\frac{9}{16} \end{align} $$
よって、例7(2)と同じ結果となる。
(2) 例2(2)と例5(2)の確率変数 \( X \) とその確率密度関数
$$ f(x)=\begin{cases} \frac{1}{b-a} & (x\in [a,b]) \\ 0 & (それ以外) \end{cases} $$
を考える。このとき、モーメント母関数を用いて期待値と分散を求める。
$$ \begin{align} M_X(t)&=E(e^{tX})=\int_{-\infty}^{\infty}e^{tx}f(x)dx=\int_a^be^{tx}\frac{1}{b-a}dx \quad (x\not\in[a,b]ではf(x)=0) \\ &=\frac{1}{b-a}\left[ \frac{1}{t}e^{tx} \right]_a^b=\frac{e^{bt}-e^{at}}{t(b-a)} \end{align} $$
よって、商の微分公式より、
$$ M’_X(t)=\left(\frac{e^{bt}-e^{at}}{t(b-a)}\right)’=\frac{(be^{bt}-ae^{at})t-(e^{bt}-e^{at})}{t^2(b-a)} $$
$$ M^{\prime\prime}_X(t)=\frac{\{(b^2e^{bt}-a^2e^{at})t^2 \}-2\{ (be^{bt}-ae^{at})t-(e^{bt}-e^{at})\}}{t^3(b-a)} $$
ここで、 \( M’_X(0), \ M^{\prime\prime}_X(0) \) を求めたいが、分母分子がともに \( 0 \) になってしまうのでロピタルの定理を用いる必要がある。
$$ \begin{align} M’_X(0)&=\frac{(be^{bt}-ae^{at})t-(e^{bt}-e^{at})}{t^2(b-a)}|_{t=0} \\ &=\lim_{t\to0} \frac{(be^{bt}-ae^{at})t-(e^{bt}-e^{at})}{t^2(b-a)} \quad (tに関して連続であるため) \\ &=\lim_{t\to0}\frac{b^2e^{bt}-a^2e^{at}}{2(b-a)} \quad (ロピタルの定理) \\ &=\frac{b^2e^0-a^2e^0}{2(b-a)}=\frac{a+b}{2} \end{align} $$
$$ \begin{align} M^{\prime\prime}_X(0)&=\lim_{t\to0}\frac{\{(b^2e^{bt}-a^2e^{at})t^2 \}-2\{ (be^{bt}-ae^{at})t-(e^{bt}-e^{at})\}}{t^3(b-a)} \\ &=\lim_{t\to0}\frac{b^3e^{bt}-a^3e^{at}}{3(b-a)} \quad (ロピタルの定理) \\ &=\frac{b^3e^0-a^3e^0}{3(b-a)}=\frac{b^2+ab+a^2}{3} \end{align} $$
(途中式を大きく省略しているので、きちんと計算するとかなり大変)
したがって、
$$ E(X)=M’_X(0)=\frac{a+b}{2} $$
$$ \begin{align} V(X)&=M^{\prime\prime}_X(0)-\{ M’_X(0) \}^2 \\ &=\frac{b^2+ab+a^2}{3}-\frac{(a+b)^2}{4}=\frac{(b-a)^2}{12} \end{align} $$
よって、例2(2)と例5(2)の結果と同じになる。
(同じにはなるが、この場合モーメント母関数を用いると逆に計算が大変になってしまう)
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

