確率・統計(統計検定2級対応)07：確率変数と確率分布

2023年8月11日2024年3月25日

こんにちは、ひかりです。

今回は確率・統計から確率変数と確率分布について解説していきます。

この記事では以下のことを紹介します。

確率変数と分布関数について
離散確率分布について
連続確率分布について

確率変数と分布関数

まず、次の例を考えます。

例1

1個のさいころを投げて、1の目が出るときは300円、2または3の目が出るときは200円、4以上の目が出るときは100円がもらえるとする。

このとき、300円がもらえる確率は $ \frac{1}{6} $ 、200円がもらえる確率は $ \frac{2}{6}=\frac{1}{3} $ 、300円がもらえる確率は $ \frac{3}{6}=\frac{1}{2} $ である。

ここで、さいころを投げてもらえるお金の金額を $ X $ 円とする。

すると、 $ X $ は100か200か300のどれかの値をとる変数であり、 $ X $ がどの値をとるかはさいころ投げの結果によって変わる。

また、 $ X=100 $ となる確率を $ P(X=100) $ と表すとすると、これは4以上の目が出る確率であるので、

$$ P(X=100)=\frac{3}{6}=\frac{1}{2} $$

同様に、 $ X≦200 $ となる確率 $ P(X≦200) $ は

$$ P(X≦200)=P(X=100もしくは200)=\frac{2+3}{6}=\frac{5}{6} $$

この例の $ X $ のように、各値に対して確率が定まっているような変数のことを確率変数といいます。

確率変数は $ X,Y,Z $ などと表すことが多いです。

この例では $ P(X≦200) $ の確率を求めましたが、これを一般化したものを考えます。

定義1 (分布関数)

$ X $ を確率変数、 $ x $ を任意の実数とする。

このとき、確率 $ P(X≦x) $ を考えると、これは $ x $ の関数となる。

この $ P(X≦x) $ を確率変数 $ X $ の分布関数または累積分布関数といい、 $ F(x) $ で表す。

例2

例1のさいころ投げを考える。

このとき、 $ x<100 $ のとき

$$ P(X≦x)=P(\emptyset)=0 $$

$ 100≦x<200 $ のとき

$$ P(X≦x)=P(X=100)=\frac{1}{2} $$

$ 200≦x<300 $ のとき

$$ P(X≦x)=P(X=100または200)=\frac{2+3}{6}=\frac{5}{6} $$

$ 300≦x $ のとき

$$ P(X≦x)=P(X=100または200または300)=P(\Omega)=1 $$

したがって、分布関数 $ F(x) $ は次で与えられる。

$$ F(x)=\begin{cases} 0 & (x<100) \\ \frac{1}{2} & (100≦x<200) \\ \frac{5}{6} & (200≦x<300) \\ 1 & (300≦x) \end{cases} $$

$ F(x) $ のグラフは次のようになる。

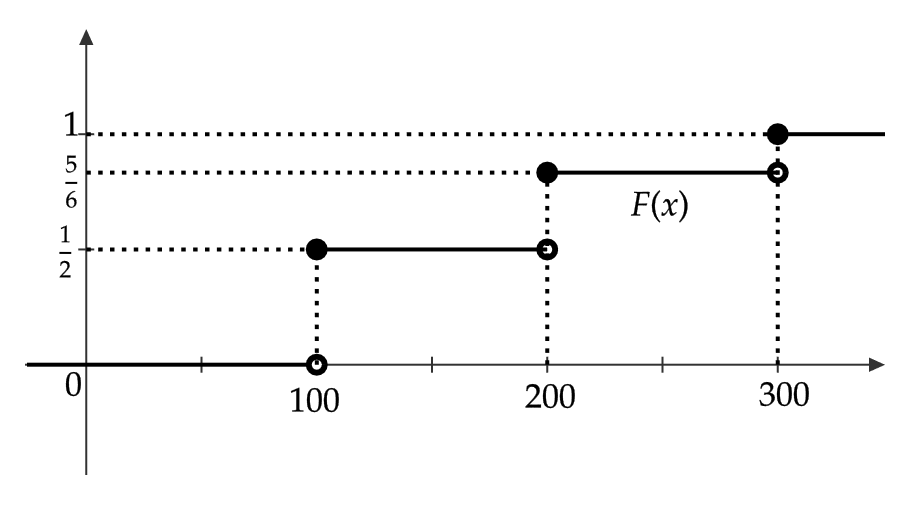
分布関数 $ F(x) $ のグラフをながめると、次のような分布関数の性質が成り立つことが分かります。

定理1 (分布関数の性質)

分布関数 $ F(x) $ は次の性質をみたす。

(1)　$ 0≦F(x)≦1 $

(2)　$ F(x) $ は非減少関数である。すなわち、

$$ x<y \Rightarrow F(x)≦F(y) $$

(3)　$$ \lim_{x\to -\infty}F(x)=0, \quad \lim_{x\to \infty}F(x)=1 $$

(4)　$ F(x) $ は右連続である。すなわち、

$$ \lim_{x\to a+0}F(x)=F(a) $$

(5)　$$ P(a<X≦b)=F(b)-F(a) $$

厳密な証明はここでは省略します。

離散確率分布について

再び、例1のさいころ投げを考えます。

例3

例1のさいころ投げにてもらえるお金の金額を表す確率変数 $ X $ に対して、 $ X $ のとる値とそれに対応する確率を表に表すと次のようになる。

$ X $	$ 100 $	$ 200 $	$ 300 $	計
$ P $	$ \frac{1}{2} $	$ \frac{1}{3} $	$ \frac{1}{6} $	$ 1 $

この表のように、確率変数のとる値とその値をとる確率との対応を示したものを、その確率変数の確率分布または分布といい、確率変数 $ X $ はこの分布に従うといいます。

また、これは次で定義する離散確率分布となっています。

定義2 (離散確率分布)

確率変数 $ X $ のとりうる値が $ x_1,x_2,\cdots $ (有限個でもよい)で各事象 $ \{X=x_i \} $ に対して、確率 $ p(x_i)=P(X=x_i) $ が対応しているとき、 $ X $ を離散型確率変数といい、 $ X $ が従う確率分布を離散確率分布という。

また、関数 $ p(x_i) $ を確率変数 $ X $ の確率関数という。

一般に、離散型確率変数 $ X $ のとる値が $ x_1,x_2,\cdots,x_n $ であるとき、

$$ p(x_i)=P(X=x_i)=p_i $$

とすると、確率の定義から次が成り立ちます。

$$ p_1≧0, \quad p_2≧0, \quad \cdots, \quad p_n≧0 $$

$$ p_1+p_2+\cdots+p_n=\sum_{i=1}^np_i=1 $$

このとき、 $ X $ の確率分布は次のような表で表されます。

$ X $	$ x_1 $	$ x_2 $	$ \cdots $	$ x_n $	計
$ P $	$ p_1 $	$ p_2 $	$ \cdots $	$ p_n $	$ 1 $

また、 $ X $ の分布関数 $ F(x) $ は次のように表されます。

$$ F(x)=\sum_{x_i≦x} P(X=x_i) $$

(つまり、 $ x $ 以下の $ x_i $ の確率 $ p_i $ をすべて足したものとなります。)

例4

白球4個と黒球3個が入っている袋から同時に2個の球を取り出すとき、その中に含まれている白球の個数 $ X $ の確率分布を求める。

$ X $ は $ 0,1,2 $ をとる確率変数であり、それぞれの値をとる確率は

$$ P(X=0)=\frac{{}_3C_2}{{}_7C_2}=\frac{\frac{3\cdot2}{2\cdot 1}}{\frac{7\cdot 6}{2\cdot 1}}=\frac{1}{7} $$

$$ P(X=1)=\frac{{}_4C_1\times{}_3C_1}{{}_7C_2}=\frac{4\times 3}{\frac{7\cdot 6}{2\cdot 1}}=\frac{4}{7} $$

$$ P(X=2)=\frac{{}_4C_2}{{}_7C_2}=\frac{\frac{4\cdot3}{2\cdot 1}}{\frac{7\cdot 6}{2\cdot 1}}=\frac{2}{7} $$

したがって、 $ X $ の確率分布は次のようになる。

$ X $	$ 0 $	$ 1 $	$ 2 $	計
$ P $	$ \frac{1}{7} $	$ \frac{4}{7} $	$ \frac{2}{7} $	$ 1 $

また、分布関数 $ F(x) $ を求めると、

$$ F(x)=\begin{cases} 0 & (x<0) \\ \frac{1}{7} & (0≦x<1) \\ \frac{5}{7} & (1≦x<2) \\ 1 & (2≦x) \end{cases} $$

となり、グラフは次のようになる。

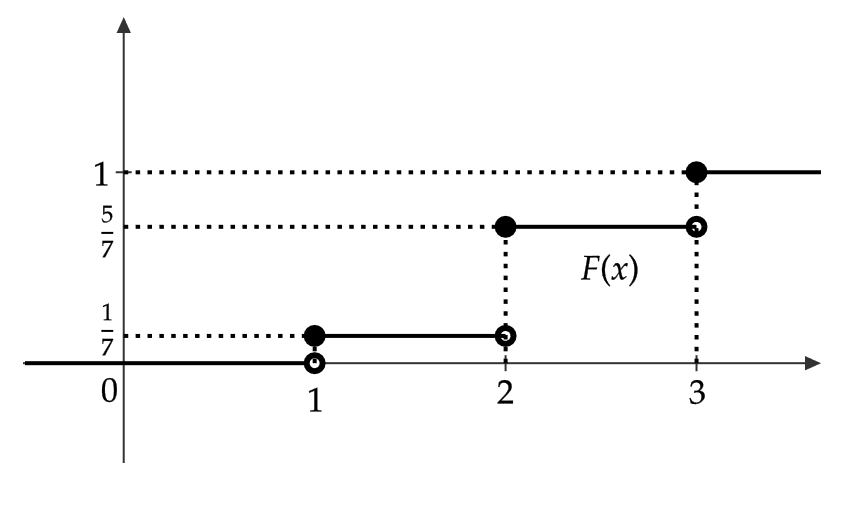
離散型確率変数 $ X $ のとる値が有限でなく、 $ x_1,x_2,\cdots $ であるときも同様のことが成り立ちます。

つまり、 $ p(x_i)=P(X=x_i)=p_i $ とすると、

$$ p_i≧0, \quad (i=1,2,\cdots) $$

$$ p_1+p_2+\cdots=\sum_{i=1}^{\infty}p_i=1 $$

$$ F(x)=\sum_{x_i≦x} P(X=x_i) $$

例5

ある交差点における1日の交通事故の件数を $ X $ とおくと、次のような確率関数 $ p(k) $ となることがわかった。

$$ p(k)=P(X=k)=\frac{1}{k!}e^{-1} \quad (k=0,1,2,\cdots) $$

(つまり、 $ k $ が1日の交通事故の件数である。)

いくつかの値での確率を求めてみると、

$$ p(0)=P(X=0)=e^{-1}=0.368 $$

$$ p(1)=P(X=1)=e^{-1}=0.368 $$

$$ p(2)=P(X=2)=\frac{1}{2}e^{-1}=0.184 $$

これをグラフにすると、次のようになる。

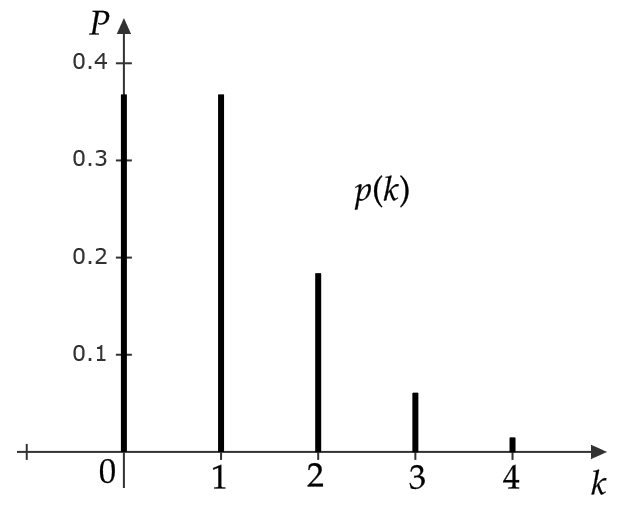
これが確率変数 $ X $ が従う確率分布である。

(これは後に学ぶことになるポアソン分布というものになっています。)

また、分布関数 $ F(x) $ は次のようになる。

$$ F(x)=\begin{cases} 0 & (x<0) \\ \sum_{k≦x}\frac{1}{k!}e^{-1} & (x≧0) \end{cases} $$

連続確率分布について

確率分布にはもう一つ種類があります。

定義3 (連続確率分布)

任意の区間 $ I $ に対して、 $ X $ のとる値が $ I $ に入っている確率を $ P(X \in I) $ と表すとき、

$$ P(X\in I)=\int_If(x)dx $$

となる関数 $ f(x) $ が存在するならば、 $ X $ を連続型確率変数といい、 $ f(x) $ を $ X $ の確率密度関数という。

また、 $ X $ が従う分布を連続確率分布という。

一般に、連続型確率変数 $ X $ の確率密度関数が $ f(x) $ であるとき、確率の定義から次が成り立ちます。

$$ f(x)≧0, \quad \int_{-\infty}^{\infty}f(x)dx=1 $$

また、 $ X $ の分布関数 $ F(x) $ は次のように表されます。区間 $ I $ を $ (-\infty,x] $ としてみてあげると、

$$ F(x)=P(X≦x)=\int_{-\infty}^xf(t)dt $$

この関係式より、 $ F(x) $ が微分可能な点に関しては

$$ \frac{dF(x)}{dx}=f(x) $$

となります。また、 $ I=(a,b] $ とすれば、

$$ P(a<X≦b)=\int_a^bf(x)dx $$

さらに、 $ I=\{ a \} $ とすれば、

$$ P(X=a)=\int_a^af(x)dx=0 $$

となり、離散型確率変数で考えてきた1点での $ X $ の確率というのは、連続型確率変数では必ず0になります。

例6

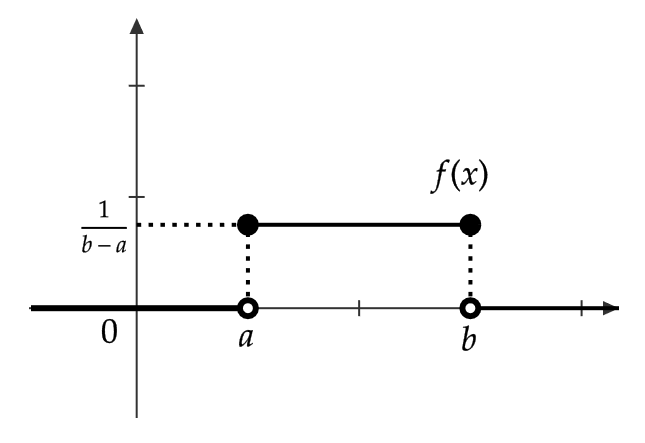
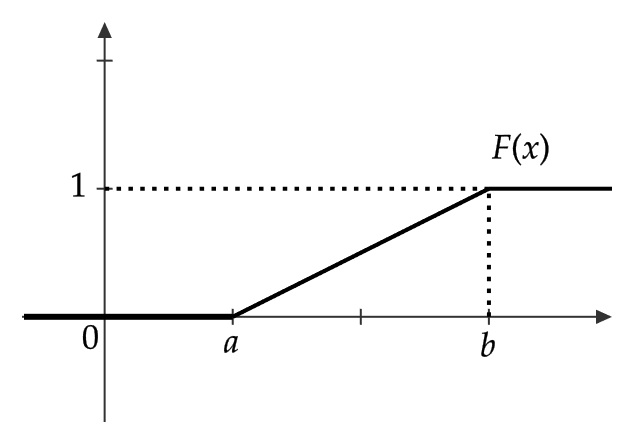
連続型確率変数 $ X $ の確率密度関数 $ f(x) $ が

$$ f(x)=\begin{cases} \frac{1}{b-a} & (x\in [a,b]) \\ 0 & (それ以外) \end{cases} $$

のとき、いくつか確率を求めてみると、

$$ \begin{align} P(X≦b)&=\int_{-\infty}^bf(x)dx=\int_a^bf(x)dx \quad (x<a \ で \ f(x)=0) \\ &=\int_a^b\frac{1}{b-a}dx=\frac{1}{b-a}[x]^b_a=\frac{1}{b-a}(b-a)=1 \end{align} $$

$$ \begin{align} P\left(\frac{a+b}{2}<X\right)&=\int_{\frac{a+b}{2}}^{\infty}f(x)dx=\int_{\frac{a+b}{2}}^bf(x)dx \quad (b<x \ で \ f(x)=0) \\ &=\int_{\frac{a+b}{2}}^b\frac{1}{b-a}dx=\frac{1}{b-a}[x]^b_{\frac{a+b}{2}}=\frac{1}{b-a}(b-\frac{a+b}{2})=\frac{1}{2} \end{align} $$

また、分布関数 $ F(x) $ を求める。まず、 $ x<a $ のときは $ f(x)=0 $ であるので、

$$ F(x)=P(X≦x)=\int_{-\infty}^xf(t)dt=0 $$

$ a≦x<b $ のときは

$$ \begin{align} F(x)&=P(X≦x)=\int_{-\infty}^xf(t)dt=\int_a^xf(t)dt \\ &=\int_a^x\frac{1}{b-a}dt=\frac{1}{b-a}[t]^x_a=\frac{x-a}{b-a} \end{align} $$

$ b≦x $ のときは

$$ \begin{align} F(x)&=P(X≦x)=\int_{-\infty}^xf(t)dt=\int_a^bf(t)dt \\ &=\int_a^b\frac{1}{b-a}dt=\frac{1}{b-a}[t]^b_a=1 \end{align} $$

したがって、

$$ F(x)=\begin{cases} 0 & (x<a) \\ \frac{x-a}{b-a} & (a≦x<b) \\ 1 & (b≦x) \end{cases} $$

である。最後に、 $ f(x) $ と $ F(x) $ のグラフは次のようになります。