こんにちは、ひかりです。
今回は確率・統計から条件付き確率と確率の独立性について解説していきます。
この記事では以下のことを紹介します。
- 条件付き確率について
- 確率の独立性と反復試行について
- ベイズの定理について
条件付き確率
ある事象が起きている状況のもと、ほかの事象の確率を求めることを考えます。
このとき、用いられるのが条件付き確率であり、次のように定義されます。
\( P(A)>0 \) をみたす事象 \( A \) が起こったときに事象 \( B \) の起こる確率を、 \( P(B|A) \) と表し \( A \) が起こるという条件の下での \( B \) の条件付き確率という。 \( P(B|A) \) は次であたえられる。
$$ P(B|A)=\frac{P(A\cap B)}{P(A)} $$
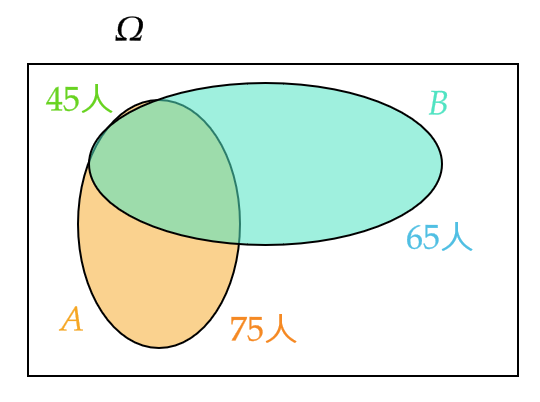
100人の子供にアンケートしたところ、サッカーが好きな子供は75人、野球が好きな子供は65人、どちらも好きな子供は45人いることがわかった。
このとき、サッカーが好きな子供の中から1人を選ぶとき、その子供が野球も好きである確率を求める。
選んだ子供がサッカーが好きである事象を \( A \) 、野球が好きである事象 \( B \) とすると、求めたい確率は \( P(B|A) \) である。
$$ P(A)=\frac{75}{100}, \quad P(A\cap B)=\frac{45}{100} $$
より、
$$ P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{\frac{45}{100}}{\frac{75}{100}}=\frac{3}{5} $$
図で表すと、次のようになる。
条件付き確率から、次の公式が得られます。
(1) (確率の乗法公式)
\( P(A)>0 \) となる事象 \( A \) と任意の事象 \( B \) に対して、次が成り立つ。
$$ P(A\cap B)=P(A)P(B|A) $$
(2) (全確率の公式)
全事象 \( \Omega \) を互いに排反な \( n \) 個の事象 \( A_1,A_2,\cdots,A_n \) に分割する。つまり、
$$ A_i\cap A_j=\emptyset \ (i\not=j), \quad A_1\cup A_2\cup \cdots \cup A_n=\Omega $$
このとき、任意の事象 \( B \) に対して、次が成り立つ。
$$ P(B)=\sum_{i=1}^nP(A_i)P(B|A_i) $$
定理1の証明(気になる方だけクリックしてください)
(1) 条件付き確率の定義
$$ P(B|A)=\frac{P(A\cap B)}{P(A)} $$
の両辺に \( P(A) \) をかければ得られます。
(2) \( A_i\cap A_j=\emptyset \ (i\not=j) \) より、
$$ (A_i\cap B)\cap (A_j\cap B)=(A_i\cap A_j)\cap B=\emptyset \cap B=\emptyset $$
であり、
$$ \begin{align} B&=\Omega\cap B=(A_1\cup A_2\cup \cdots A_n)\cap B \\ &=(A_1\cap B)\cup (A_2\cap B)\cup \cdots (A_n\cap B) \end{align} $$
したがって、
$$ A_1\cap B, \quad A_2\cap B, \quad \cdots, \quad A_n\cap B $$
は互いに排反なので、確率の加法定理と(1)より、
$$ P(B)=\sum_{i=1}^nP(A_i\cap B)=\sum_{i=1}^nP(A_i)P(B|A_i) $$
(1) 白球4個、黒球2個が入っている袋から、1個ずつ続けて2個の球を取り出すとき、2個とも白球である確率を求める。
最初に白球を取り出す事象を \( A \) 、2回目に白球を取り出す事象を \( B \) とすると、求める確率は \( P(A\cap B) \) である。ここで、
$$ P(A)=\frac{4}{6}, \quad P(B|A)=\frac{4-1}{6-1}=\frac{3}{5} $$
( \( P(B|A) \) はつまり白球3個、黒球2個の入っている袋から、1個白球を取り出す確率となる)
したがって、確率の乗法公式より、
$$ P(A\cap B)=P(A)P(B|A)=\frac{4}{6}\cdot \frac{3}{5}=\frac{2}{5} $$
(2) 当たりが \( m \) 本、はずれが \( n \) 本あるくじを2人の人が引くとき、初めにくじを引くのと後からくじを引くのとではどちらが有利かを求める。
初めにくじを引く人が当たる事象を \( A \) 、後からくじを引く人が当たる事象を \( B \) とする。
全事象 \( \Omega \) を \( A \) と \( A^c \) に分割すると、全確率の公式より、
$$ P(B)=P(A)P(B|A)+P(A^c)P(B|A^c) $$
ここで、
$$ P(A)=\frac{n(A)}{n(\Omega)}=\frac{m}{m+n}, \quad P(A^c)=\frac{n(A^c)}{n(\Omega)}=\frac{n}{m+n} $$
であり、また、
$$ P(B|A)=\frac{m-1}{m+n-1}, \quad P(B|A^c)=\frac{m}{m+n-1} $$
( \( P(B|A) \) はつまり当たりが \( m-1 \) 本、はずれが \( n \) 本あるくじから、当たりのくじを引く確率となる)
したがって、
$$ \begin{align} P(B)&=P(A)P(B|A)+P(A^c)P(B|A^c) \\ &=\frac{m}{m+n}\frac{m-1}{m+n-1}+\frac{n}{m+n}\frac{m}{m+n-1}=\frac{m}{m+n} \end{align} $$
であるので、 \( P(A)=P(B) \) となり、くじを引く順序に有利・不利はない。
確率の独立性と反復試行
確率の独立性
確率の独立性を次のように定義します。
2つの事象 \( A,B \) について、一方の事象が起こるかどうかが他方の事象の起こる確率に影響しないとき、 \( A \) と \( B \) は独立という。
つまり、次の式が成り立つとき、 \( A \) と \( B \) は独立という。
$$ P(A\cap B)=P(A)P(B) $$
なぜこの式で \( A \) と \( B \) が独立であるというのかを見ていきましょう。
$$ P(A\cap B)=P(A)P(B) $$
が成り立つと、 \( P(A)>0 \) において条件付き確率は次のように表されます。
$$ P(B|A)=\frac{P(A\cap B)}{P(A)}=\frac{P(A)P(B)}{P(A)}=P(B) $$
これは、つまり \( A \) という条件のもとでの \( B \) の確率が \( A \) という条件をつけない \( B \) の確率と等しいということを言っています。
したがって、 \( A \) という条件は \( B \) の確率に何も影響を与えないということになります。
同様に \( P(B)>0 \) において \( P(A|B)=P(A) \) も成り立つので、 \( B \) という条件は \( A \) の確率に何も影響を与えないということになります。
このことから、
$$ P(A\cap B)=P(A)P(B) $$
が独立性の定義となっています。
1個のさいころを投げるとき、偶数の目が出る事象を \( A \) 、3の倍数の目が出る事象を \( B \) 、4以上の目が出る事象を \( C \) とするとき、 \( A \) と \( B \) 、 \( A \) と \( C \) が独立かどうかを調べる。
事象 \( A,B,C \) の確率は
$$ P(A)=\frac{3}{6}=\frac{1}{2}, \quad P(B)=\frac{2}{6}=\frac{1}{3}, \quad P(C)=\frac{3}{6}=\frac{1}{2} $$
であり、また、
$$ P(A\cap B)=\frac{1}{6}, \quad P(A\cap C)=\frac{2}{6}=\frac{1}{3} $$
したがって、
$$ P(A\cap B)=P(A)P(B), \quad P(A\cap C)\not=P(A)P(C) $$
であるので、事象 \( A \) と \( B \) は独立であり、事象 \( A \) と \( C \) は独立ではない。
3つ以上の事象の独立性には少し注意が必要です。
3つの事象 \( A,B,C \) が次をみたすとき、事象 \( A,B,C \) はたがいに独立であるという。
$$ P(A\cap B)=P(A)P(B), \quad P(A\cap C)=P(A)P(C), $$
$$ P(B\cap C)=P(B)P(C), \quad P(A\cap B\cap C)=P(A)P(B)P(C) $$
さいころを投げて出た目を見る試行において、次の3つの事象を考える。
$$ A=\{ 1,3,5,6 \}, \quad B=\{ 2,4,6 \}, \quad C=\{ 2,4,6 \} $$
このとき、
$$ P(A\cap B\cap C)=P(\{ 6 \} )=\frac{1}{6} $$
$$ P(A)P(B)P(C)=\frac{4}{6}\cdot \frac{3}{6}\cdot \frac{3}{6}=\frac{1}{6} $$
より、
$$ P(A\cap B\cap C)=P(A)P(B)P(C) $$
しかし、事象 \( B \) と \( C \) の独立性を見ると、
$$ P(B\cap C)=P(\{2,4,6 \})=\frac{3}{6}=\frac{1}{2} $$
$$ P(B)P(C)=\frac{3}{6}\cdot \frac{3}{6}=\frac{1}{4} $$
より、
$$ P(B\cap C)\not=P(B)P(C) $$
となるので、事象 \( B \) と \( C \) は独立ではない。
したがって、 \( P(A\cap B\cap C)=P(A)P(B)P(C) \) だけでは、3つの事象は互いに独立であるとは定義できない。
3つの事象の独立性を参考にしつつ、一般の事象の独立性の定義をご覧ください。
\( n \) 個の事象 \( A_1,A_2,\cdots,A_n \) が互いに独立であるとは、任意の \( k \) 個 \( (2≦k≦n) \) の事象の組 \( A_{\lambda_1},A_{\lambda_2},\cdots,A_{\lambda_k} \) に対して、
$$ P(A_{\lambda_1}A_{\lambda_2}\cdots A_{\lambda_k})=P(A_{\lambda_1})P(A_{\lambda_2})\cdots P(A_{\lambda_k}) $$
が成り立つことをいう。
反復試行
さいころをくり返し投げるように、同じ条件のもとで同じ試行を繰り返し行うとすることを考えます。
それらの試行が独立であるとき、これらの試行をまとめて反復試行といいます。
反復試行の確率は次で与えられます。
事象 \( A \) が起こる確率を \( p \) 、その余事象の確率を \( q=1-p \) とする試行を考える。
その試行を \( n \) 回くり返す反復試行において、事象 \( A \) が \( r \) 回起こる確率は次で与えられる。
$$ {}_nC_rp^rq^{n-r} \quad (r=0,1,2,\cdots,n) $$
赤球3個と白球6個の入った袋から1個の袋を取り出し、色を調べてから元に戻す。
これを5回くり返すとき、赤球をちょうど2回取り出す確率を求める。
反復試行の確率の公式より、
$$ {}_5C_2\left( \frac{3}{9} \right)^2\left( \frac{6}{9} \right)^{5-2}=\frac{5\cdot 4}{2\cdot 1}\times \left( \frac{1}{3} \right)^2 \left( \frac{2}{3} \right)^3=\frac{80}{243} $$
ベイズの定理
最後にベイズの定理を紹介します。
全事象 \( \Omega \) を互いに排反な \( n \) 個の事象 \( B_1,B_2,\cdots,B_n \) に分割する。つまり、
$$ B_i\cap B_j=\emptyset \ (i\not=j), \quad B_1\cup B_2\cup \cdots \cup B_n=\Omega $$
このとき、 \( P(A)>0 \) となる任意の事象 \( A \) に対して、次が成り立つ。
$$ P(B_k|A)=\frac{P(B_k)P(A|B_k)}{\sum_{i=1}^nP(B_i)P(A|B_i)} \quad (k=1,2,\cdots,n) $$
定理2の証明(気になる方だけクリックしてください)
$$ \begin{align} P(B_k|A)&=\frac{P(B_k\cap A)}{P(A)} \quad (条件付き確率の定義より) \\ &=\frac{P(B_k)P(A|B_k)}{P(A)} \quad (定理1の確率の乗法公式より) \\ &=\frac{P(B_k)P(A|B_k)}{\sum_{i=1}^nP(B_i)P(A|B_i)} \quad (定理1の全確率の公式より) \end{align} $$
ベイズの定理の意味を理解するために、次の例を紹介します。
次は、ある工場の故障した場合の各設備の故障率と故障した場合における不良品が出る確率をまとめた表である。
ただし、2つ以上の設備が同時に故障することはないとする。
ここで、不良品が出る事象を \( A \) 、設備 \( i \) が故障する事象を \( B_i \) とおく。
| 各設備 | 故障した場合の各設備の故障率 \( P(B_i) \) | 故障した場合における不良品が出る確率 \( P(A|B_i) \) |
| 設備1 | 0.105 | 0.230 |
| 設備2 | 0.234 | 0.112 |
| 設備3 | 0.171 | 0.401 |
| 設備4 | 0.345 | 0.221 |
| 設備5 | 0.145 | 0.036 |
このとき、不良品が出た場合に設備 \( 2 \) の故障が原因である確率 \( P(B_2|A) \) を求める。
事象列 \( B_1,B_2,\cdots,B_5 \) は互いに排反で全事象 \( \Omega \) の分割であるので、ベイズの定理より、
$$ \begin{align} &P(B_2|A)=\frac{P(B_2)P(A|B_2)}{\sum_{i=1}^5P(B_i)P(A|B_i)} \\ &=\frac{0.234\times 0.112}{0.105\times 0.230+0.234\times 0.112+0.171\times 0.401+0.345\times 0.221+0.145\times 0.036} \\ &=\frac{0.0262}{0.2004}=0.1307 \end{align} $$
この例を見つつ、ベイズの定理の意味を考えてみましょう。
ある結果 \( A \) が起きる原因が \( B_1,B_2,\cdots,B_n \) となるような状況において何に興味があるかというと、結果 \( A \) が起きたときにその原因が \( B_i \) である確率 \( P(B_i|A) \) となります。
しかし、基本的に私たちが知ることができるのは、その原因 \( B_i \) が起きる確率 \( P(B_i) \) と原因が \( B_i \) のときの \( A \) が起きる確率 \( P(A|B_i) \) となります。
このとき、確率 \( P(B_i) \) を事前確率、確率 \( P(A|B_i) \) を事後確率といいます。
( \( A \) という結果を知る前と知った後の確率ということです。)
ベイズの定理というのは、事前確率と事後確率から、結果 \( A \) が起きたときにその原因が \( B_i \) である確率 \( P(B_i|A) \) を求める公式となっており、応用上とても重要な定理となっています。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

