こんにちは、ひかりです。
今回は確率・統計から変数の分類と量的データについて解説していきます。
この記事では以下のことを紹介します。
- 統計処理の流れについて
- 変数の分類について
- 度数分布表とヒストグラムについて
- 分布の特徴を表す指数について
- 5数要約と箱ひげ図について
統計処理の流れ
これから確率と統計について学んでいきますが、今自分が何のためにこの概念を勉強しているのかが分からなくなってしまうことがあります。
そのため、まずはじめに与えられたデータに対して、一連の統計処理の流れを見ていきましょう。
日本に住む小学一年生の平均身長が知りたいとする。
日本に住む小学一年生の平均身長が知りたいからといって、すべての小学一年生の身長のデータを集めようとすると、とてつもない時間と費用がかかります。
よって、一部の人に絞ってデータを集計します。
ただし、このとき偏りがないように選ぶ必要があります。
例えば、男子ばっかりから選んでいたのでは平均身長が高くなってしまいますし、東京の子ばっかり選んでは日本の平均身長を表しているとはいいがたいです。
与えられただけだとデータがごちゃごちゃしていてわかりにくいため、データの整理をしていきます。
例えば、身長が高い順に並べなおしたり、このデータ内での平均身長などを求めたりします。
見やすくなったデータをもとに、統計学の知識を用いて、いま知りたかった日本に住む小学一年生の平均身長を推測します。
また、推測した平均身長がどの程度信頼できるのかということまで調べることもできます。
この統計学の数学的基礎となるのが確率であるため、確率と統計は切っても切り離せない関係となっています。
まず、初めの4記事ほどでSTEP 2のデータの整理の仕方(記述統計)を学びます。
そのあと、STEP 3で必要となる確率の知識を一通り紹介した後に、(推測)統計学に入っていきます。
(推測)統計学のはじめに、STEP 1についても詳しく紹介する予定です。
変数の分類
調査や実験等で得られたデータの中で、個々のデータの対象のこと(Aさん、Bさん、A社、B社など)を個体またはケースといいます。
また、その個体に対して調査をした項目(テストの点、身長、社員数、資本金など)を変数といいます。
変数は以下のように分類することができます。
変数 | 質的変数 | (カテゴリーで示される) | 名義尺度 | (同じか違うかのみ意味をもつ) |
| 順序尺度 | (並び順に意味がある) | |||
量的変数 | (数値で示される) | 間隔尺度 | (並び順と2つの値の差に意味がある) | |
| 比例尺度 | (並び順・2つの値の差・比に意味があり、 原点0が意味を持つ) |
この表から見てわかるとおり、下の尺度に行くほど上位の尺度となります。
つまり、比例尺度は間隔尺度であり、順序尺度、名義尺度でもあります。
名義尺度:職業・好きな色・性別など
これらは何か数値で表されるものではなく、並び順にも意味をもたない。ただ、同じか違うかが重要である。
順序尺度:A~Fの成績評価・レースの順序など
これらも何か数値で表されるものではない。しかし、BよりAのほうが良い成績であるので、並び順には意味がある。
間隔尺度:気温・偏差値・テストの点など
これらは何℃、偏差値いくつ、何点などと数値で表現されるものである。並び順にも意味がある。
さらに、気温20℃が25℃になったら、気温は25-20=5℃上がったことになるので、2つの値の差に意味がある。
しかし、気温10℃と20℃では20℃の方が2倍暑いとはならないので、2つの比に意味をもたない。
よって、0に意味はない。たとえば、気温は摂氏℃、華氏℉などさまざま表し方があり、
$$ 0℃=32℉ $$
となるので、0は定め方の問題で特に意味をもたない。
ただし、絶対温度Kは比例尺度であることに注意。
比例尺度:身長・体重・速度など
これらは数値で表されていて、並び順・2つの値の差にも意味がある。
さらに、身長180cmの人は120cmの人より1.5倍大きいので、2つの値の比にも意味がある。
よって、0にも意味がある。たとえば、長さはcmのほかに、in(インチ)やyd(ヤード)などさまざま表し方があるが、
$$ 0\text{cm}=0\text{in}=0\text{yd} $$
となるので、0は基準となる重要な値である。
度数分布表とヒストグラム
ここからは、質的変数と量的変数に分けてデータの整理の仕方を紹介していきます。
今回の記事では量的変数のデータの整理の仕方を紹介します。(質的変数については次回)
まず、量的変数を用いたデータのことを量的データといいます。
この量的データを整理する方法として、度数分布表とヒストグラムがあります。
度数分布表
まずは、いろいろな言葉の定義をしていきます。
\( n \) 個の量的データの最大値と最小値の間をいくつかのグループ(階級)に分ける。
このとき、 \( i \) 番目の階級の中央の値 \( m_i \) をその階級の階級値という。
また、その階級に属するデータの個数 \( f_i \) を \( i \) 番目の階級の度数という。
これらをもとに次のような度数分布表を作成することができます。
| 階級 | 階級値 | 度数 |
| \( a_0 \ – \ a_1 \) | \( m_1=\frac{a_1-a_0}{2} \) | \( f_1 \) |
| \( a_1 \ – \ a_2 \) | \( m_2=\frac{a_2-a_1}{2} \) | \( f_2 \) |
| \( \vdots \) | \( \vdots \) | \( \vdots \) |
| \( a_{n-1} \ – \ a_n \) | \( m_n=\frac{a_n-a_{n-1}}{2} \) | \( f_n \) |
| 計 | \( n \) |
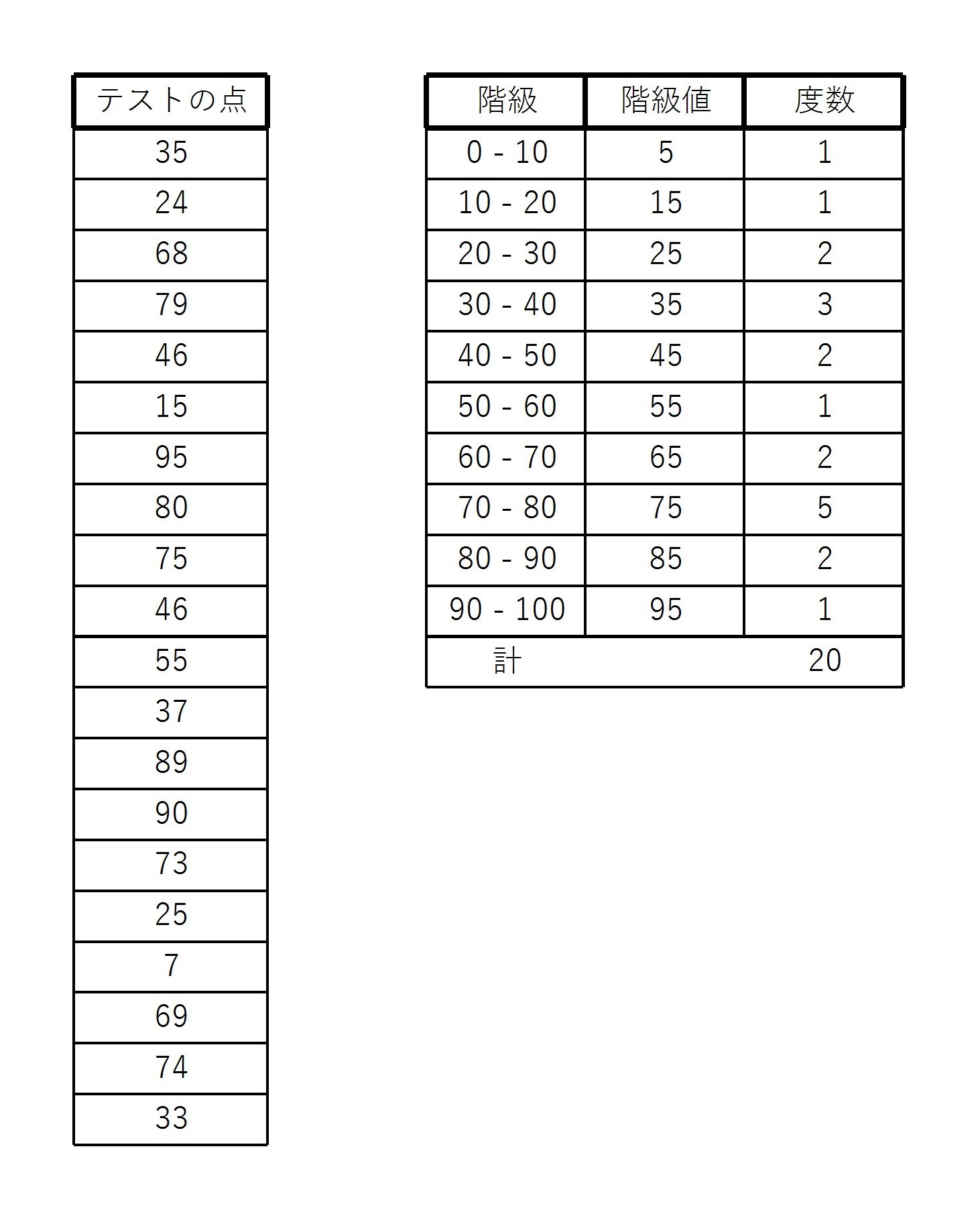
20人のテストの点が以下の図のように与えられたとする。
このとき、10点刻みに階級を設定すると、図のような度数分布表が書ける。
(80点は 70 – 80 の階級に90点は 80 – 90 の階級に入れてある)
さらに進んで、次を定義します。
はじめの階級から \( i \) 番目の階級までに含まれる度数の和
$$ f_1+f_2+\cdots+f_i $$
を累積度数という。
また、度数の総和に対する各階級の度数の割合 \( \frac{f_i}{n} \) を相対度数といい、はじめの階級から \( i \) 番目の階級までに含まれる相対度数の和
$$ \frac{f_1+f_2+\cdots+f_i}{n} $$
を累積相対度数という。
これらをもとに次のような累積相対度数分布表を作成することができます。
| 階級 | 度数 | 累積度数 | 相対度数 | 累積相対度数 |
| \( a_0 \ – \ a_1 \) | \( f_1 \) | \( f_1 \) | \( \frac{f_1}{n} \) | \( \frac{f_1}{n} \) |
| \( a_1 \ – \ a_2 \) | \( f_2 \) | \( f_1+f_2 \) | \( \frac{f_2}{n} \) | \( \frac{f_1}{n}+\frac{f_2}{n} \) |
| \( \vdots \) | \( \vdots \) | \( \vdots \) | \( \vdots \) | \( \vdots \) |
| \( a_{n-1} \ – \ a_n \) | \( f_n \) | \( \displaystyle \sum_{i=1}^nf_i \) | \( \frac{f_n}{n} \) | \( \displaystyle \sum_{i=1}^n\frac{f_i}{n} \) |
| 計 | \( n \) | \( 1 \) |
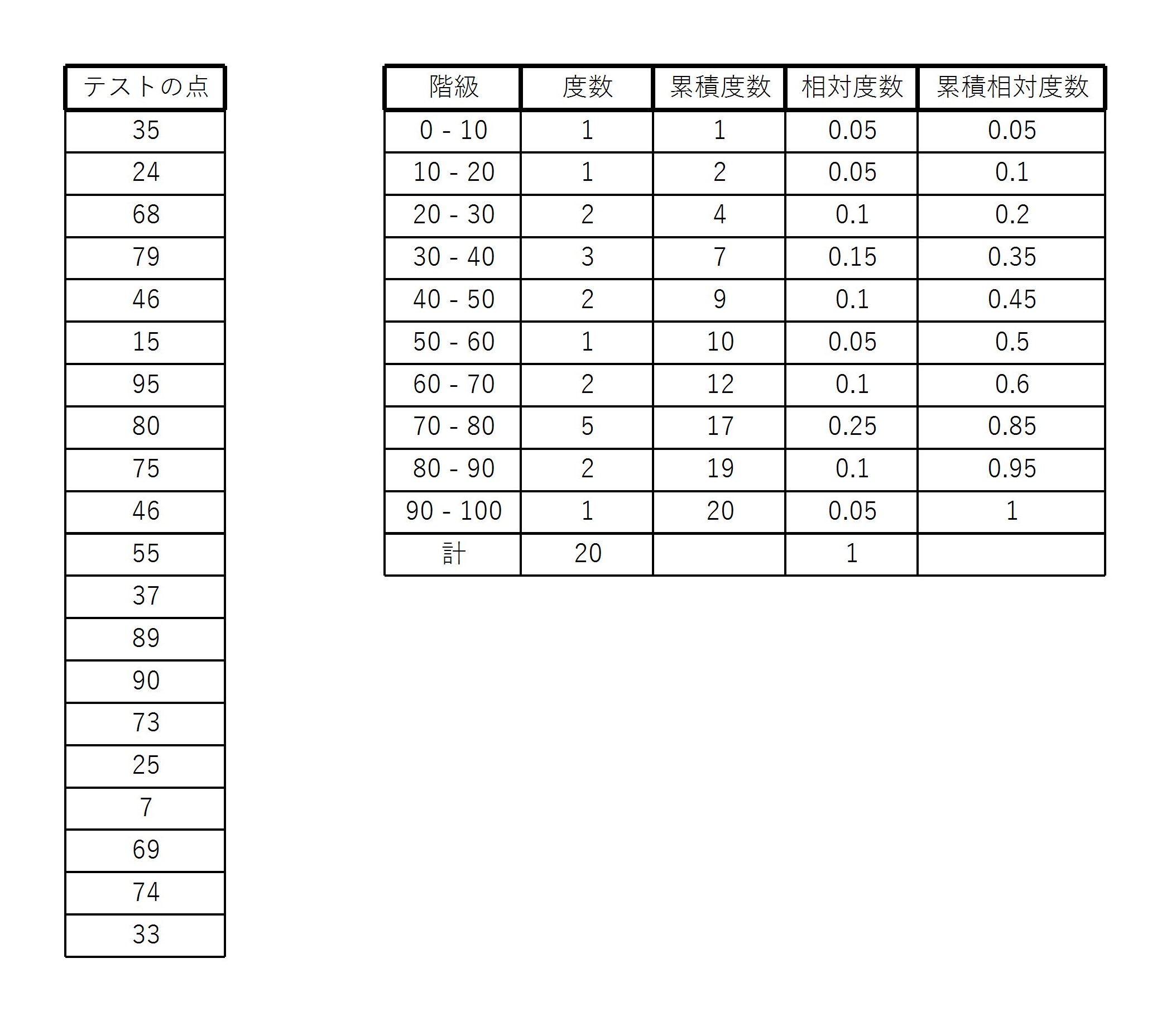
例3と同じ20人のテストの点を考える。
このとき、次のような累積相対度数表が書ける。
ヒストグラム
度数分布表からヒストグラムとよばれる柱状のグラフを作ることができます。
例3、例4と同じ20人のテストの点を考える。
このとき、例3の度数分布表をもとに次のようなヒストグラムが書ける。
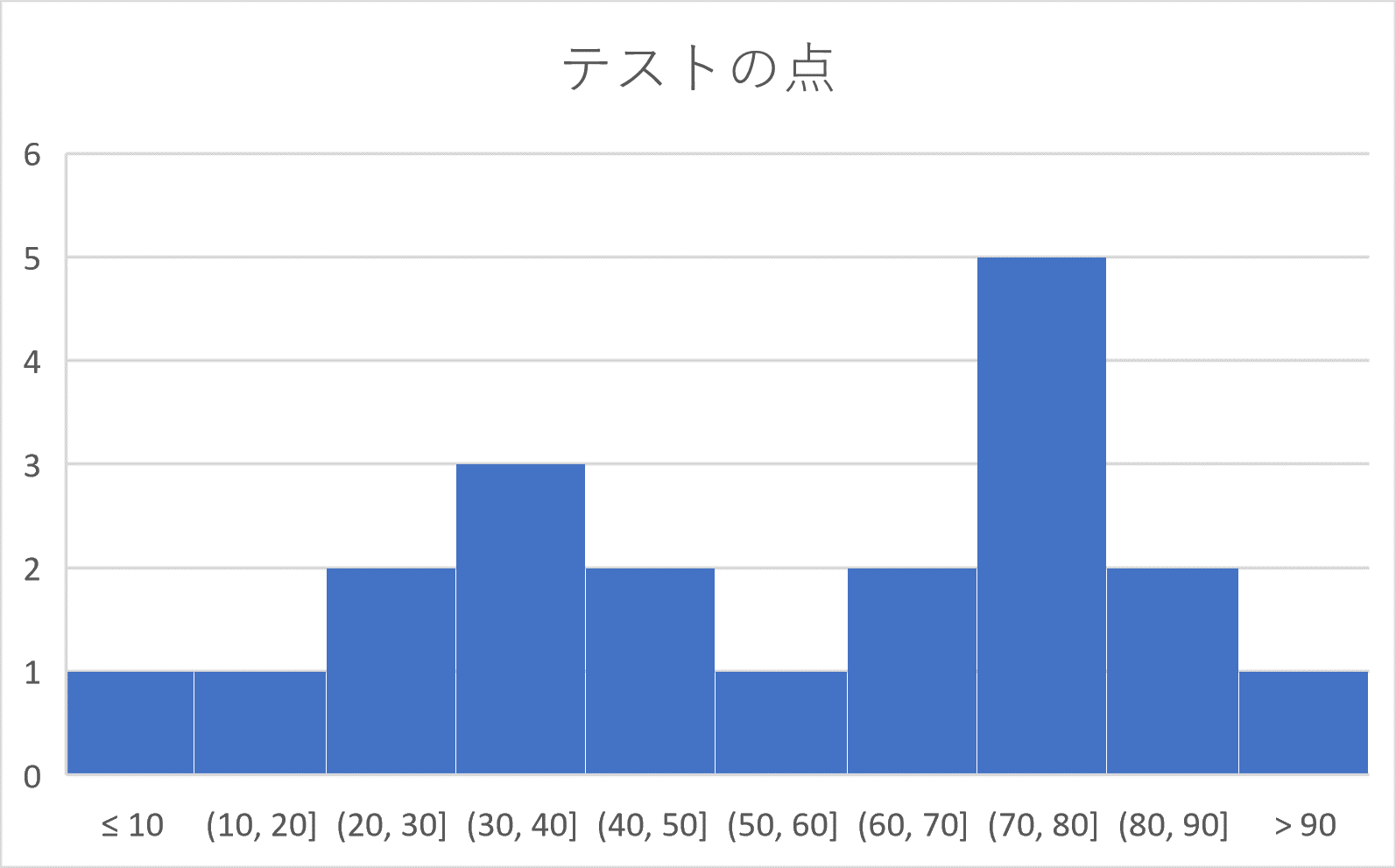
グラフの横軸が階級で、縦軸が度数を表している。
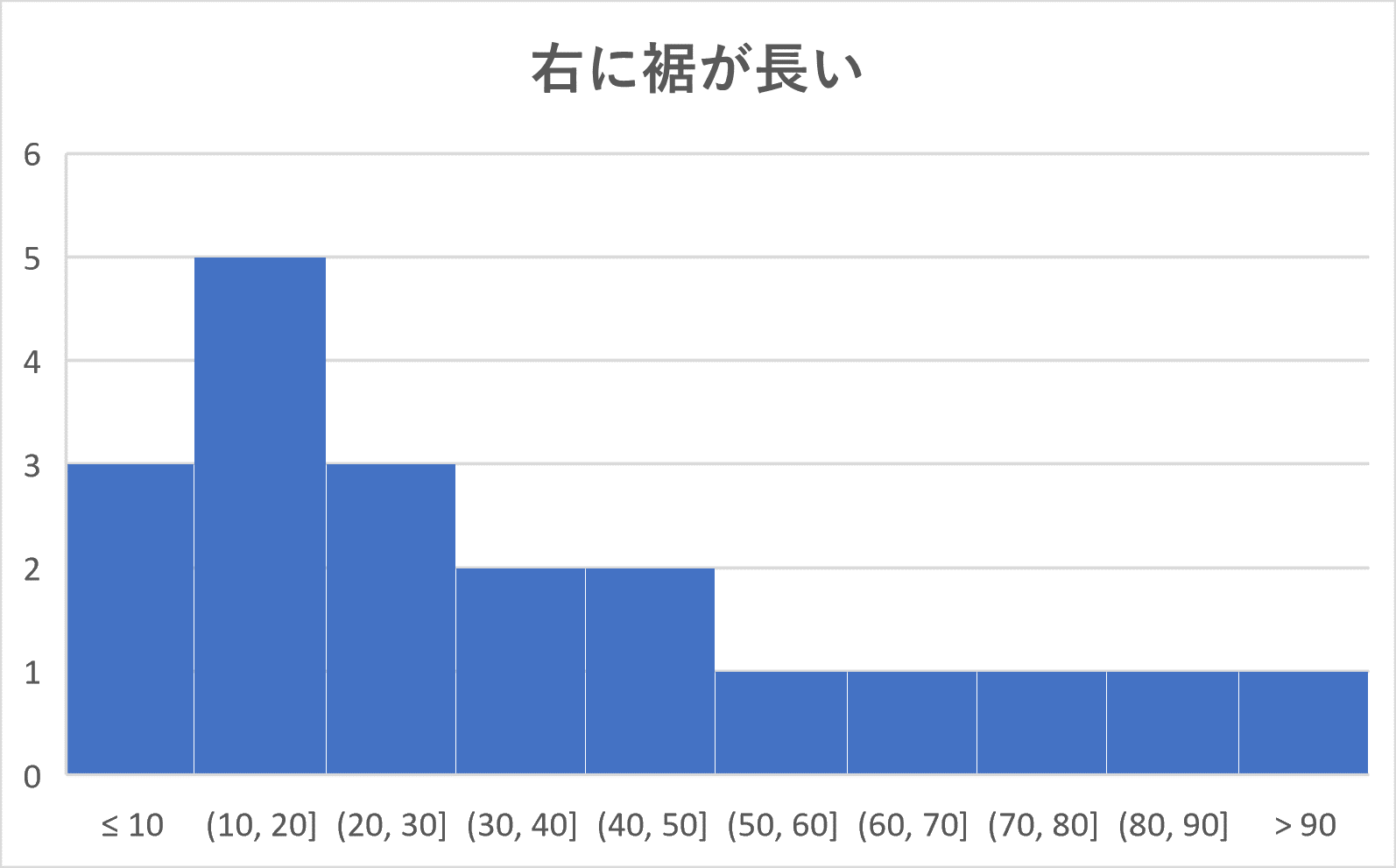
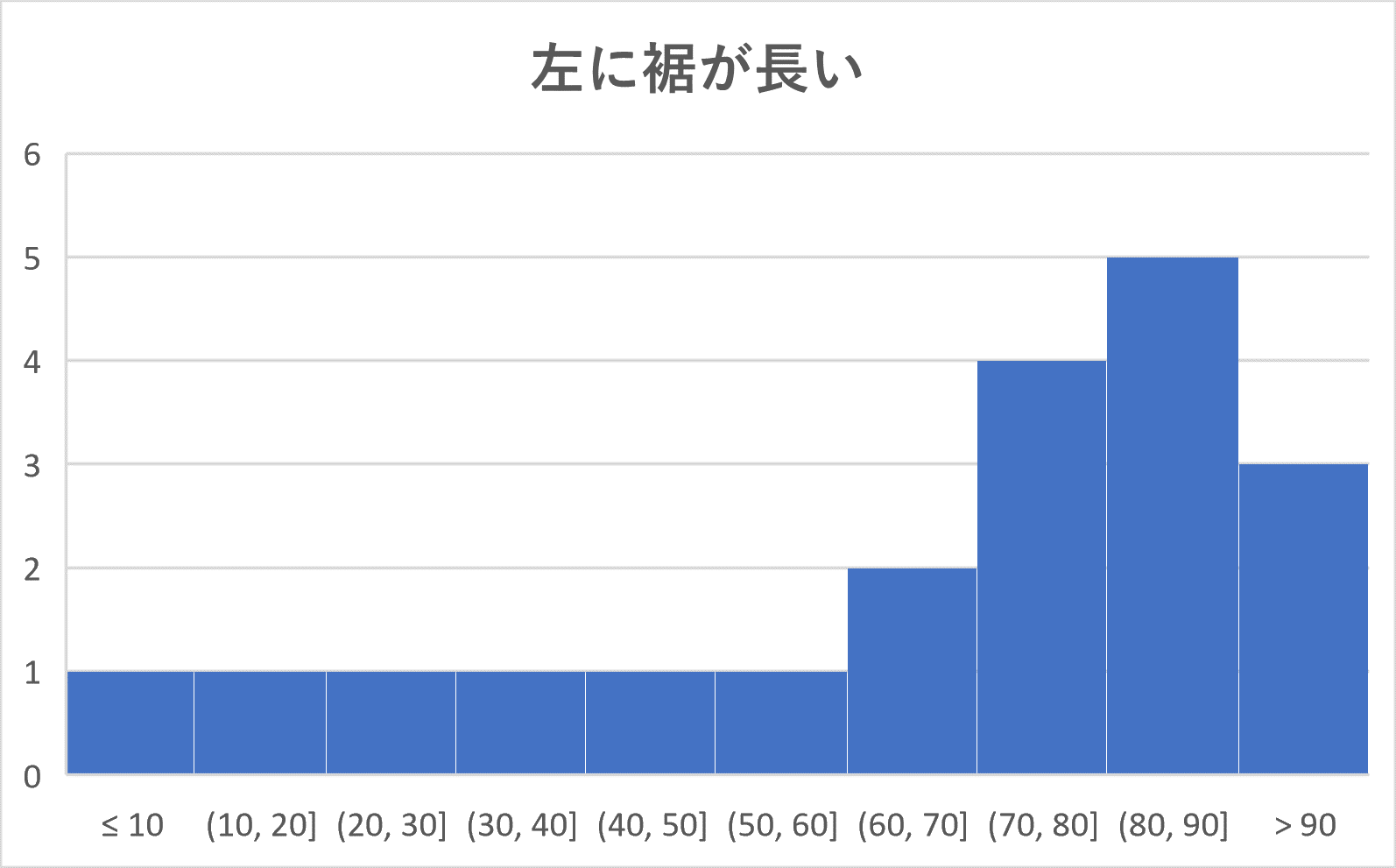
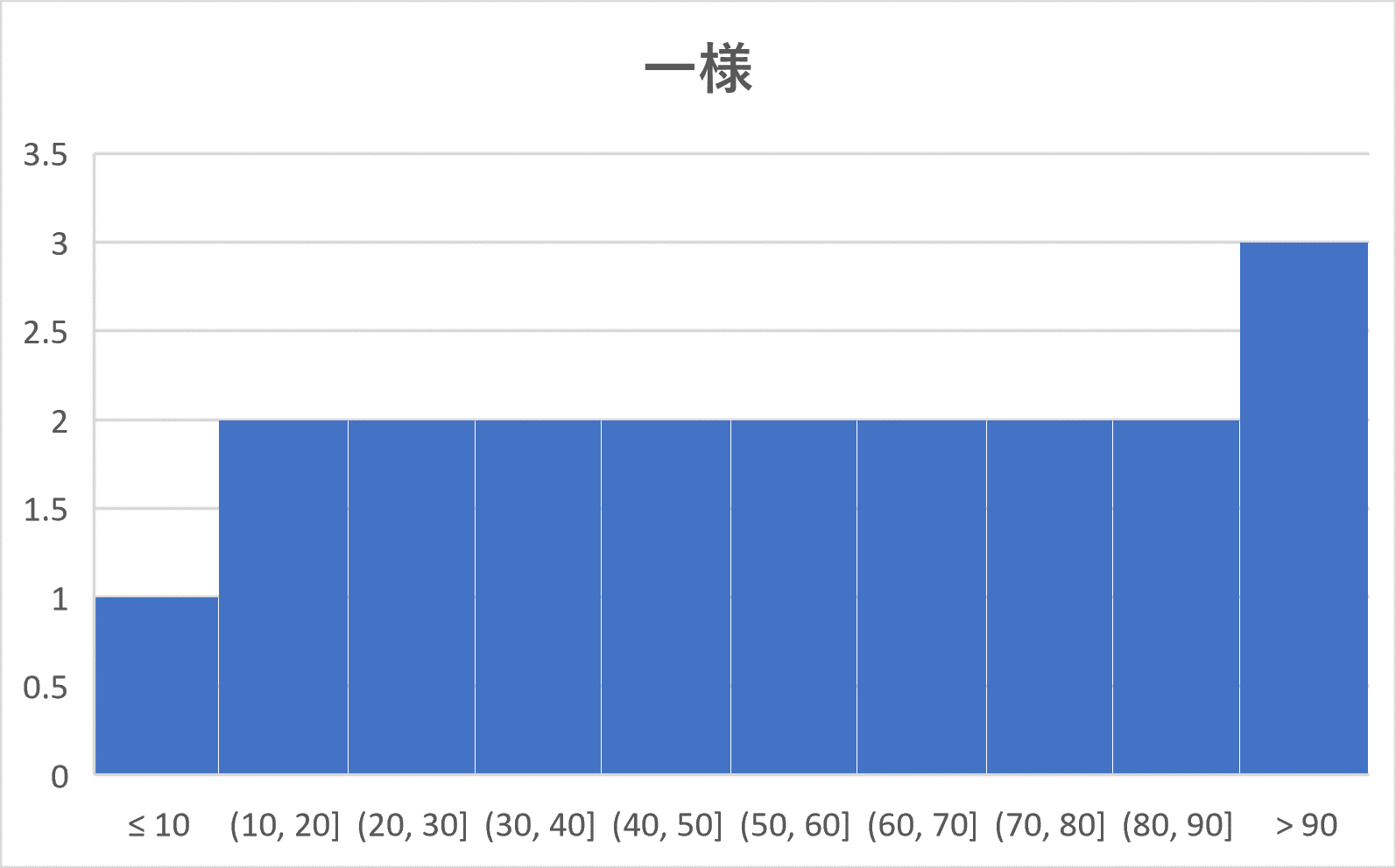
ヒストグラムを山のようにたとえて、その頂上にあたるところ(例5では 30 – 40 の階級と 70 – 80 の階級の部分)をそのヒストグラムの峰(みね)といいます。
このとき、峰が1つ(単峰)であるようなヒストグラムは次の4つのパターンに分かれます。
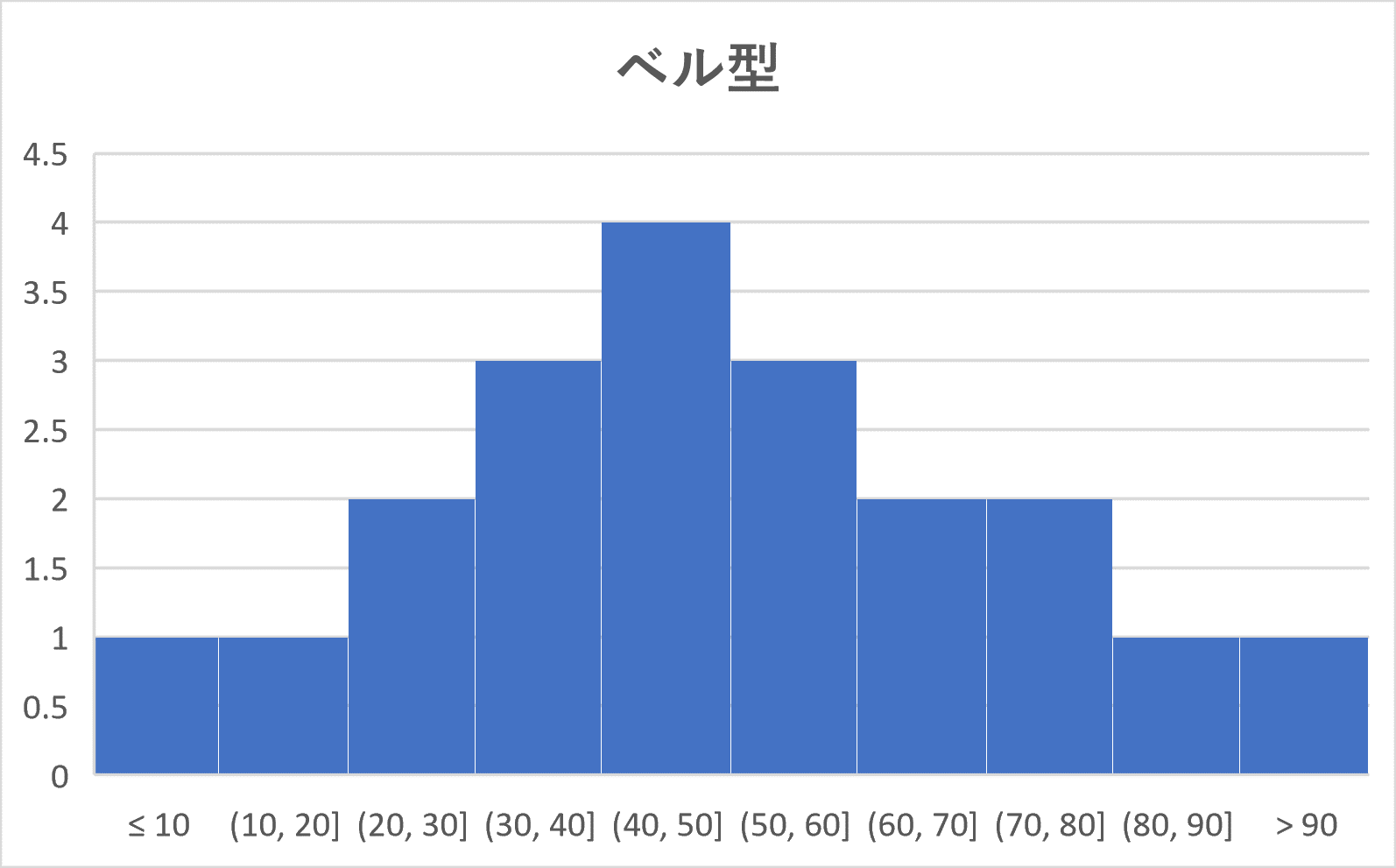
まとめると、
単峰のヒストグラムは次の4つのパターンに分類される。
(1) ベル型:ほぼ左右対称(ベルの形)となるような形
(2) 右に裾が長い:左に度数が集中していて、右に行くほど小さくなっていくような形
(3) 左に裾が長い:右に度数が集中していて、左に行くほど小さくなっていくような形
(4) 一様:あるところで、度数がほぼ同じような形
分布の特徴を表す指数
整理できたデータ全体を特徴づける1つの数値があると、統計をしていく際に便利になります。
データ全体の代表する位置を表す特性値を代表値といいます。
ここでは、代表値の例として、平均値・中央値・最頻値を紹介します。
また、データのばらつきを表す特性値を散布度といいます。
散布度の例として、分散・標準偏差・標準化得点・変動係数・範囲を紹介します。
平均値・分散・標準偏差
\( n \) 個のデータを
$$ x_1, \ x_2, \ \cdots, \ x_n $$
と表します。(例3の場合は \( n=20 \) )
このとき、データの中心を表す平均値を次のように定めます。
\( n \) 個のデータ \( x_1,x_2,\cdots,x_n \) に対して、平均値 \( \bar{x} \) を次で定める。
$$ \bar{x}=\frac{1}{n}(x_1+x_2+\cdots+x_n)=\frac{1}{n}\sum_{i=1}^nx_i $$
例3の20人のテストの点数の平均値を求める。

$$ \bar{x}=\frac{1}{20}\sum_{i=1}^nx_i=55.75 $$
であるので、平均値は55.75(点)となる。
続いて、データの平均値からの散らばり具合を表す分散と標準偏差を定義します。
\( n \) 個のデータ \( x_1,x_2,\cdots,x_n \) に対して、分散 \( s^2 \) を次で定める。
$$ s^2=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2 $$
ここで、 \( \bar{x} \) は \( n \) 個のデータの平均値である。
さらに、分散の正の平方根を標準偏差といい、 \( s \) で表す。つまり、
$$ s=\sqrt{s^2}=\sqrt{\frac{1}{n}\sum_{i=1}^n(x_1-\bar{x})^2} $$
なぜ、分散は \( x_i-\bar{x} \) を2乗するのでしょうか。
そもそも \( x_i-\bar{x} \) とは何かというと、平均値からデータがどれだけ離れているかを表したものとなっています。
しかし、 \( x_i-\bar{x} \) はデータによっては正にも負にもなります。
よって、これを \( i \) に関して足し合わせたものを分散と定義してしまうと、データが散らばっているにもかかわらず分散が小さくなってしまうことがあります。
(例えば、2つのデータ \( 10,20 \) があったとき平均値は \( 15 \) ですので、これらのデータは平均値から散らばっているわけですが、
$$ \frac{1}{2}\{ (x_1-\bar{x})+(x_2-\bar{x}) \}=\frac{1}{2}(-5+5)=0 $$
となり、分散が0となってしまいます。)
したがって、 \( x_i-\bar{x} \) を2乗してしまえば常に正となるので、正確にデータの散らばり具合が測れるということになります。
(ちなみに、絶対値を採用しないのは、場合分けが必要になったり微分ができなかったりといろいろと不便だからです。)
ただし、2乗することにより単位が変わってしまうので、単位をそろえるために標準偏差を導入します。
(たとえば、データの単位が \( \text{cm} \) だった場合、平均値の単位は同じ \( \text{cm} \) ですが、分散の単位は \( \text{cm}^2 \) となります。標準偏差は平方根をとるため、単位は \( \text{cm} \) に戻ります。)
標準偏差の見方としては、平均値 \( \pm \) 標準偏差の範囲に半分以上(正確には約68%)のデータが集中しているというふうに考えます。
例3の20人のテストの点数の分散と標準偏差を求める。

平均値は例6より、55.75(点)であった。よって、
$$ s^2=\frac{1}{20}\sum_{i=1}^n(x_i-55.75)^2=687.79 \quad (小数点第三位を四捨五入) $$
であるので、分散は687.79となる。
また、
$$ s=\sqrt{s^2}=26.23 \quad (小数点第三位を四捨五入) $$
であるので、標準偏差は26.23(点)となる。
したがって、半分以上の人が29.52(点)から81.98(点)の間の点数をとっているといえる。
標準化得点
次に、平均値と標準偏差が異なる2つのデータの集まりがあったときに、それぞれの平均値と標準偏差をそろえて比較しやすくする際によく用いられている標準化得点について紹介します。
\( n \) 個のデータ \( x_1,x_2,\cdots,x_n \) の平均値を \( \bar{x} \) 、標準偏差を \( s \) とする。
このとき、標準化得点(もしくは \( z \) 得点)を次で定める。
$$ x_iの標準化得点=\frac{x_i-\bar{x}}{s} \quad (i=1,2,\cdots,n) $$
各データ \( x_i \) を標準化得点を用いて変換すると、それらの集まりの平均値は \( 0 \) 、標準偏差は \( 1 \) になります。
これにより、複数個データの集まりがあったときにそれらの比較ができるようになります。
あるクラスの数学と物理のテストの平均点と標準偏差は次のようになった。
数学:平均点 \( 60 \) ・標準偏差 \( 5 \)
物理:平均点 \( 55 \) ・標準偏差 \( 20 \)
このとき、Aさんの数学と物理のテストの点数はそれぞれ \( 65 \) 点と \( 70 \) 点であった。
これだけだと、物理の方が数学より良い成績になるように見える。
しかし、それぞれの標準化得点を求めると、
$$ 数学の標準化得点=\frac{65-60}{5}=1 $$
$$ 物理の標準化得点=\frac{70-55}{20}=0.75 $$
となるので、数学の方が良い成績であることがいえる。
ここで、標準化得点の応用としてよく知られている指数の例を2つ紹介します。
(1) (偏差値)
高校受験や大学受験で嫌というほど聞いてきた偏差値は次のように求められる。
自分のテストの点を \( x \) とすると、
$$ 50+\frac{x-\bar{x}}{s}\times 10 $$
こうすることで、平均値が \( 50 \) 、標準偏差が \( 10 \) となる。
よって、偏差値は \( 40 \) から \( 60 \) の間に半分以上の人が入っている。
(2) (IQ(知能指数))
頭の良さを測るIQ(知能指数)は次のように求められる。
自分のIQテストの点を \( x \) とすると、
$$ 100+\frac{x-\bar{x}}{s}\times 15 \quad (ウェクスラー式) $$
こうすることで、平均値が \( 100 \) 、標準偏差が \( 15 \) となる。
よって、IQは \( 85 \) から \( 115 \) の間に半分以上の人が入っている。
変動係数
データ間の比較をする際に、場合によっては標準偏差が適切でない場合もあります。
このとき、別の指標が必要となります。
その候補として、変動係数というものがあり、次で定義されます。
データの平均値を \( \bar{x} \) 、標準偏差を \( s \) とするとき、変動係数 \( CV \) を次で定める。
$$ C=\frac{s}{\bar{x}} $$
スーパーにある2つの魚の値段の平均値と標準偏差は次で与えられるとする。
海老:平均値 \( 200 \) ・標準偏差 \( 50 \)
鯛:平均値 \( 1800 \) ・標準偏差 \( 300 \)
標準偏差だけをみると、鯛の値段の方が散らばっているように見える。
しかし、鯛の方が値段が高いので標準偏差もそれに応じて大きくなるのは当たり前である。
よって、標準偏差だけで散らばり具合を見るのは適切ではない。
そこで、変動係数を計算してみると、
$$ 海老の変動係数=\frac{50}{200}=0.25 $$
$$ 鯛の変動係数=\frac{300}{1800}=0.17 $$
よって、海老の方が散らばっていることがわかる。
中央値・最頻値
ヒストグラムがベル型のように左右対称に近い分布をしてるときは、平均値が代表値として有効に働きます。
しかし、そうでない場合は平均値が有効に働かない場合もあります。
たとえば、ニュースなどで日本人の平均年収や夏のボーナスの平均などを聞いて、みんなこんなにもらっているのかと驚いた方も多いと思います。
これは、年収やボーナスなどは上に上限がないため、左右対称の分布にならないからです。
そのさい、平均値の代わりに用いられる代表値として、中央値と最頻値があります。
(1) \( n \) 個のデータを小さい順にならべたとき、ちょうど真ん中にあるデータのことを中央値という。
ただし、 \( n \) が偶数のときは真ん中にあるデータは2つあるので、その2つのデータの平均値を中央値とする。
(2) \( n \) 個のデータのうち、もっとも頻度が多いデータのことを最頻値という。
また、ヒストグラムや度数分布表から最頻値を求める場合は度数が多い階級の階級値のことを(ヒストグラムの)最頻値という。
再び、例3の20人のテストの点数にもどり、中央値と最頻値を求める。
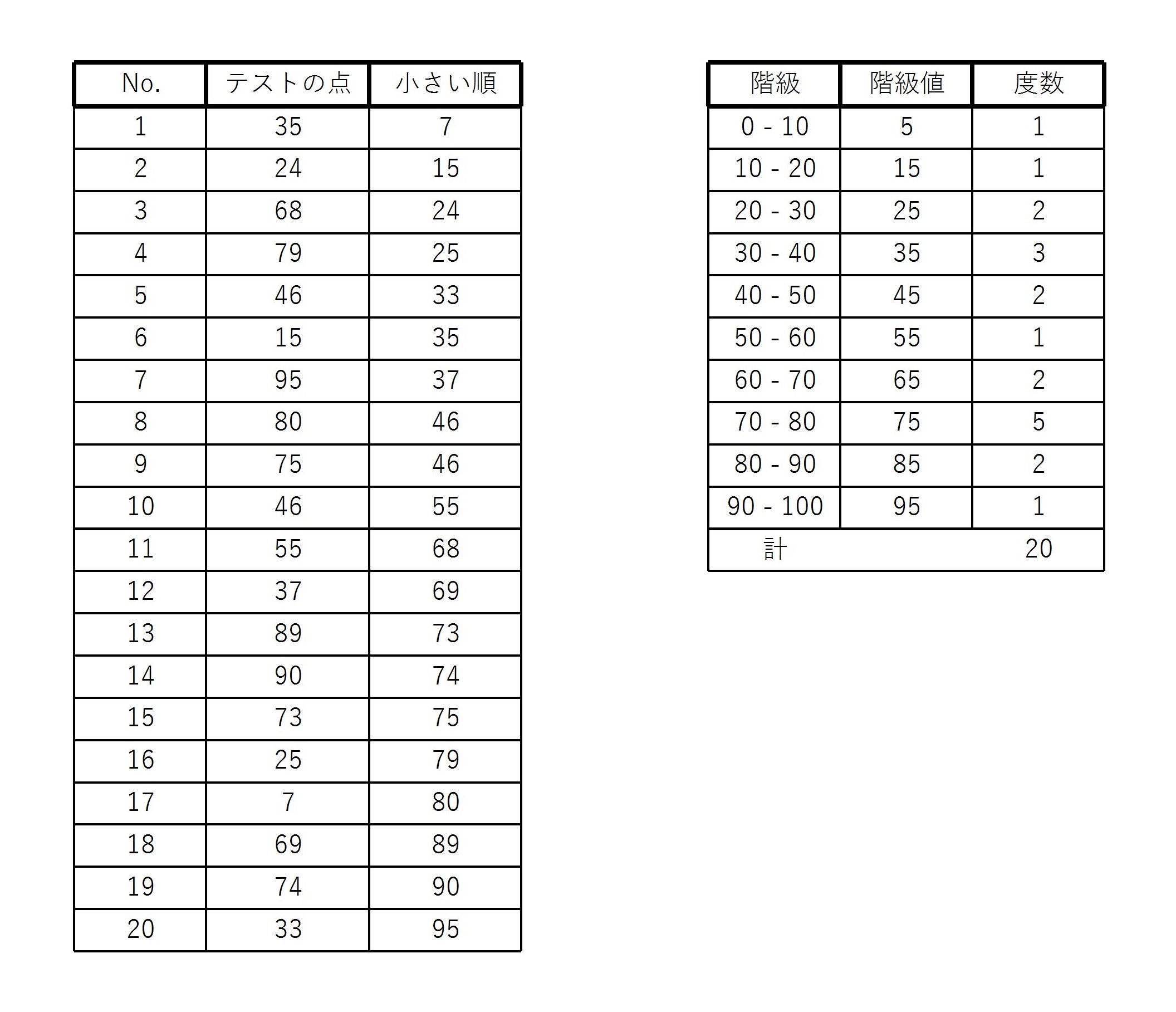
中央値はデータの数が \( 20 \) 個なので小さい順に並べたときの \( 10 \) 番目と \( 11 \) 番目の点の平均である。
\( 10 \) 番目は \( 55 \) 点、 \( 11 \) 番目は \( 68 \) 点であるので、中央値は
$$ \frac{55+68}{2}=61.5 $$
また、データを眺めると \( 46 \) 点を取った人が一番多いので、最頻値は \( 46 \) 点である。
この度数分布表から最頻値を求める場合は、 70 – 80 の階級がもっとも度数が多いため(ヒストグラムの)最頻値は \( 75 \) 点となる。
範囲・四分位数
また、散布度の指標として範囲というものもあります。
これは、いままでの散布度よりも計算はしやすいが、極端な値(外れ値)に影響を受けやすいものとなります。
データの最大値と最小値を用いて、範囲 \( R \) を次で定める。
$$ R=最大値-最小値 $$
例3の20人のテストの点数の範囲 \( R \) を求める。
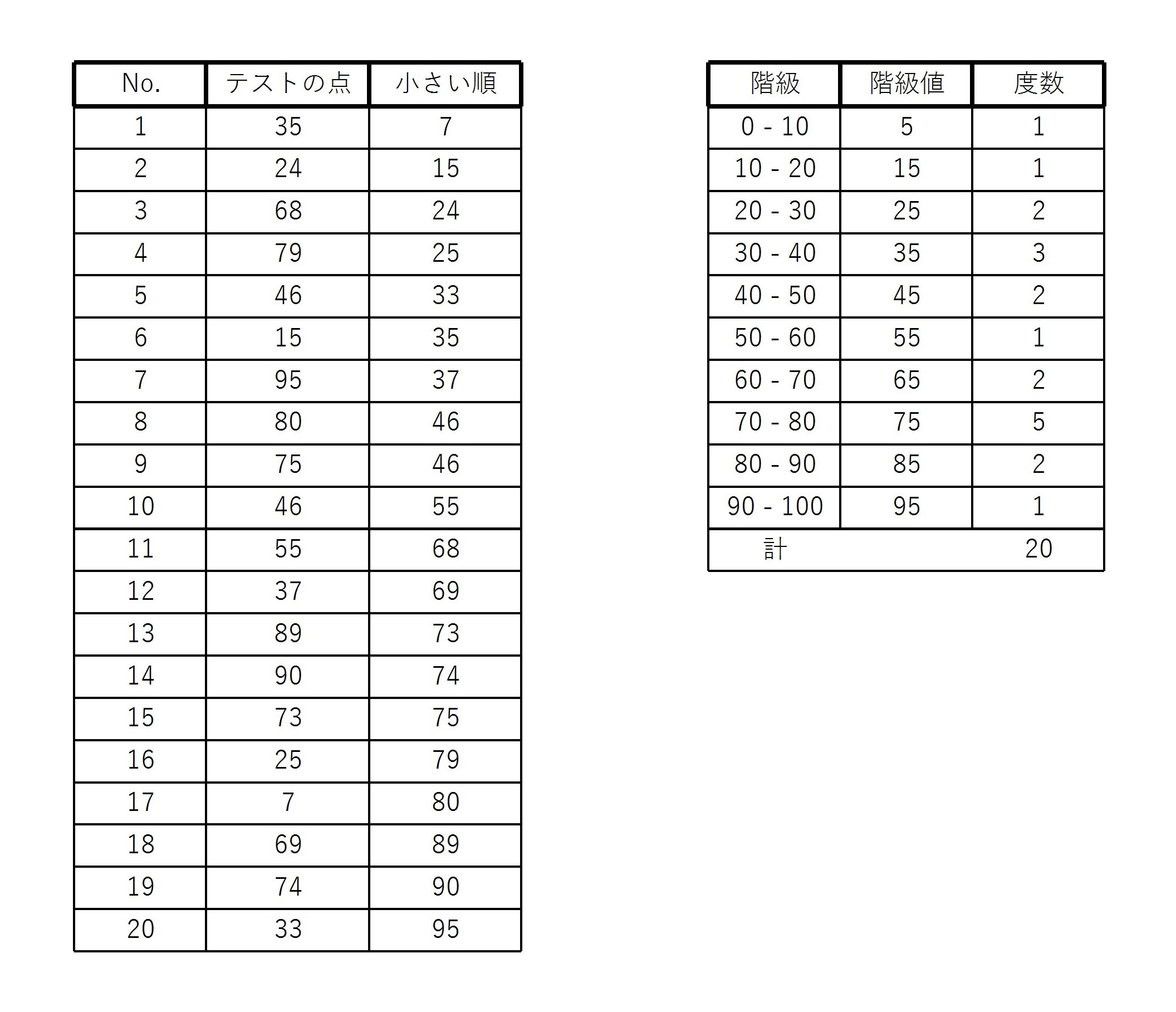
表より、
$$ R=95-7=88 $$
最後に、四分位数というものを定めます。
データを小さい順にならべたときに、4分の1ずつの場所にある値(25%点、50%点、75%点)をそれぞれ第1四分位数、第2四分位数、第3四分位数という。
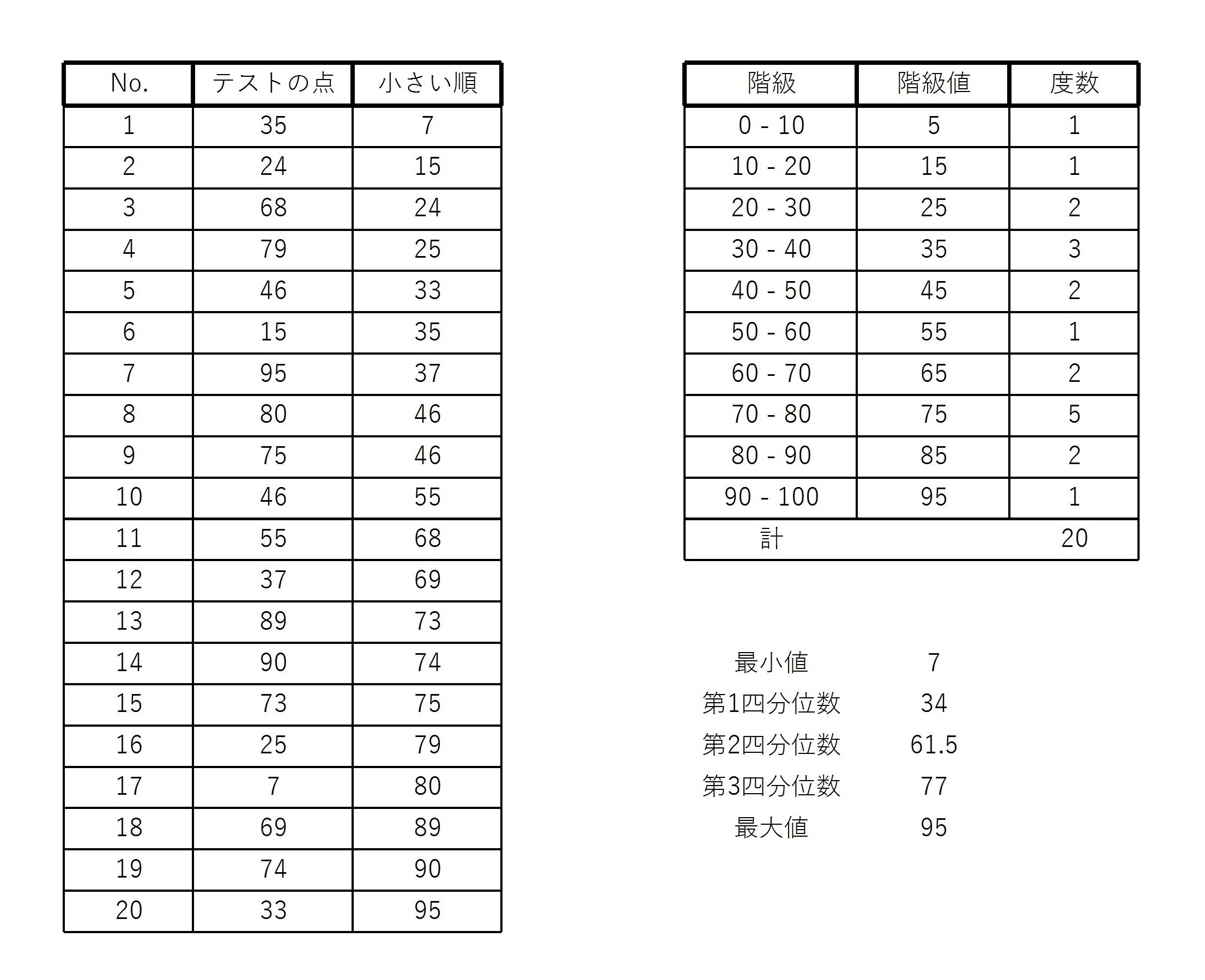
例3の20人のテストの点数の四分位数を求める。

第1四分位数は小さい順にならべたときの、 \( 5 \) 番目と \( 6 \) 番目の点の平均値である。
\( 5 \) 番目は \( 33 \) 点、 \( 6 \) 番目は \( 35 \) 点であるので、
$$ 第1四分位数=\frac{33+35}{2}=34 $$
第2四分位数は中央値のことなので、例11より \( 61.5 \) 点である。
第3四分位数は小さい順にならべたときの、 \( 15 \) 番目と \( 16 \) 番目の点の平均値である。
\( 15 \) 番目は \( 75 \) 点、 \( 16 \) 番目は \( 79 \) 点であるので、
$$ 第3四分位数=\frac{75+79}{2}=77 $$
5数要約と箱ひげ図
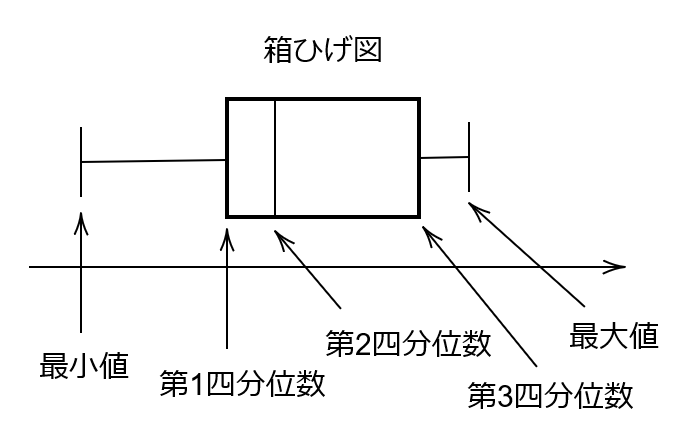
データをわかりやすく整理するグラフとして、ヒストグラムのほかに箱ひげ図があります。
箱ひげ図とは次に紹介する5数要約を用いて作成されます。
5数要約
5数要約とは次で定義されます。
データの最小値、第1四分位数、第2四分位数(中央値)、第3四分位数、最大値をあわせて5数という。
また、5数を表した表のことを5数要約という。
例3の20人のテストの点数の5数要約は次のようになる。
箱ひげ図
この5数要約を視覚的に表したものが箱ひげ図です。
次のようなグラフを箱ひげ図という。
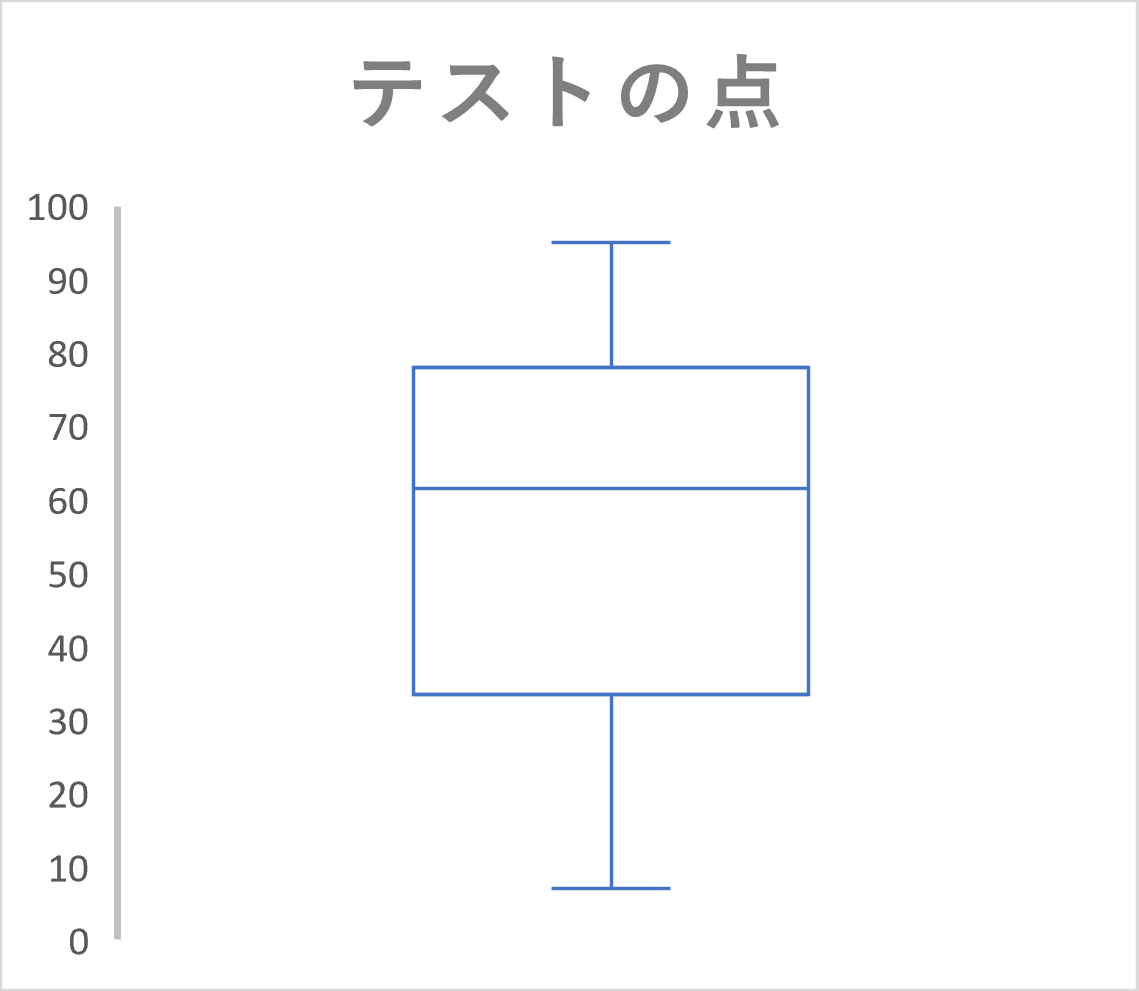
例3の20人のテストの点数の箱ひげ図は次のように書ける。

今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

