こんにちは、ひかりです。
今回は高校数学から定積分と区分求積法について解説していきます。
不定積分については前回の記事をご覧ください。
この記事では以下のことを紹介します。
- 定積分とその性質について
- 定積分の置換積分法と部分積分法について
- 定積分と面積の関係について
- 区分求積法について
定積分の定義と性質
定積分の定義
関数 \( f(x) \) の原始関数を \( F(x) \) とするとき、差 \( F(b)-F(a) \) を \( f(x) \) の \( a \) から \( b \) までの定積分といい、 \( \displaystyle \int_a^bf(x)dx \) と表します。
\( a \) をこの定積分の下端、 \( b \) を上端といいます。
また、 \( F(b)-F(a) \) を \( \displaystyle [F(x)]^b_a \) と表します。
まとめると、次のようになります。
\( f(x) \) の原始関数の1つを \( F(x) \) とするとき、
$$ \int_a^bf(x)dx=[F(x)]^b_a=F(b)-F(a) $$
(1) \( \displaystyle \int_1^3x^2 dx \) を計算する。
$$ \int_1^3x^2dx=\left[\frac{1}{3}x^3\right]^3_1=\frac{1}{3}\times 3^3-\frac{1}{3}\times 1^3=\frac{26}{3} $$
(2) \( \displaystyle \int_0^3(x-2)^2 dx \) を計算する。
$$ \begin{align} \int_0^3(x-2)^2dx&=\int_0^3(x^2-4x+4)dx \\ &=\left[ \frac{1}{3}x^3-2x^2+4x \right]^3_0 \\ &=\left( \frac{1}{3}\times 3^3-2\times 3^2+4\times 3\right)-0 \\ &=9-18+12=3 \end{align} $$
(3) \( \displaystyle \int_0^{\pi}6\sin 3\theta d\theta \) を計算する。
$$ (\cos 3\theta)’=-\sin3\theta\cdot (3\theta)’=-3\sin3\theta $$
より、
$$ \begin{align} \int_0^{\pi}6\sin 3\theta d\theta&=[-2\cos 3\theta]^{\pi}_0 \\ &=-2\cos 3\pi-(-2\cos 0)=4 \end{align} $$
定積分の性質
定積分の性質について、次が成り立ちます。(1)~(3)は不定積分の性質と同様です。
(1) $$ \int_a^bkf(x)dx=k\int_a^bf(x)dx \quad (k:定数) $$
(2) $$ \int_a^b\{ f(x)+g(x) \} dx=\int_a^bf(x)dx+\int_a^bg(x)dx $$
(3) $$ \int_a^b\{ f(x)-g(x) \} dx=\int_a^bf(x)dx-\int_a^bg(x)dx $$
(4) $$ \int_a^af(x)dx=0 $$
(5) $$ \int_b^af(x)dx=-\int_a^bf(x)dx $$
(6) $$ \int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx $$
定理1の証明(気になる方だけクリックしてください)
(6)を示す。
(6) $$ \begin{align} \int_a^cf(x)dx+\int_c^bf(x)dx&=[F(x)]^c_a+[F(x)]^b_c \\ &=\{F(c)-F(a)\}+\{F(b)-F(c)\} \\ &=F(b)-F(a)=\int_a^bf(x)dx \end{align} $$
(1) \( \displaystyle \int_{-1}^2(6x-x^2)dx+2\int_{-1}^2(x^2-3x)dx \) を計算する。
$$ \begin{align} &\int_{-1}^2(6x-x^2)dx+2\int_{-1}^2(x^2-3x)dx \\ &=\int_{-1}^2\{(6x-x^2)+2(x^2-3x)\}dx \\ &=\int_{-1}^2x^2dx=\left[ \frac{1}{3}x^3 \right]^2_{-1}=\frac{1}{3}\times 2^3-\frac{1}{3}\times(-1)^3=3 \end{align} $$
(2) \( \displaystyle \int_{-1}^2(2x-1)dx+\int_2^3(2x-1)dx \) を計算する。
$$ \begin{align} &\int_{-1}^2(2x-1)dx+\int_2^3(2x-1)dx \\ &=\int_{-1}^3(2x-1)dx=[x^2-x]^3_{-1}=4 \end{align} $$
(3) \( \displaystyle \int_0^{\frac{\pi}{6}}\sin 3x\cos 2xdx \) を計算する。
三角関数の和と積の公式より、
$$ \sin 3x\cos 2x=\frac{1}{2}(\sin 5x+\sin x) $$
となる。よって、
$$ \begin{align} &\int_0^{\frac{\pi}{6}}\sin 3x\cos 2xdx=\frac{1}{2}\int_0^{\frac{\pi}{6}}(\sin 5x+\sin x)dx \\ &=\frac{1}{2}\int_0^{\frac{\pi}{6}}\sin 5xdx+\frac{1}{2}\int_0^{\frac{\pi}{6}}\sin x dx \\ &=\frac{1}{2}\left[ -\frac{1}{5}\cos 5x \right]^{\frac{\pi}{6}}_0+\frac{1}{2}\left[ -\cos x \right]^{\frac{\pi}{6}}_0 \\ &=\frac{1}{2} \left\{ -\frac{1}{5}\cos \frac{5}{6}\pi-\left(-\frac{1}{5}\cos 0 \right)\right\}+\frac{1}{2}\left\{ -\cos\frac{\pi}{6}-\left( -\cos 0 \right)\right\} \\ &=\frac{\sqrt{3}}{20}+\frac{1}{10}-\frac{\sqrt{3}}{4}+\frac{1}{2}=\frac{3-\sqrt{3}}{5} \end{align} $$
定積分の置換積分法と部分積分法
定積分の置換積分法
前回の記事において、 \( x=g(t) \) のとき
$$ F(x)=F(g(t))=\int f(g(t))g'(t)dt \tag{1} $$
となることを学びました。
ここで、 \( x \) が \( a \) から \( b \) まで変わるとき、 \( t \) が \( \alpha \) から \( \beta \) まで変わるとします。
( \( x=g(t) \) なので、 \( x \) が \( a \) から \( b \) まで変わるとき、 \( t \) も \( a \) から \( b \) まで変わるとは限りません。)
このとき、
$$ \begin{align} \int_{\alpha}^{\beta}f(g(t))g'(t)dt&\overset{\text{(1)より}}{=}[F(g(t))]^{\beta}_{\alpha}=F(g(\beta))-F(g(\alpha)) \\ &=F(b)-F(a)=\int_a^bf(x)dx \end{align} $$
よって、次が成り立ちます。
\( x=g(t) \) とおくとき、 \( a=g(\alpha), \ b=g(\beta) \) ならば、
$$ \int_a^bf(x)dx=\int_{\alpha}^{\beta}f(g(t))g'(t)dt $$
\( \displaystyle \int_0^2\sqrt{3-x}dx \) を計算する。
\( \sqrt{3-x}=t \) とおくと、 \( x=3-t^2 \) より、 \( \frac{dx}{dt}=-2t, \ (dx=-2tdt) \)
よって、
| \( x \) | \( 0 \quad \to \quad 2 \) |
| \( t \) | \( \sqrt{3} \quad \to \quad 1 \) |
したがって、
$$ \begin{align} \int_0^2\sqrt{3-x}dx&=\int_{\sqrt{3}}^1t(-2tdt)=-2\int_{\sqrt{3}}^1t^2dt \\ &=-2\left[ \frac{1}{3}t^3 \right]^1_{\sqrt{3}}=-2\left( \frac{1}{3}\times 1^3-\frac{1}{3}\times (\sqrt{3})^3 \right) \\ &=-2\left( \frac{1}{3}-\sqrt{3}\right)=\frac{6\sqrt{3}-2}{3} \end{align} $$
定積分の部分積分法
不定積分のときと同様にして、次が成り立ちます。
$$ \int_a^bf(x)g'(x)dx=[f(x)g(x)]^b_a-\int_a^bf'(x)g(x)dx $$
(1) \( \displaystyle \int_0^{\frac{\pi}{2}}x\sin xdx \) を計算する。
\( x\sin x=x\cdot (-\cos x)’ \) と考えると、
$$ \begin{align} \int_0^{\frac{\pi}{2}}x\sin xdx&=\int_0^{\frac{\pi}{2}}x\cdot (-\cos x)’dx \\ &=[x\cdot (-\cos x)]^{\frac{\pi}{2}}_0-\int_0^{\frac{\pi}{2}}1\cdot (-\cos x)dx \\ &=[-x\cos x]^{\frac{\pi}{2}}_0+[\sin x]^{\frac{\pi}{2}}_0 \\ &=\left(-\frac{\pi}{2}\cos\frac{\pi}{2}-0 \right)+\left( \sin \frac{\pi}{2}-\sin 0\right)=1 \end{align} $$
(2) \( \displaystyle \int_1^ex\log xdx \) を計算する。
\( x\log x=\log x\cdot \left( \frac{1}{2}x^2 \right)’ \) と考えると、
$$ \begin{align} \int_1^ex\log xdx&=\int_1^e\log x\cdot \left( \frac{1}{2}x^2 \right)’dx \\ &=\left[ \frac{1}{2}x^2\log x \right]^e_1-\int_1^e\frac{1}{x}\cdot \left( \frac{1}{2}x^2 \right) dx \\ &=\left( \frac{1}{2}e^2\log e-\frac{1}{2}\cdot 1^2\cdot \log 1 \right)-\frac{1}{2}\int_1^exdx \\ &=\frac{1}{2}e^2-\frac{1}{2}\left[ \frac{1}{2}x^2 \right]^e_1 \\ &=\frac{1}{2}e^2-\frac{1}{2}\left( \frac{1}{2}e^2-\frac{1}{2} \right)=\frac{e^2+1}{4} \end{align} $$
定積分と面積の関係
区間 \( a≦ x≦ b \) において \( f(x)≧ 0 \) とし、 \( y=f(x) \) と \( x \) 軸の間にある図形の \( x \) 座標が \( a \) から \( x \) までの部分の面積を \( S(x) \) とおきます。
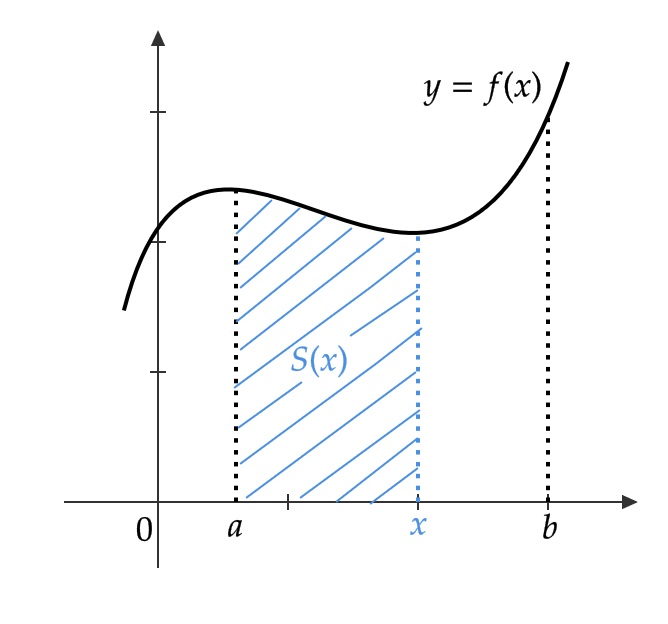
このとき、 \( S(x) \) の変化量 \( S(x+h)-S(x) \) は、 \( h>0 \) において区間 \( [x,x+h] \) の \( y=f(x) \) と \( x \) 軸の間にある図形の面積となります。
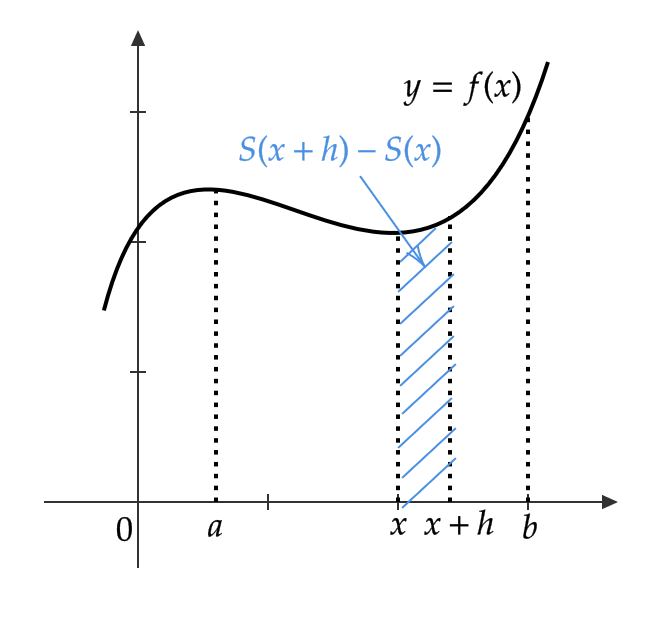
ここで、 \( S(x+h)-S(x)=hf(t) \) となる \( t \) をとります。
つまり、 \( S(x+h)-S(x) \) がよこ \( h \) 、たて \( f(t) \) の長方形の面積と等しくなる \( t \) を選びます。
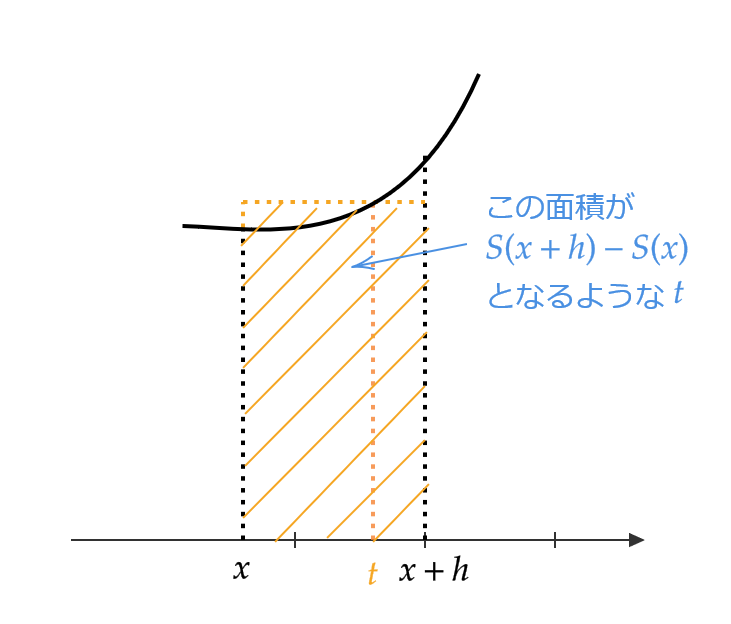
すると、
$$ \frac{S(x+h)-S(x)}{h}=f(t) $$
両辺に \( \displaystyle \lim_{h\to0} \) をとると、 \( h\to 0 \) のとき \( t\to x \) となるので、
$$ \lim_{h\to0}\frac{S(x+h)-S(x)}{h}=\lim_{h\to0}f(t)=\lim_{t\to x}f(t)=f(x) $$
よって、 \( S'(x)=f(x) \) となります。
つまり、 \( S(x) \) は \( f(x) \) の原始関数となります。
\( f(x) \) の原始関数を \( F(x) \) とおくと、前回の記事の一番初めの議論により、2つの原始関数の関係は
$$ S(x)=F(x)+C \quad (C:定数) \tag{2} $$
(2)で \( x=a \) を代入すると、
$$ S(a)=F(a)+C $$
\( S(x) \) の定義より\( S(a)=0 \) であるので、 \( C=-F(a). \) よって、
$$ S(x)=F(x)+F(a) \tag{3} $$
(3)で \( x=b \) を代入すると、
$$ S(b)=F(b)-F(a)=\int_a^bf(x)dx $$
\( S(b) \) を改めて \( S \) とおくと、次が成り立ちます。
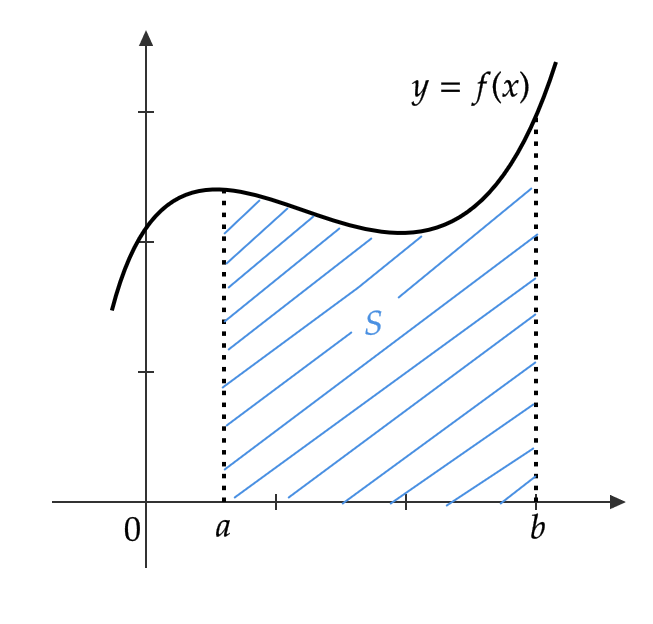
区間 \( a≦ x≦ b \) において、 \( f(x)≧ 0 \) とする。
曲線 \( y=f(x) \) と \( x \) 軸および \( x=a, \ x=b \) で囲まれた図形の面積 \( S \) は
$$ S=\int_a^bf(x)dx $$
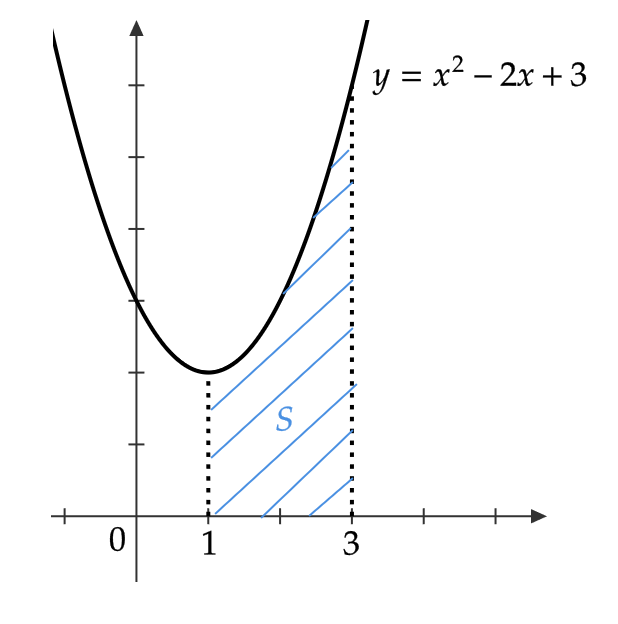
\( y=x^2-2x+3 \) と \( x \) 軸および \( x=1, \ x=3 \) で囲まれた図形の面積 \( S \) を求める。
$$ \begin{align} S&=\int_1^3(x^2-2x+3)dx \\ &=\left[ \frac{1}{3}x^3-x^2+3x \right]^3_1=\frac{20}{3} \end{align} $$
区分求積法
関数 \( f(x) \) が区間 \( [a,b] \) で連続で \( f(x)≧ 0\) とします。
区間 \( [a,b] \) を \( n \) 等分して、その点の座標を \( a \) に近い方から \( x_1,x_2,\cdots,x_{n-1} \) として、
$$ a=x_0, \ b=x_n, \ \frac{b-a}{n}=\Delta x $$
とおきます。( \( \frac{b-a}{n} \) は \( x_{i+1}-x_i \) の長さ)
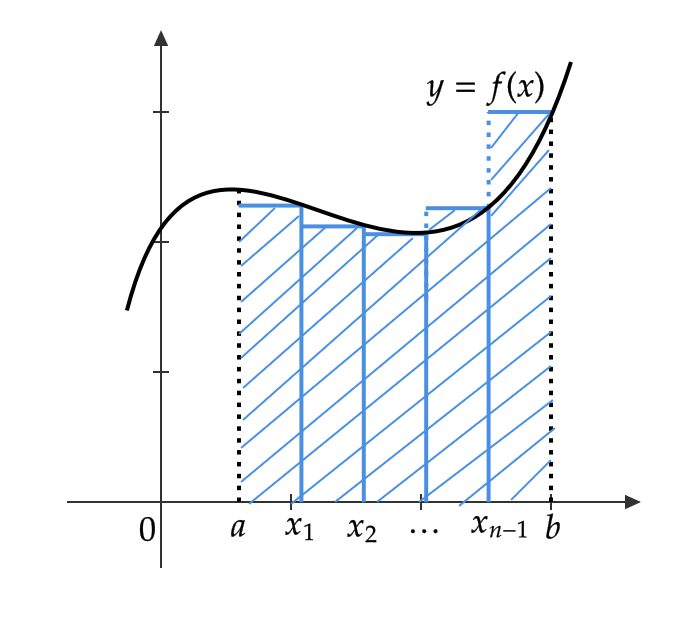
このとき、図のような \( n \) 個の長方形の面積の和
$$ S_n=f(x_1)\Delta x+f(x_2)\Delta x+\cdots+f(x_n)\Delta x=\sum_{k=1}^nf(x_k)\Delta x $$
は \( \displaystyle S=\int_a^bf(x)dx \) の近似値となります。
\( n\to\infty \) とすると、 \( [a,b] \) がどんどん細分化されていくので、 \( S \) に近づいていきます。
つまり、 \( \displaystyle \lim_{n\to\infty}S_n=S \)
よって、次が成り立ちます。
$$ \lim_{n\to\infty}\sum_{k=1}^nf(x_k)\Delta x=\int_a^bf(x)dx $$
ただし、 \( \Delta x=\frac{b-a}{n}, \ x_k=a+k\Delta x \)
このように、区間を細分化して和の極限として、面積や体積を求める方法を区分求積法といいます。
とくに、区間 \( [0,1] \) として区分求積法を考えてみましょう。
\( a=0, \ b=1, \ \Delta x=\frac{1}{n}, \ x_k=\frac{k}{n} \) とおくと、定理5より次が成り立ちます。
$$ \lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^nf\left( \frac{k}{n} \right)=\int_0^1f(x)dx $$
\( \displaystyle \lim_{n\to\infty}\frac{1}{n\sqrt{n}}(\sqrt{1}+\sqrt{2}+\cdots+\sqrt{n}) \) を求める。
$$ \begin{align} \frac{1}{n\sqrt{n}}(\sqrt{1}+\sqrt{2}+\cdots+\sqrt{n})&=\frac{1}{n}\left( \sqrt{\frac{1}{n}}+\sqrt{\frac{2}{n}}+\cdots \sqrt{\frac{n}{n}} \right) \\ &=\frac{1}{n}\sum_{k=1}^n\sqrt{\frac{k}{n}} \end{align} $$
よって、
$$ \lim_{n\to\infty}\frac{1}{n}\sum_{k=1}^n\sqrt{\frac{k}{n}}=\int_0^1\sqrt{x}dx=\left[ \frac{2}{3}\sqrt{x^3} \right]^1_0=\frac{2}{3} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

