こんにちは、ひかりです。
今回は高校数学から関数の極大・極小とグラフの概形について解説していきます。
関数の増減について知りたい方は前回の記事をご覧ください。
この記事では以下のことを紹介します。
- 関数の極大・極小について
- 関数のグラフの概形の書き方について
関数の極大・極小
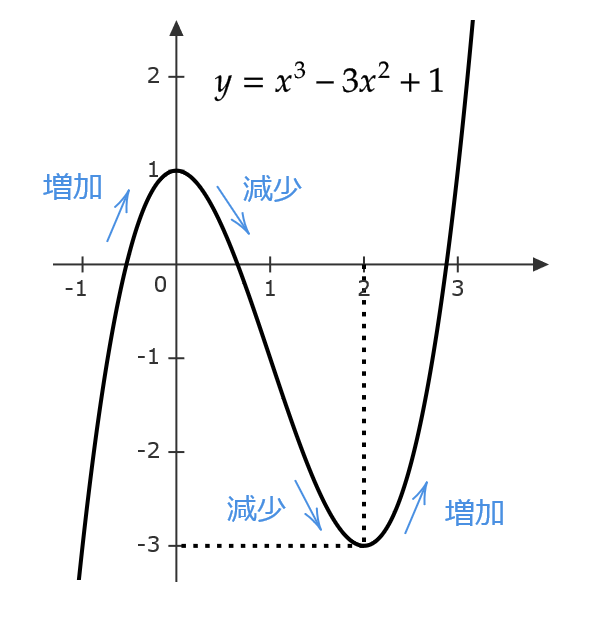
例として、 \( f(x)=x^3-3x^2+1 \) のグラフを考えてみましょう。
この関数は \( x=0 \) を境に増加から減少へと変わります。
このとき、 \( f(x) \) は \( x=0 \) で極大になるといい、そのときの \( f(x) \) の値 \( f(0)=1 \) を極大値といいます。
また、 \( x=2 \) を境に減少から増加へと変わります。
このとき、 \( f(x) \) は \( x=2 \) で極小になるといい、そのときの \( f(x) \) の値 \( f(2)=-3 \) を極小値といいます。
さらに、極大値と極小値を合わせて極値といいます。
きちんと定義すると、次のようになります。
関数 \( f(x) \) が \( x=a \) の近くで定義されていて、 \( x=a \) の十分近くでは \( x=a \) を除いて \( f(x)<f(a) \) となるとき、 \( f(x) \) は \( x=a \) において極大になるといい、 \( f(a) \) を極大値とよぶ。
同様に、 \( x=a \) の十分近くでは \( x=a \) を除いて \( f(x)>f(a) \) となるとき、 \( f(x) \) は \( x=a \) において極小になるといい、 \( f(a) \) を極小値とよぶ。
さらに、極大値と極小値を合わせて極値という。
ここで、次が成り立ちます。
関数 \( f(x) \) が \( x=a \) において微分可能であり、かつ \( x=a \) において極値をとるならば、 \( f'(a)=0 \)
よって、極大・極小の求め方は 次のようになります。
\( f'(a)=0 \) となる \( x=a \) を境にして
- \( f'(x) \) が正から負に変われば、 \( f(a) \) は極大値
- \( f'(x) \) が負から正に変われば、 \( f(a) \) は極小値
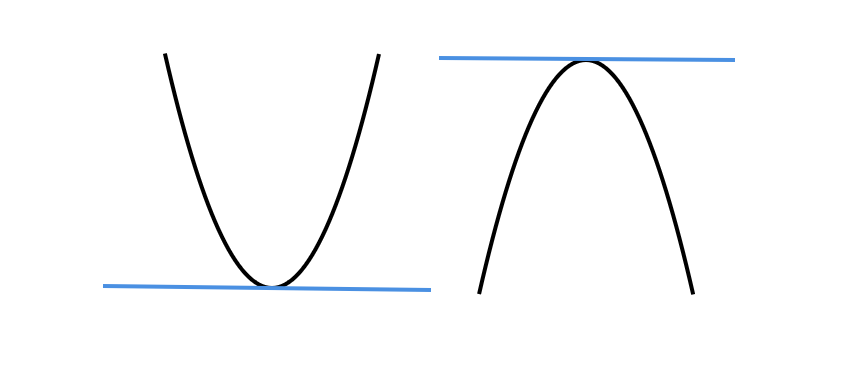
(1) \( f(x)=x^3-12x-1 \) の極値を求める。
\( f'(x)=3x^2-12=3(x+2)(x-2) \) より、 \( f'(x)=0 \) となる \( x \) は \( x=-2,2 \)
よって、 \( f(x) \) の増減表は次のようになる。
| \( x \) | \( \cdots \) | \( -2 \) | \( \cdots \) | \( 2 \) | \( \cdots \) |
| \( f'(x) \) | \( + \) | \( 0 \) | \( – \) | \( 0 \) | \( + \) |
| \( f(x) \) | \( \nearrow \) | \( 15 \) | \( \searrow \) | \( -17 \) | \( \nearrow \) |
したがって、
\( x=-2 \) のとき極大で、極大値 \( 15 \)
\( x=2 \) のとき極小で、極小値 \( -17 \)
(2) \( f(x)=\sin x(1+\cos x) \ (0≦ x≦ 2\pi) \) の極値を求める。
$$ \begin{align} f'(x)&=\cos x(1+\cos x)-\sin^2x \\ &=\cos x+\cos^2x-(1-\cos^2x) \\ &=2\cos^2x+\cos x-1=(2\cos x-1)(\cos x+1) \end{align} $$
より、 \( 0≦ x≦ 2\pi \) 上で \( f'(x)=0 \) となる \( x \) は \( \cos x=\frac{1}{2},-1 \) より、 \( x=\frac{\pi}{3},\pi,\frac{5}{3}\pi \)
よって、 \( f(x) \) の増減表は次のようになる。
| \( x \) | \( 0 \) | \( \cdots \) | \(\frac{\pi}{3} \) | \( \cdots \) | \( \pi \) | \( \cdots \) | \( \frac{5}{3}\pi \) | \( \cdots \) | \( 2\pi \) |
| \( f'(x) \) | \( + \) | \( 0 \) | \( – \) | \( 0 \) | \( – \) | \( 0 \) | \( + \) | ||
| \( f(x) \) | \( 0 \) | \( \nearrow \) | \( \frac{3\sqrt{3}}{4} \) | \( \searrow \) | \( 0 \) | \( \searrow \) | \( -\frac{3\sqrt{3}}{4} \) | \( \nearrow \) | \( 0 \) |
したがって、
\( x=\frac{\pi}{3} \) のとき極大で、極大値 \( \frac{3\sqrt{3}}{4} \)
\( x=\frac{5}{3}\pi \) のとき極小で、極小値 \( -\frac{3\sqrt{3}}{4} \)
関数のグラフの概形
曲線の凹凸
\( f'(x) \) の導関数を \( f^{\prime\prime}(x) \) と書いて、2階(2次)導関数といいます。(階はこの字であってます)
\( f^{\prime\prime}(x) \) が \( f(x) \) にどのような影響を与えるのかを見ていきましょう。
前回の記事の定理3を用いると、 \( f'(x) \) の値の増減は \( f^{\prime\prime}(x) \) の値の正負で判定できます。
すなわち、
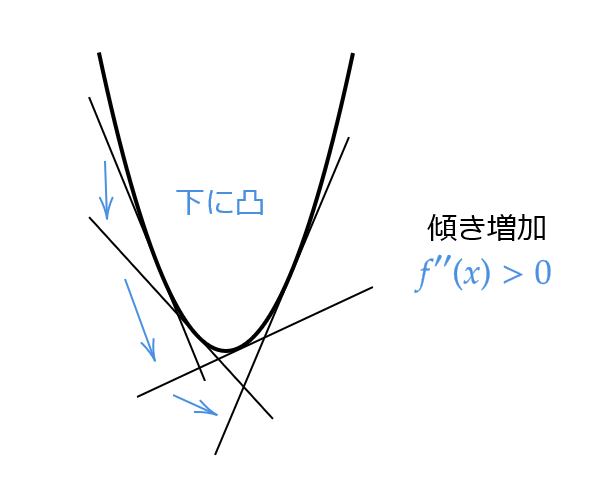
- \( f^{\prime\prime}(x)>0 \) となる区間では、\( f'(x) \) の値は増加する。つまり、 \( f(x) \) の接線の傾きが増加する。
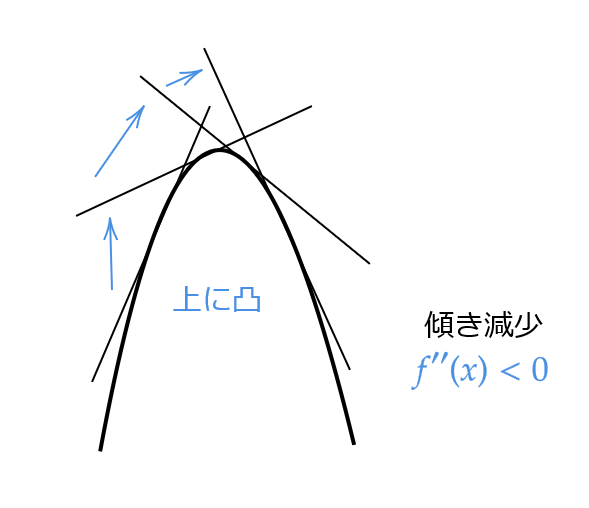
- \( f^{\prime\prime}(x)<0 \) となる区間では、\( f'(x) \) の値は減少する。つまり、 \( f(x) \) の接線の傾きが減少する。
よって、次が成り立ちます。
(1) \( f^{\prime\prime}(x)>0 \) となる区間では、曲線 \( y=f(x) \) は下に凸となる。
(2) \( f^{\prime\prime}(x)<0 \) となる区間では、曲線 \( y=f(x) \) は上に凸となる。
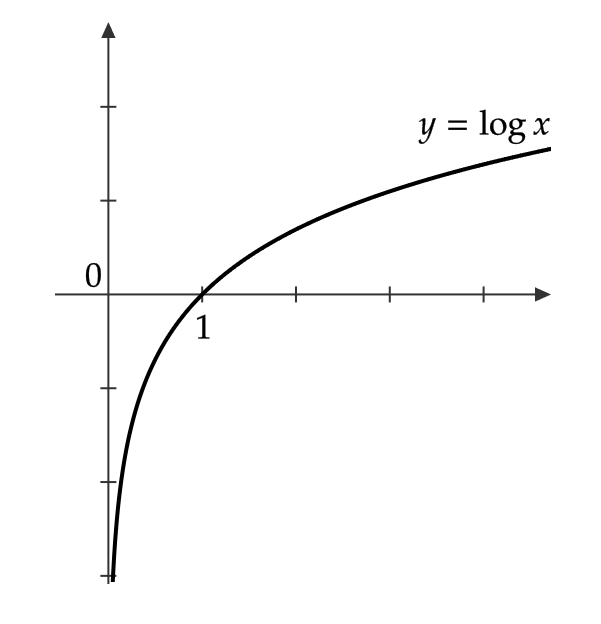
(1) \( y=\log x \) の凹凸を調べる。
\( y’=\frac{1}{x} \) より、 \( y^{\prime\prime}=-\frac{1}{x^2}<0 \)
よって、 \( y=\log x \) は \( x>0 \) で上に凸である。
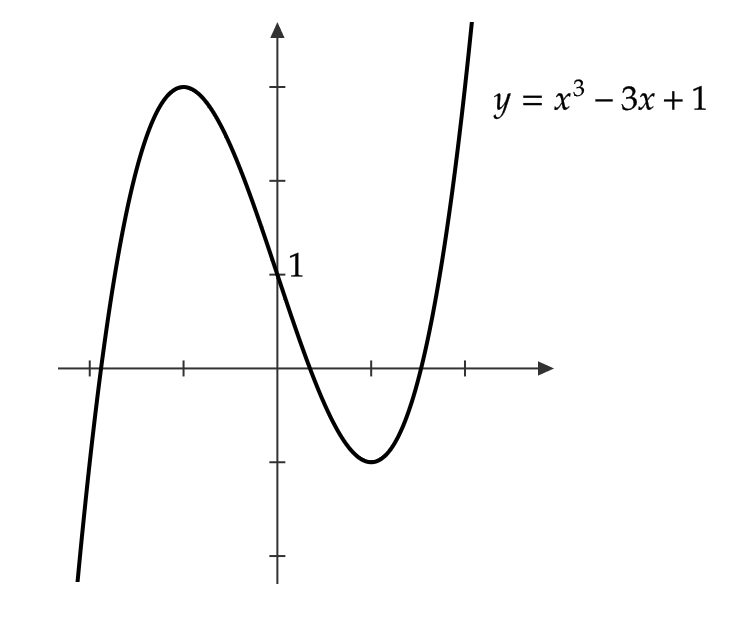
(2) \( y=x^3-3x+1 \) の凹凸を調べる。
\( y’=3x^2-3 \) より、 \( y^{\prime\prime}=6x \)
よって、
\( x<0 \) のとき \( y^{\prime\prime}<0 \) より、上に凸
\( x>0 \) のとき \( y^{\prime\prime}>0 \) より、下に凸
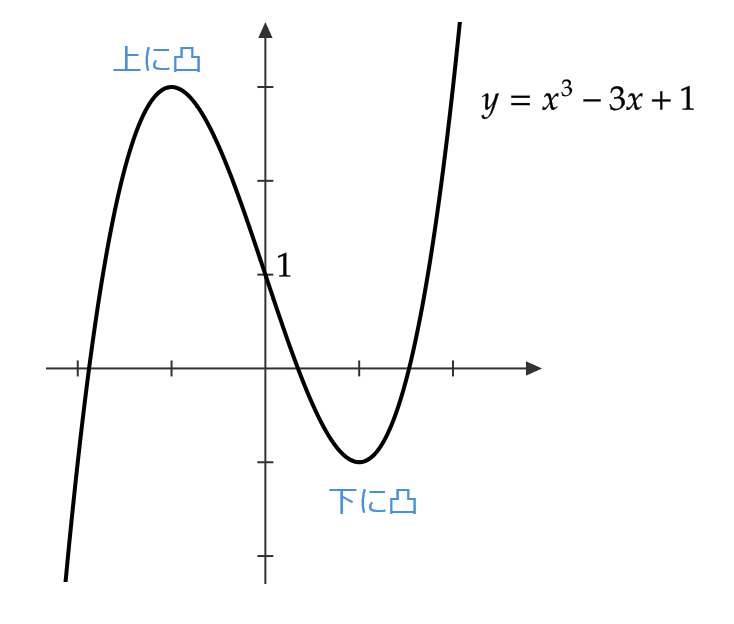
変曲点
例2 (2)の \( y=x^3-3x+1 \) では、点 \( (0,1) \) の左右で上に凸、下に凸が入れ替わることがわかります。
このように、曲線の凹凸が入れ替わる点を変曲点といいます。
変曲点に関して、一般に次が成り立ちます。
\( f(x) \) が2階微分可能であり、 \( f^{\prime\prime}(a)=0 \) であるとき、 \( x=a \) の前後で \( f^{\prime\prime}(x) \) の符号が変われば、曲線 \( y=f(x) \) 上の点 \( (a,f(a)) \) は変曲点である。
グラフの概形の書き方
前回と今回の内容を合わせると、関数のグラフの概形を書くことができます。
グラフを書く手順としては、次のようになります。
- \( y’, \ y^{\prime\prime} \) を求める。
- \( y’=0, \ y^{\prime\prime}=0 \) となる \( x \) を求める。
- 増減表を作る。
- 極大値・極小値・変曲点を求める。
- \( \displaystyle \lim_{x\to\infty}y, \ \lim_{x\to-\infty}y \) などを求める。
- それらをもとに、グラフを作成する。
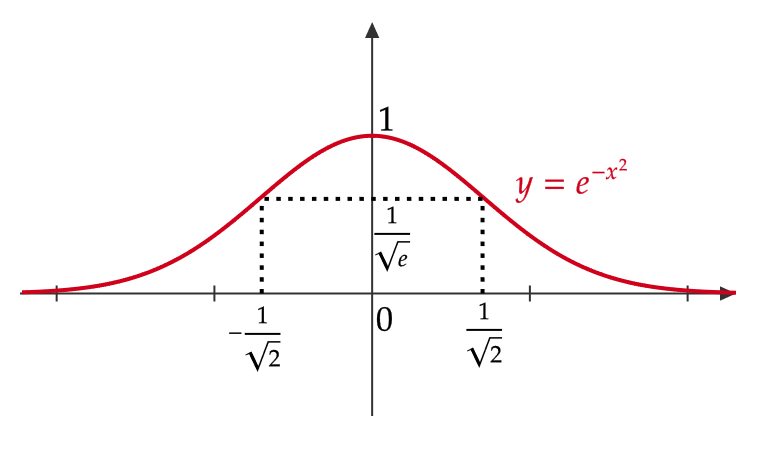
(1) 関数 \( y=e^{-x^2} \) の増減、極値、グラフの凹凸および変曲点を調べて、そのグラフを書いてみる。
\( y’=-2xe^{-x^2} , \ y^{\prime\prime}=2(2x^2-1)e^{-x^2} \) より、
\( y’=0 \) となる \( x \) は \( x=0 \)
\( y^{\prime\prime}=0 \) となる \( x \) は \( x=-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}} \)
よって、増減表をつくると、
| \( x \) | \( \cdots \) | \( -\frac{1}{\sqrt{2}} \) | \( \cdots \) | \( 0 \) | \( \cdots \) | \( \frac{1}{\sqrt{2}} \) | \( \cdots \) |
| \( y’ \) | \( + \) | \( + \) | \( + \) | \( 0 \) | \( – \) | \( – \) | \( – \) |
| \( y^{\prime\prime} \) | \( + \) | \( 0 \) | \( – \) | \( – \) | \( – \) | \( 0 \) | \( + \) |
| \( y \) | \( \color{red}{⤴} \) | \( \frac{1}{\sqrt{e}} \) | \( \color{red}{↱} \) | \( 1 \) | \( \color{red}{⤵} \) | \( \frac{1}{\sqrt{e}} \) | \( \color{red}{↳} \) |
( \( y \) が増加で下に凸のとき ⤴ 、増加で上に凸のとき ↱ (打てないので角ばっていますが本当は曲がった矢印)、減少で上に凸のとき ⤵ 、減少で下に凸のとき ↳ (打てないので角ばっていますが本当は曲がった矢印)と書きます。)
よって、 \( y \) は \( x=0 \) で極大で、極大値 \( 1 \)
極小値はない
また、変曲点は \( (-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{e}}), \ (\frac{1}{\sqrt{2}},\frac{1}{\sqrt{e}}) \)
さらに、 \( \displaystyle \lim_{x\to\infty}e^{-x^2}=0, \ \lim_{x\to-\infty}e^{-x^2}=0 \) である。
よって、グラフは次のように書くことができる。
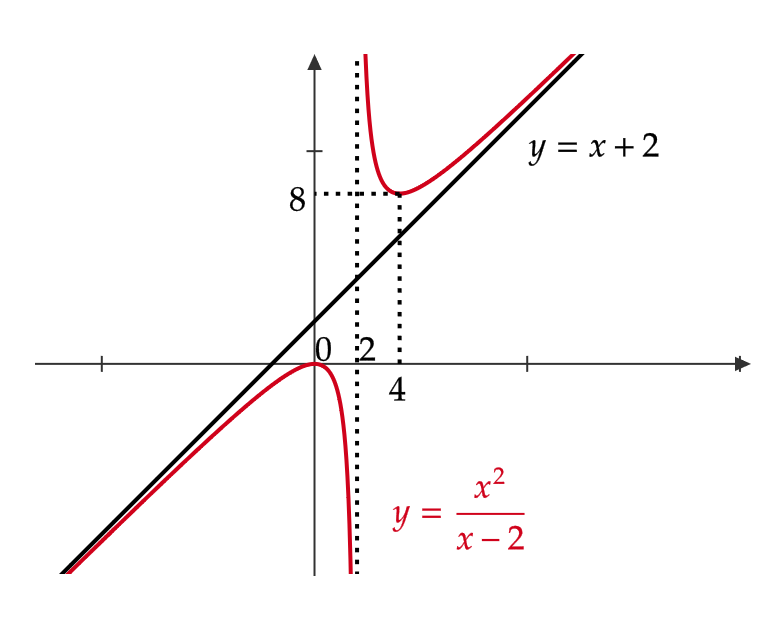
(2) \( y=\frac{x^2}{x-2} \) のグラフの概形を書く。
\( y \) は \( x=2 \) で定義されないことに注意。
$$ y=\frac{(x-2)(x+2)+4}{x-2}=x+2+\frac{4}{x-2} \tag{1} $$
と変形できる。
よって、
$$ y’=1-\frac{4}{(x-2)^2}=\frac{x(x-4)}{(x-2)^2} $$
$$ y^{\prime\prime}=-4\cdot \frac{-2}{(x-2)^3}=\frac{8}{(x-2)^3} $$
\( y’=0 \) となる \( x \) は \( x=0,4 \)
\( y^{\prime\prime}=0 \) となる \( x \) はない
よって、増減表をつくると、
| \( x \) | \( \cdots \) | \( 0 \) | \( \cdots \) | \( 2 \) | \( \cdots \) | \( 4 \) | \( \cdots \) |
| \( y’ \) | \( + \) | \( 0 \) | \( – \) | \( \times \) | \( – \) | \( 0 \) | \( + \) |
| \( y^{\prime\prime} \) | \( – \) | \( – \) | \( – \) | \( \times\) | \( + \) | \( + \) | \( + \) |
| \( y \) | ↱ | \( 0 \) | ⤵ | \( \times \) | ↳ | \( 8 \) | ⤴ |
よって、 \( y \) は \( x=0 \) で極大で、極大値 \( 0 \)
\( y \) は \( x=4 \) で極小で、極小値 \( 8 \)
変曲点はない
さらに、 \( \displaystyle \lim_{x\to \infty}\frac{4}{x-2}=0, \ \lim_{x\to-\infty}\frac{4}{x-2}=0 \) なので、式(1)より、
$$ \lim_{x\to\infty}(y-(x+2))=0, \ \lim_{x\to-\infty}(y-(x+2))=0 $$
よって、 \( x\to\infty, \ x\to-\infty \) のとき、この曲線は \( y=x+2 \) に近づく。
また、 \( \displaystyle \lim_{x\to 2+0}\frac{x^2}{x-2}=\infty, \ \lim_{x\to 2-0}\frac{x^2}{x-2}=-\infty \) である。
よって、グラフは次のように書くことができる。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

