こんにちは、ひかりです。
今回は高校数学から接線の方程式と関数の増減について解説していきます。
この記事では以下のことを紹介します。
- 接線の方程式の求め方について
- 法線の方程式の求め方について
- 関数の増減について
接線の方程式の求め方
曲線 \( y=f(x) \) 上の点 \( (a,f(a)) \) における接線の傾きは \( f'(a) \) でした。
よって、接線の方程式はある切片 \( b \) を用いて、 \( y=f'(a)x+b \) と書けます。
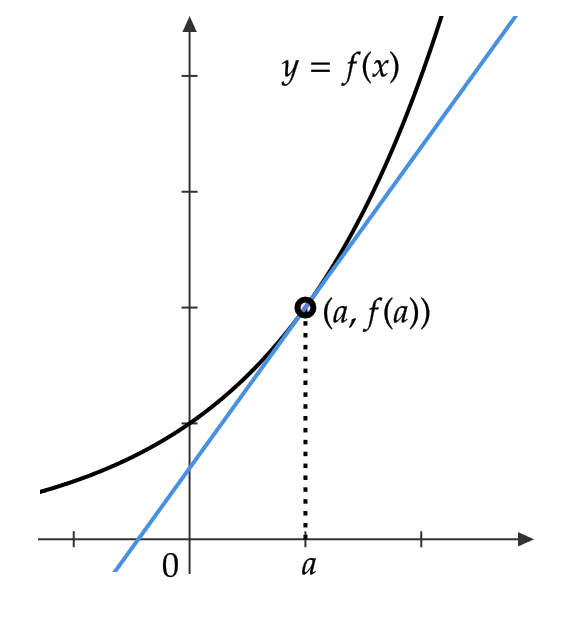
\( (a,f(a)) \) を代入すると、 \( f(a)=f'(a)a+b \) より、 \( b=f(a)-f'(a)a \)
したがって、
$$ y=f'(a)x+f(a)-f'(a)a $$
まとめると、次が成り立ちます。
曲線 \( y=f(x) \) 上の点 \( (a,f(a)) \) における接線の方程式は
$$ y-f(a)=f'(a)(x-a) $$
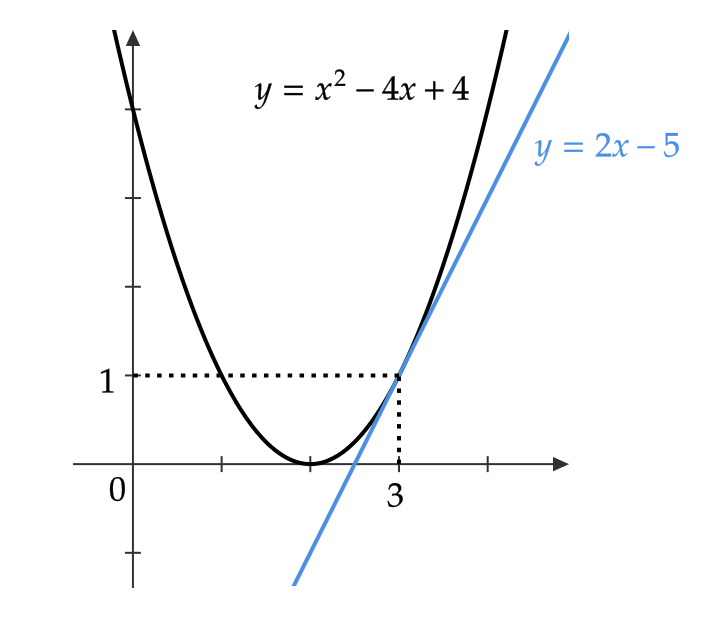
(1) \( y=x^2-4x+4 \) の点 \( (3,1) \) を通る接線の方程式を求める。
\( y’=2x-4 \) より、 \( x=3 \) のとき \( y’=2 \) である。
よって、接線の方程式は
$$ y-1=2(x-3) $$
なので \( y=2x-5 \)
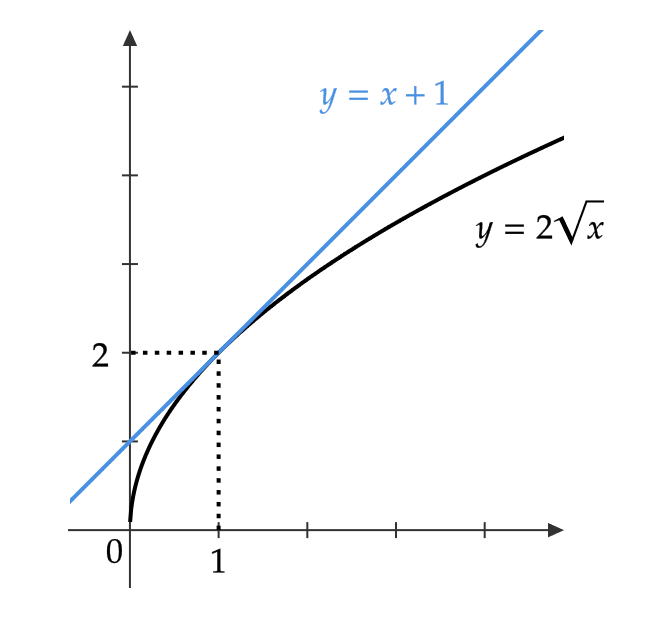
(2) \( y=2\sqrt{x} \) の点 \( (1,2) \) を通る接線の方程式を求める。
\( y’=\frac{1}{\sqrt{x}} \) より、 \( x=1 \) のとき \( y’=1 \) である。
よって、接線の方程式は
$$ y-2=1\cdot (x-1) $$
なので \( y=x+1 \)
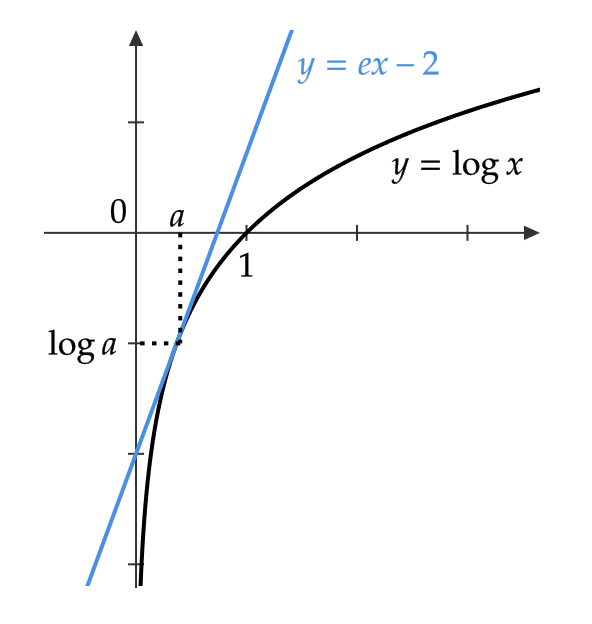
\( y=\log x \) について、次の接線の方程式を求める。
(1) 傾きが \( e \) の接線
\( y’=\frac{1}{x} \) より、点 \( (a,\log a) \) の接線の方程式は
$$ y-\log a=\frac{1}{a}(x-a) \tag{1} $$
ここで、傾きが \( e \) なので、 \( \frac{1}{a}=e \)
よって、 \( a=\frac{1}{e} \) なので、式(1)に代入すると、
$$ y-\log \frac{1}{e}=e(x-\frac{1}{e}) $$
なので、 \( y=ex-2 \)
(2) 原点から引いた接線
式(1)が原点 \( (0,0) \) を通るので、
$$ 0-\log a=\frac{1}{a}(0-a) $$
よって、 \( \log a=1 \) なので、 \( a=e \)
したがって、式(1)に \( a=e \) を代入すると、
$$ y-\log e=\frac{1}{e}(x-e) $$
なので、 \( y=\frac{1}{e}x \)
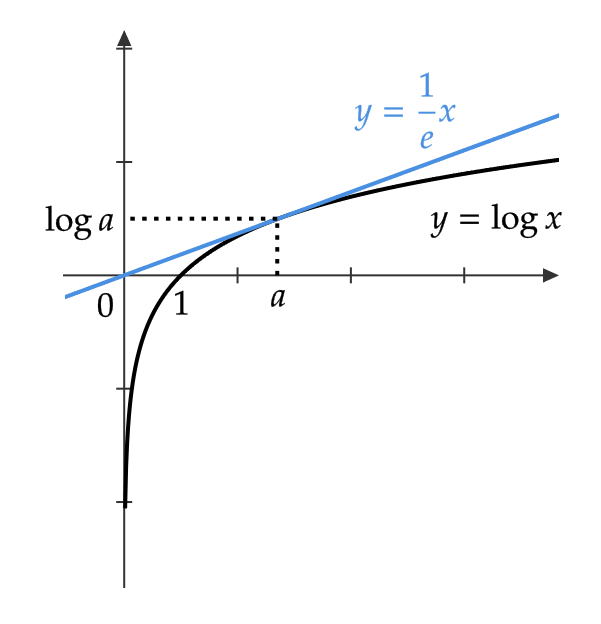
法線の方程式の求め方
曲線 \( y=f(x) \) 上の1点 \( P \) において、 \( P \) における接線と垂直に交わる直線を点 \( P \) におけるこの曲線の法線といいます。
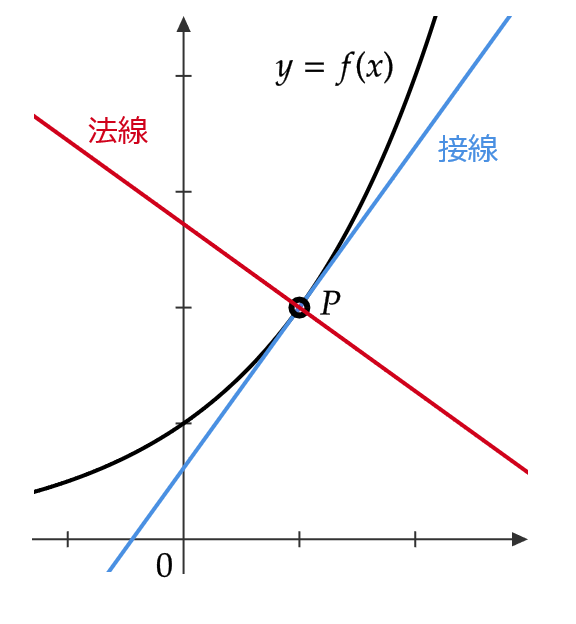
曲線 \( y=f(x) \) 上の点 \( (a,f(a)) \) における接線の傾きは \( f'(a) \) であるので、 \( f'(a)\not=0 \) のとき法線の傾きは \( -\frac{1}{f'(a)} \) となります。
(垂直な2つの直線の傾きを \( \alpha,\alpha’ \) とすると、 \( \alpha \cdot \alpha’=-1 \) となります。)
よって、法線の方程式はある切片 \( b \) を用いて、 \( y=-\frac{1}{f'(a)}x+b \) と書けます。
\( (a,f(a)) \) を代入すると、 \( f(a)=-\frac{1}{f'(a)}a+b \) より、 \( b=f(a)+\frac{1}{f'(a)}a \)
したがって、
$$ y=-\frac{1}{f'(a)}x+f(a)+\frac{1}{f'(a)}a $$
まとめると、次が成り立ちます。
曲線 \( y=f(x) \) 上の点 \( (a,f(a)) \) における法線の方程式は
$$ y-f(a)=-\frac{1}{f'(a)}(x-a) \quad (f'(a)\not=0) $$
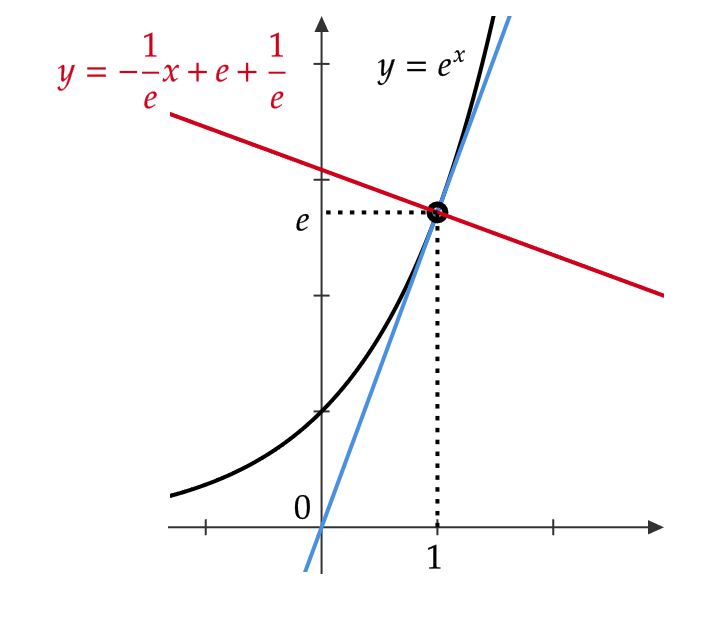
曲線 \( y=e^x \) の点 \( (1,e) \) における法線の方程式を求める。
\( y’=e^x \) より、点 \( (1,e) \) の法線の傾きは \( -\frac{1}{e} \)
よって、法線の方程式は
$$ y-e=-\frac{1}{e}(x-1) $$
なので、 \( y=-\frac{1}{e}x+e+\frac{1}{e} \)
関数の増減
曲線 \( y=f(x) \) 上の点 \( (a,f(a)) \) における接線の傾きは \( f'(a) \) でした。
このことから、次のことがわかります。
- \( f'(a)>0 \) ならば、接線は右上がりとなる。
- \( f'(a)<0 \) ならば、接線は右下がりとなる。
- \( f'(a)=0 \) ならば、接線は \( x \) 軸に平行となる。
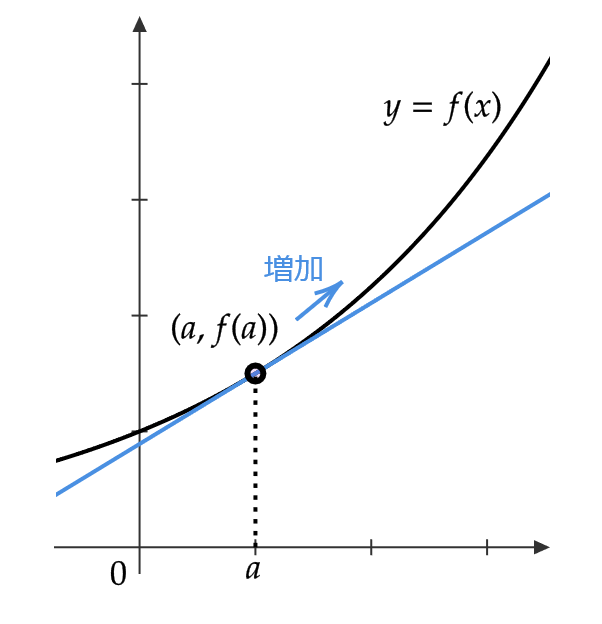
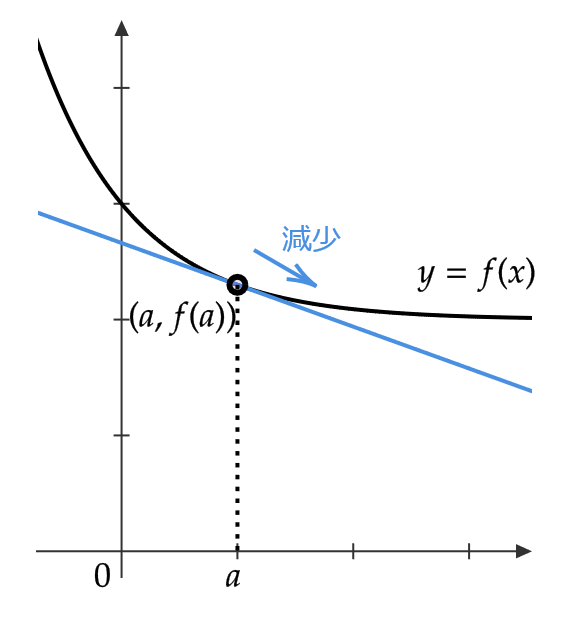
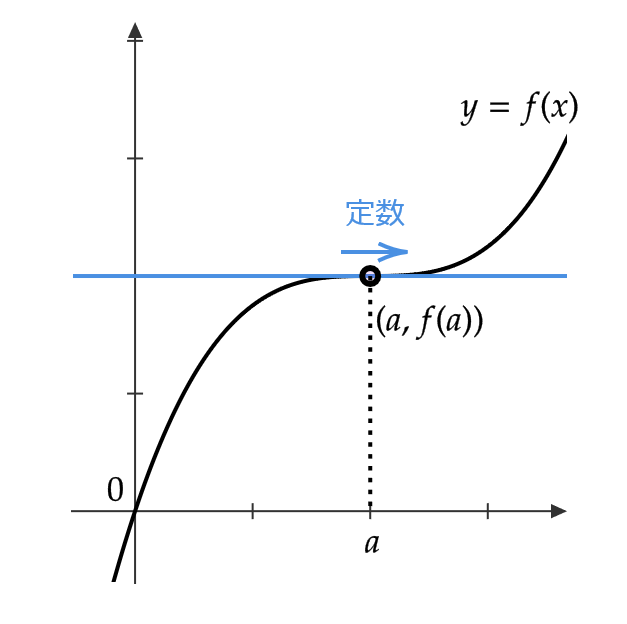
よって、
- \( f'(a)>0 \) ならば、 \( f(x) \) は \( x=a \) の近くで増加
- \( f'(a)<0 \) ならば、 \( f(x) \) は \( x=a \) の近くで減少
- \( f'(a)=0 \) ならば、 \( f(x) \) は \( x=a \) の近くで定数
したがって、次が成り立ちます。
(1) 区間 \( (a,b) \) でつねに \( f'(x)>0 \) ならば、 \( f(x) \) は区間 \( [a,b] \) で増加する。
(2) 区間 \( (a,b) \) でつねに \( f'(x)<0 \) ならば、 \( f(x) \) は区間 \( [a,b] \) で減少する。
(3) 区間 \( (a,b) \) でつねに \( f'(x)=0 \) ならば、 \( f(x) \) は区間 \( [a,b] \) で定数である。
(1) \( f(x)=\cos x \) のとき、 \( f'(x)=-\sin x \) であるので、区間 \( (0,\pi) \) で \( f'(x)<0 \) となる。
よって、区間 \( [0,\pi] \) で \( f(x) \) は減少する。
(2) \( f(x)=\log x \) のとき、 \( f'(x)=\frac{1}{x} \) であるので、区間 \( (0,\infty) \) で \( f'(x)>0 \) となる。
よって、区間 \( (0,\infty) \) で \( f(x) \) は増加する。
( \( x=0 \) では \( \log x \) は定義されないことに注意)
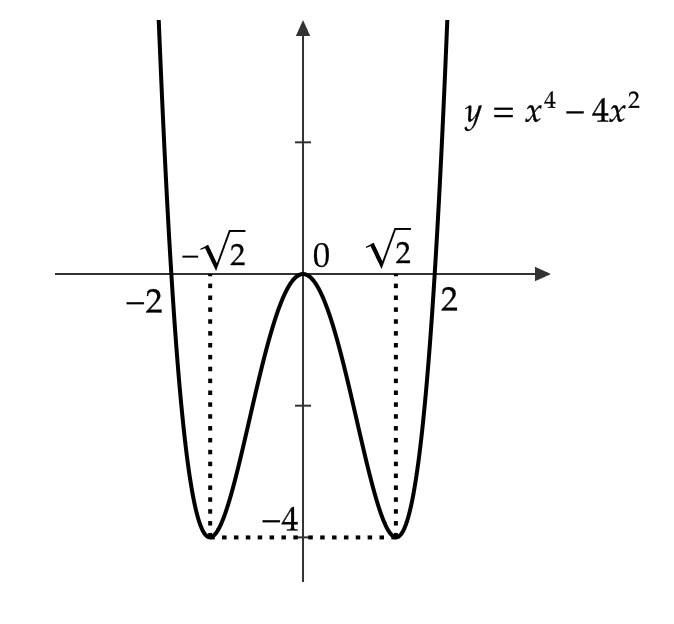
\( f(x)=x^4-4x^2 \) の増減を調べる。
\( f'(x)=4x^3-8x=4x(x^2-2) \) より、 \( f'(x)=0 \) となる \( x \) は \( x=0,\sqrt{2},-\sqrt{2} \)
\( x<-\sqrt{2} \) のとき、
$$ f'(x)=4x(x^2-2)<0 \quad (4x<0, \ x^2-2>0 \ \text{より}) $$
\( -\sqrt{2}<x<0 \) のとき、
$$ f'(x)=4x(x^2-2)>0 \quad (4x<0, \ x^2-2<0 \ \text{より}) $$
\( 0<x<\sqrt{2} \) のとき、
$$ f'(x)=4x(x^2-2)<0 \quad (4x>0, \ x^2-2<0 \ \text{より}) $$
\( \sqrt{2}<x \) のとき、
$$ f'(x)=4x(x^2-2)>0 \quad (4x>0, \ x^2-2>0 \ \text{より}) $$
よって、 \( f'(x) \) の符号および \( f(x) \) の増減は次の表のようになる。(これを増減表という)
| \( x \) | \( \cdots \) | \( -\sqrt{2} \) | \( \cdots \) | \( 0 \) | \( \cdots \) | \( \sqrt{2} \) | \( \cdots \) |
| \( f'(x) \) | \( – \) | \( 0 \) | \( + \) | \( 0 \) | \( – \) | \( 0 \) | \( + \) |
| \( f(x) \) | \( \color{red}{\searrow} \) | \( -4 \) | \( \color{red}{\nearrow} \) | \( 0 \) | \( \color{red}{\searrow} \) | \( -4 \) | \( \color{red}{\nearrow} \) |
(増加のときは \( \nearrow \) 、減少のときは \( \searrow \) とかく)
よって、 \( f(x) \) は区間
$$ -\sqrt{2}≦ x≦ 0, \ \sqrt{2}≦ x $$
で増加
区間
$$ x≦ -\sqrt{2}, \ 0≦ x≦ \sqrt{2} $$
で減少
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

