こんにちは、ひかりです。
今回は高校数学から三角関数について解説していきます。
この記事では以下のことを紹介します。
- 弧度法について
- 三角関数とその性質について
- 三角関数のグラフについて
- 三角関数の加法定理について
弧度法
いままでは、角の大きさを表すのに”度”を用いてきました。
これに対して、角の大きさを弧の長さで表す弧度法という表し方があります。
半径 \( 1 \) の円をとり、円周上に2点 \( A,B \) をとります。
このとき、弧 \( AB \) の長さが \( \theta \) のとき、 \( \angle AOB=\theta \) (ラジアン) と定めます。
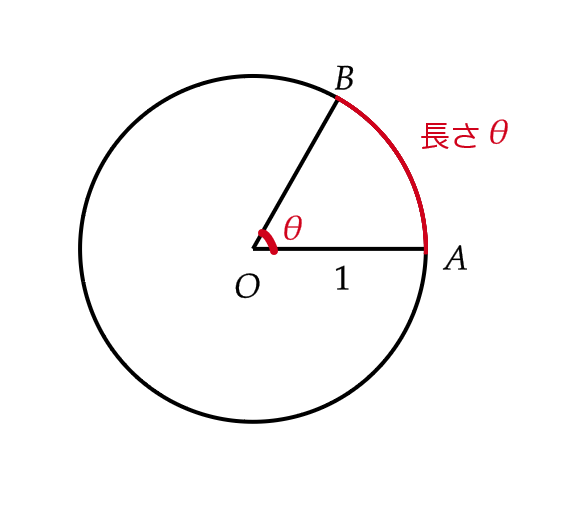
例えば、 \( \angle AOB=180^{\circ} \) とすると、弧 \( AB \) の長さは \( \frac{2\pi}{2}=\pi \) より、 \( 180^{\circ}=\pi \) (ラジアン) となります。
いろいろな角の度と弧度の関係をまとめる。
| 度 | \( 0^{\circ} \) | \( 30^{\circ} \) | \( 45^{\circ} \) | \( 60^{\circ} \) | \( 90^{\circ} \) | \( 180^{\circ} \) | \( 360^{\circ} \) |
| 弧度 | \( 0 \) | \( \frac{\pi}{6} \) | \( \frac{\pi}{4} \) | \( \frac{\pi}{3} \) | \( \frac{\pi}{2} \) | \( \pi \) | \( 2\pi \) |
三角関数とその性質
半径 \( r \) の円をかき、円周上の点 \( P \) の座標を \( (x,y) \) とします。
このとき、三角関数を次で定めます。
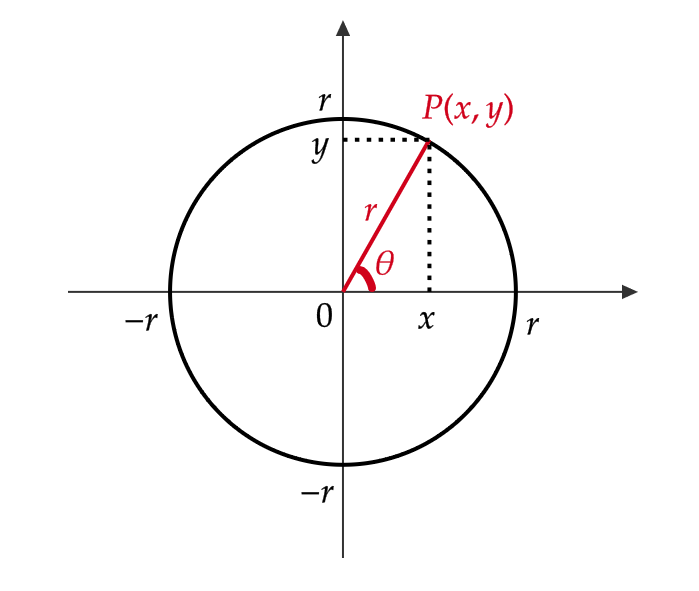
$$ \sin \theta=\frac{y}{r}, \ \cos \theta=\frac{x}{r}, \ \tan\theta=\frac{y}{x} $$
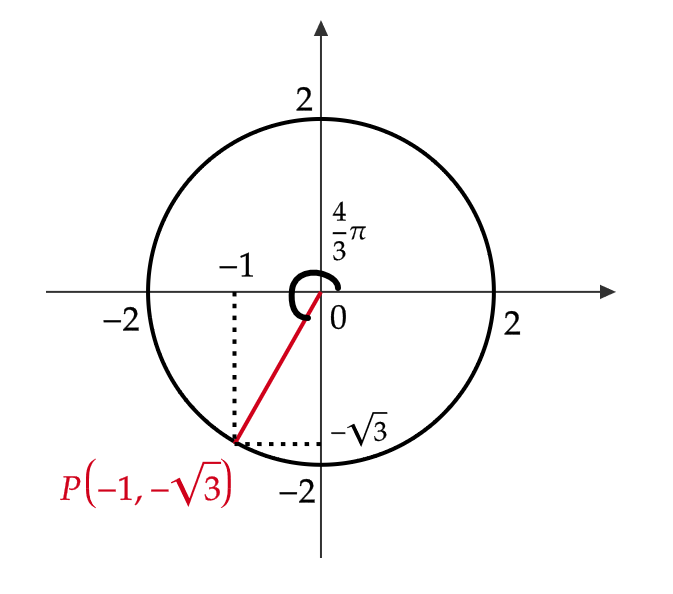
\( \theta=\frac{4}{3}\pi(=240^{\circ}) \) のとき、半径2の円をかくと、 \( P(-1,-\sqrt{3}) \) となるので、
$$ \sin\frac{4}{3}\pi=\frac{y}{r}=\frac{-\sqrt{3}}{2}=-\frac{\sqrt{3}}{2} $$
$$ \cos\frac{4}{3}\pi=\frac{x}{r}=\frac{-1}{2}=-\frac{1}{2} $$
$$ \tan\frac{4}{3}\pi=\frac{y}{x}=\frac{-\sqrt{3}}{-1}=\sqrt{3} $$
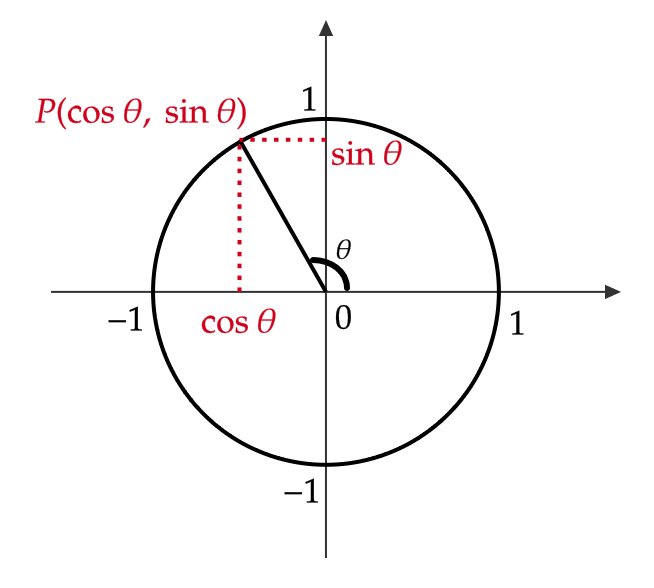
三角関数の定義より、半径 \( 1 \) の円(単位円)の円周上の点 \( P(x,y) \) は \( \sin\theta=y, \ \cos\theta=x \) より、 \( P(\cos\theta,\sin\theta) \) となります。
点 \( P \) は単位円周上の点なので、次が成り立ちます。
$$ -1≦ \sin\theta≦ 1, \ -1≦ \cos\theta≦ 1 $$
また、三角関数 \( \sin\theta,\cos\theta,\tan\theta \) の間に次の関係があります。
(1) \( \sin^2\theta+\cos^2\theta=1 \)
(2) \( \tan\theta=\frac{\sin\theta}{\cos\theta} \)
(3) \( 1+\tan^2\theta=\frac{1}{\cos^2\theta} \)
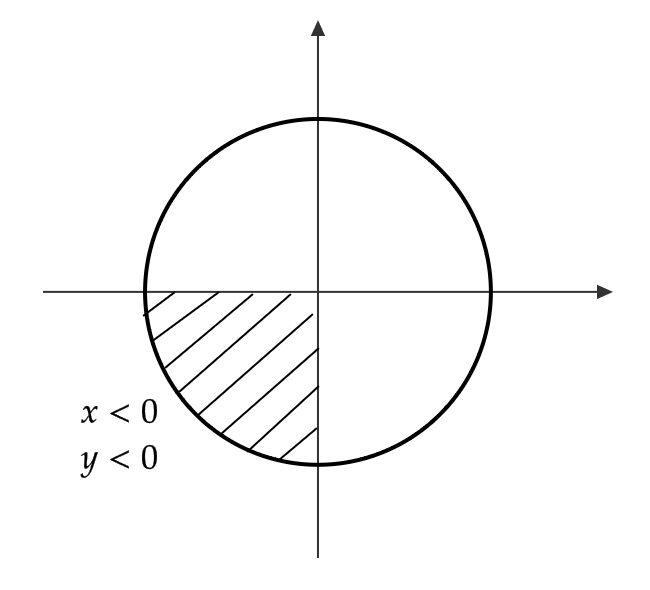
\( \theta \) が第3象限の角で \( \cos\theta=-\frac{3}{5} \) のとき、 \( \sin\theta,\tan\theta \) を求める。
\( \sin^2\theta+\cos^2\theta=1 \) より、
$$ \sin^2\theta=1-\cos^2\theta=1-\left(-\frac{3}{5}\right)^2=\frac{16}{25} $$
\( \theta \) が第3象限の角なので、 \( \sin\theta=\frac{y}{r}<0 \)
よって、 \( \sin\theta=-\sqrt{\frac{16}{25}}=-\frac{4}{5} \)
また、\( \tan\theta=\frac{\sin\theta}{\cos\theta}=\frac{-\frac{4}{5}}{-\frac{3}{5}}=\frac{4}{3} \)
三角関数のグラフ
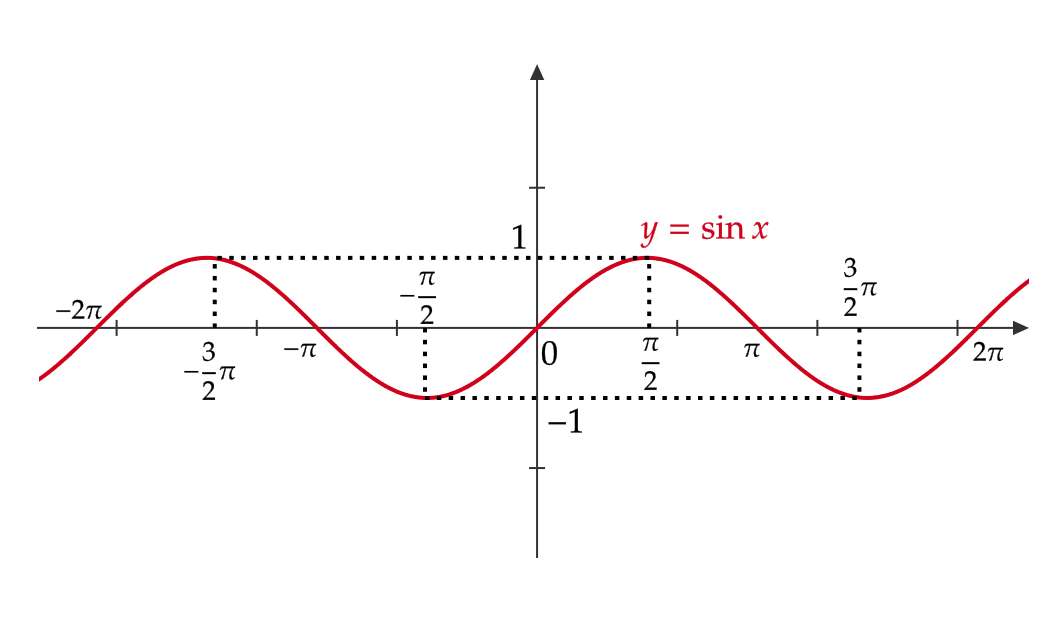
\( y=\sin x \) のグラフ
次のようなグラフとなります。
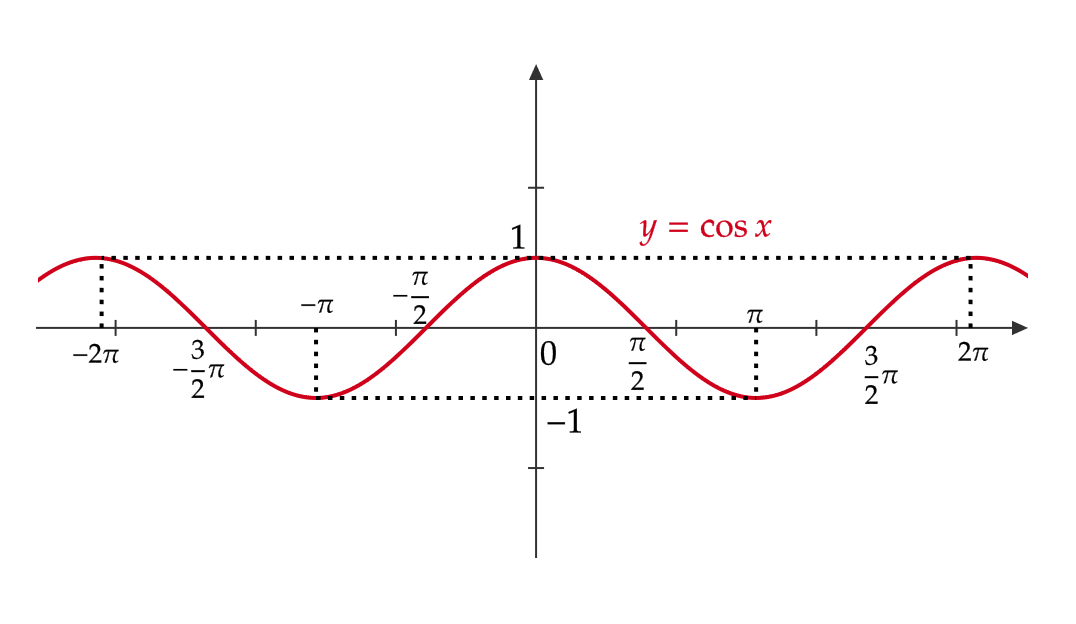
\( y=\cos x \) のグラフ
次のようなグラフとなります。
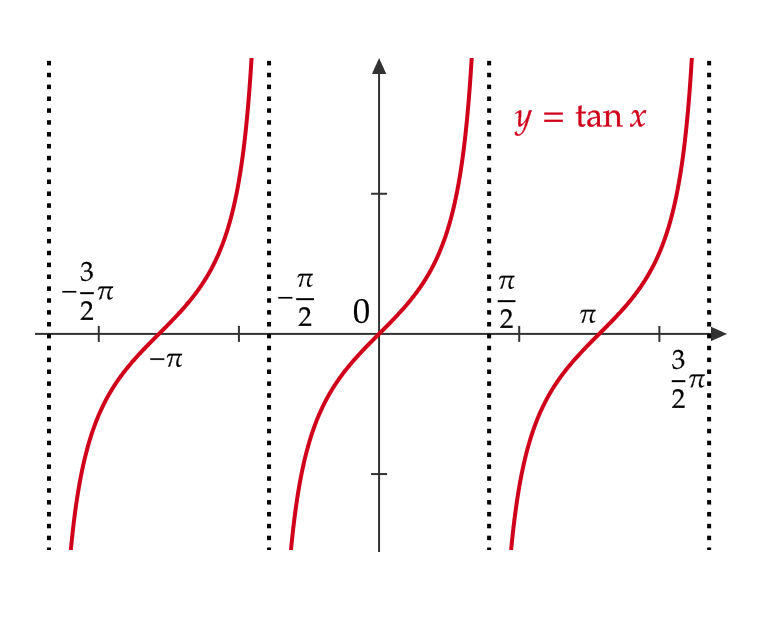
\( y=\tan x \) のグラフ
次のようなグラフとなります。
三角関数の加法定理
角の和や差の三角関数に対して、次の加法定理が成り立ちます。
(1) \( \sin\theta \) の加法定理
$$ \begin{align} \sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \sin(\alpha-\beta)&=\sin\alpha\cos\beta-\cos\alpha\sin\beta \end{align} $$
(2) \( \cos\theta \) の加法定理
$$ \begin{align} \cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta \\ \cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align} $$
(3) \( \tan\theta \) の加法定理
$$ \begin{align} \tan(\alpha+\beta)&=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \\ \tan(\alpha-\beta)&=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{align} $$
(1) \( \sin75^{\circ} \) を計算する。
$$ \begin{align} \sin75^{\circ}&=\sin(45^{\circ}+30^{\circ})=\sin45^{\circ}\cos30^{\circ}+\cos45^{\circ}\sin30^{\circ} \\ &=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4} \end{align} $$
(2) \( \cos15^{\circ} \) を計算する。
$$ \begin{align} \cos15^{\circ}&=\cos(45^{\circ}-30^{\circ})=\cos45^{\circ}\cos30^{\circ}+\sin45^{\circ}\sin30^{\circ} \\ &=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4} \end{align} $$
(3) \( \tan75^{\circ} \) を計算する。
$$ \begin{align} \tan75^{\circ}&=\tan(45^{\circ}+30^{\circ})=\frac{\tan45^{\circ}+\tan30^{\circ}}{1-\tan45^{\circ}\tan30^{\circ}} \\ &=\frac{1+\frac{1}{\sqrt{3}}}{1-1\cdot\frac{1}{\sqrt{3}}}=\frac{\frac{\sqrt{3}+1}{\sqrt{3}}}{\frac{\sqrt{3}-1}{\sqrt{3}}}=\frac{\sqrt{3}+1}{\sqrt{3}-1}=\frac{(\sqrt{3}+1)^2}{(\sqrt{3}-1)(\sqrt{3}+1)} \\ &=\frac{3+2\sqrt{3}+1}{3-1}=2+\sqrt{3} \end{align} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

