こんにちは、ひかりです。
今回は高校数学からさまざまな関数とそのグラフについて解説していきます。
この記事では以下のことを紹介します。
- 一次関数・二次関数・円とそのグラフについて
- 分数関数・無理関数とそのグラフについて
- 逆関数と合成関数について
一次関数・二次関数・円
2つの変数 \( x,y \) に対して、 \( x \) の値を定めるとそれに応じて \( y \) の値がただ一つ定まるとき、 \( y \) は \( x \) の関数であるといいます。
\( y \) が \( x \) の関数であるとき、 \( y=f(x) \) などと表します。
一次関数
\( a,b \) を定数として、 \( a\not=0 \) とします。
このとき、一次関数 \( y=ax+b \) のグラフは次のようになります。
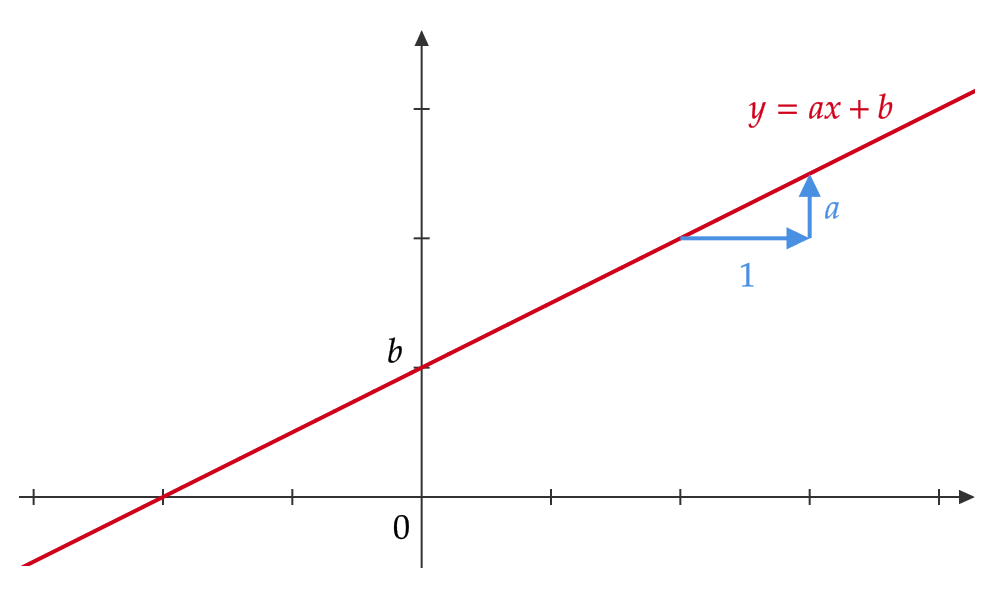
このとき、 \( a \) をこのグラフの傾きといい、 \( b \) を切片といいます。
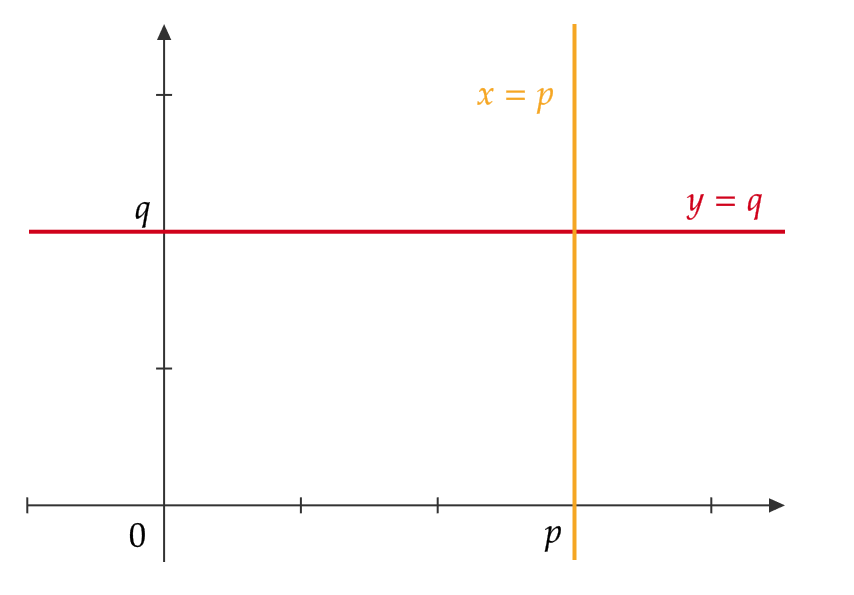
特に、 \( y \) 軸に平行な直線は \( x=p \) 、 \( x \) 軸に平行な直線は \( y=q \) と表せます。
二次関数
次に、二次関数 \( y=ax^2 \ (a\not=0) \) のグラフは次のようになります。
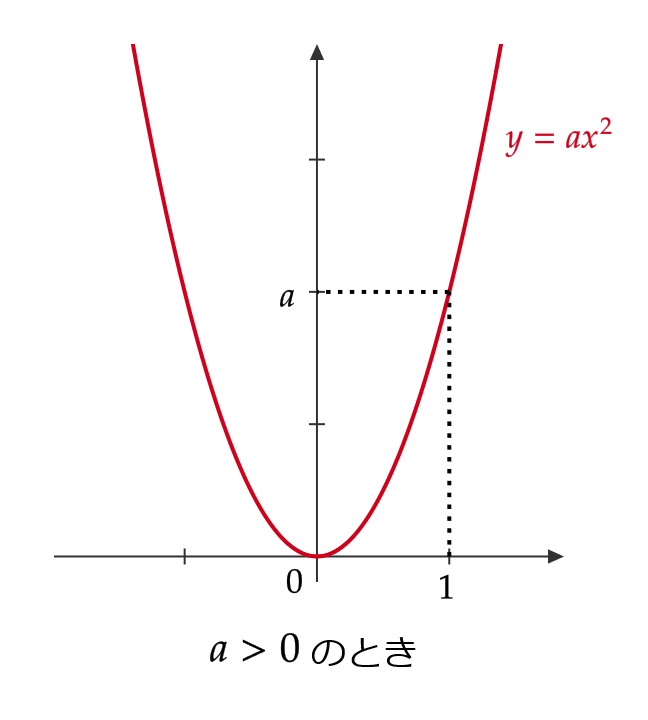
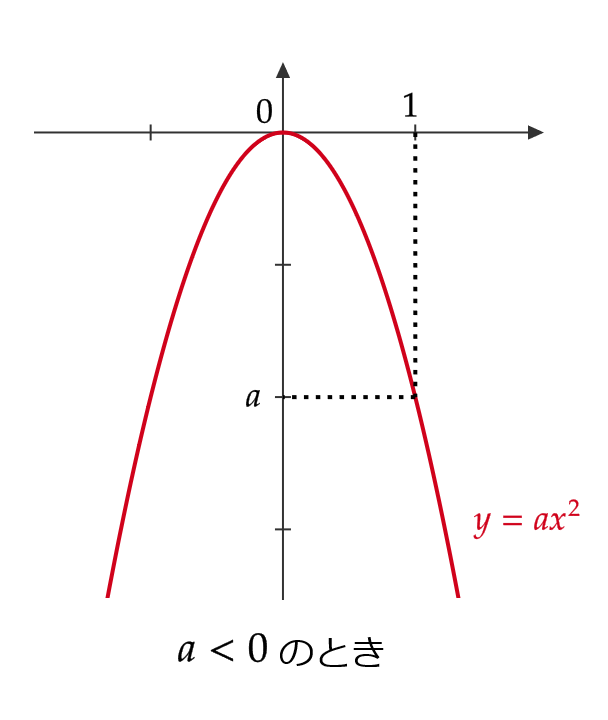
また、二次関数の平行移動について次が成り立ちます。
\( y=a(x-\color{blue}{p})^2+\color{green}{q} \) のグラフは、 \( y=ax^2 \) のグラフを \( x \) 軸の方向に \( \color{blue}{p} \) 、 \( y \) 軸の方向に \( \color{green}{q} \) だけ平行移動した関数となる。
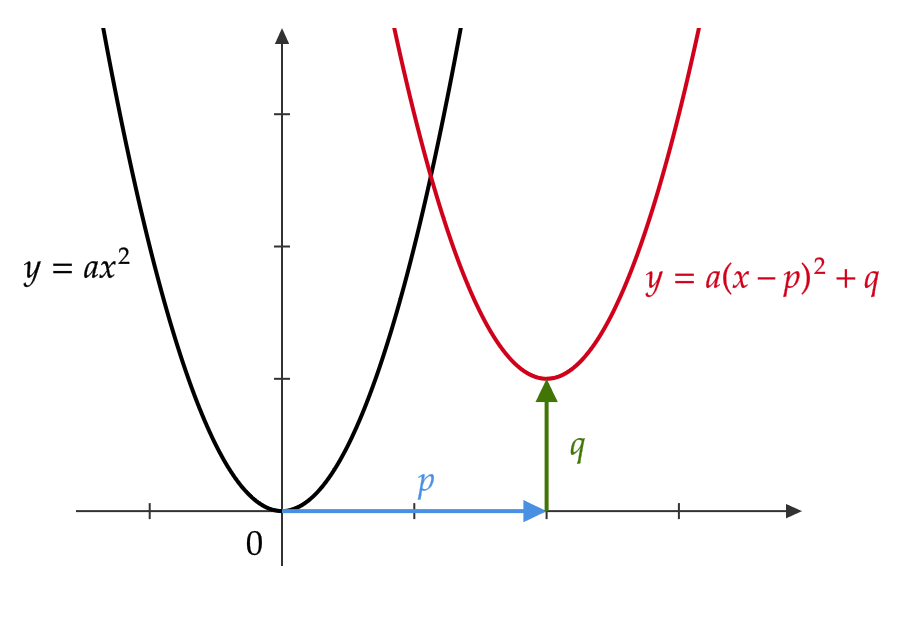
(1) \( y=2(x-3)^2+4 \) のグラフを考える。
これは、 \( y=2x^2 \) のグラフを \( x \) 軸の方向に \( 3 \) 、 \( y \) 軸の方向に \( 4 \) だけ平行移動した関数となる。
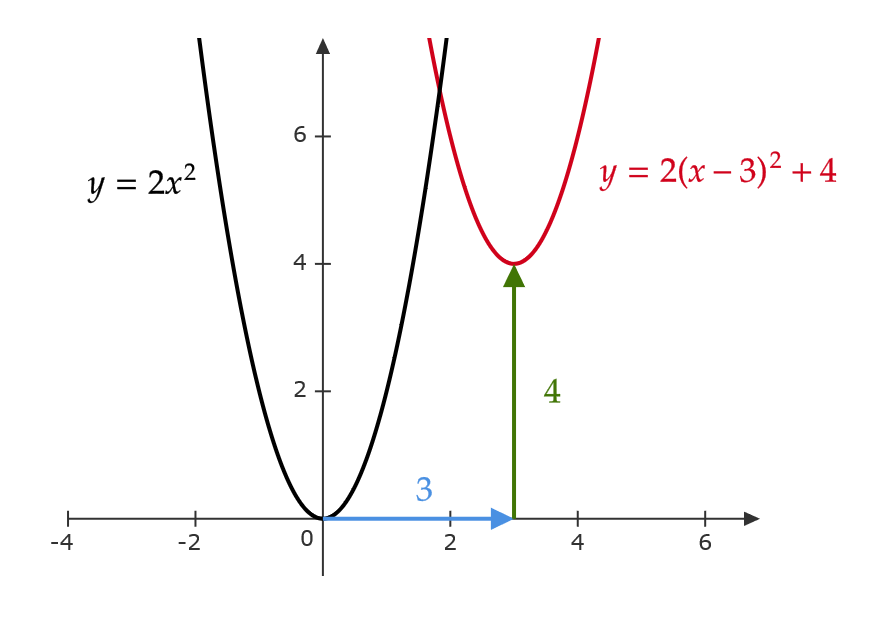
(2) \( y=x^2-x+1 \) のグラフを考える。
$$ \begin{align} y&=x^2-x+1=\left( x^2-x\color{red}{+\frac{1}{4}}\right)+1\color{red}{-\frac{1}{4}} \\ &=\left( x-\frac{1}{2}\right)^2+\frac{3}{4} \end{align} $$
なので、 \( y=x^2 \) のグラフを \( x \) 軸の方向に \( \frac{1}{2} \) 、 \( y \) 軸の方向に \( \frac{3}{4} \) だけ平行移動した関数となる。
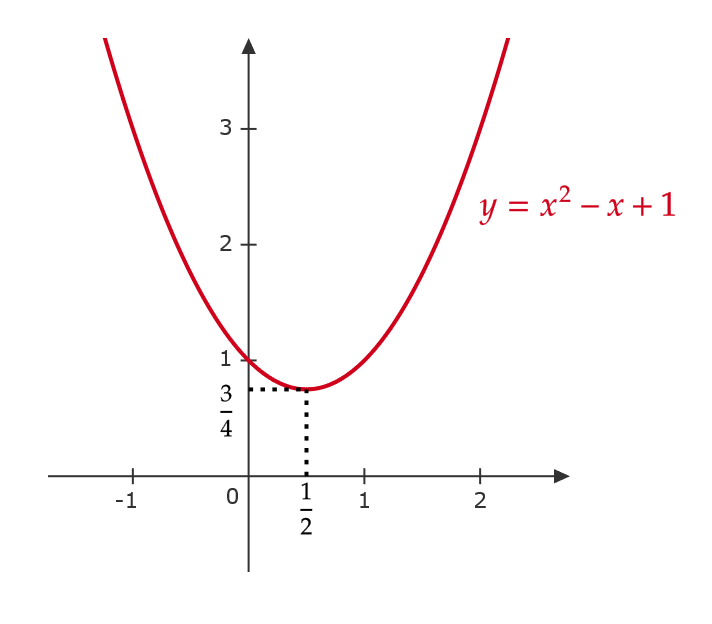
例1(2)のように、 \( ax^2+bx+c \) を \( a(x-p)^2+q \) の形に変形することを平方完成といいます。
円の方程式
点 \( C(a,b) \) を中心とする半径 \( r \) の円を考えます。
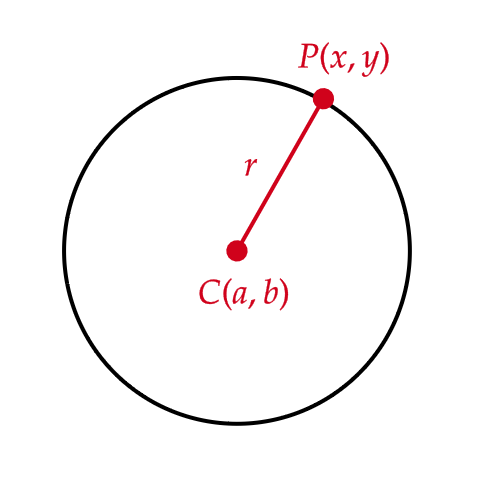
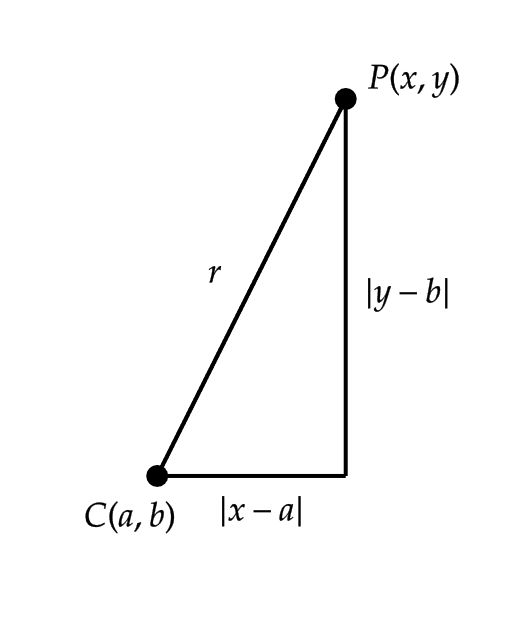
このとき、この円周上の点を \( P(x,y) \) とすると、 \( CP \) の長さは次のようになります。
$$ CP=\sqrt{(x-a)^2+(y-b)^2} $$
一方で、 \( CP=r \) より、次が成り立ちます。
$$ \sqrt{(x-a)^2+(y-b)^2}=r $$
よって、両辺2乗すると、 \( (x-a)^2+(y-b)^2=r^2 \) となります。
これが中心 \( C(a,b) \) 、半径 \( r \) の円の方程式となります。まとめると、
点 \( (a,b) \) を中心とする半径 \( r \) の円の方程式は
$$ (x-a)^2+(y-b)^2=r^2 $$
とくに、原点を中心とする半径 \( r \) の円の方程式は
$$ x^2+y^2=r^2 $$
(1) 原点を中心とする半径 \( 1 \) の円(これを単位円という)の方程式は
$$ x^2+y^2=1 $$
(2) 点 \( (2,-1) \) を中心とする半径 \( \sqrt{3} \) の円の方程式は
$$ (x-2)^2+(y+1)^2=3 $$
分数関数・無理関数
分数関数
\( y=\frac{1}{x} \) や \( y=\frac{x^2-1}{x+2} \) のように分数式で表される関数を分数関数といいます。
\( y=\frac{k}{x} \ (k\not=0) \) のグラフ
これは反比例のグラフとなります。
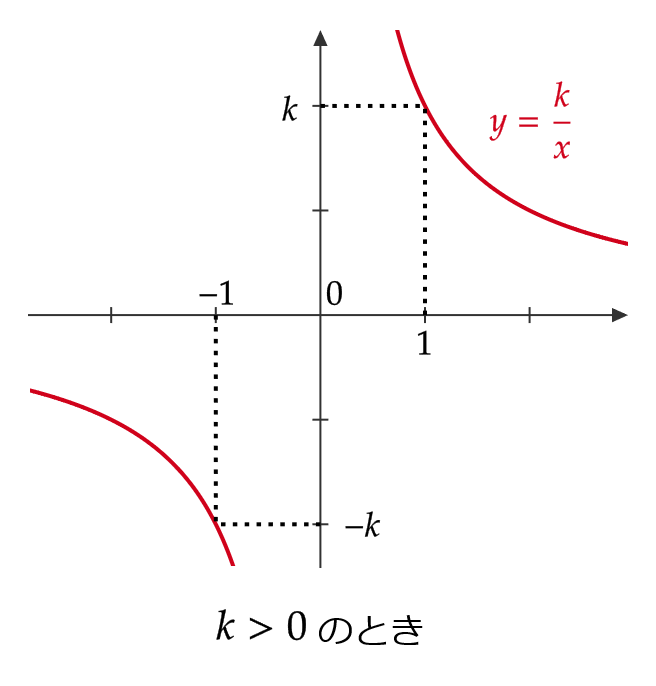
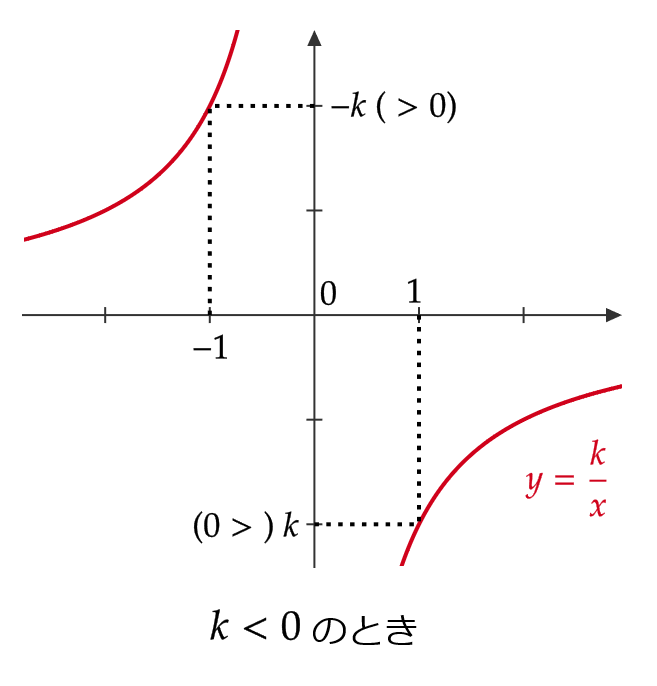
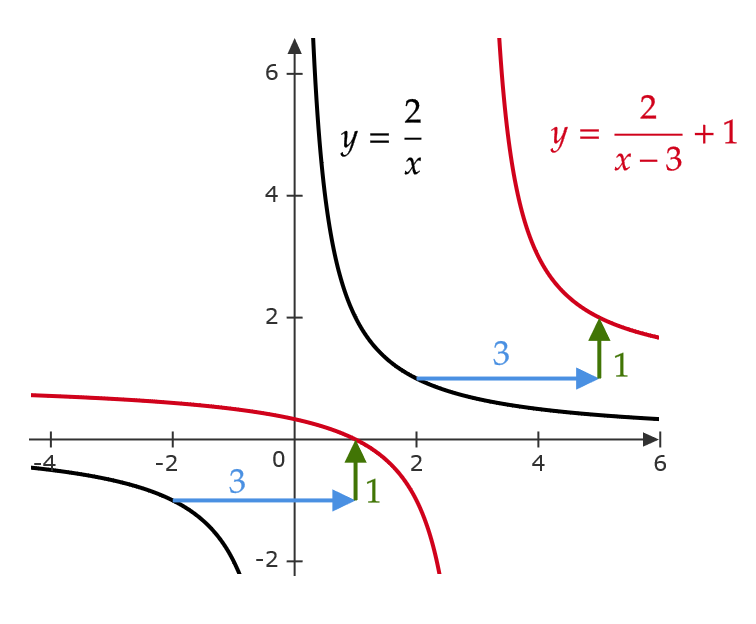
\( y=\frac{k}{x-p}+q \ (k\not=0) \) のグラフ
これは \( y=\frac{k}{x} \) のグラフを平行移動して得られます。
\( y=\frac{k}{x-\color{blue}{p}}+\color{green}{q} \) のグラフは、 \( y=\frac{k}{x} \) のグラフを \( x \) 軸の方向に \( \color{blue}{p} \) 、 \( y \) 軸の方向に \( \color{green}{q} \) だけ平行移動した関数となる。
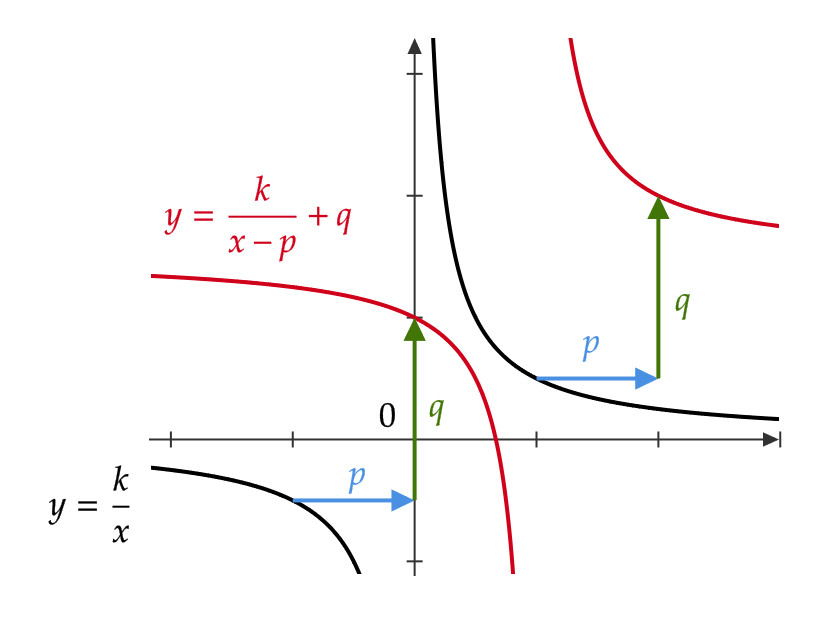
\( y=\frac{2}{x-3}+1 \) のグラフを考える。
これは、 \( y=\frac{2}{x} \) のグラフを \( x \) 軸の方向に \( 3 \) 、 \( y \) 軸の方向に \( 1 \) だけ平行移動した関数となる。
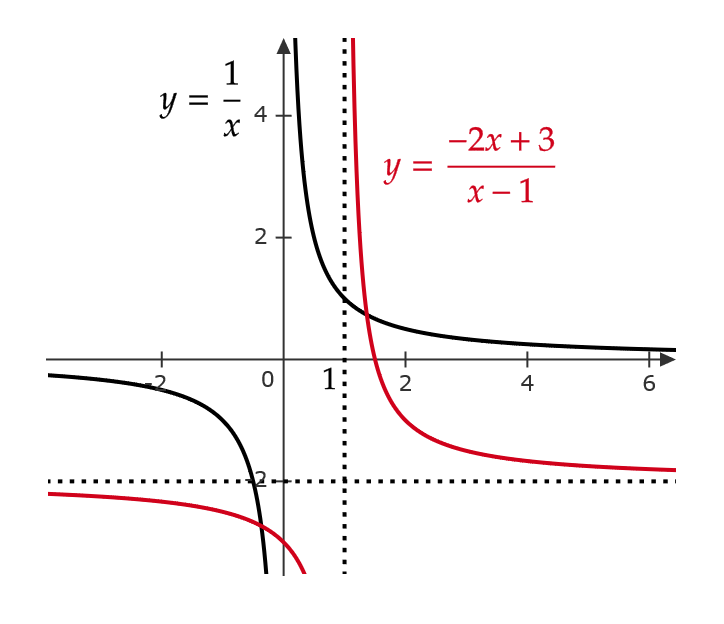
\( y=\frac{ax+b}{cx+d} \) のグラフ
これは \( y=\frac{k}{x-p}+q \) の形に変形することができます。
\( y=\frac{-2x+3}{x-1} \) のグラフを考える。
$$ y=\frac{-2x+3}{x-1}=\frac{-2(x-1)+1}{x-1}=\frac{1}{x-1}-2 $$
と変形できるので、これは、\( y=\frac{1}{x} \) のグラフを \( x \) 軸の方向に \( 1 \) 、 \( y \) 軸の方向に \( -2 \) だけ平行移動した関数となる。
無理関数
\( \sqrt{x}, \ \sqrt{4-2x}, \ \sqrt{x^2+1} \) のようにルートの中に文字を含む関数を無理関数といいます。
\( y=\sqrt{ax} \ (a\not=0) \) のグラフ
\( a \) の正負によって次のようになります。
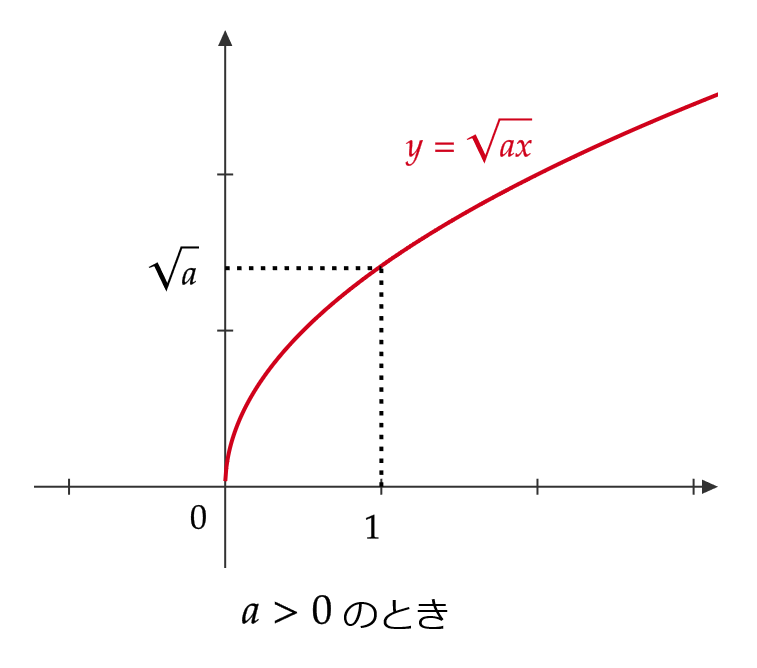
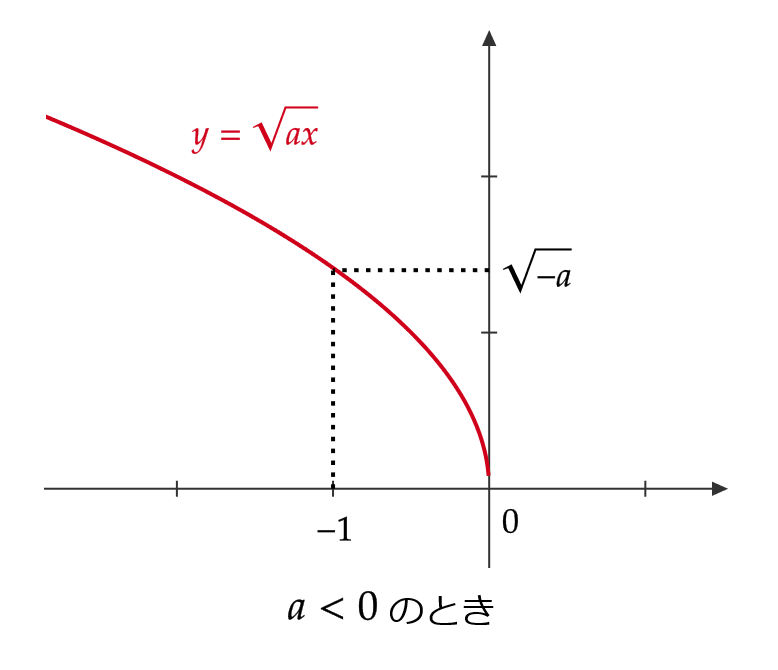
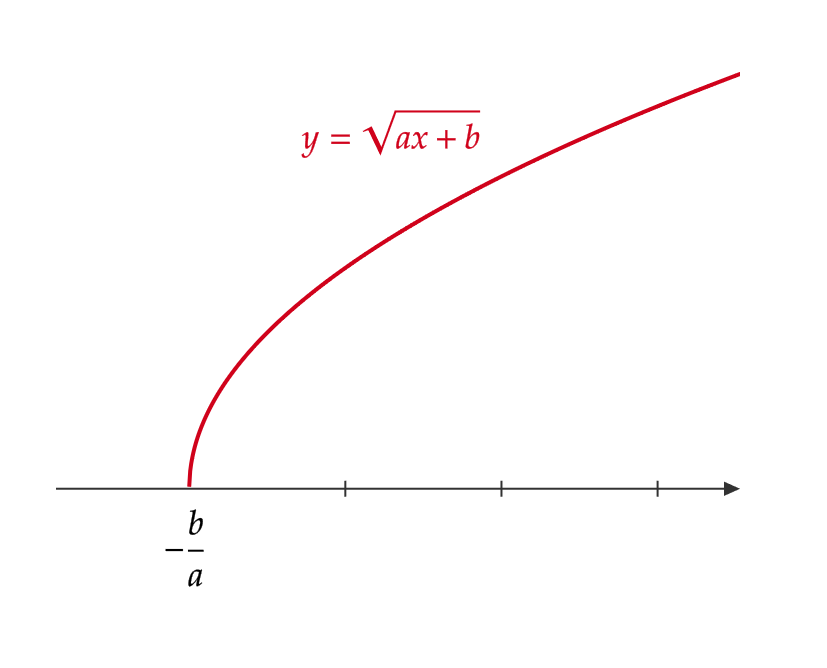
\( y=\sqrt{ax+b} \ (a\not=0) \) のグラフ
これは \( y=\sqrt{ax} \) のグラフを平行移動して得られます。
\( y=\sqrt{ax+b} \) のグラフは、 \( y=\sqrt{ax} \) のグラフを \( x \) 軸の方向に \( -\frac{b}{a} \) だけ平行移動した関数となる。
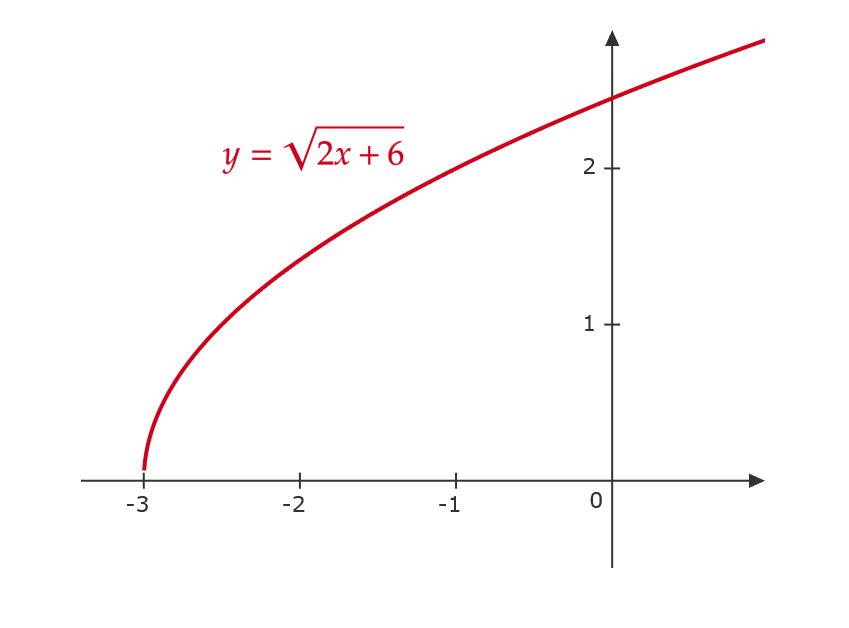
\( y=\sqrt{2x+6} \) のグラフを考える。
これは、\( y=\sqrt{2x} \) のグラフを \( x \) 軸の方向に \( -3 \) だけ平行移動した関数となる。
逆関数と合成関数
逆関数
関数 \( y=f(x) \) を \( x \) について解いて、ただ一つの解 \( x=g(y) \) が得られたとします。
このとき、 \( x \) と \( y \) を入れ替えた関数 \( y=g(x) \) を \( y=f(x) \) の逆関数といい、 \( y=f^{-1}(x) \) で表します。
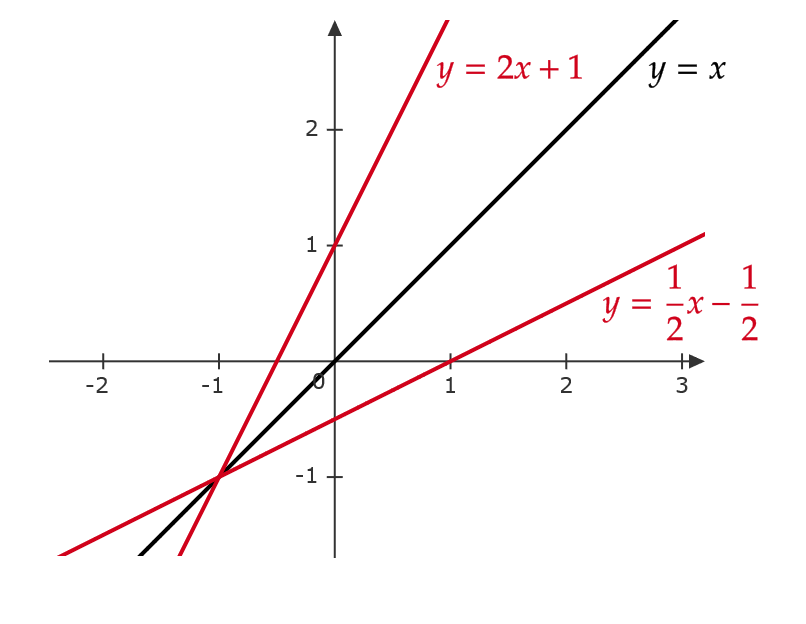
(1) 関数 \( y=2x+1 \) の逆関数を求める。
\( x \) について解くと、 \( x=\frac{1}{2}y-\frac{1}{2} \)
よって、逆関数は \( x \) と \( y \) を入れ替えて \( y=\frac{1}{2}x-\frac{1}{2} \)
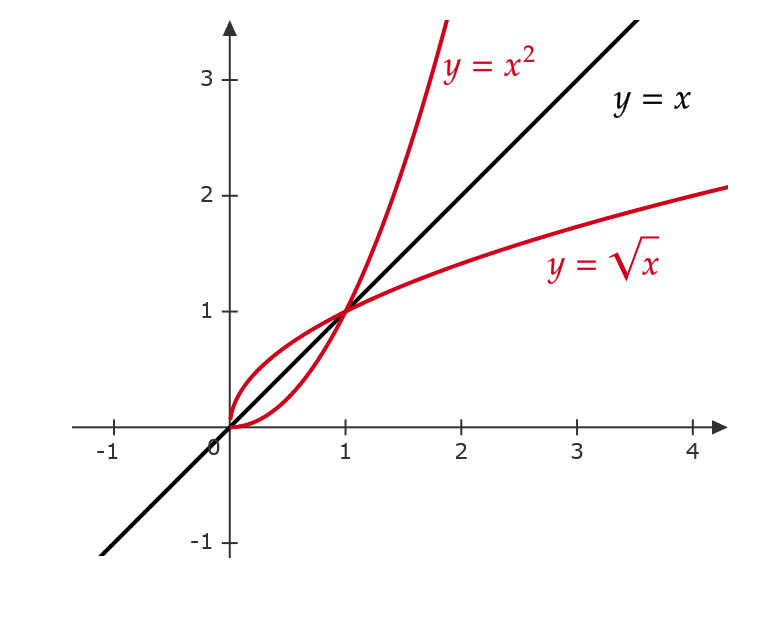
(2) 関数 \( y=x^2 \) の逆関数は考えられない。
しかし、定義域を制限した \( y=x^2 \ ( x≧ 0) \) については逆関数を考えられる。
\( x \) について解くと、 \( x=\sqrt{y} \ (y≧ 0) \)
よって、逆関数は \( x \) と \( y \) を入れ替えて \( y=\sqrt{x} \ (x≧0) \)
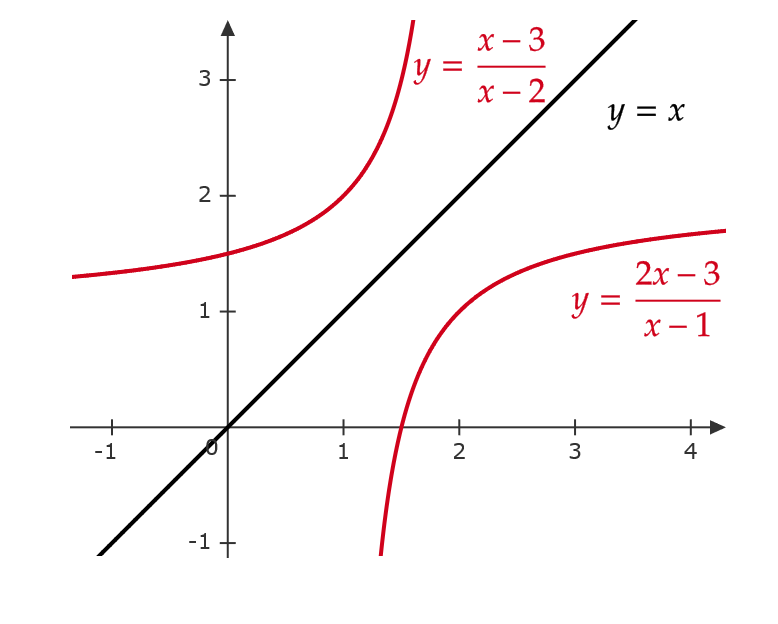
関数 \( y=\frac{2x-3}{x-1} \ (x>1) \) の逆関数を求める。
この関数の定義域は \( x>1 \) 、値域は \( y<2 \) となる。(値域は後に紹介する「極限」を用いるとわかる)
\( (x-1)y=2x-3 \) より、 \( x \) について解くと、 \( x=\frac{y-3}{y-2} \ (x<2) \)
よって、逆関数は \( y=\frac{x-3}{x-2} \ (x<2) \)
この関数の定義域は \( x<2 \) 、値域は \( y>1 \) となる。
また、グラフを見ると \( y=x \) に対して対称になっている。
合成関数
2つの関数 \( y=f(x) \) と \( z=g(y) \) があるとき、 \( g(y) \) に \( y=f(x) \) を代入すると、 \( z=g(f(x)) \) が得られます。
この関数を \( f \) と \( g \) の合成関数といい、 \( g\circ f(x)=g(f(x)) \) と表します。(順番に注意してください)
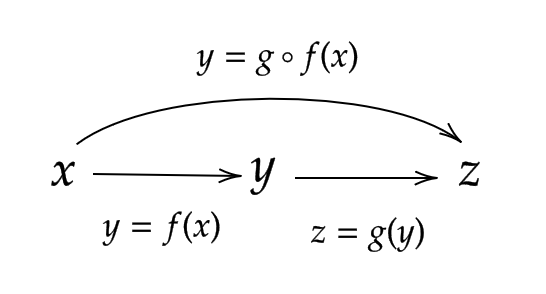
\( f(x)=x^2, \ g(x)=2x+1 \) のとき、
$$ g\circ f(x)=g(f(x))=g(x^2)=2x^2+1 $$
$$ f\circ g(x)=f(g(x))=f(2x+1)=(2x+1)^2=4x^2+4x+1 $$
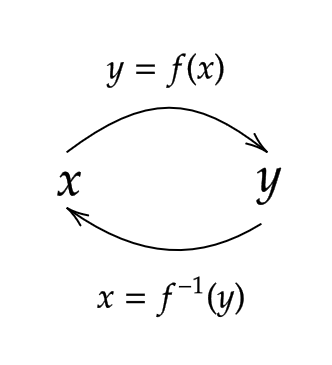
逆関数との合成関数
関数 \( y=f(x) \) が逆関数 \( f^{-1}(x) \) をもつとき、
$$ (f^{-1}\circ f)(x)=f^{-1}(f(x))=x $$
$$ (f\circ f^{-1})(y)=f(f^{-1}(y))=y $$
が成り立ちます。
\( f(x)=2x+1 \) の逆関数は \( f^{-1}(x)=\frac{1}{2}x-\frac{1}{2} \) であった。このとき、
$$ (f^{-1}\circ f)(x)=f^{-1}(f(x))=f^{-1}(2x+1)=\frac{1}{2}(2x+1)-\frac{1}{2}=x $$
$$ (f\circ f^{-1})(y)=f(f^{-1}(y))=f\left(\frac{1}{2}y-\frac{1}{2}\right)=2\left(\frac{1}{2}y-\frac{1}{2}\right)+1=y $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

