曲線・曲面論10：さまざまな曲面の曲率の計算

\( x=f(u), y=0, z=g(u) \) で表される曲線を \( z \) 軸の周りに回転して得られる回転面を \( S \) とする。ただし、

\[ f(u)>0, \ (f'(u))^2+(g'(u))^2\not=0, \quad {}’=\frac{d}{du} \]

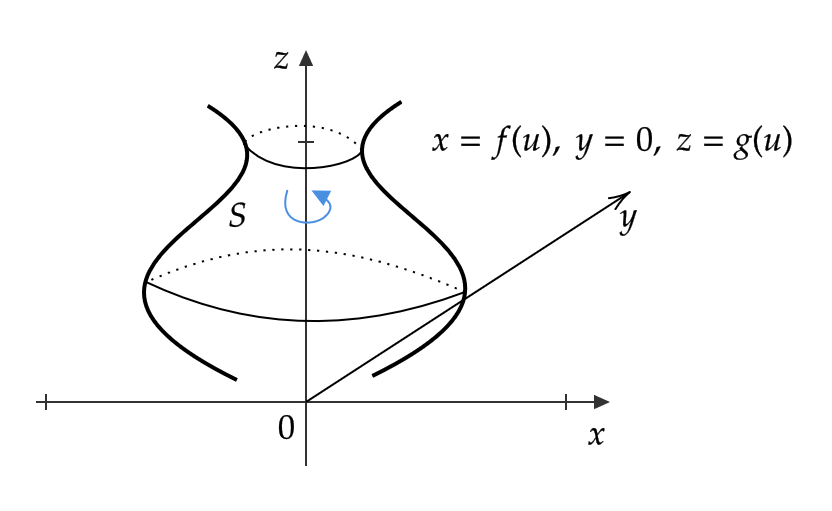
\[ S=\{\mathbf{p}(u,v)=(f(u)\cos v,f(u)\sin v,g(u)) : 0≦v<2\pi \} \]

として、 \( \varphi=(f’)^2+(g’)^2 \) とおく。

\[ \mathbf{p}_u=(f’\cos v,f’\sin v,g’), \quad \mathbf{p}_v=(-f\sin v,f\cos v,0) \]

であるので、

\[ E=\mathbf{p}_u\cdot\mathbf{p}_u=\varphi, \quad F=\mathbf{p}_u\cdot \mathbf{p}_v=0, \quad G=\mathbf{p}_v\cdot\mathbf{p}_v=f^2 \]

次に、 \( \mathbf{n}=\frac{\mathbf{p}_u\times \mathbf{p}_v}{\|\mathbf{p}_u\times \mathbf{p}_v\|} \) を求める。

\[ \mathbf{p}_u\times\mathbf{p}_v=\det\begin{pmatrix} \mathbf{e}_x & \mathbf{e}_y & \mathbf{e}_z \\ f’\cos v & f’\sin v & g’ \\ -f\sin v & f\cos v & 0 \end{pmatrix}=(-fg’\cos v,-fg’\sin v,ff’) \]

より、 \( \|\mathbf{p}_u\times\mathbf{p}_v\|=f\sqrt{\varphi} \) であるので、

\[ \mathbf{n}=\frac{1}{\sqrt{\varphi}}(-g’\cos v,-g’\sin v,f’) \]

したがって、

\[ \mathbf{p}_{uu}=(f^{\prime\prime}\cos v,f^{\prime\prime}\sin v,g^{\prime\prime}), \quad \mathbf{p}_{uv}=(-f’\sin v,f’\cos v,0) \]

\[ \mathbf{p}_{vv}=(-f\cos v,-f\sin v,0) \]

より、

\[ L=\mathbf{n}\cdot \mathbf{p}_{uu}=\frac{-f^{\prime\prime}g’+f’g^{\prime\prime}}{\sqrt{\varphi}}, \quad M=\mathbf{n}\cdot \mathbf{p}_{uv}=0, \quad N=\mathbf{n}\cdot \mathbf{p}_{vv}=\frac{fg’}{\sqrt{\varphi}} \]

よって、

$$ \begin{align} \begin{pmatrix} E & F \\ F & G \end{pmatrix}^{-1}\begin{pmatrix} L & M \\ M & N \end{pmatrix}&=\frac{1}{EG}\begin{pmatrix} G & 0 \\ 0 & E \end{pmatrix}\begin{pmatrix} L & 0 \\ 0 & M \end{pmatrix} \\ &=\frac{1}{EG}\begin{pmatrix} GL & 0 \\ 0 & EN \end{pmatrix} \end{align} $$

より、曲線・曲面論09の定理2を用いると、平均曲率 \( H \) とガウス曲率 \( K \) は次のようになる。

\[ \begin{align} H&=\frac{1}{2}\text{tr}\left\{ \frac{1}{EG}\begin{pmatrix} GL & 0 \\ 0 & EN \end{pmatrix} \right\}=\frac{1}{2}\left( \frac{L}{E}+\frac{N}{G}\right) \\ &=\frac{1}{2}\left(\frac{-f^{\prime\prime}g’+f’g^{\prime\prime}}{\varphi^{\frac{3}{2}}}+\frac{g’}{f\sqrt{\varphi}}\right), \end{align} \]

\[ K=\det\left\{ \frac{1}{EG}\begin{pmatrix} GL & 0 \\ 0 & EN \end{pmatrix} \right\}=\frac{L}{E}\cdot\frac{N}{G}=\frac{(-f^{\prime\prime}g’+f’g^{\prime\prime})g’}{f\varphi^2} \]

よって、主曲率 \( \kappa_1,\kappa_2 \) は

\[ \kappa_1=\frac{L}{E}=\frac{-f^{\prime\prime}g’+f’g^{\prime\prime}}{\varphi^{\frac{3}{2}}}, \quad \kappa_2=\frac{N}{G}=\frac{g’}{f\sqrt{\varphi}} \]

\( r>0 \) とする。例1で

\[ f(u)=r\sin u, \quad g(u)=r\cos u, \ (0<u<\pi) \]

とおくと、 \( S \) は半径 \( r \) の球面となる。

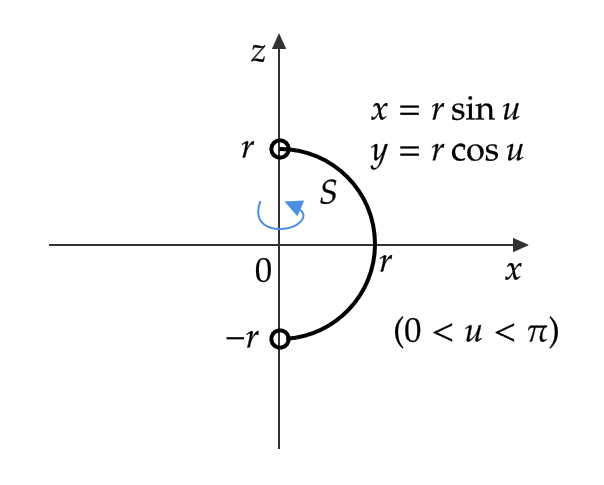
\[ f’=r\cos u=g, \quad f^{\prime\prime}=-r\sin u=-f, \]

\[ g’=-r\sin u=-f, \quad g^{\prime\prime}=-r\cos u=-g \]

したがって、

\[ \varphi=(f’)^2+(g’)^2=g^2+f^2=r^2 \]

であるので、平均曲率 \( H \) とガウス曲率 \( K \) は例1より、

\[ H=\frac{1}{2}\left\{ \frac{-(-f)(-f)+g(-g)}{(r^2)^{\frac{3}{2}}}+\frac{-f}{f\sqrt{r^2}}\right\}=\frac{1}{2}\left(-\frac{1}{r}-\frac{1}{r}\right)=-\frac{1}{r} \]

\[ K=\frac{\{-(-f)(-f)+g(-g)\}(-f)}{fr^4}=\frac{1}{r^2} \]

よって、主曲率 \( \kappa_1,\kappa_2 \) は

\[ \kappa_1=\kappa_2=-\frac{1}{r} \]

一方、

\[ f(u)=r\cos u, \quad g(u)=r\sin u, \ (0<u<\pi) \]

としても \( S \) は半径 \( r \) の球面となる。

このときは、

\[ H=\frac{1}{r}, \quad K=\frac{1}{r^2}, \quad \left(\kappa_1=\kappa_2=\frac{1}{r}\right) \]

例1で

\[ f(u)=u, \quad g(u)=a, \ (u>0) \]

とおくと、 \( S \) は平面となる。

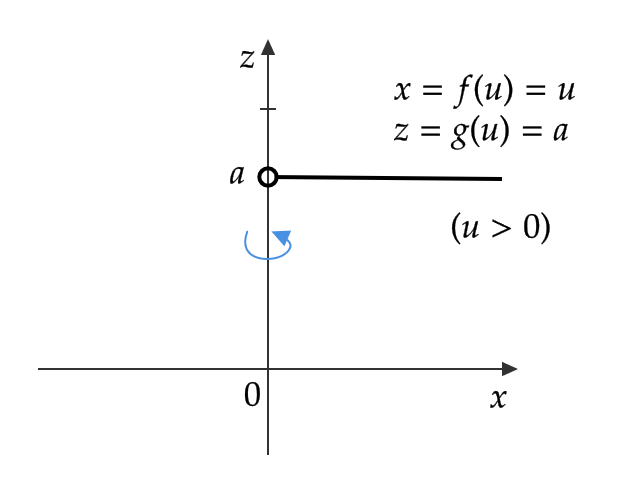
\[ f’=1, \quad f^{\prime\prime}=0, \quad g’=g^{\prime\prime}=0, \quad \varphi=1 \]

したがって、例1より

\[ H=K=0, \quad (\kappa_1=\kappa_2=0) \]

例1で

\[ f(u)=a, \quad g(u)=u, \ (u\in \mathbb{R}) \]

とおくと、 \( S \) は円柱面となる。

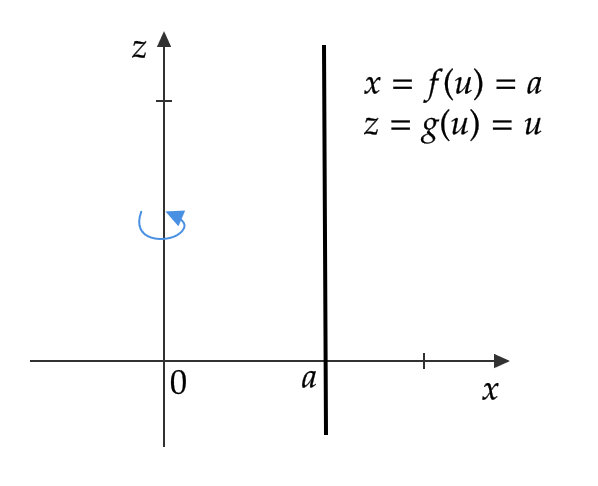
\[ f’=f^{\prime\prime}=0, \quad g’=1, \quad g^{\prime\prime}=0, \quad \varphi=1 \]

したがって、例1より

\[ H=\frac{1}{2a}, \quad K=0, \quad \left(\kappa_1=0, \ \kappa_2=\frac{1}{a}\right) \]

例1で

\[ f(u)=a\cosh \frac{u}{a}, \quad g(u)=u, \ (u\in \mathbb{R}) \]

とする。このとき、 \( S \) を懸垂面という。ただし、 \( \cosh \theta=\frac{e^{\theta}+e^{-\theta}}{2} \)

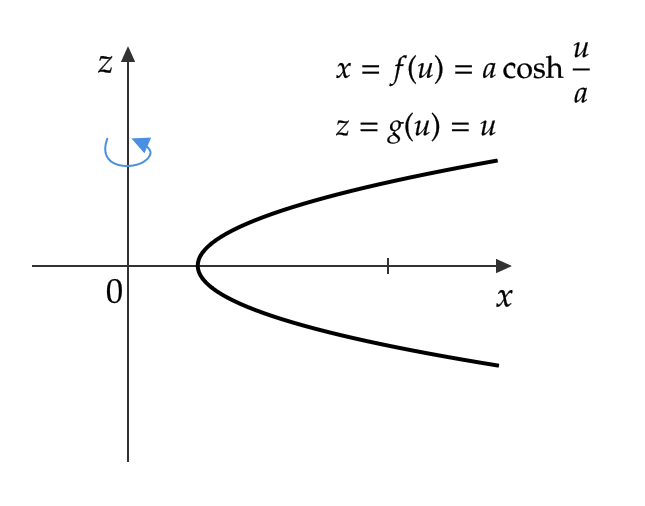
\[ f’=\sinh \frac{u}{a}, \quad f^{\prime\prime}=\frac{1}{a}\cosh \frac{u}{a}=\frac{f}{a^2}, \quad g’=1, \quad g^{\prime\prime}=0, \]

\[ \varphi=\sinh^2\frac{u}{a}+1=\cosh^2\frac{u}{a}=\left(\frac{f}{a}\right)^2 \]

したがって、例1より

\[ H=\frac{1}{2}\left( \frac{-\frac{f}{a^2}\cdot 1+0}{\left\{\left(\frac{f}{a}\right)^2\right\}^{\frac{3}{2}}}+\frac{1}{f\cdot \frac{f}{a}}\right)=\frac{1}{2}\left( -\frac{a}{f^2}+\frac{a}{f^2}\right)=0 \]

\[ K=\frac{-\frac{f}{a^2}\cdot 1+0}{\left\{\left(\frac{f}{a}\right)^2\right\}^{\frac{3}{2}}}+\frac{1}{f\cdot \frac{f}{a}}\cdot \frac{1}{f\cdot \frac{f}{a}}=-\frac{a^2}{f^4} \]

\[ \kappa_1=-\frac{a}{f^2}, \quad \kappa_2=\frac{a}{f^2} \]