こんにちは、ひかりです。
今回は曲線・曲面論から第一基本量と第二基本量を用いた曲率の計算について解説していきます。
この記事では以下のことを紹介します。
- 第一基本量と第二基本量を用いた曲率の計算について
第一基本量と第二基本量を用いた曲率の計算
空間曲面の平均曲率 \( H \) とガウス曲率 \( K \) を第一基本量 \( E,F,G \) と第二基本量 \( L,M,N \) を用いて表現することを考えてみましょう。
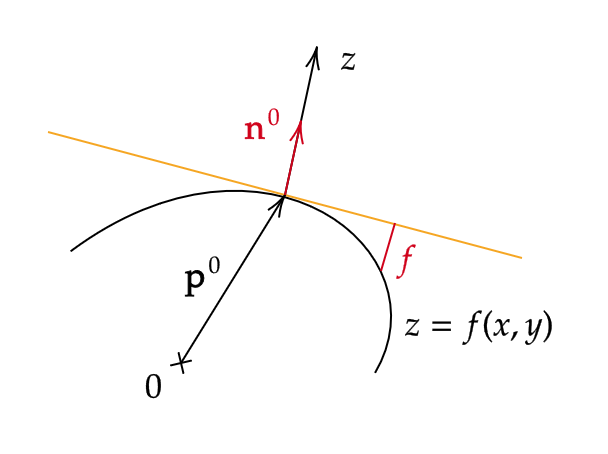
空間曲面 \( S \) 上の点 \( \mathbf{p}(u_0,v_0) \) を考えて、上付き文字0をつけたもので \( (u_0,v_0) \) における値を表すものとします。つまり、
\[ \mathbf{p}^0=\mathbf{p}(u_0,v_0), \quad E^0=E(u_0,v_0) \quad など \]
さらに、 \( \mathbf{p}^0 \) が原点となり、かつ \( \mathbf{p}^0 \) の近傍で曲面 \( S \) が \( z=f(x,y) \) で表され、
\[ f(0,0)=f_x(0,0)=f_y(0,0)=0 \]
となるように \( xyz \) 座標を導入します。
ここで、 \( \mathbf{n}^0=\frac{\mathbf{p}_u^0\times \mathbf{p}_v^0}{\|\mathbf{p}_u^0\times \mathbf{p}_v^0\|} \) とおいて、 \( \mathbf{n}^0 \) 方向に \( z \) 軸をとります。
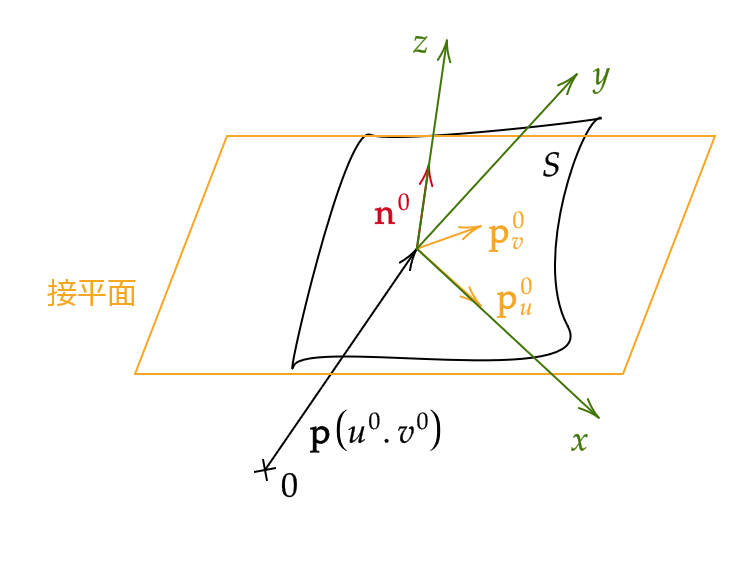
\( x \) 軸、 \( y \) 軸方向の単位ベクトルをそれぞれ \( \mathbf{e}_1,\mathbf{e}_2 \) とおきます。つまり、
\[ \mathbf{e}_1=\frac{\mathbf{p}_u^0}{\|\mathbf{p}_u^0\|}, \quad \mathbf{e}_2=\frac{\mathbf{p}_v^0-(\mathbf{p}_v^0\cdot \mathbf{e}_1)\mathbf{e}_1}{\|\mathbf{p}_v^0-(\mathbf{p}_v^0\cdot \mathbf{e}_1)\mathbf{e}_1\|} \]
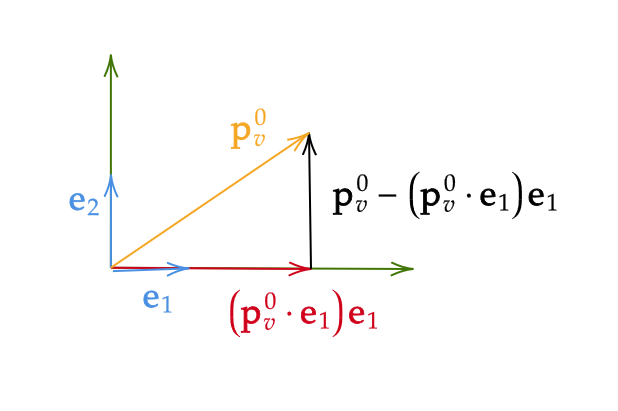
ここで、
\[ \|\mathbf{p}_u^0\|=\sqrt{\mathbf{p}_u^0\cdot\mathbf{p}_u^0}=\sqrt{E^0} \]
より、
\[ \mathbf{e}_1=\frac{\mathbf{p}_u^0}{\|\mathbf{p}_u^0\|}=\frac{\mathbf{p}_u^0}{\sqrt{E^0}} \]
であるので、 \( \mathbf{p}_v^0\cdot \mathbf{p}_u^0=F^0 \) より、
\[ \mathbf{p}_v^0\cdot \mathbf{e}_1=\frac{\mathbf{p}_v^0\cdot \mathbf{p}_u^0}{\sqrt{E^0}}=\frac{F^0}{\sqrt{E^0}} \]
したがって、
\[ \mathbf{p}_v^0-(\mathbf{p}_v^0\cdot \mathbf{e}_1)\mathbf{e}_1=\mathbf{p}_v^0-\frac{F^0}{\sqrt{E^0}}\frac{\mathbf{p}_u^0}{\sqrt{E^0}}=\mathbf{p}_v^0-\frac{F^0}{E^0}\mathbf{p}_u^0 \]
また、
$$ \begin{align} \|\mathbf{p}_v^0-(\mathbf{p}_v^0\cdot \mathbf{e}_1)\mathbf{e}_1\|^2&=\left\|\mathbf{p}_v^0-\frac{F^0}{E^0}\mathbf{p}_u^0\right\|^2=\|\mathbf{p}_v^0\|^2-2\mathbf{p}_v^0\cdot \frac{F^0}{E^0}\mathbf{p}_u^0+\frac{(F^0)^2}{(E^0)^2}\|\mathbf{p}_u^0\|^2 \\ &=G^0-\frac{2(F^0)^2}{E^0}+\frac{(F^0)^2}{E^0}=\frac{E^0G^0-(F^0)^2}{E^0} \end{align} $$
したがって、
\[ \mathbf{e}_2=\sqrt{\frac{E^0}{E^0G^0-(F^0)^2}}\left(\mathbf{p}_v^0-\frac{F^0}{E^0}\mathbf{p}_u^0 \right) \]
\( \{\mathbf{e}_1,\mathbf{e}_2 \} \) で張られる平面上の点は \( \mathbf{p}^0+x\mathbf{e}_1+y\mathbf{e}_2 \) と表されます。
よって、これにより座標 \( (x,y) \) を入れます。
ここで、点 \( (x,y,0) \) を通り \( z \) 軸に平行な直線と曲面 \( S \) との共有点を考えます。
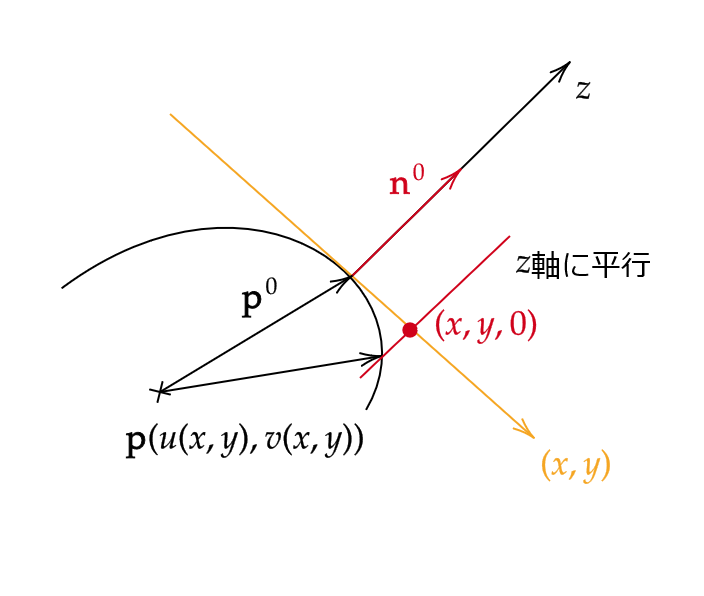
\( x=y=0 \) の近傍では共有点は1つであるので、これを \( \mathbf{p}(u(x,y),v(x,y)) \) とおくことにより、 \( u(x,y),v(x,y) \) を定義することができます。
対応 \( (x,y)\mapsto (u,v) \) は逆対応をもつので、それを \( x=x(u,v),y=y(u,v) \) とおきます。
点 \( (x(u,v),y(u,v)) \) は \( \mathbf{p}(u,v)-\mathbf{p}^0 \) の \( xy \) 平面への直交射影であるので、
\[ x(u,v)=(\mathbf{p}(u,v)-\mathbf{p}^0)\mathbf{e}_1, \quad y(u,v)=(\mathbf{p}(u,v)-\mathbf{p}^0)\mathbf{e}_2 \]
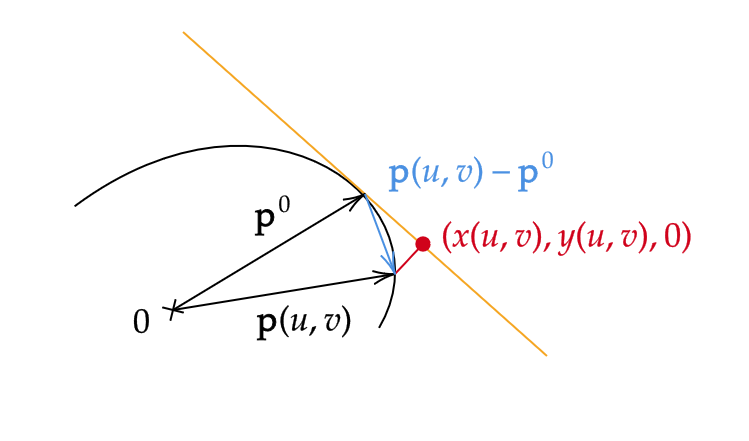
\[ f(x,y)=(\mathbf{p}(u(x,y),v(x,y))-\mathbf{p}^0)\cdot \mathbf{n}^0 \]
とおきます。すると、曲面 \( S \) は \( x=y=z=0 \) の近傍で \( z=f(x,y) \) のグラフとなり
\[ f(0,0)=f_x(0,0)=f_y(0,0)=0 \]
をみたします。
これらを用いて
\[ H=\frac{1}{2}(f_{xx}(0,0)+f_{yy}(0,0)), \quad K=f_{xx}(0,0)f_{yy}(0,0)-(f_{xy}(0,0))^2 \]
を求めます。
\[ f_x=(\mathbf{p}_uu_x+\mathbf{p}_vv_x)\cdot \mathbf{n}^0, \quad f_y=(\mathbf{p}_uu_y+\mathbf{p}_vv_y)\cdot \mathbf{n}^0, \]
\[ f_{xx}=(\mathbf{p}_{uu}u_x^2+2\mathbf{p}_{uv}u_xv_x+\mathbf{p}_{vv}v_x^2+\mathbf{p}_uu_{xx}+\mathbf{p}_vv_{xx})\cdot \mathbf{n}^0, \]
\[ f_{xy}=\{ \mathbf{p}_{uu}u_xu_y+\mathbf{p}_{uv}(u_xv_y+u_yv_x)+\mathbf{p}_{vv}v_xv_y+\mathbf{p}_uu_{xy}+\mathbf{p}_vv_{xy}\}\cdot \mathbf{n}^0, \]
\[ f_{yy}=(\mathbf{p}_{uu}u_y^2+2\mathbf{p}_{uv}u_yv_y+\mathbf{p}_{vv}v_y^2+\mathbf{p}_uu_{yy}+\mathbf{p}_vv_{yy})\cdot \mathbf{n}^0, \]
\[ \mathbf{p}^0_{uu}\cdot \mathbf{n}^0=L^0, \ \mathbf{p}_{uv}^0\cdot \mathbf{n}^0=M^0, \ \mathbf{p}_{vv}^0\cdot\mathbf{n}^0=N^0, \ \mathbf{p}_u^0\cdot \mathbf{n}^0=0, \ \mathbf{p}_v^0\cdot\mathbf{n}^0=0 \]
あと、 \( u_x(0,0),u_y(0,0),v_x(0,0),v_y(0,0) \) を求めればよい。
\[ \begin{pmatrix} u_x(0,0) & u_y(0,0) \\ v_x(0,0) & v_y(0,0) \end{pmatrix}=\begin{pmatrix} x_u^0 & x_v^0 \\y_u^0 & y_v^0 \end{pmatrix}^{-1} \]
であるので、 \( x_u=\mathbf{p}_u\mathbf{e}_1 \) より、
\[ x_u^0=\mathbf{p}_u^0\cdot\mathbf{e}_1^0=\mathbf{p}_u^0\cdot\frac{\mathbf{p}_u^0}{\sqrt{E^0}}=\frac{E^0}{\sqrt{E^0}}=\sqrt{E^0} \]
同様に
\[ x_v^0=\frac{F^0}{\sqrt{E^0}}, \quad y_u^0=0, \quad y_v^0=\sqrt{\frac{E^0G^0-(F^0)^2}{E^0}} \]
であるので、
\[ \begin{pmatrix} u_x(0,0) & u_y(0,0) \\ v_x(0,0) & v_y(0,0) \end{pmatrix}=\begin{pmatrix} x_u^0 & x_v^0 \\y_u^0 & y_v^0 \end{pmatrix}^{-1}=\frac{1}{\sqrt{E^0(E^0G^0-(F^0)^2)}}\begin{pmatrix} \sqrt{E^0G^0-(F^0)^2} & -F^0 \\ 0 & E^0 \end{pmatrix} \]
したがって、
\[ \mathbf{n}^0\cdot \mathbf{p}_{uu}^0=L^0, \ u_x(0,0)=\frac{1}{\sqrt{E^0}}, \ v_x(0,0)=0, \ \mathbf{n}^0\cdot \mathbf{p}_u^0=\mathbf{n}^0\cdot \mathbf{p}_v^0=0 \]
より、
$$ \begin{align} f_{xx}(0,0)&=\mathbf{n}^0\cdot (\mathbf{p}_{uu}^0u_x^2(0,0)+2\mathbf{p}_{uv}^0u_x(0,0)v_x(0,0)+\mathbf{p}_{vv}^0v_x^2(0,0) \\ & \quad \quad +\mathbf{p}_u^0u_{xx}(0,0)+\mathbf{p}_v^0v_{xx}(0,0)) \\ &=\frac{L^0}{E^0} \end{align} $$
同様に
$$ f_{xy}(0,0)=\frac{-F^0L^0+E^0M^0}{E^0\sqrt{E^0G^0-(F^0)^2}}, \quad f_{yy}(0,0)=\frac{(F^0)^2L^0-2E^0F^0M^0+(E^0)^2N^0}{E^0(E^0G^0-(F^0)^2)} $$
したがって、
$$ 2H^0=f_{xx}(0,0)+f_{yy}(0,0)=\frac{G^0L^0-2F^0M^0+E^0N^0}{E^0G^0-(F^0)^2} $$
$$ K^0=f_{xx}(0,0)f_{yy}(0,0)-(f_{xy}(0,0))^2=\frac{L^0N^0-(M^0)^2}{E^0G^0-(F^0)^2} $$
となります。まとめると、
また、主曲率を \( \kappa_1,\kappa_2 \) とすると、
\[ \kappa_1+\kappa_2=2H, \quad \kappa_1\kappa_2=K \]
であるので、
$$ \begin{align} \lambda^2-2H\lambda +K=0の解&\iff (EG-F^2)\lambda^2-(GL-2FM+EN)\lambda+LN-M^2=0 \\ &\iff (L-\lambda E)(N-\lambda G)-(M-\lambda F)^2=0 \\ &\iff \det\left\{\begin{pmatrix} L & M \\ M & N \end{pmatrix}-\lambda\begin{pmatrix} E & F \\ F & G \end{pmatrix}\right\}=0 \end{align} $$
したがって、 \( \det\left\{ \begin{pmatrix} E & F \\ F & G \end{pmatrix}^{-1}\right\} \) を最後の式の両辺にかけると、次のことが成り立ちます。
主曲率は \( \lambda \) に関する2次方程式
\[ \det\left\{\begin{pmatrix} E & F \\ F & G \end{pmatrix}^{-1}\begin{pmatrix} L & M \\ M & N \end{pmatrix}-\lambda I\right\}=0 \]
の解で与えられる。ここで、 \( I \) は2次単位行列である。さらに、平均曲率 \( H \) とガウス曲率 \( K \) は次で与えられる。
\[ H=\frac{1}{2}\text{tr}\left\{ \begin{pmatrix} E & F \\ F & G \end{pmatrix}^{-1}\begin{pmatrix} L & M \\ M & N \end{pmatrix}\right\}, \quad K=\det\left\{ \begin{pmatrix} E & F \\ F & G \end{pmatrix}^{-1}\begin{pmatrix} L & M \\ M & N \end{pmatrix}\right\} \]
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

