こんにちは、ひかりです。
今回は曲線・曲面論から第一基本量と第一基本形式について解説していきます。
この記事では以下のことを紹介します。
- 第一基本量と第一基本形式について
第一基本量と第一基本形式
曲面 \( S \) が位置ベクトル \( \mathbf{p}(u,v) \) で表されているとします。つまり、
$$ S=\{\mathbf{p}(u,v)=(x(u,v),y(u,v),z(u,v)) \ | \ (u,v)\in M \} $$
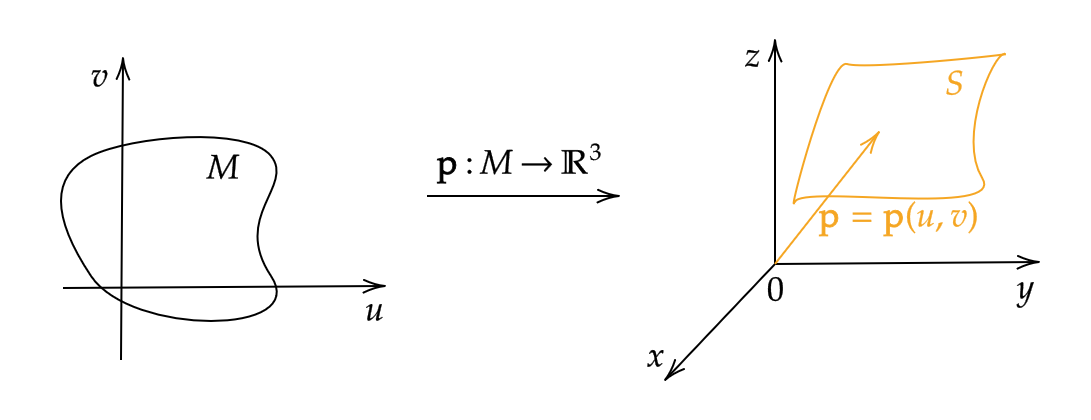
以降、 \( \mathbf{p}_u,\mathbf{p}_v \) でそれぞれの変数による偏導関数を表すことにします。すると、
$$ \mathbf{p}_u=(x_u,y_u,z_u), \ \mathbf{p}_v=(x_v,y_v,z_v) $$
であり、 \( \mathbf{p}_u,\mathbf{p}_v \) はともに \( S \) の接ベクトルになります。
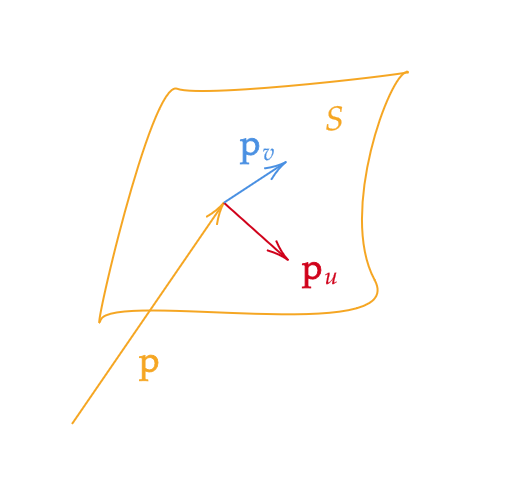
ここで、次に注意します。
$$ \begin{align} &|\mathbf{p}(u+\Delta u,v+\Delta v)-\mathbf{p}(u,v)|^2 \\ &\sim |\mathbf{p}_u\Delta u+\mathbf{p}_v\Delta v|^2 \\ &=(\mathbf{p}_u\cdot \mathbf{p}_u)(\Delta u)^2+2(\mathbf{p}_u\cdot \mathbf{p}_v)\Delta u\Delta v+(\mathbf{p}_v\cdot \mathbf{p}_v)(\Delta v)^2 \end{align} $$
そこで、次を定義します。
$$ \begin{align} E(u,v)&=\mathbf{p}_u(u,v)\cdot \mathbf{p}_u(u,v) \\ F(u,v)&=\mathbf{p}_u(u,v)\cdot \mathbf{p}_v(u,v) \\ G(u,v)&=\mathbf{p}_v(u,v)\cdot \mathbf{p}_v(u,v) \end{align} $$
を曲面 \( S \) の第一基本量という。また、
$$ I(u,v)=E(u,v)du^2+2F(u,v)dudv+G(u,v)dv^2 $$
を曲面 \( S \) の第一基本形式という。
次の位置ベクトルで表現される \( S \) 上の曲線を考える。
$$ \widetilde{\mathbf{p}}(t)=\mathbf{p}(u(t),v(t)) \quad (\alpha≦t≦\beta) $$
(ただし、 \( S \) は \( \mathbf{p}(u,v) \) で表現されているとする)
$$ \frac{d\widetilde{\mathbf{p}}}{dt}=\mathbf{p}_u\frac{du}{dt}+\mathbf{p}_v\frac{dv}{dt} $$
より、
$$ \begin{align} \left\| \frac{d\widetilde{\mathbf{p}}}{dt}\right\|^2&=\frac{d\widetilde{\mathbf{p}}}{dt}\cdot \frac{d\widetilde{\mathbf{p}}}{dt}=\left( \mathbf{p}_u\frac{du}{dt}+\mathbf{p}_v\frac{dv}{dt}\right)\cdot \left( \mathbf{p}_u\frac{du}{dt}+\mathbf{p}_v\frac{dv}{dt}\right) \\ &=E\left( \frac{du}{dt}\right)^2+2F\frac{du}{dt}\frac{dv}{dt}+G\left( \frac{dv}{dt}\right)^2 \end{align} $$
となるので、曲線の長さはベクトル解析03の定理1より、
$$ \int_{\alpha}^{\beta}\left\| \frac{d\widetilde{\mathbf{p}}}{dt}\right\|dt=\int_{\alpha}^{\beta}\sqrt{E\left( \frac{du}{dt}\right)^2+2F\frac{du}{dt}\frac{dv}{dt}+G\left( \frac{dv}{dt}\right)^2}dt $$
$$ S=\{\mathbf{p}(u,v)=(x(u,v),y(u,v),z(u,v)) \ | \ (u,v)\in M \} $$
として、
$$ \mathbf{p}(D)=\{\mathbf{p}(u,v) \ | \ (u,v)\in D \}\subset S $$
とする。このとき、 \( \mathbf{p}(D) \) の面積を求める。
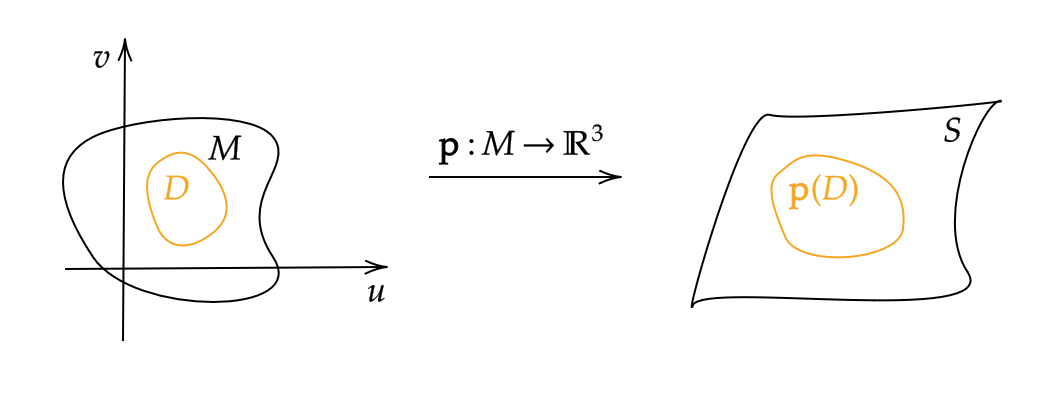
\( \Delta u>0, \ \Delta v>0 \) として、
$$ \Delta S=\{\mathbf{p}(\sigma,\tau) \ | \ u≦\sigma≦u+\Delta u, \ v≦\tau≦v+\Delta v \} $$
とおく。このとき、
$$ \mathbf{a}=\mathbf{p}(u+\Delta u,v)-\mathbf{p}(u,v) $$
$$ \mathbf{b}=\mathbf{p}(u,v+\Delta v)-\mathbf{p}(u,v) $$
とおくと、
$$ \Delta Sの面積=\|\mathbf{a}\times\mathbf{b}\|+o(\Delta u\Delta v) $$
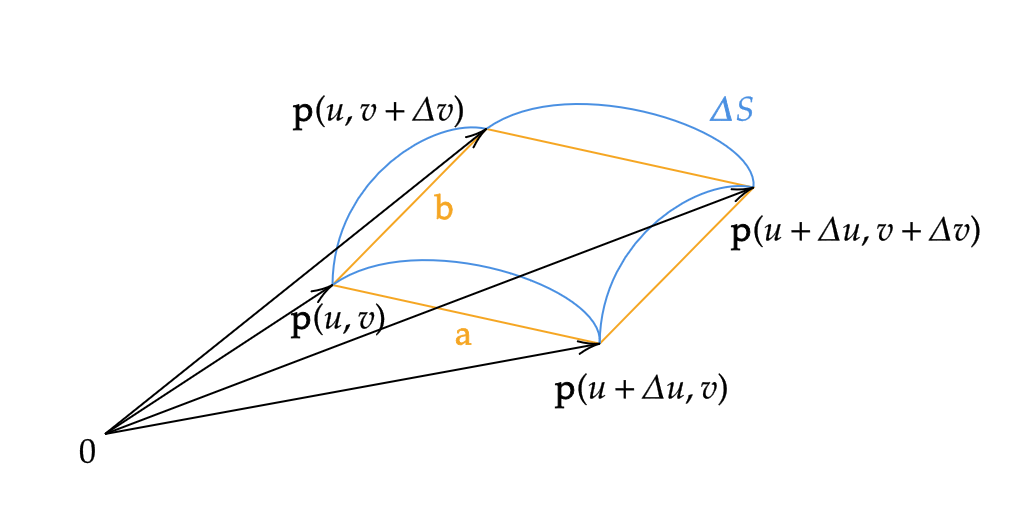
ここで、
$$ \mathbf{a}=\mathbf{p}_u(u,v)\Delta u+o(\Delta u) $$
$$ \mathbf{b}=\mathbf{p}_v(u,v)\Delta v+o(\Delta v) $$
と表せるので、
$$ \Delta S=\|\mathbf{p}_u\times \mathbf{p}_v\|\Delta u\Delta v+o(\Delta u\Delta v) $$
よって、 \( \Delta u\to +0, \ \Delta v\to +0 \) とすると、
$$ dS=\|\mathbf{p}_u\times \mathbf{p}_v\|dudv $$
ここで、ラグランジュの公式
$$ (\mathbf{w}\times \mathbf{x})\cdot (\mathbf{y}\times \mathbf{z})=(\mathbf{w}\cdot \mathbf{y})(\mathbf{x}\cdot \mathbf{z})-(\mathbf{w}\cdot \mathbf{z})(\mathbf{x}\cdot \mathbf{y}) $$
において、 \( \mathbf{w}=\mathbf{y}=\mathbf{p}_u, \ \mathbf{x}=\mathbf{z}=\mathbf{p}_v \) を代入すると、
$$ \|\mathbf{p}_u\times \mathbf{p}_v\|^2=(\mathbf{p}_u\cdot \mathbf{p}_u)(\mathbf{p}_v\cdot\mathbf{p}_v)-(\mathbf{p}_u\cdot\mathbf{p}_v)^2=EG-F^2 \tag{1} $$
より、
$$ \mathbf{p}(D)の面積=\iint_DdS=\iint_D\sqrt{EG-F^2}dudv $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

