こんにちは、ひかりです。
今回は曲線・曲面論から空間曲面の曲率の定義について解説していきます。
この記事では以下のことを紹介します。
- 空間曲面の曲率の定義について
- 平均曲率とガウス曲率について
空間曲面の曲率の定義
今までの記事にて平面及び空間の曲線について見ていきました。
ここからは、空間の曲面について考えていきましょう。
\( S\subset \mathbb{R}^3 \) を滑らかな曲面とします。
この曲面 \( S \) の表示方法としては以下の4つが考えられます。
- 関数 \( z=f(x,y) \) のグラフ
- ベクトル値関数 \( \mathbf{p}(u,v) \) の終点の集合(位置ベクトル)
- 3つの2変数関数 \( x=x(u,v),y=y(u,v),z=z(u,v) \)
- 陰関数表示 \( F(x,y,z)=0 \)
この曲面 \( S \) に対して曲線のときと同様に曲率を定義していきます。
では、平面曲線の曲率の定義と同じようにして、空間曲面を球面で2次近似することはできるのでしょうか。
これは一般にはできません!次の例をご覧ください。
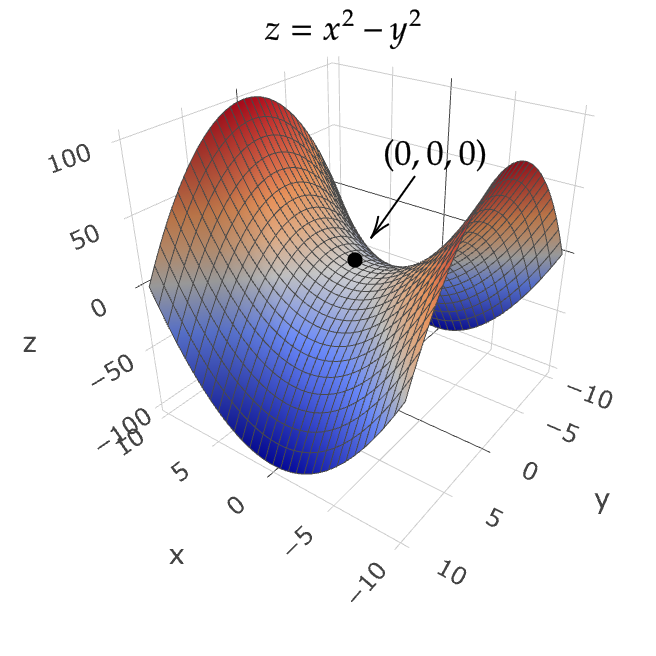
次の空間曲面を考える。
$$ z=x^2-y^2 $$
この曲面は原点において、 \( x \) 軸方向には下に凸、 \( y \) 軸方向には上に凸となる。
したがって、球面では2次近似できない。
そこで、曲面を2次曲面で近似することにより曲率を定義していきましょう。
ここでは、 \( S \) は \( z=f(x,y) \) のグラフで表されているとして \( f \) を \( C^2\)-級であるとします。
このグラフは座標系の回転と平行移動により、次をみたすとしても問題ありません。
$$ f(0,0)=f_x(0,0)=f_y(0,0)=0 $$
このとき、原点を中心とするテイラー展開は
$$ \begin{align} f(x,y)&=\frac{1}{2}(f_{xx}(0,0)x^2+2f_{xy}(0,0)xy+f_{yy}(0,0)y^2)+o(x^2+y^2) \\ &=\frac{1}{2}\begin{pmatrix} x & y \end{pmatrix} \text{Hess} \ f(0,0)\begin{pmatrix} x \\ y \end{pmatrix}+o(x^2+y^2) \end{align} $$
ここで、 \( o \) はスモール・オーダーであり、
$$ \text{Hess} \ f(0,0)=\begin{pmatrix} f_{xx}(0,0) & f_{xy}(0,0) \\ f_{yx}(0,0) & f_{yy}(0,0) \end{pmatrix} $$
はヘッセ行列といわれるものです。
\( f \) が \( C^2\)-級より、このヘッセ行列は実対称行列となるので、適当な \( 2\times 2 \) 直交行列 \( Q \) を用いて、
$$ Q^{-1}\text{Hess} \ f(0,0)Q=\begin{pmatrix} \kappa_1 & 0 \\ 0 & \kappa_2 \end{pmatrix} $$
と \( \text{Hess} \ f(0,0) \) の固有値 \( \kappa_1,\kappa_2 \) にて対角化することができます。
\( Q=\begin{pmatrix} \mathbf{q}_1 & \mathbf{q}_2 \end{pmatrix} \) とおくと、
$$ Q:直交行列 \ \iff \ Q{}^tQ=E \ \iff \ \mathbf{q}_i\cdot \mathbf{q}_j=\delta_{ij}=\begin{cases} 1 & (i=j) \\ 0 & (i\not=j) \end{cases} $$
したがって、 \( \|\mathbf{q}_1\|=1 \) であるので \( \mathbf{q}_1=\begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \) と表すことができます。
同様にして \( \|\mathbf{q}_2\|=1 \) かつ \( \mathbf{q}_1\perp \mathbf{q}_2 \) であるので、
$$ \mathbf{q}_2=\begin{pmatrix} -\sin \theta \\ \cos \theta \end{pmatrix} \ または \ \begin{pmatrix} \sin \theta \\ -\cos \theta \end{pmatrix} $$
どちらを選んでも \( Q^{-1}\text{Hess} \ f(0,0)Q \) は変わらないので、 \( \mathbf{q}_2=\begin{pmatrix} -\sin \theta \\ \cos \theta \end{pmatrix} \) とします。つまり、
$$ Q=\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} $$
となり、これは回転を表す行列となります。
ここで、 \( \begin{pmatrix} \xi \\ \eta \end{pmatrix}=Q^{-1}\begin{pmatrix} x \\ y \end{pmatrix} \) とおくと、 \( \begin{pmatrix} x \\ y \end{pmatrix}=Q\begin{pmatrix} \xi \\ \eta \end{pmatrix} \) となります。このとき、
$$ \begin{align} \begin{pmatrix} x & y \end{pmatrix}\text{Hess} \ f(0,0)\begin{pmatrix} x \\ y \end{pmatrix}&=\begin{pmatrix} \xi & \eta \end{pmatrix}{}^tQ\text{Hess} \ f(0,0)Q\begin{pmatrix} \xi \\ \eta \end{pmatrix} \\ &=\begin{pmatrix} \xi & \eta \end{pmatrix}Q^{-1}\text{Hess} \ f(0,0)Q\begin{pmatrix} \xi \\ \eta \end{pmatrix} \\ &=\begin{pmatrix} \xi & \eta \end{pmatrix}\begin{pmatrix} \kappa_1 & 0 \\ 0 & \kappa_2 \end{pmatrix}\begin{pmatrix} \xi \\ \eta \end{pmatrix}=\kappa_1\xi^2+\kappa_2\eta^2 \end{align} $$
したがって、
$$ f(x,y)=\frac{1}{2}(\kappa_1\xi^2+\kappa_2\eta^2)+o(x^2+y^2)=\frac{1}{2}(\kappa_1\xi^2+\kappa_2\eta^2)+o(\xi^2+\eta^2) $$
となり、 \( z=\frac{1}{2}(\kappa_1\xi^2+\kappa_2\eta^2) \) は点 \( (0,0,0) \) において \( S \) を2次近似しています。
したがって、次のように曲率を定義します。
\( \kappa_1,\kappa_2 \) を \( S \) の点 \( (0,0,0) \) における主曲率という。
また、 \( \xi \) 軸と \( \eta \) 軸の方向を主曲率方向という。
平均曲率とガウス曲率
\( \kappa_1,\kappa_2 \) は \( \text{Hess} \ f(0,0) \) の固有値であるので、
$$ \text{det}(\text{Hess} \ f(0,0)-\lambda E)=0 $$
の解となります。よって、解と係数の関係より、
$$ \kappa_1+\kappa_2=\text{tr} \ \text{Hess} \ f(0,0)=f_{xx}(0,0)+f_{yy}(0,0)=\Delta f(0,0) $$
$$ \kappa_1\kappa_2=\text{det} \ \text{Hess} \ f(0,0)=f_{xx}(0,0)f_{yy}(0,0)-f_{xy}(0,0)^2 $$
となります。
ここで、次を定義します。
\( H=\frac{\kappa_1+\kappa_2}{2} \) を平均曲率、 \( K=\kappa_1\kappa_2 \) をガウス曲率という。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

