複素関数論11：複素積分の定積分への応用

\( \displaystyle \int_0^{\infty}\frac{dx}{1+x^4}=\frac{\sqrt{2}}{4}\pi \) を示す。

\( z\in\mathbb{C} \) に対して、 \( \frac{1}{1+z^4} \) を考えて \( R>0 \) に対して、下図の積分路 \( C_1:t \ (t:-R\to R) \) と \( C_2:Re^{i\theta} \ (\theta:0\to \pi) \) を考える。

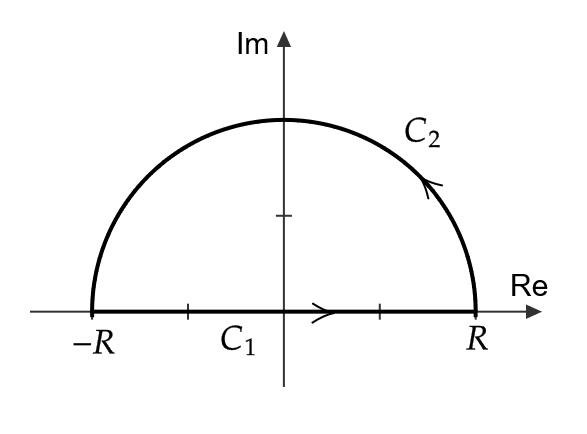
\( R>2 \) に対して、複素関数論09の例1とコーシーの積分定理より、

\[ \int_{C_1+C_2}\frac{dz}{1+z^4}=\frac{\sqrt{2}}{2}\pi \tag{1} \]

まず \( C_1 \) の積分を考えると、

\[ \begin{align} \int_{C_1}\frac{dz}{1+z^4}&=\int_{-R}^R\frac{dt}{1+t^4}=2\int_0^R\frac{dt}{1+t^4} \quad (偶関数より) \\ &\to 2\int_0^{\infty}\frac{dt}{1+t^4} \quad (R\to \infty) \end{align} \]

次に \( C_2 \) の積分を評価する。

\[ \begin{align} \left| \int_{C_2}\frac{dz}{1+z^4}\right|&=\left|\int_0^{\pi}\frac{1}{1+R^4e^{4i\theta}}(Re^{i\theta})’d\theta\right|≦\int_0^{\pi}\left|\frac{iRe^{i\theta}}{1+R^4e^{4i\theta}}\right|d\theta \\ &≦\int_0^{\pi}\frac{R}{|R^4e^{4i\theta}|-1}d\theta=\int_0^{\pi}\frac{R}{R^4-1}d\theta=\frac{\pi R}{R^4-1}\to 0 \ (R\to \infty) \end{align} \]

したがって、式(1)で \( R\to \infty \) とすると、

\[ 2\int_0^{\infty}\frac{dt}{1+t^4}=\frac{\sqrt{2}}{2}\pi \]

なので、

\[ \int_0^{\infty}\frac{dx}{1+x^4}=\frac{\sqrt{2}}{4}\pi \]

\( \displaystyle \int_0^{2\pi}\frac{d\theta}{a+b\cos \theta}=\frac{2\pi}{\sqrt{a^2-b^2}} \ (a>b>0) \) を示す。

\( z=i\theta \) とおくと、

\[ \cos \theta=\frac{1}{2}(e^{i\theta}+e^{-i\theta})=\frac{1}{2}\left(z+\frac{1}{z}\right), \quad dz=ie^{i\theta}d\theta=izd\theta \]

より、

\[ \int_0^{2\pi}\frac{d\theta}{a+b\cos \theta}=\int_{\{|z|=1\}}\frac{1}{a+b\left( \frac{1}{2}\left( z+\frac{1}{z}\right)\right)}\frac{1}{iz}dz=\frac{2}{i}\int_{\{|z|=1\}}\frac{dz}{bz^2+2az+b} \]

となる。ここで、 \( bz^2+2az+b=0 \) となる \( z \) は

\[ \alpha_1=\frac{-a+\sqrt{a^2-b^2}}{b}, \quad \alpha_2=\frac{-a-\sqrt{a^2-b^2}}{b} \]

となるが、 \( \alpha_2<-1<\alpha_1<0 \) より、 \( \{|z|=1\} \) の内側で正則でない点は \( \alpha_1 \) のみである。

よって、コーシーの積分定理とコーシーの積分公式より、

\[ \frac{2}{i}\int_{\{|z|=1\}}\frac{dz}{bz^2+2az+b}=\frac{2}{ib}\int_{\{|z|=1\}}\frac{\frac{1}{(z-\alpha_2)}}{z-\alpha_1}dz=\frac{2}{ib}\frac{2\pi i}{\alpha_1-\alpha_2}=\frac{2\pi}{\sqrt{a^2-b^2}} \]

したがって、

\[ \int_0^{2\pi}\frac{d\theta}{a+b\cos \theta}=\frac{2\pi}{\sqrt{a^2-b^2}} \]

\( m\in\mathbb{N} \) に対して、 \( \displaystyle \int_{-\infty}^{\infty}\frac{\cos(mx)}{1+x^2}dx=\pi e^{-m} \) を示す。

\( f(z)=\frac{e^{imz}}{1+z^2} \) を考えると、正則でない点は \( z=\pm i \) となる。

また、 \( R>1 \) に対して、下図の積分路 \( C_1:t \ (t:-R\to R) \) と \( C_2: Re^{i\theta} \ (\theta:0\to \pi) \) を考える。

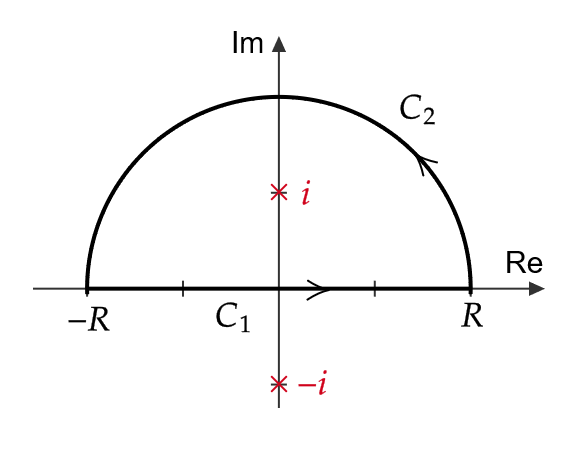
すると、コーシーの積分公式より、

\[ \begin{align} \int_{C_1+C_2}\frac{e^{imz}}{1+z^2}dz&=\int_{C_1+C_2}\frac{\frac{e^{imz}}{z+i}}{z-i}dz=\frac{2\pi ie^{imi}}{i+i}=\pi e^{-m} \end{align} \tag{2} \]

まず \( C_1 \) の積分を考えると、

\[ \begin{align} \int_{C_1}\frac{e^{imz}}{1+z^2}dz&=\int_{-R}^R\frac{e^{imt}}{1+t^2}dt \\ &\to \int_{-\infty}^{\infty}\frac{e^{imt}}{1+t^2}dt=\int_{-\infty}^{\infty}\frac{\cos (mt)}{1+t^2}dt+i\int_{-\infty}^{\infty}\frac{\sin (mt)}{1+t^2}dt \end{align} \]

次に \( C_2 \) の積分を評価する。

\[ \left|\int_{C_2}\frac{e^{imz}}{1+z^2}dz\right|=\left|\int_0^{\pi}\frac{e^{imRe^{i\theta}}}{1+R^2e^{2i\theta}}(Re^{i\theta})’d\theta\right|≦\int_0^{\pi}\frac{R|e^{imRe^{i\theta}}|}{R^2-1}d\theta \]

であり、

\[ |e^{imRe^{i\theta}}|=|e^{imR(\cos\theta+i\sin \theta)}|=|e^{-mR\sin \theta}|≦1 \]

より、

\[ \left|\int_{C_2}\frac{e^{imz}}{1+z^2}dz\right|≦\int_0^{\pi}\frac{R}{R^2-1}d\theta=\frac{\pi R}{R^2-1}\to 0 \quad (R\to \infty) \]

したがって、式(2)で \( R\to \infty \) とすると、

\[ \int_{-\infty}^{\infty}\frac{\cos (mt)}{1+t^2}dt+i\int_{-\infty}^{\infty}\frac{\sin (mt)}{1+t^2}dt=\pi e^{-m} \]

となるので、実部を比較すると、

\[ \int_{-\infty}^{\infty}\frac{\cos(mx)}{1+x^2}dx=\pi e^{-m} \]

\( \displaystyle \int_0^{\infty}\frac{\sin x}{x}dx=\frac{\pi}{2} \) を示す。

\( f(z)=\frac{e^{iz}}{z} \) を考えると、正則でない点は \( z=0 \) となる。

また、 \( R,\varepsilon>0 \) に対して、下図の積分路

\[ \begin{align} C_1& : Re^{i\theta} \ (\theta : 0\to \pi) \quad C_2 : t \ (t : -R\to -\varepsilon) \\ C_3& : \varepsilon e^{i\theta} \ (t : \pi \to 0) \quad C_4 : t \ (t : \varepsilon \to R) \end{align} \]

を考える。

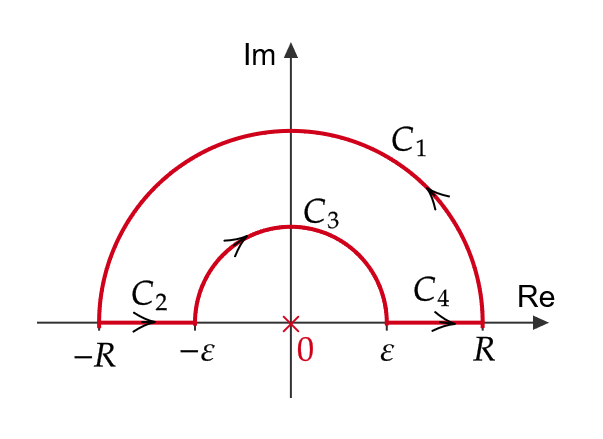
\( \frac{e^{iz}}{z} \) は \( C_1+C_2+C_3+C_4 \) 内で正則であるので、コーシーの積分定理より、

\[ \int_{C_1+C_2+C_3+C_4}\frac{e^{iz}}{z}dz=0 \tag{3} \]

まず \( C_1 \) の積分を評価する。

$$ \begin{align*} \left|\int_{C_1}\frac{e^{iz}}{z}dz\right|&=\left| \int_0^{\pi}\frac{e^{-iRe^{i\theta}}}{Re^{i\theta}}iRe^{i\theta}d\theta\right|≦\int_0^{\pi}|e^{-iRe^{i\theta}}|d\theta \\ &=\int_0^{\pi}e^{-R\sin \theta}d\theta=2\int_0^{\frac{\pi}{2}}e^{-R\sin \theta}d\theta \quad (\sin \thetaの周期性) \\ &≦2\int_0^{\frac{\pi}{2}}e^{-R\left( \frac{2}{\pi}\theta\right)}d\theta \quad (0≦\theta≦2\piのとき\sin\theta≧\frac{2}{\pi}\theta) \\ &=\frac{\pi}{R}(1-e^{-R})\to 0 \quad (R\to \infty) \end{align*} $$

次に \( C_2+C_4 \) の積分を考えると、

$$ \begin{align*} \int_{C_2+C_4}\frac{e^{iz}}{z}dz&=\int_{-R}^{-\varepsilon}\frac{\cos x+i\sin x}{x}dx+\int_{\varepsilon}^R\frac{\cos x+i\sin x}{x}dx \\ &=2i\int_{\varepsilon}^R\frac{\sin x}{x}dx \quad (\frac{\cos x}{x}：奇関数、\frac{\sin x}{x}：偶関数) \end{align*} $$

最後に \( C_3 \) の積分を考えます。

\[ \int_{C_3}\frac{e^{iz}}{z}dz=\int_{C_3}\frac{1}{z}dz+\int_{C_3}\frac{e^{iz}-1}{z}dz \]

に分ける。すると、

\[ \int_{C_3}\frac{1}{z}dz=\int_{\pi}^0\frac{1}{\varepsilon e^{i\theta}}(\varepsilon e^{i\theta})’d\theta=-\pi i \]

となる。一方で、

$$ \begin{align*} |e^{iz}-1|&=\left|\left( 1+\frac{1}{1!}z+\frac{1}{2!}z^2+\cdots+\frac{1}{n!}z^n+\cdots\right)-1\right| \\ &=\left| \frac{1}{1!}z+\frac{1}{2!}z^2+\cdots+\frac{1}{n!}z^n+\cdots\right| \\ &=|z|\left| \frac{1}{1!}+\frac{1}{2!}z+\cdots+\frac{1}{n!}z^{n-1}+\cdots\right| \\ &≦|z|\left( 1+\frac{1}{1!}|z|+\frac{1}{2!}|z|^2+\cdots+\frac{1}{n!}|z|^n+\cdots \right)≦|z|e^{|z|} \end{align*} $$

より、

\[ \left|\int_{C_3}\frac{e^{iz}-1}{z}dz\right|≦\left| \int_{\pi}^0\frac{|\varepsilon e^{i\theta}|e^{|\varepsilon e^{i\theta}|}}{|\varepsilon e^{i\theta}|}|i\varepsilon e^{i\theta}|d\theta\right|=\varepsilon e^{\varepsilon}\pi \to 0 \quad (\varepsilon \to 0) \]

以上により、式(3)で \( R\to \infty, \ \varepsilon \to 0 \) とすると、

\[ 2i\int_0^{\infty}\frac{\sin x}{x}dx-\pi i=0 \]

であるので、

\[ \int_0^{\infty}\frac{\sin x}{x}dx=\frac{\pi}{2} \]