こんにちは、ひかりです。
今回は複素関数論からコーシーの積分定理について解説していきます。
この記事では以下のことを紹介します。
- コーシーの積分定理について
- 曲線の向きと正則でない点を含む複素積分について
コーシーの積分定理
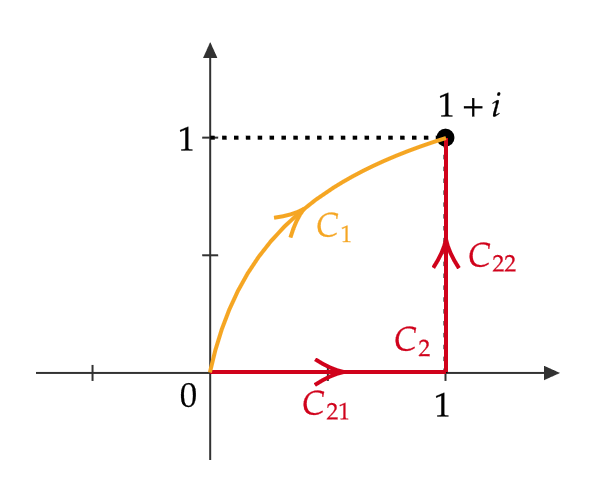
複素関数論07の例2を見ると、始点と終点が同じ2つの異なる積分路 \( C_1,C_2 \) に対して、
\[ \int_{C_1}zdz=\int_{C_2}zdz=i \]
となっています。しかし、これは必ず成り立つとは限りません。
\( \displaystyle \int_C\overline{z}dz \) を始点と終点が同じ2つの異なる積分路 \( C_1,C_2 \) に沿って積分する。
\[ 放物線 \ C_1: z(t)=t^2+ti \ (0≦t≦1) \]
\[ 折れ線 \ C_2: z(t)=\begin{cases} t & (0≦t≦1) \\ 1-i+ti & (1≦t≦2) \end{cases} \]
$$ \begin{align} \int_{C_1}\overline{z}dz&=\int_0^1\overline{z(t)}z'(t)dt=\int_0^1(t^2-ti)(2t+i)dt \\ &=\int_0^1(2t^3+t-t^2i)dt=1-\frac{i}{3} \end{align} $$
また、 \( C_2 \) については
$$ C_{21}: z(t)=t \ (0≦t≦1), \quad C_{22}: z(t)=1-i+ti \ (1≦t≦2) $$
とおくと、 \( C_2=C_{21}+C_{22} \) であるので、
$$ \begin{align} \int_{C_2}\overline{z}dz&=\int_{C_{21}}\overline{z}dz+\int_{C_{22}}\overline{z}dz=\int_0^1\overline{z(t)}z'(t)dt+\int_1^2\overline{z(t)}z'(t)dt \\ &=\int_0^1t\cdot 1dt+\int_1^2(1+i-ti)idt=1+i \end{align} $$
したがって、
\[ \int_{C_1}\overline{z}dz\not=\int_{C_2}\overline{z}dz \]
ではどのようなときに複素積分が積分路に依らずに始点と終点のみにより決まるのでしょうか。
それを見るために、まず次を示します。
\( D\subset \mathbb{C} \) を領域、 \( f:D\to \mathbb{C} \) を \( D \) 上正則、 \( C \) を \( D \) 内の曲線とする。このとき、
\[ f(z)=u(x,y)+iv(x,y) \quad (z=x+iy\in D) \]
とおくと、
\[ \int_Cf(z)dz=\int_C(udx-vdy)+i\int_C(vdx+udy) \]
定理1の証明(気になる方だけクリックしてください)
もう少しお待ちください。
また、次を定義します。
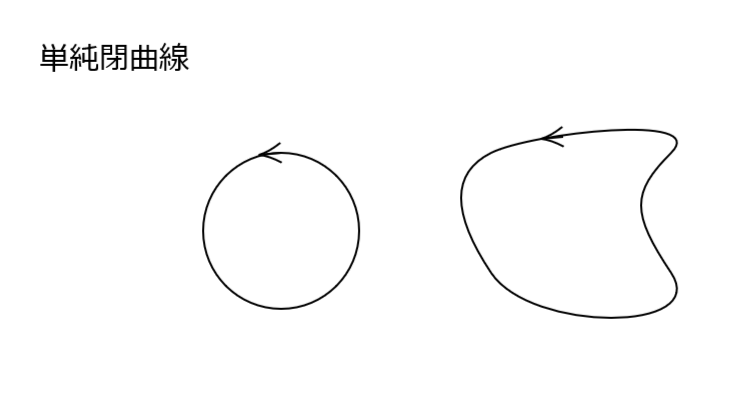
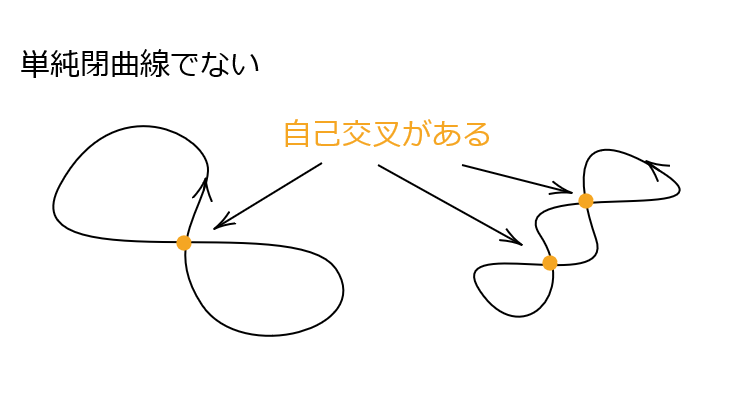
\( C:\varphi(t) \ (a≦t≦b) \) が単純閉曲線であるとは、 \( \varphi(a)=\varphi(b) \) となる \( a<x,y<b \) に対して、
\[ \varphi(x)=\varphi(y) \ \Rightarrow x=y \]
をみたすことをいう。(つまり自己交叉がない閉曲線のことである)
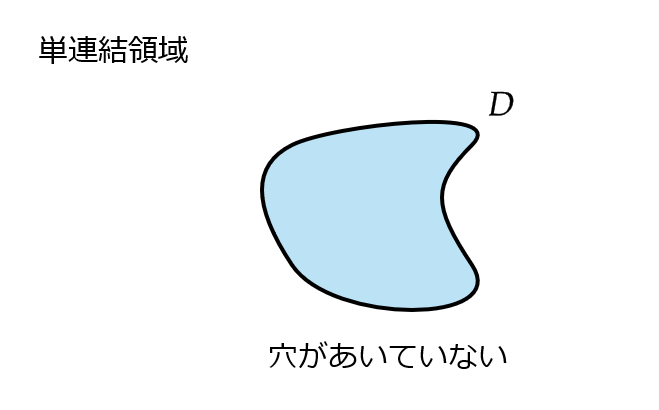
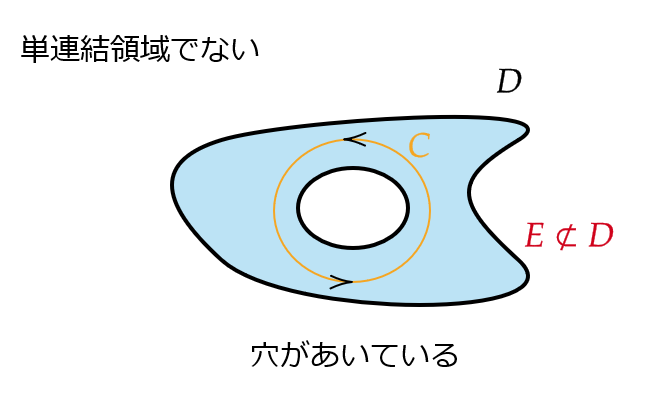
領域 \( D\subset \mathbb{C} \) が単連結領域であるとは次をみたすことをいう。
\( D \) 内の任意の閉曲線 \( C \) に対して、 \( C \) で囲まれた領域を \( E \) とすると、 \( E\subset D \)
(つまり、穴の空いていない領域のことである)
これらの準備のもと、複素積分においてとても重要な定理であるコーシーの積分定理を示すことができます。
\( D\subset \mathbb{C} \) を単連結領域、 \( f:D\to\mathbb{C} \) を \( D \) 上正則、 \( C \) を \( D \) 内の単純閉曲線とする。このとき、
\[ \int_Cf(z)dz=0 \]
定理2の証明(気になる方だけクリックしてください)
もう少しお待ちください。
これを用いて複素積分が積分路に依らずに始点と終点のみにより決まる条件を考えることができます。
\( D\subset \mathbb{C} \) を単連結領域、 \( f:D\to\mathbb{C} \) を \( D \) 上正則、 \( \eta,z\in D \) 、 \( C_1,C_2 \) を始点 \( \eta \) で終点 \( z \) の曲線とする。このとき、
\[ \int_{C_1}f(w)dw=\int_{C_2}f(w)dw \]
定理3の証明(気になる方だけクリックしてください)
もう少しお待ちください。
曲線の向きと正則でない点を含む複素積分
上では \( D\subset \mathbb{C} \) が正則な場合を考えましたが、今度は \( D \) に正則でない点がある場合を見ていきましょう。
そのためにまず曲線の向きというものを考えます。
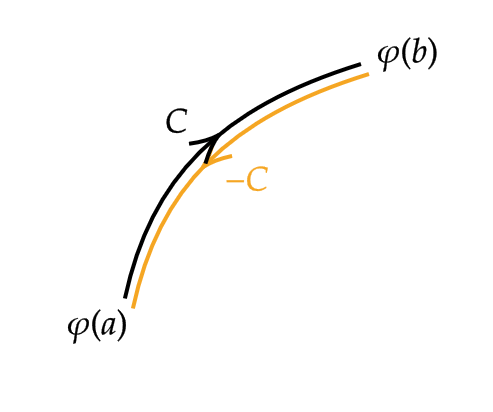
曲線 \( C:\varphi(t) \ (a≦t≦b) \) において向きを強調するときは \( C:\varphi(t) \ (t:a\to b) \) と書きます。
このとき、 \( -C:\varphi(t) \ (t:b\to a) \) となります。
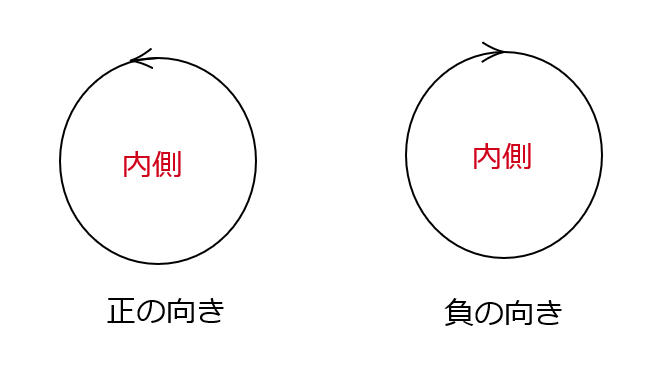
閉曲線の進む向きについては、曲線の内側を左に見て進む向き(反時計回り)を正の向きといいます。
そして、正の向きと反対の向き(時計回り)を負の向きといいます。
以降、話を簡単にするために \( a\in D \) で正則でない場合を考えます。
このとき、次のことが成り立ちます。
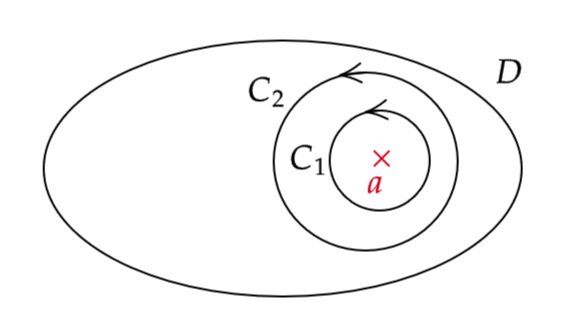
\( D\subset \mathbb{C} \) を単連結領域、 \( a\in D \) で \( f:D\backslash\{a\}\to \mathbb{C} \) は \( D\backslash \{a\} \) 上で正則とする。
また、 \( C_1,C_2 \) を \( D\backslash\{a\} \) 内の互いに交わらない単純閉曲線で \( a \) を曲線の内側に含むとする。このとき、
\[ \int_{C_1}f(z)dz=\int_{C_2}f(z)dz \]
ただし、閉曲線の向きは正の向きとする。
定理4の証明(気になる方だけクリックしてください)
もう少しお待ちください。
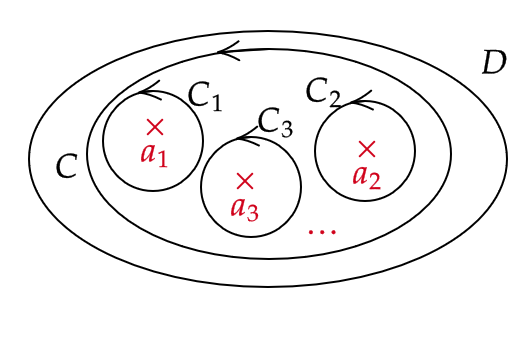
複数正則でない点がある場合は次のようになります。
\( D\subset \mathbb{C} \) を単連結領域、 \( a_1,\cdots,a_n\in D \) で \( f:D\backslash\{a_1,\cdots,a_n\}\to \mathbb{C} \) は \( D\backslash \{a_1,\cdots,a_n\} \) 上で正則とする。
\( C \) を \( D\backslash \{a_1,\cdots,a_n\} \) 上の単純閉曲線で \( a_1,\cdots,a_n \) を内側に含むとする。
\( C_i \) を \( D\backslash \{a_1,\cdots,a_n\} \) 上の単純閉曲線で \( a_i \) を \( C_i \) の内側に含み、他の \( a_j \) を \( C_i \) の内側に含まないとする。
このとき、
\[ \int_Cf(z)dz=\sum_{i=1}^n\int_{C_i}f(z)dz \]
ただし、各閉曲線の向きは正の向きとする。
定理5の証明(気になる方だけクリックしてください)
もう少しお待ちください。
\( \mathbb{C} \) 上の原点中心、半径2の円を \( C=\{z\in\mathbb{C} : |z|=2\} \) とするとき、 \( \displaystyle \int_C\frac{dz}{z(z-1)} \) を求める。
下図のような補助積分路
\[ C_1: \frac{1}{3}e^{i\theta} \ (\theta:0\to 2\pi) \]
\[ C_2:1+\frac{1}{3}e^{i\theta} \ (\theta:0\to2\pi) \]
および \( C’_1,C’_2 \) をとる。
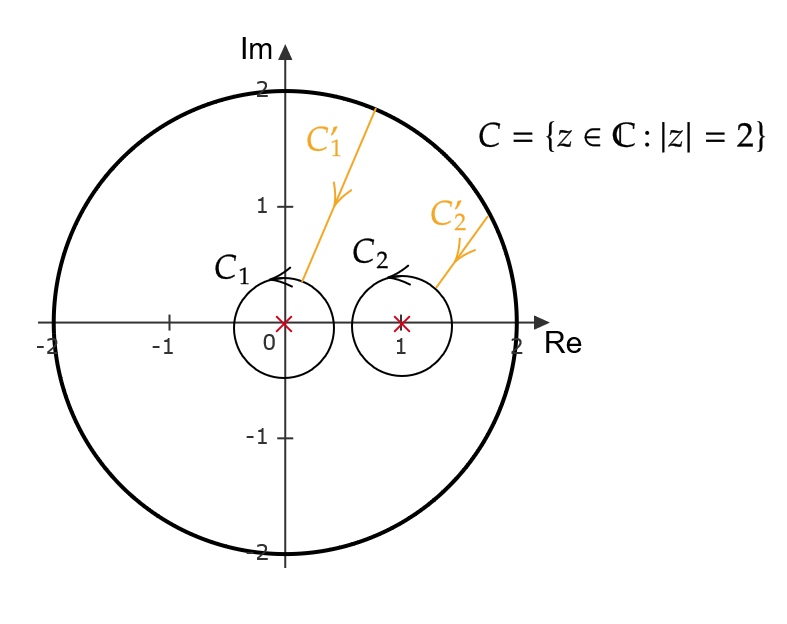
すると、定理5より、
\[ \int_C\frac{dz}{z(z-1)}=\int_{C_1}\frac{dz}{z(z-1)}+\int_{C_2}\frac{dz}{z(z-1)} \]
となるので、
$$ \begin{align} \int_{C_1}\frac{dz}{z(z-1)}&=\int_{C_1}\frac{1}{z-1}dz-\int_{C_1}\frac{1}{z}dz \\ &=-\int_{C_1}\frac{1}{z}dz \quad (コーシーの積分定理より) \\ &=-\int_0^{2\pi}\frac{1}{\frac{1}{3}e^{i\theta}}\left( \frac{1}{3}e^{i\theta}\right)’d\theta=-i\int_0^{2\pi}d\theta=-2\pi i \end{align} $$
$$ \begin{align} \int_{C_2}\frac{dz}{z(z-1)}&=\int_{C_2}\frac{1}{z-1}dz-\int_{C_2}\frac{1}{z}dz \\ &=\int_{C_2}\frac{1}{z-1}dz \quad (コーシーの積分定理より) \\ &=\int_0^{2\pi}\frac{1}{\left(1+\frac{1}{3}e^{i\theta}\right)-1}\left( 1+\frac{1}{3}e^{i\theta}\right)’d\theta=i\int_0^{2\pi}d\theta=2\pi i \end{align} $$
より、
\[ \int_C\frac{dz}{z(z-1)}=-2\pi i+2\pi i=0 \]
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

