こんにちは、ひかりです。
今回は複素関数論から複素数と複素平面について解説していきます。
この記事では以下のことを紹介します。
- 複素数とその演算について
- 複素平面とド・モアブルの定理について
複素数とその演算
\( x,y\in\mathbb{R} \) と虚数単位 \( i=\sqrt{-1} \) によって作られた数 \( z=x+iy \) を複素数といいます。
ここで、 \( i \) は \( i^2=-1 \) をみたします。
また、複素数 \( z=x+iy \) に対して、複素数の実部を \( \text{Re}z=x \) 、虚部を \( \text{Im}z=y \) と定めます。
とくに、 \( \text{Re}z=0 \) となる複素数(つまり、 \( z=iy \) )を純虚数といいます。
さらに、複素数全体の集合を \( \mathbb{C} \) とおきます。
複素数に対しては次のような演算が定められています。
\( z_1=x_1+iy_1,z_2=x_2+iy_2\in\mathbb{C} \) に対して、次のように演算を定める。
$$ z_1=z_2 \ \overset{\text{def}}{\Longleftrightarrow} \ x_1=x_2 \ かつ \ y_1=y_2 $$
$$ z_1+z_2=(x_1+x_2)+i(y_1+y_2) $$
$$ z_1-z_2=(x_1-x_2)+i(y_1-y_2) $$
$$ z_1z_2=(x_1x_2-y_1y_2)+i(x_1y_2+x_2y_1) $$
$$ \frac{z_1}{z_2}=\frac{x_1x_2+y_1y_2}{x_2^2+y_2^2}+i\frac{-x_1y_2+x_2y_1}{x^2_2+y^2_2} \quad (z_2\not=0) $$
複素数 \( z=x+iy\in \mathbb{C} \) に対して、
$$ \overline{z}=\text{Re}z-i\text{Im}z=x-iy\in\mathbb{C} $$
とおきます。この \( \overline{z} \) を \( z \) の共役複素数といいます。
(1) $$ (7-3i)(4+5i)=(28+15)+(35-12)i=43+23i $$
(2) $$ \begin{align} \frac{12+2i}{1+i}&=\frac{2(6+i)(1-i)}{(1+i)(1-i)}=\frac{2(6+i)(1-i)}{1+1} \\ &=(6+i)(1-i)=(6+1)+(1-6)i=7-5i \end{align} $$
(3) \( z^2=-i \) となる \( z\in\mathbb{C} \) を求める。
\( z=x+iy \ (x,y\in\mathbb{R}) \) とおくと、 \( z^2=-i \) より
$$ z^2=(x+iy)^2=(x^2+y^2)+2ixy=-i $$
であるので、
$$ \begin{cases} x^2-y^2=0 \\ 2xy=-1 \end{cases} $$
となる。これを解くと、 \( (x-y)(x+y)=0 \) より、 \( x=y \) または \( x=-y \) となるが、 \( x=y \) は \( 2xy=-1 \) をみたさない。
よって、 \( x=-y, \ -2x^2=-1 \) より、 \( x=\pm\frac{1}{\sqrt{2}}, \ y=\mp\frac{1}{\sqrt{2}} \) (複合同順)となる。
したがって、 \( z=\pm\frac{1}{\sqrt{2}}(1-i) \)
複素平面とド・モアブルの定理
複素平面と極形式
複素数 \( z=x+iy\in\mathbb{C} \) は \( xy \) 平面上の点 \( (x,y) \) として表すことができます。
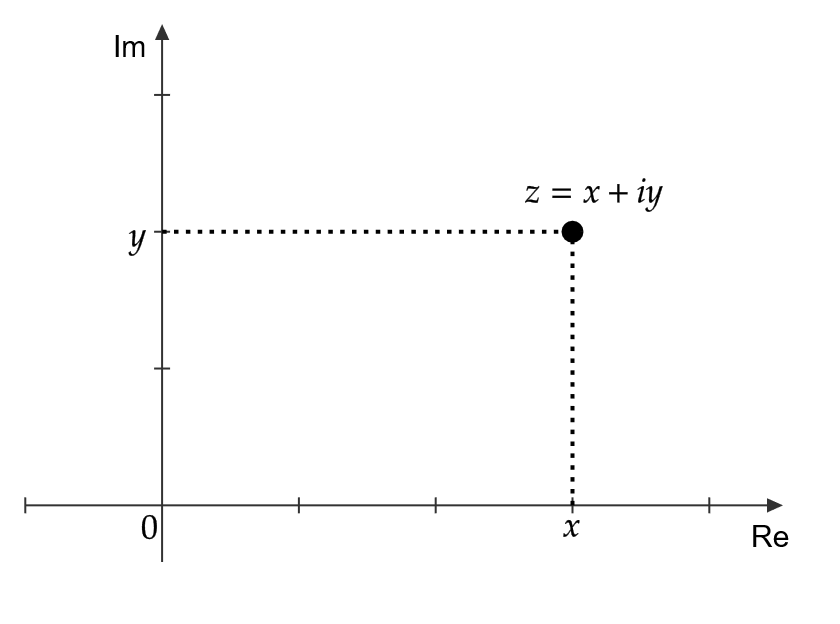
この平面のことを複素平面といい、横軸を実軸、縦軸を虚軸といいます。
複素数 \( z=x+iy\in\mathbb{C} \) を極座標 \( (r,\theta) \) で表すと、
$$ r=\sqrt{x^2+y^2}, \quad \theta=\arctan \frac{y}{x} $$
となります。ただし、 \( \theta \) は1通りに定まりません。(つまり、 \( \pm 2\pi,\pm4\pi, \cdots \) としてもかわりません)
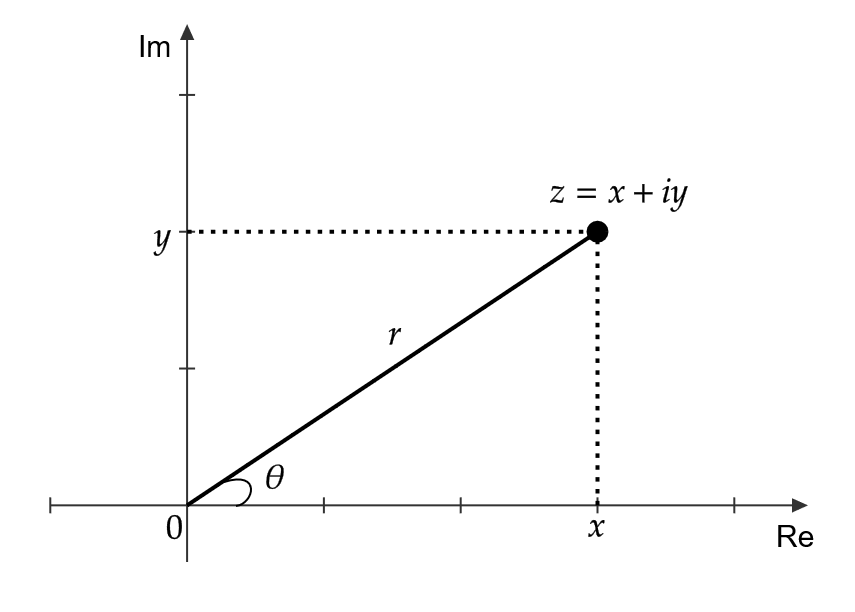
\( r \) を \( z \) の絶対値、 \( \theta \) を偏角といい、
$$ |z|=\sqrt{x^2+y^2}=r, \quad \text{arg} \ z=\theta $$
と表します。このとき、
$$ z=x+iy=r(\cos \theta+\sin\theta) $$
となります。この \( r,\theta \) で書いた式を \( z \) の極形式といいます。
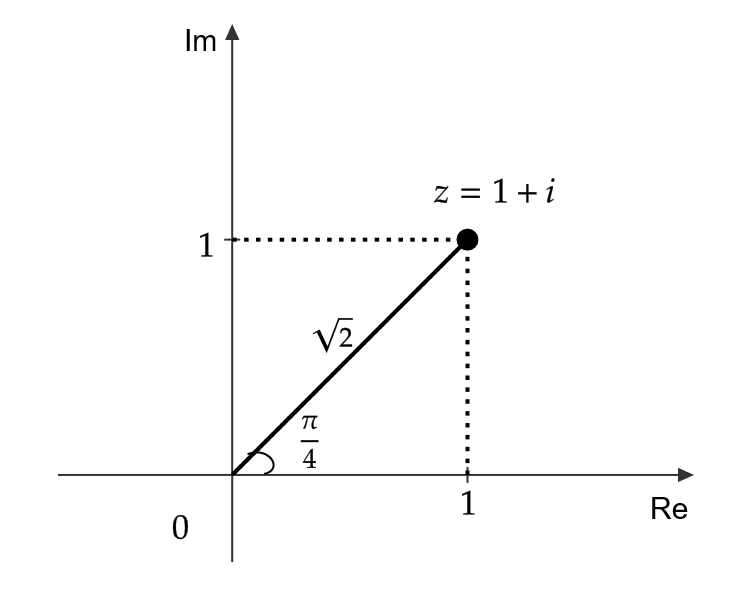
(1) \( 1+i \) の極形式を求める。
\( 1+i \) は複素平面上では \( (1,1) \) の点となるので、下の図から極形式は
$$ 1+i=\sqrt{2}\left(\cos \frac{\pi}{4}+i\sin \frac{\pi}{4}\right) $$
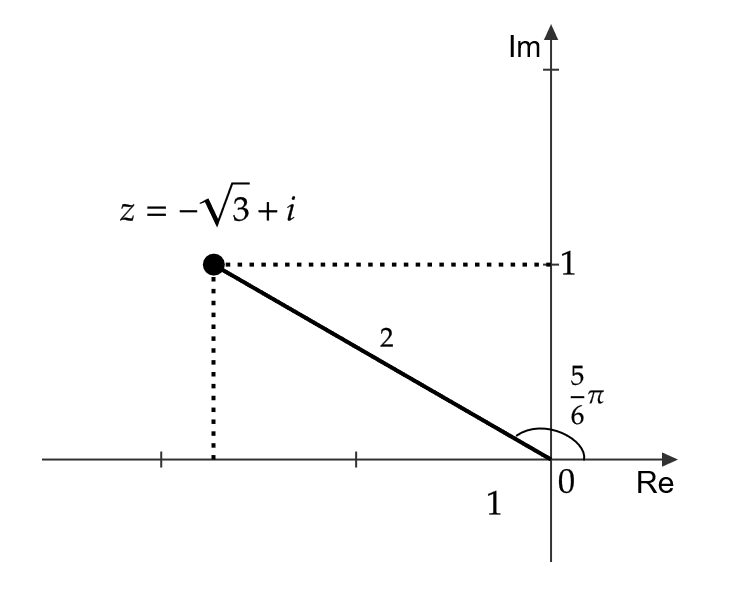
(2) \( -\sqrt{3}+i \) の極形式を求める。
\( -\sqrt{3}+i \) は複素平面上では \( (-\sqrt{3},1) \) の点となるので、下の図から極形式は
$$ -\sqrt{3}+i=2\left(\cos \frac{5}{6}\pi+i\sin \frac{5}{6}\pi\right) $$
複素平面と積
\( z_1,z_2\in\mathbb{C} \) に対して、 \( z_1z_2,\frac{z_1}{z_2} \) を複素平面に図示してみましょう。
簡単のため、 \( |z_1|=|z_2|=1 \) として、極形式を
$$ \begin{cases} z_1=\cos \theta_1+i\sin \theta_1 \\ z_2=\cos \theta_2+i\sin \theta_2 \end{cases} $$
とします。このとき、
$$ \begin{align} z_1z_2&=(\cos \theta_1+i\sin \theta_1)(\cos \theta_2+i\sin \theta_2) \\ &=(\cos \theta_1\cos \theta_2-\sin \theta_1\sin \theta_2)+i(\cos \theta_1\sin \theta_2+\sin \theta_1\cos \theta_2) \\ &=\cos(\theta_1+\theta_2)+i\sin (\theta_1+\theta_2) \end{align} $$
$$ \frac{z_1}{z_2}=\cos (\theta_1-\theta_2)+i\sin (\theta_1+\theta_2) $$
となるので、複素平面に図示すると次のようになります。
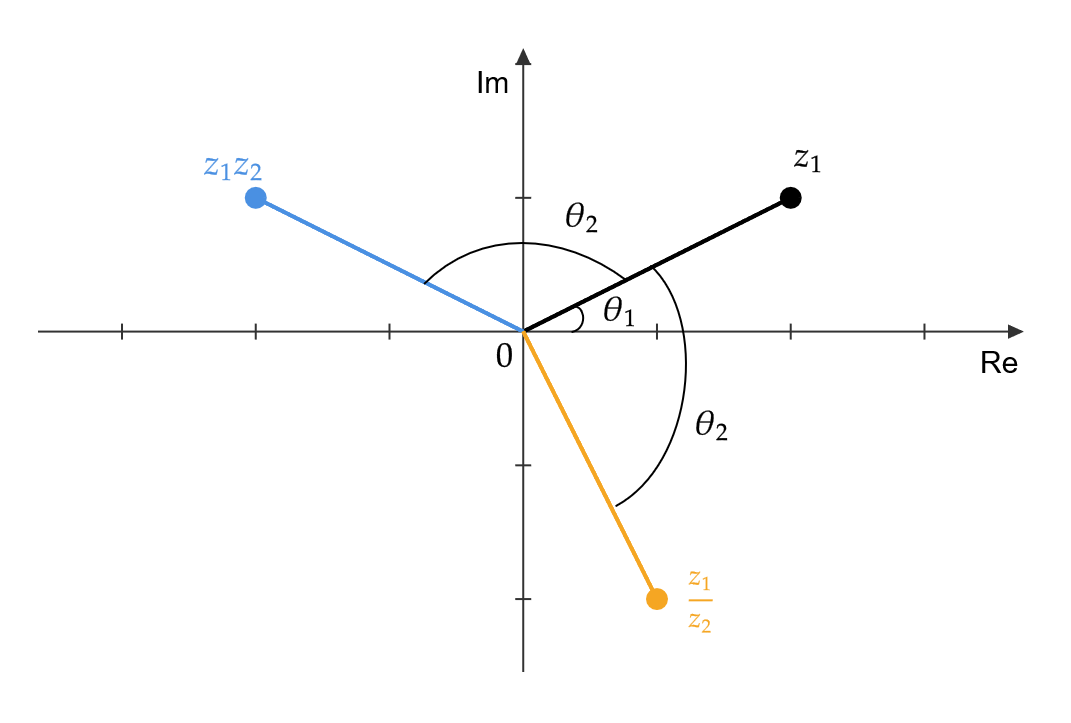
まとめると、
$$ z_1=r_1(\cos \theta_1+i\sin \theta_1), \ z_2=r_2(\cos \theta_2+i\sin \theta_2)\in \mathbb{C} $$
に対して、次が成り立つ。
(1) $$ \begin{cases} |z_1z_2|=|z_1||z_2| \\ \text{arg} \ (z_1z_2)=\text{arg} \ z_1+\text{arg} \ z_2 \end{cases} $$
つまり、
$$ z_1z_2=r_1r_2(\cos (\theta_1+\theta_2)+i\sin (\theta_1+\theta_2)) $$
(2) \( z_2\not=0 \) ならば、
$$ \begin{cases} |\frac{z_1}{z_2}|=\frac{|z_1|}{|z_2|} \\ \text{arg} \ \left(\frac{z_1}{z_2}\right)=\text{arg} \ z_1-\text{arg} \ z_2 \end{cases} $$
つまり、
$$ \frac{z_1}{z_2}=\frac{r_1}{r_2}(\cos (\theta_1-\theta_2)+i\sin (\theta_1-\theta_2)) $$
定理1より、次のド・モアブルの定理が成り立ちます。
$$ z=r(\cos \theta+i\sin \theta)\in \mathbb{C}, \quad n\in\mathbb{N} $$
に対して、次が成り立つ。
$$ z^n=(r(\cos \theta+i\sin \theta))^n=r^n(\cos (n\theta)+i\sin (n\theta)) $$
\( \theta\in\mathbb{R} \) に対して、
$$ (\cos \theta+i\sin \theta)^3=\cos^3\theta-3\cos\theta\sin^2\theta+i(3\cos^2\theta\sin \theta-\sin^3\theta) $$
となる。一方で、ド・モアブルの定理より、
$$ (\cos \theta+i\sin \theta)^3=\cos 3\theta+i\sin 3\theta $$
なので、これらを合わせることにより3倍角の公式
$$ \begin{cases} \cos 3\theta=\cos^3\theta-3\cos \theta\sin^2\theta \\ \sin 3\theta=3\cos^2\theta\sin\theta-\sin^3\theta \end{cases} $$
が成り立つ。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

