こんにちは、ひかりです。
今回は微分積分学から面積・体積と曲線・曲面積について解説していきます。
この記事では以下のことを紹介します。
- 図形の面積と回転体の体積について
- 曲線の長さについて
- 立体の体積と曲面の曲面積について
図形の面積と回転体の体積
まずはじめに、高校数学の復習として、図形の面積と回転体の体積を紹介します。
詳しくは、高校数学(数学Ⅲ)12および高校数学(数学Ⅲ)13の記事をご覧ください。
図形の面積
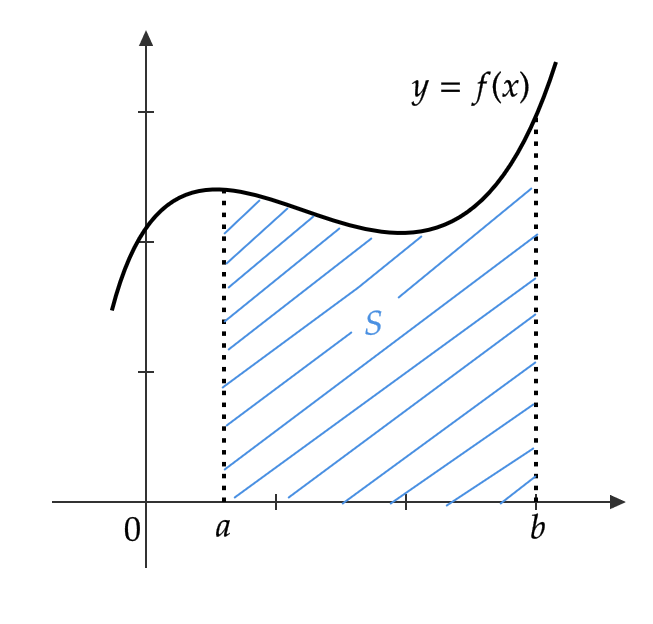
まず、 \( x \) 軸との図形の面積は次で与えられます。
区間 \( [a,b] \) において、 \( f(x)≧ 0 \) であるとき、曲線 \( y=f(x) \) と \( x \) 軸および \( x=a, \ x=b \) で囲まれた図形の面積 \( S \) は、次で与えられる。
$$ S=\int_a^bf(x)dx $$
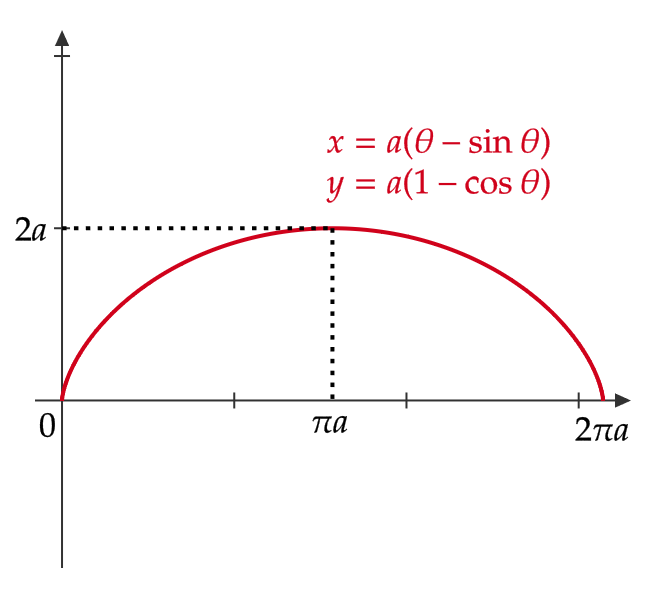
図のようなサイクロイド
$$ x=a(\theta-\sin \theta), \quad y=a(1-\cos\theta) $$
と \( x \) 軸で囲まれた図形の面積 \( S \) を求める。
ここで、 \( 0≦\theta≦2\pi, \ a>0 \)
$$ dx=a(1-\cos\theta)d\theta $$
より、
$$ \begin{align} S&=\int_0^{2\pi a}ydx=\int_0^{2\pi}a(1-\cos\theta)\cdot a(1-\cos\theta)d\theta \\ &=a^2\int_0^{2\pi}(1-\cos\theta)^2d\theta=a^2\int_0^{2\pi}(1-2\cos\theta+\cos^2\theta)d\theta \\ &=a^2\int_0^{2\pi}\left( \frac{3}{2}-2\cos \theta+\frac{1}{2}\cos 2\theta \right) d \theta \quad (倍角の公式より) \\ &=a^2 \left[ \frac{3}{2}\theta-2\sin \theta+\frac{1}{4} \sin 2\theta \right]^{2\pi}_0=3\pi a^2 \end{align} $$
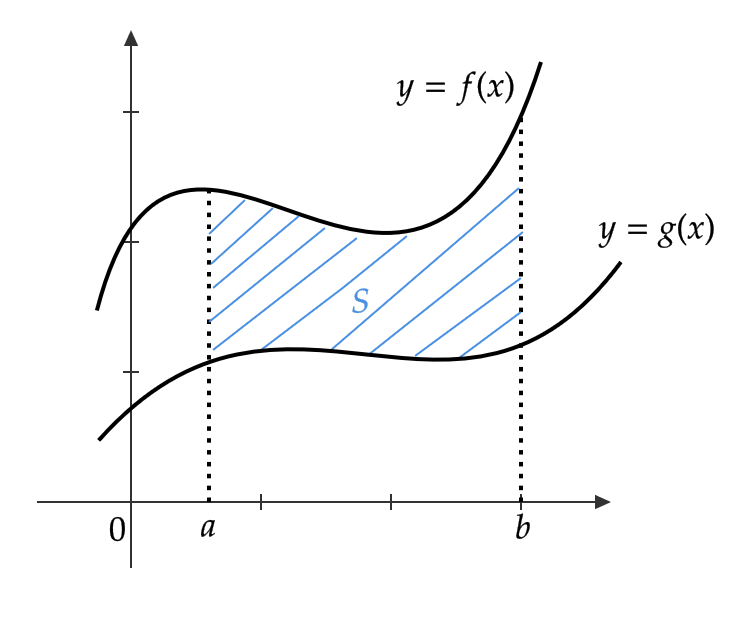
また、2曲線間の図形の面積は次で与えられます。
区間 \( a≦ x≦ b \) において、 \( f(x)≧ g(x) \) であるとき、 \( y=f(x), \ y=g(x), \ x=a, \ x=b \) で囲まれた図形の面積 \( S \) は、次で与えられる。
$$ S=\int_a^b\{ f(x)-g(x) \} dx $$
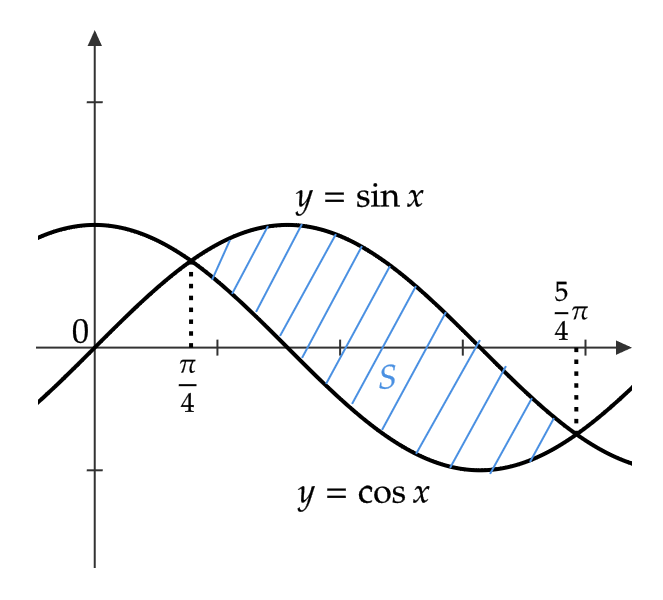
$$ y=\sin x, \ y=\cos x \left( \frac{\pi}{4}≦x≦\frac{5}{4}\pi \right) $$
で囲まれた図形の面積 \( S \) を求める。
$$ \begin{align} S&=\int_{\frac{\pi}{4}}^{\frac{5}{4}\pi}(\sin x-\cos x)dx=\left[ -\cos x-\sin x \right]^{\frac{5}{4}\pi}_{\frac{\pi}{4}} \\ &=-\left( \cos \frac{5}{4}\pi -\cos \frac{\pi}{4} \right)-\left( \sin \frac{5}{4}\pi-\sin \frac{\pi}{4} \right)=2\sqrt{2} \end{align} $$
回転体の体積
回転体の体積に関して、次が成り立ちます。
曲線 \( y=f(x) \) と \( x \) 軸および、 \( x=a, \ x=b \) で囲まれた図形を \( x \) 軸まわりに1回転したときの回転体の体積は次で与えられる。
$$ V=\pi\int_a^b\{ f(x)\}^2dx $$
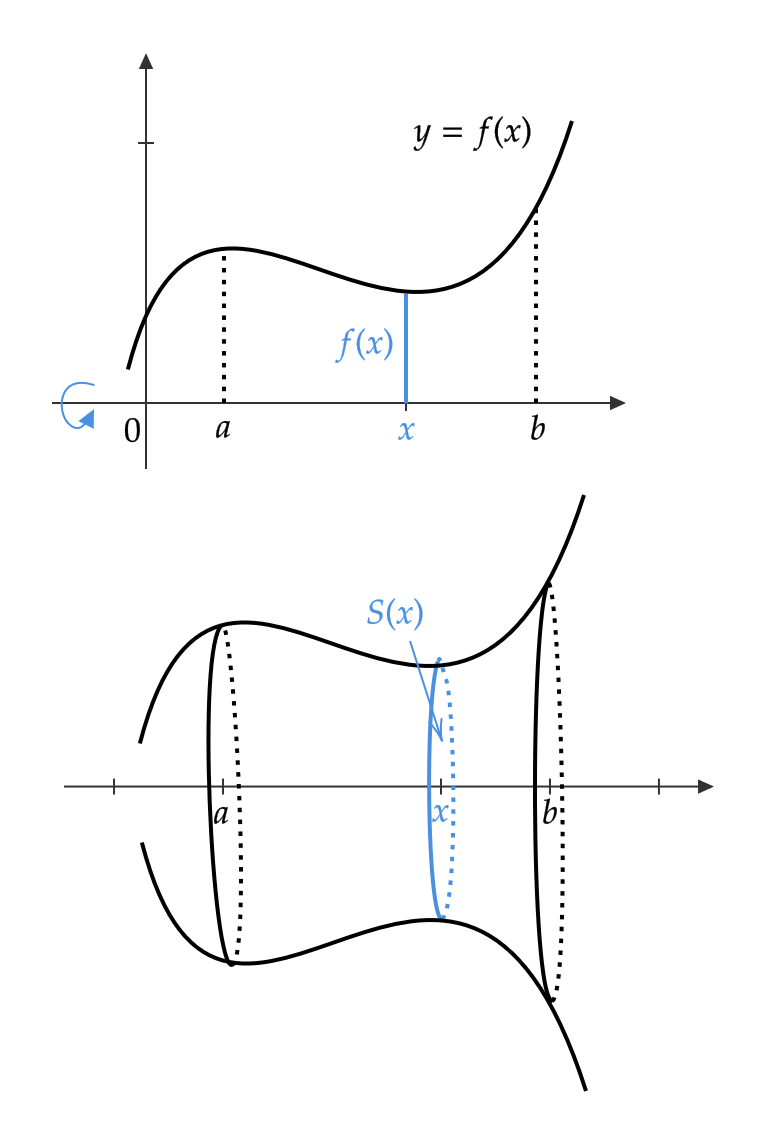
例1のサイクロイド
$$ x=a(\theta-\sin \theta), \quad y=a(1-\cos\theta) \quad (a>0, \ 0≦\theta≦2\pi) $$
を \( x \) 軸まわりに1回転したときの回転体の体積 \( V \) を求める。
$$ \begin{align} V&=\pi\int_0^{2\pi a}y^2dx=\pi a^3\int_0^{2\pi}(1-\cos \theta)^3d\theta \\ &=\pi a^3 \int_0^{2\pi}(1-3\cos \theta+3\cos^2\theta-\cos^3\theta)d\theta \\ &=\pi a^3\int_0^{2\pi}\left( \frac{5}{2}-\frac{15}{4}\cos \theta+\frac{3}{2}\cos 2\theta-\frac{1}{4}\cos 3\theta \right) d\theta \\ &=\pi a^3 \left[ \frac{5}{2}\theta-\frac{15}{4}\sin \theta+\frac{3}{4}\sin 2\theta-\frac{1}{12}\sin 3\theta \right]^{2\pi}_0=5\pi^2 a^3 \end{align} $$
曲線の長さ
今度は、2直線 \( x=a, \ x=b \) の区間における関数 \( y=f(x) \) により作られる曲線の長さ \( L \) を考えてみましょう。
関数 \( f(x) \) が閉区間 \( [a,b] \) 上で連続であるとする。
\( x \) 軸と平行な微小な幅 \( dx \) を考えて、
$$ f(x+dx)-f(x)=dy $$
とおきます。
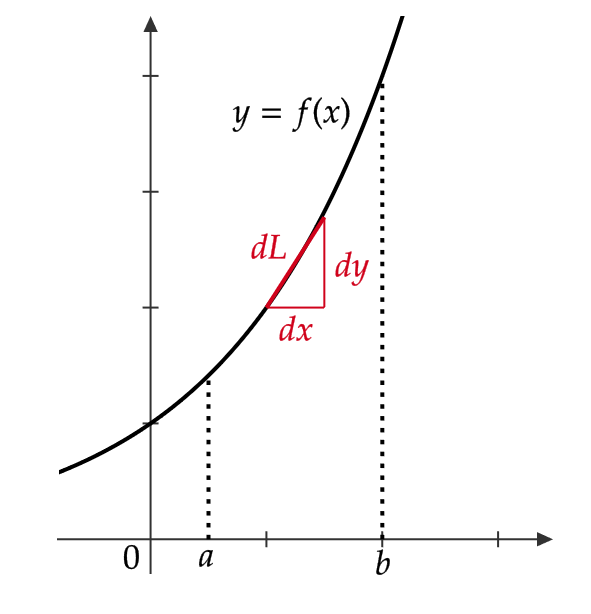
このとき、斜辺の長さ \( dL \) は次で与えられます。
$$ dL=\sqrt{(dx)^2+(dy)^2} $$
したがって、曲線の長さ \( L \) は区間 \( [a,b] \) で微小な斜辺の長さ \( dL \) を積分すれば得られます。
まとめると、
関数 \( y=f(x) \) が区間 \( [a,b] \) で連続かつ微分可能であるとする。
このとき、区間 \( [a,b] \) における曲線 \( y=f(x) \) の長さ \( L \) は次で与えられる。
$$ \begin{align} L&=\int_a^bdL=\int_a^b\sqrt{(dx)^2+(dy)^2} \\ &=\int_a^b\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx=\int_a^b\sqrt{1+(f'(x))^2}dx \end{align} $$
(1) 半径 \( r \) の円の周の長さ \( L \) を求める。
半径 \( r \) の円は \( x^2+y^2=r^2 \) で表されるので、
$$ y=\pm \sqrt{r^2-x^2} $$
よって、 \( x \) で微分すると、
$$ y’=\pm\frac{1}{2}(r^2-x^2)^{-\frac{1}{2}}(-2x)=\mp \frac{x}{\sqrt{r^2-x^2}} $$
よって、定理4より、
$$ \begin{align} L&=4\int_0^r\sqrt{1+(y’)^2}dx \quad (第 1 象限の部分の 4 倍でよい) \\ &=4\int_0^r\sqrt{1+\frac{x^2}{r^2-x^2}}dx=4r\int_0^r\frac{dx}{\sqrt{r^2-x^2}} \\ &=4r\lim_{\varepsilon\to+0}\int_0^{r-\varepsilon}\frac{dx}{\sqrt{r^2-x^2}} \quad (広義積分であることに注意) \\ &=4r\lim_{\varepsilon\to+0}\left[ \sin^{-1}\frac{x}{r} \right]^{r-\varepsilon}_0=4r\lim_{\varepsilon\to+0}\sin^{-1}\left( 1-\frac{\varepsilon}{r} \right)=2\pi r \end{align} $$
( \( \displaystyle \int\frac{dx}{\sqrt{r^2-x^2}} \) については、基本的な関数の積分の公式をご覧ください。)
よってこれは、半径 \( r \) の円の周の長さの公式と一致します。
(2) 例1のサイクロイド
$$ x=a(\theta-\sin \theta), \quad y=a(1-\cos\theta) \quad (a>0, \ 0≦\theta≦2\pi) $$
の周の長さ \( L \) を求める。
$$ dx=a(1-\cos \theta)d\theta, \quad dy=a\sin \theta d\theta $$
であるので、
$$ \begin{align} \sqrt{(dx)^2+(dy)^2}&=\sqrt{(a(1-\cos \theta)d \theta)^2+(a\sin \theta d \theta)^2} \\ &=\sqrt{a^2(1-\cos \theta)^2(d\theta)^2+a^2\sin^2\theta(d\theta)^2} \\ &=a\sqrt{2(1-\cos \theta)}d \theta=2a\sqrt{\sin^2 \left( \frac{\theta}{2} \right) }d\theta \\ &=2a\left| \sin \left( \frac{\theta}{2} \right) \right| d\theta=2a\sin \left( \frac{\theta}{2} \right) d\theta \quad (0≦\frac{\theta}{2}≦\pi より) \end{align} $$
定理4より、
$$ \begin{align} L&=\int_0^{2\pi a}\sqrt{(dx)^2+(dy)^2}=2a\int_0^{2\pi}\sin \left(\frac{\theta}{2} \right) d\theta \\ &=-4a\left[ \cos \left(\frac{\theta}{2}\right) \right]^{2\pi}_0=8a \end{align} $$
立体の体積と曲面の曲面積
立体の体積
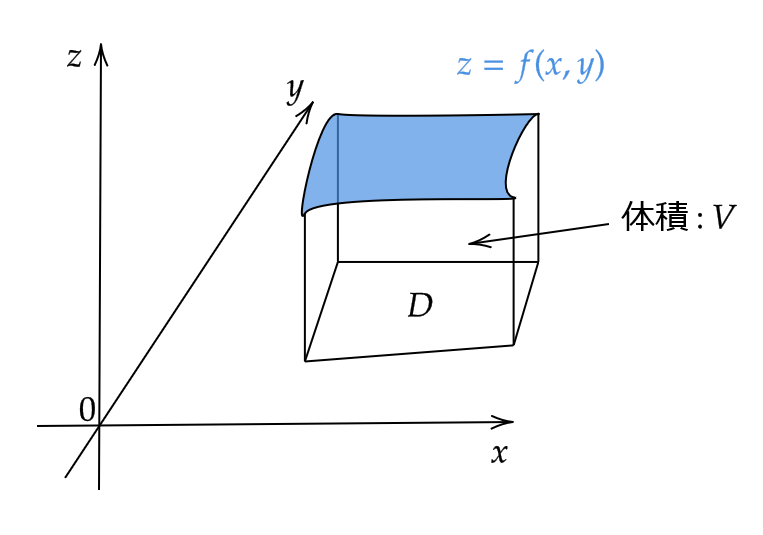
今度は、有界な集合 \( D \subset\mathbb{R}^2 \) 上の関数 \( z=f(x,y)≧0 \) を考えてみましょう。
このとき、集合
$$ \{ (x,y,z)|0≦z≦f(x,y), \ (x,y)\in D \} $$
の体積を \( V \) とおきます。(図をご覧ください。)
このとき、 \( D \) 上の微小面積 \( \Delta S_i \) を考えます。
このとき、その微小面積の集合内の点 \( (x_i,y_i) \) に対して、 \( f(x_i,y_i)\Delta S_i \) は底面積 \( \Delta S_i \) 、高さが \( f(x_i,y_i) \) の角柱の体積と考えることができます。
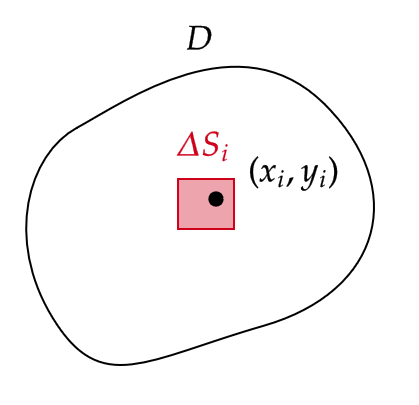
よって、リーマン和
$$ R_n=\sum_{i=1}^n f(x_i,y_i)\Delta S_i $$
は、体積 \( V \) を近似しています。つまり、
$$ V=\lim_{n\to \infty}\sum_{i=1}^n f(x_i,y_i)\Delta S_i $$
\( n\to \infty \) のとき、 \( \Delta S_i \to 0 \) となるので、積分の定義より、
$$ V=\iint_Df(x,y)dxdy $$
まとめると、
有界集合 \( D \) において、 \( f(x,y)≧0 \) であるとき、曲面 \( z=f(x,y) \) と \( z=0 \) ではさまれた集合
$$ \{ (x,y,z)|0≦z≦f(x,y), \ (x,y)\in D \} $$
の体積 \( V \) は、次で与えられる。
$$ V=\iint_Df(x,y)dxdy $$
$$ D=\{ (x,y) | x^2+y^2≦25, \ x,y≧0 \} $$
上で関数 \( f(x,y)=25-x^2-y^2 \) を考える。
このとき、曲面 \( z=f(x,y) \) と \( z=0 \) ではさまれた集合
$$ \{ (x,y,z)| 0≦z≦f(x,y), \ (x,y)\in D \} $$
の体積 \( V \) を求める。極座標変換
$$ x=r\cos \theta, \quad y=r\sin \theta $$
により、 \( D \) は次のように書き換えられる。
$$ \left\{ (r,\theta) | 0≦r≦5, \ 0≦\theta≦\frac{\pi}{2} \right\} $$
よって、 \( J(r,\theta)=r \) より、
$$ \begin{align} V&=\iint_Df(x,y)dxdy=\int_0^5\int_0^{\frac{\pi}{2}}(25-r^2)\cdot rd\theta dr \\ &=\left( \int_0^5(25r-r^3)dr\right)\left( \int_0^{\frac{\pi}{2}}d\theta \right) \\ &=\left[ \frac{25}{2}r^2-\frac{r^4}{4} \right]^5_0\left[ \theta \right]^{\frac{\pi}{2}}_0=\frac{625}{8}\pi \end{align} $$
面積のときと同様に、2曲面にはさまれた集合の体積も次で与えられます。
有界集合 \( D \) において、 \( f(x,y)≧g(x,y) \) であるとき、2曲面 \( z=f(x,y) \) と \( z=g(x,y) \) ではさまれた集合
$$ \{ (x,y,z)|g(x,y)≦z≦f(x,y), \ (x,y)\in D \} $$
の体積 \( V \) は、次で与えられる。
$$ V=\iint_D\{f(x,y)-g(x,y) \}dxdy $$
曲面の曲面積
最後に、集合 \( D \) 上の \( C^1 \) 級の曲面 \( z=f(x,y) \) の曲面積 \( S \) を求めることを考えてみましょう。
まず、 \( D \) 内に微小な長方形
$$ \Delta R=\{ (x,y) | x_0≦x≦x_0+\Delta x, \ y_0≦y≦y_0+\Delta y \} $$
を考えます。(図をご覧ください。)
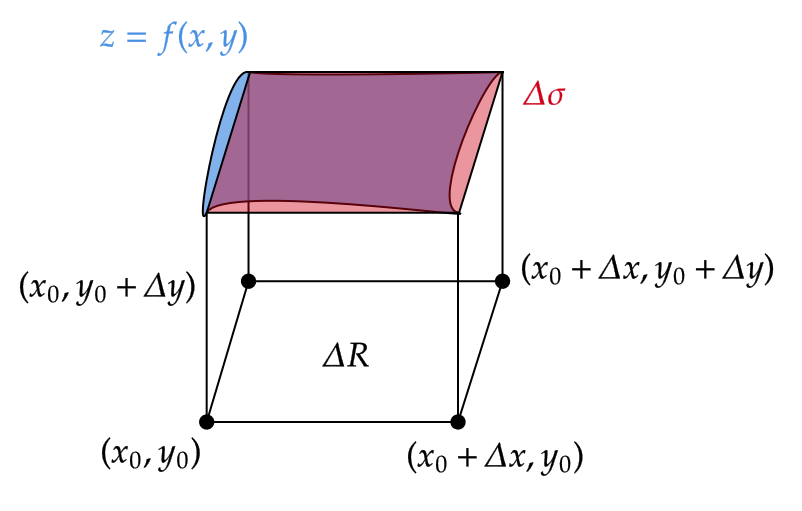
このとき、各頂点
$$ (x_0,y_0), \ (x_0+\Delta x,y_0), \ (x_0,y_0+\Delta y_0), \ (x_0+\Delta x,y_0+\Delta y) $$
に対応する関数 \( f(x,y) \) の点
$$ Q_0=(x_0,y_0,f(x_0,y_0)), \ Q_1=(x_0+\Delta x,y_0,f(x_0+\Delta x,y_0)), $$
$$ Q_2=(x_0,y_0+\Delta y,f(x_0,y_0+\Delta y_0)), \ Q_3=(x_0+\Delta x,y_0+\Delta y,f(x_0+\Delta x,y_0+\Delta y)) $$
からなる平行四辺形 \( \Delta \sigma \) はもともとの曲線を近似しています。
ここで、
$$ |\overrightarrow{Q_0Q_1}|^2=(\Delta x)^2+(f(x_0+\Delta x,y_0)-f(x_0,y_0))^2 $$
$$ |\overrightarrow{Q_0Q_2}|^2=(\Delta y)^2+(f(x_0,y_0+\Delta y)-f(x_0,y_0))^2 $$
$$ \begin{align} \overrightarrow{Q_0Q_1}\cdot \overrightarrow{Q_0Q_2}&=(\Delta x,0,f(x_0+\Delta x,y_0)-f(x_0,y_0))\cdot (0,\Delta y,f(x_0,y_0+\Delta y)-f(x_0,y_0)) \\ &=(f(x_0+\Delta x,y_0)-f(x_0,y_0))(f(x_0,y_0+\Delta y)-f(x_0,y_0)) \end{align} $$
であり、 \( \Delta \sigma \) が平行四辺形であることに注意すると、
$$ \begin{align} (\Delta \sigma)^2&=|\overrightarrow{Q_0Q_1}|^2|\overrightarrow{Q_0Q_2}|^2-(\overrightarrow{Q_0Q_1}\cdot \overrightarrow{Q_0Q_2})^2 \\ &=(\Delta x\Delta y)^2+\{ \Delta y(f(x_0+\Delta x,y_0)-f(x_0,y_0))\}^2 \\ & \quad +\{ \Delta x(f(x_0,y_0+\Delta y)-f(x_0,y_0)) \}^2 \\ &=(\Delta x\Delta y)^2\left\{ 1+\left( \frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x} \right)^2\right. \\ & \quad \left. +\left( \frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}\right)^2\right\} \tag{1} \end{align} $$
ここで、
$$ \lim_{\Delta x\to0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=f_x $$
$$ \lim_{\Delta y \to0}\frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}=f_y $$
より、式(1)を \( \Delta x \to 0, \ \Delta y\to0 \) とすると、
$$ d\sigma=\sqrt{1+(f_x)^2+(f_y)^2}dxdy $$
よって、曲面積 \( S \) はこの \( d\sigma \) を集合 \( D \) 上で積分すれば求まります。つまり、
$$ S=\iint_Dd\sigma=\iint_D\sqrt{1+(f_x)^2+(f_y)^2}dxdy $$
まとめると、
関数 \( f(x,y) \) が集合 \( D \) で \( C^1 \) 級であるとする。
このとき、 \( D \) における曲面 \( z=f(x,y) \) の曲面積 \( S \) は次で与えられる。
$$ S=\iint_Dd\sigma=\iint_D\sqrt{1+(f_x)^2+(f_y)^2}dxdy $$
半径 \( r \) の球の表面積 \( S \) を求める。
半径 \( r \) の球は \( x^2+y^2+z^2=r^2 \) で表されるので、
$$ z=\pm \sqrt{r^2-x^2-y^2} $$
よって、 \( x, \ y \) で偏微分すると、
$$ z_x=\pm\frac{1}{2}(r^2-x^2-y^2)^{-\frac{1}{2}}(-2x)=\mp \frac{x}{\sqrt{r^2-x^2-y^2}} $$
$$ z_y=\pm\frac{1}{2}(r^2-x^2-y^2)^{-\frac{1}{2}}(-2y)=\mp \frac{y}{\sqrt{r^2-x^2-y^2}} $$
よって、定理7より、
$$ \begin{align} S&=8\int_0^r\int_0^{\sqrt{r^2-x^2}}\sqrt{1+(z_x)^2+(z_y)^2}dydx \quad (x,y,z≧0の部分の 8 倍でよい) \\ &=8\int_0^r\int_0^{\sqrt{r^2-x^2}}\sqrt{1+\frac{x^2}{r^2-x^2-y^2}+\frac{y^2}{r^2-x^2-y^2}}dydx \\ &=8r\int_0^r\int_0^{\sqrt{r^2-x^2}}\frac{dydx}{\sqrt{r^2-x^2-y^2}} \\ &=8r\int_0^r\lim_{\varepsilon\to+0}\int_0^{\sqrt{r^2-x^2}-\varepsilon}\frac{dy}{\sqrt{r^2-x^2-y^2}}dx \quad (広義積分であることに注意) \\ &=8r\int_0^r\lim_{\varepsilon\to+0}\left[ \sin^{-1}\frac{y}{\sqrt{r^2-x^2}} \right]^{\sqrt{r^2-x^2}-\varepsilon}_0dx \\ &=8r\int_0^r\lim_{\varepsilon\to+0}\sin^{-1}\left( 1-\frac{\varepsilon}{\sqrt{r^2-x^2}} \right)dx=4\pi r\int_0^rdx=4\pi r^2 \end{align} $$
( \( \displaystyle \int\frac{dy}{\sqrt{r^2-x^2-y^2}} \) については、基本的な関数の積分の公式をご覧ください。)
よってこれは、半径 \( r \) の球の表面積の公式と一致します。
今回までで微分積分学の内容について特に重要性の高いところを一通り紹介しました。お疲れ様でした。
次に勉強するのにおすすめなシリーズとしては、「線形代数学」シリーズもしくは「確率・統計」シリーズとなっています。
それでは、またどこかの記事でお会いしましょう。ひかりでした。

