こんにちは、ひかりです。
今回は微分積分学から多変数関数の積分の変数変換について解説していきます。
この記事では以下のことを紹介します。
- 2重積分の変数変換について
- 極座標変換について
- よく用いられる3変数関数の変数変換について
2重積分の変数変換
まず、1変数関数の積分の変数変換について復習してみましょう。
置換積分の公式より、次にようになります。
$$ \int_a^bf(x)dx=\int_{\alpha}^{\beta}f(\varphi(t))\varphi'(t)dt \quad (a=\varphi(\alpha), \ b=\varphi(\beta)) $$
\( a<b \) とします。このとき、 \( \varphi \) が増加するか減少するかにより、 \( \alpha<\beta \) または \( \beta<\alpha \) となります。
どちらであったとしても、 \( I \) を \( \alpha,\beta \) を両端にもつ閉区間とすると、 \( [a,b]=\varphi(I) \) より、次が成り立ちます。
$$ \int_{\varphi(I)}f(x)dx=\int_If(\varphi(t))|\varphi'(t)|dt \tag{1} $$
( \( \alpha<\beta \) のとき \( \varphi'(t)>0 \) であり、 \( \beta<\alpha \) のとき \( \varphi'(t)<0 \) となることに注意しましょう)
この変数変換の公式を2重積分に対しても考えてみましょう。
そのために、次を定義します。
変数変換
$$ T \ : \ \begin{pmatrix} s \\ t \end{pmatrix} \mapsto \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} \phi(s,t) \\ \psi(s,t) \end{pmatrix} $$
に対して、 \( \phi, \ \psi \) が \( C^1 \) 級であるとき、
$$ \det \begin{pmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \end{pmatrix}=\det \begin{pmatrix} \frac{\partial \phi}{\partial s}(s,t) & \frac{\partial \phi}{\partial t}(s,t) \\ \frac{\partial \psi}{\partial s}(s,t) & \frac{\partial \psi}{\partial t}(s,t) \end{pmatrix} $$
を \( T \) のヤコビアンといい、 \( J(s,t) \) もしくは \( \frac{\partial (x,y)}{\partial (s,t)} \) と書く。ここで、
$$ \det \begin{pmatrix} a & b \\ c & d \end{pmatrix}=ad-bc $$
(1) (一次変換)
\( T \) を一次変換、すなわち、
$$ T:\begin{pmatrix} s \\ t \end{pmatrix} \mapsto \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} s \\ t \end{pmatrix} $$
とする。このとき、
$$ \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} s \\ t \end{pmatrix}=\begin{pmatrix} as+bt \\ cs+dt \end{pmatrix} $$
より、
$$ J(s,t)=\det \begin{pmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \end{pmatrix}=\det \begin{pmatrix} a & b \\ c & d \end{pmatrix}=ad-bc $$
(2) (回転)
\( T \) を点の原点まわりの回転移動、すなわち、
$$ T:\begin{pmatrix} s \\ t \end{pmatrix} \mapsto \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}\begin{pmatrix} s \\ t \end{pmatrix} $$
とする。このとき、
$$ \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}\begin{pmatrix} s \\ t \end{pmatrix}=\begin{pmatrix} s\cos \theta-t\sin \theta \\ s\sin \theta+t\cos \theta \end{pmatrix} $$
より、
$$ J(s,t)=\det \begin{pmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \end{pmatrix}=\det \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}=\cos^2\theta+\sin^2\theta=1 $$
(3) (平行移動)
\( T \) を平行移動、すなわち、
$$ T:\begin{pmatrix} s \\ t \end{pmatrix} \mapsto \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} s+a \\ t+b \end{pmatrix} $$
とする。ここで、 \( a,b \) は定数である。このとき、
$$ J(s,t)=\det \begin{pmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \end{pmatrix}=\det \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}=1 $$
また、関数の全単射についても定義します。(詳しいことは線形代数学続論01の記事をご覧ください)
2つの集合 \( X, \ Y \) に対して、 \( X \) から \( Y \) への関数を \( f \) とする。
(1) \( f \) の値域を \( f(X) \) と表す。 \( Y=f(X) \) であるとき、 \( f \) は全射であるという。
(2) \( x_1,x_2 \in X \) に対して、
$$ f(x_1)=f(x_2) \quad ならば \quad x_1=x_2 $$
が成り立つとき、 \( f \) は単射であるという。
(3) \( f \) が全射かつ単射であるとき、全単射であるという。
これを用いると、次の変数変換の公式が成り立ちます。
全単射な変数変換
$$ T \ : \ \begin{pmatrix} s \\ t \end{pmatrix} \mapsto \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} \phi(s,t) \\ \psi(s,t) \end{pmatrix} $$
によって、 \( st \) 平面上の集合 \( \Omega \) が \( xy \) 平面上の集合 \( D \) に写されるとする。
また、 \( \phi, \ \psi \) は \( \Omega \) 上で \( C^1 \) 級で \( J(s,t)\not=0 \) であるとする。
このとき、 \( \overline{D} \) ( \( D \) の閉包)上で連続な関数 \( f \) に対して、次が成り立つ。
$$ \iint_Df(x,y)dxdy=\iint_{\Omega}f(\phi(s,t),\psi(s,t))|J(s,t)|dsdt $$
定理1の証明(気になる方だけクリックしてください)
ここでは、定理1の証明の概略だけを述べます。詳細はここでは省略します。
2変数関数の平均値の定理より、点 \( (s_0,t_0) \) のまわりで、
$$ \begin{align} x&=\phi(s,t) \\ &=\phi(s_0,t_0)+\phi_s(s_1,t_1)(s-s_0)+\phi_t(s_1,t_1)(t-t_0) \end{align} $$
$$ \begin{align} y&=\psi(s,t) \\ &=\psi(s_0,t_0)+\psi_s(s_2,t_2)(s-s_0)+\psi_t(s_2,t_2)(t-t_0) \end{align} $$
をみたす \( s_1,s_2 \) が \( s_0 \) と \( s \) の間に、 \( t_1,t_2 \) が \( t \) と \( t_0 \) の間に存在します。
よって、
$$ \begin{pmatrix} s_0 \\ t_0 \end{pmatrix} \mapsto \begin{pmatrix} x_0 \\ y_0 \end{pmatrix}=\begin{pmatrix} \phi(s_0,t_0) \\ \psi(s_0,t_0) \end{pmatrix} $$
に十分近いところでは、
$$ \begin{align} \begin{pmatrix} x \\ y \end{pmatrix}&=\begin{pmatrix} x_0-\phi_s(s_0,t_0)s_0-\phi_t(s_0,t_0)t_0 \\ y_0-\psi_s(s_0,t_0)s_0-\psi_t(s_0,t_0)t_0 \end{pmatrix} \\ & \quad +\begin{pmatrix} \phi_s(s_0,t_0) & \phi_t(s_0,t_0) \\ \psi_s(s_0,t_0) & \psi_t(s_0,t_0) \end{pmatrix}\begin{pmatrix} s \\ t \end{pmatrix} \end{align} $$
と近似することができます。
これは、例1の(1),(3)で紹介した平行移動と一次変換の合成となっています。
ここで、 \( xy \) 平面での図形を平行移動と一次変換で \( st \) 平面に写したときの図形の面積の比を考えると、 \( |J(s_0,t_0)| \) で近似することができます。
これはつまり、
$$ dxdy=|J(s,t)|dsdt $$
(1) $$ D=\{ (x,y)|-1≦x-y≦1, \ -1≦x+y≦1 \} $$
のとき、次の積分を求める。
$$ \iint_D(x-y)^2(x+y)^4 dxdy $$
\( s=x-y, \ t=x+y \) と変数変換をおこなう。すると、 \( D \) の範囲は
$$ -1≦s≦1, \quad -1≦t≦1 $$
ヤコビアンを求める。
$$ x=\frac{s+t}{2}, \ y=\frac{-s+t}{2} $$
より、
$$ J(s,t)=\det \begin{pmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \end{pmatrix}=\det \begin{pmatrix} \frac{1}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} \end{pmatrix}=\frac{1}{2} $$
よって、定理1により、積分の変数変換をすると、
$$ \begin{align} &\iint_D(x-y)^2(x+y)^4 dxdy=\int_{-1}^1\int_{-1}^1s^2t^4|J(s,t)|dtds \\ &=\frac{1}{2}\left( \int_{-1}^1 s^2 ds \right)\left( \int_{-1}^1 t^4 dt \right)=\frac{1}{2}\left[\frac{1}{3}s^3\right]^1_{-1}\left[ \frac{1}{5}t^5 \right]^1_{-1}=\frac{2}{15} \end{align} $$
(2) $$ D=\{ (x,y)|0≦2x+3y≦1, \ -1≦3x+5y≦1 \} $$
のとき、次の積分を求める。
$$ \iint_D(2x+3y)e^xdxdy $$
\( s=2x+3y, \ t=3x+5y \) と変数変換をおこなう。すると、 \( D \) の範囲は
$$ 0≦s≦1, \quad -1≦t≦1 $$
ヤコビアンを求める。
$$ x=5s-3t, \ y=-3s+2t $$
より、
$$ J(s,t)=\det \begin{pmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} \end{pmatrix}=\det \begin{pmatrix} 5 & -3 \\ -3 & 2 \end{pmatrix}=1 $$
よって、定理1により、積分の変数変換をすると、
$$ \begin{align} &\iint_D(2x+3y)e^xdxdy=\int_0^1\int_{-1}^1se^{5s-3t}|J(s,t)|dtds \\ &=\left( \int_0^1 se^{5s} ds \right)\left( \int_{-1}^1 e^{-3t} dt \right) \\ &=\left\{\left[\frac{1}{5}se^{5s} \right]^1_0-\frac{1}{5}\int_0^1e^{5s}ds \right\}\left[ -\frac{1}{3}e^{-3t} \right]^1_{-1} \\ &=\left[\frac{1}{5}se^{5s}-\frac{1}{25}e^{5s}\right]^1_0\left[ -\frac{1}{3}e^{-3t} \right]^1_{-1} \\ &=\left\{ \left( \frac{1}{5}e^5-\frac{1}{25}e^5 \right)-\left( -\frac{1}{25} \right) \right\}\left( -\frac{1}{3}e^{-3}+\frac{1}{3}e^3 \right) \\ &=\left( \frac{4}{25}e^5+\frac{1}{25} \right)\left( \frac{1}{3}e^3-\frac{1}{3}e^{-3} \right) \end{align} $$
極座標変換
2変数関数の積分の変数変換でよく用いられているものとして、極座標変換があります。
極座標変換
$$ T:\begin{pmatrix} r \\ \theta \end{pmatrix} \mapsto \begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} r\cos \theta \\ r\sin\theta \end{pmatrix} $$
を考える。ここで、 \( r≧0, \ 0≦\theta<2\pi \) である。このとき、
$$ \begin{align} J(r,\theta)&=\det \begin{pmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{pmatrix}=\det \begin{pmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \end{pmatrix} \\ &=r\cos^2\theta+r\sin^2\theta=r \end{align} $$
よって、
$$ dxdy=rdrd\theta $$
と積分の変数変換がされる。
これを用いて積分を計算してみましょう。
(1) $$ D=\left\{ (x,y)| \ x^2+y^2≦1 \right\} $$
のとき、次の積分を求める。
$$ \iint_Dx^2dxdy $$
\( x=r\cos\theta, \ y=r\sin\theta \) と変数変換をおこなう。すると、
$$ \begin{align} x^2+y^2&=r^2\cos^2\theta+r^2\sin^2\theta=r^2 \end{align} $$
であるので、 \( D \) の範囲は \( r^2≦1 \) となる。つまり、
$$ 0≦r≦1, \ 0≦\theta≦2\pi $$
また、例3よりヤコビアンは \( J(r,\theta)=r \)
よって、定理1により、積分の変数変換をすると、2倍角の公式を駆使することにより、
$$ \begin{align} \iint_Dx^2dxdy&=\int_0^{2\pi}\int_0^1r^2\cos^2\theta\cdot rdrd\theta \\ &=\left(\int_0^{2\pi}\cos^2\theta d\theta \right) \left( \int_0^1 r^3dr \right) \\ &=\int_0^{2\pi}\frac{1+\cos 2\theta}{2}d\theta\left[ \frac{1}{4}r^4 \right]^1_0 \\ &=\frac{1}{4}\left[ \frac{1}{2}\cdot \theta+\frac{1}{2}\cdot \frac{1}{2}\sin 2\theta \right]^{2\pi}_0=\frac{\pi}{4} \end{align} $$
(2) $$ D=\left\{ (x,y)| \ \frac{x^2}{a^2}+\frac{y^2}{b^2}≦1 (a>0,b>0), \ x≧0, \ y≧0 \right\} $$
のとき、次の積分を求める。
$$ \iint_D(x^2+y^2)dxdy $$
\( x=ar\cos\theta, \ y=br\sin\theta \) と変数変換をおこなう。すると、
$$ \begin{align} \frac{x^2}{a^2}+\frac{y^2}{b^2}&=\frac{a^2r^2\cos^2\theta}{a^2}+\frac{b^2r^2\sin^2\theta}{b^2} \\ &=r^2\cos^2\theta+r^2\sin^2\theta=r^2 \end{align} $$
であるので、 \( D \) の範囲は
$$ r^2≦1, \ r\cos\theta≧0, \ r\sin\theta≧0 $$
つまり、
$$ 0≦r≦1, \ 0≦\theta≦\frac{\pi}{2} $$
ヤコビアンを求める。
$$ \begin{align} J(r,\theta)&=\det \begin{pmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{pmatrix}=\det \begin{pmatrix} a\cos\theta & -ar\sin\theta \\ b\sin\theta & br\cos\theta \end{pmatrix} \\ &=(a\cos\theta)(br\cos\theta)-(-ar\sin\theta)(b\sin\theta) \\ &=abr(\cos^2\theta+\sin^2\theta)=abr \end{align} $$
よって、定理1により、積分の変数変換をすると、2倍角の公式を駆使することにより、
$$ \begin{align} &\iint_D(x^2+y^2)dxdy=\int_0^{\frac{\pi}{2}}\int_0^1(a^2r^2\cos^2\theta+b^2r^2\sin^2\theta)|J(r,\theta)|drd\theta \\ &=ab\left( \int_0^{\frac{\pi}{2}}a^2\cos^2\theta+b^2\sin^2\theta d\theta\right)\left( \int_0^1r^3dr \right) \\ &=ab\left( \int_0^{\frac{\pi}{2}}a^2\cdot \frac{1+\cos 2\theta}{2}+b^2\cdot \frac{1-\cos 2\theta}{2}d\theta \right) \left[ \frac{1}{4}r^4 \right]^1_0 \\ &=\frac{ab}{4} \left[ \frac{a^2+b^2}{2}\cdot \theta+\frac{a^2-b^2}{2}\cdot \frac{1}{2}\sin 2\theta \right]^{\frac{\pi}{2}}_0=\frac{ab(a^2+b^2)\pi}{16} \end{align} $$
よく用いられる3変数関数の変数変換
3変数関数にも有名な変数変換があるためここで紹介しておきます。
2変数関数のときは長方形 \( R_{ij} \) で分割をしたリーマン和を考えることによって、2重積分が定義されました。
同様に、3変数関数のときは直方体で分割をしたリーマン和を考えることにより、3重積分が定義されます。
\( xyz \) 空間上の集合 \( V \) 上での関数 \( f(x,y,z) \) の3重積分を次のように表します。
$$ \iiint_Vf(x,y,z)dxdydz $$
変数変換の公式も2変数関数同様に成り立ちますが、その際のヤコビアンは次のようになることに注意してください。
$$ \begin{align} J(s,t,u)&=\det \begin{pmatrix} \frac{\partial x}{\partial s} & \frac{\partial x}{\partial t} & \frac{\partial x}{\partial u} \\ \frac{\partial y}{\partial s} & \frac{\partial y}{\partial t} & \frac{\partial y}{\partial u} \\ \frac{\partial z}{\partial s} & \frac{\partial z}{\partial t} & \frac{\partial z}{\partial u} \end{pmatrix} \end{align} $$
では、3変数関数の有名な変数変換である円柱座標変換と球座標変換について紹介します。
(1) (円柱座標変換)
$$ T:\begin{pmatrix} r \\ \theta \\ z \end{pmatrix} \mapsto \begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} r\cos \theta \\ r\sin\theta \\ z \end{pmatrix} $$
を考える。ここで、 \( r≧0, \ 0≦\theta<2\pi, \) である。このとき、
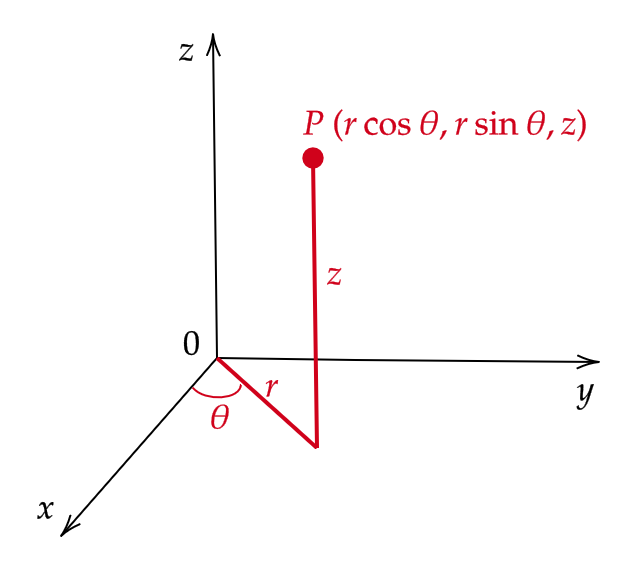
$$ \begin{align} J(r,\theta,z)&=\det \begin{pmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z} \end{pmatrix}=\det \begin{pmatrix} \cos\theta & -r\sin\theta & 0 \\ \sin\theta & r\cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} \\ &=r\cos^2\theta+r\sin^2\theta=r \end{align} $$
(3次正方行列の行列式の求め方については線形代数学07の記事をご覧ください。)
よって、
$$ dxdydz=rdrd\theta dz $$
と積分の変数変換がされる。
(2) (球座標変換もしくは空間での極座標変換)
$$ T:\begin{pmatrix} r \\ \theta \\ \varphi \end{pmatrix} \mapsto \begin{pmatrix} x \\ y \\ z \end{pmatrix}=\begin{pmatrix} r\sin \theta\cos\varphi \\ r\sin\theta\sin\varphi \\ r\cos \theta \end{pmatrix} $$
を考える。ここで、 \( r≧0, \ 0≦\theta≦\pi, \ 0≦\varphi≦2\pi \) である。このとき、
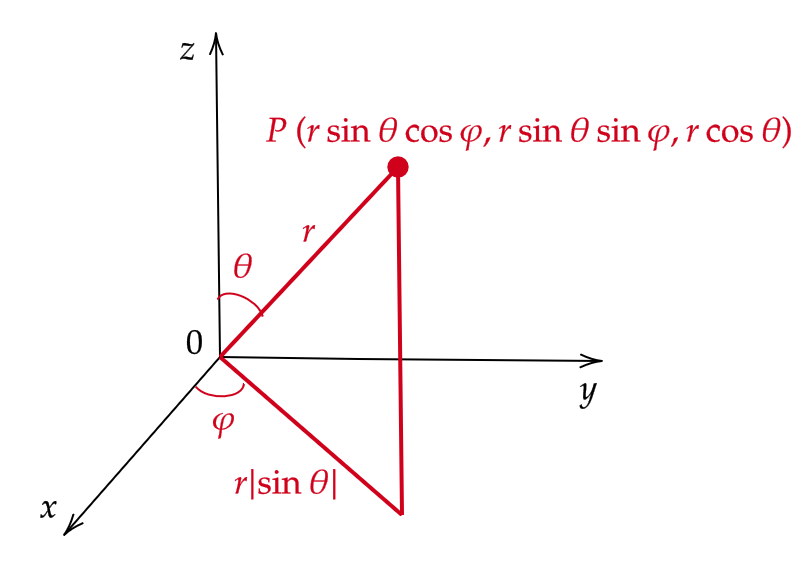
$$ \begin{align} J(r,\theta,\varphi)&=\det \begin{pmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \varphi} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \varphi} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \varphi} \end{pmatrix}=\det \begin{pmatrix} \sin\theta\cos\varphi & r\cos\theta\cos\varphi & -r\sin\theta\sin\varphi \\ \sin\theta\sin\varphi & r\cos\theta\sin\varphi & r\sin\theta\cos\varphi \\ \cos\theta & -r\sin\theta & 0 \end{pmatrix} \\ &=r^2(\cos^2\theta\sin\theta\cos^2\varphi+\sin^3\theta\sin^2\varphi+\sin^3\theta\cos^2\varphi+\sin\theta\cos^2\theta\sin^2\varphi) \\ &=r^2\sin\theta \end{align} $$
(3次正方行列の行列式の求め方については線形代数学07の記事をご覧ください。)
よって、
$$ dxdydz=r^2\sin\theta drd\theta d\varphi $$
と積分の変数変換がされる。
これを用いて積分を計算してみましょう。
(1) $$ V=\left\{ (x,y,z)| \ x^2+y^2+|z|≦1 \right\} $$
のとき、次の積分を求める。
$$ \iiint_Vx^2dxdydz $$
\( x=r\cos\theta, \ y=r\sin\theta, \ z=z \) と変数変換をおこなう。すると、
$$ \begin{align} x^2+y^2+|z|&=r^2\cos^2\theta+r^2\sin^2\theta+|z|=r^2+|z| \end{align} $$
であるので、 \( V \) の範囲は \( r^2+|z|≦1 \) となる。つまり、
$$ 0≦r≦1, \ 0≦\theta≦2\pi, \ 0≦|z|≦1-r^2 $$
また、例5(1)よりヤコビアンは \( J(r,\theta,z)=r \)
よって、
$$ \int_{0≦|z|≦1-r^2}dz=\int_0^{1-r^2}dz+\int_{r^2-1}^0dz=2\int_0^{1-r^2}dz $$
に注意して、積分の変数変換をすると、2倍角の公式を駆使することにより、
$$ \begin{align} \iiint_Vx^2dxdydz&=\int_0^{2\pi}\int_0^1\int_{0≦|z|≦1-r^2}r^2\cos^2\theta\cdot rdzdrd\theta \\ &=\left(\int_0^{2\pi}\cos^2\theta d\theta \right) \left( \int_0^1 r^3\left( \int_{0≦|z|≦1-r^2}dz \right)dr \right) \\ &=2\left(\int_0^{2\pi}\frac{1+\cos 2\theta}{2}d\theta\right) \left( \int_0^1 r^3\left( \int_0^{1-r^2}dz \right)dr \right) \\ &=2\left[ \frac{1}{2}\cdot \theta+\frac{1}{2}\cdot \frac{1}{2}\sin 2\theta \right]^{2\pi}_0\left( \int_0^1 r^3\left[ z \right]^{1-r^2}_0dr \right) \\ &=2\pi\int_0^1 r^3(1-r^2)dr=2\pi\left[\frac{1}{4}r^4-\frac{1}{6}r^6 \right]^1_0=\frac{\pi}{6} \end{align} $$
(2) $$ V=\left\{ (x,y,z)| \ x^2+y^2+z^2≦1 \right\} $$
のとき、次の積分を求める。
$$ \iiint_Vx^2dxdydz $$
球座標変換
$$ x=r\sin\theta\cos\varphi, \quad y=r\sin\theta\sin\varphi, \quad z=r\cos\theta $$
をおこなう。すると、
$$ \begin{align} x^2+y^2+z^2&=r^2\sin^2\theta\cos^2\varphi+r^2\sin^2\theta\sin^2\varphi+r^2\cos^2\theta \\ &=r^2\sin^2\theta(\cos^2\varphi+\sin^2\varphi)+r^2\cos^2\theta \\ &=r^2(\sin^2\theta+\cos^2\theta)=r^2 \end{align} $$
であるので、 \( V \) の範囲は \( r^2≦1 \) となる。つまり、
$$ 0≦r≦1, \ 0≦\theta≦\pi, \ 0≦\varphi≦2\pi $$
また、例5(2)よりヤコビアンは \( J(r,\theta,\varphi)=r^2\sin\theta \)
よって、積分の変数変換をすると、2倍角と3倍角の公式を駆使することにより、
$$ \begin{align} \iiint_Vx^2dxdydz&=\int_0^{2\pi}\int_0^{\pi}\int_0^1r^2\sin^2\theta\cos^2\varphi\cdot r^2\sin\theta drd\theta d\varphi \\ &=\left( \int_0^{2\pi} \cos^2\varphi d\varphi \right)\left( \int_0^{\pi} \sin^3\theta d\theta \right)\left( \int_0^1 r^4 dr \right) \\ &=\left( \int_0^{2\pi}\frac{1+\cos 2\varphi}{2}d\varphi \right)\left( \int_0^{\pi}\frac{3\sin\theta-\sin3\theta}{4}d\theta \right)\left[\frac{1}{5}r^5 \right]^1_0 \\ &=\frac{1}{5}\left[ \frac{1}{2}\cdot \varphi+\frac{1}{2}\cdot \frac{1}{2}\sin 2\varphi \right]^{2\pi}_0\left[ -\frac{3}{4}\cos \theta+\frac{1}{4}\cdot \frac{1}{3}\cos 3\theta \right]^{\pi}_0 \\ &=\frac{4}{15}\pi \end{align} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

