こんにちは、ひかりです。
今回は微分積分学から多変数関数の積分と累次積分について解説していきます。
この記事では以下のことを紹介します。
- 2重積分の定義について
- 累次積分の計算について
- 累次積分の積分順序の交換について
2重積分の定義
多変数関数の微分に続いて、多変数関数の積分についても学んでいきましょう。
微分のときと同様に2変数関数について扱いますが、3変数以上になっても変わりません。
まず、2変数関数の積分を1変数関数と同じようにリーマン和を用いて定義します。
\( D \) を \( \mathbb{R}^2 \) 内の(つまり \( xy \) 平面内の)有界な集合とします。
そして、
$$ D\subset R=[a,b]\times [c,d] $$
となる長方形 \( R \) をとります。
(つまり、 \( (x,y)\in R \) というのは、 \( x\in [a,b] \) かつ \( y\in [c,d] \) であるということです。)
このとき、区間 \( [a,b] \) と \( [c,d] \) をそれぞれ \( m \) 個と \( n \) 個に分割していきます。
その分割を
$$ \Delta: \ a=x_0<x_1<\cdots<x_m=b, \quad c=y_0<y_1<\cdots<y_n=d $$
と表します。また、次の記号を定めます。
$$ |\Delta|=\max \{ x_i-x_{i-1}, \ y_j-y_{j-1}|1≦i≦m, \ 1≦j≦n \} $$
$$ R_{ij}=[x_{i-1},x_i]\times [y_{j-1},y_j], \quad |R_{ij}|=(x_i-x_{i-1})(y_j-y_{j-1}) $$
また、関数 \( F(x,y) \) を次のように定めます。
$$ F(x,y)=\begin{cases} f(x,y) & (x,y)\in D \\ 0 & (x,y)\in R \backslash D \quad (RからDを除いた集合) \end{cases} $$
このとき、 \( (\xi_i,\eta_j)\in R_{ij} \) を選んだときの \( f \) のリーマン和 \( R[\{(\xi_i,\eta_j)\},\Delta,f] \) を次で定めます。
$$ R[\{(\xi_i,\eta_j)\},\Delta,f]=\sum_{i=1}^m\sum_{j=1}^nF(\xi_i,\eta_j)|R_{ij}| $$
(つまり、分割によってできた各直方体の面積の和をリーマン和とよんでいます)
このリーマン和を用いて、次のように(リーマンの意味での)2重積分を定義します。
\( |\Delta|\to 0 \) のとき、 \( (\xi_i,\eta_j) \) の選び方によらない数 \( J \) が存在して、
$$ \lim_{|\Delta|\to0}R[\{(\xi_i,\eta_j)\},\Delta,f]=J $$
となるとき、 \( f \) は \( D \) 上(リーマン)積分可能という。
(これは区間の分割をどんどん細分化していくことに相当します)
また、このとき \( J \) を
$$ \iint_Df(x,y)dxdy $$
とかいて、 \( f \) の \( D \) 上での2重積分という。
1変数関数の積分と同様に次のような性質が成り立ちます。
\( f, \ g \) を \( D \) 上積分可能とする。
(1) $$ \iint_Dkf(x,y)dxdy=k\iint_Df(x,y)dxdy \quad (k:定数) $$
(2) $$ \iint_D\{ f(x,y)+g(x,y) \} dxdy=\iint_Df(x,y)dxdy+\iint_Dg(x,y)dxdy $$
(3) $$ \iint_D\{ f(x,y)-g(x,y) \} dxdy=\iint_Df(x,y)dxdy-\iint_Dg(x,y)dxdy $$
(4) \( D=D_1\cup D_2, \ D_1\cap D_2=\emptyset \) であるならば、
$$ \iint_{D_1}f(x,y)dxdy+\iint_{D_2}f(x,y)dxdy=\iint_Df(x,y)dxdy $$
また、次のような性質も成り立ちます。
\( f, \ g \) を \( D \) 上積分可能とする。
(1) すべての \( (x,y)\in D \) に対して、 \( f(x,y)≧0 \) であるとき、次が成り立つ。
$$ \iint_Df(x,y)dxdy≧0 $$
(2) すべての \( (x,y)\in D \) に対して、 \( f(x,y)≧g(x,y) \) であるとき、次が成り立つ。
$$ \iint_Df(x,y)dxdy≧\iint_Dg(x,y)dxdy $$
(3) \( |f| \) も \( D \) 上積分可能であり、次が成り立つ。
$$ \iint_D|f(x,y)|dxdy≧\left| \iint_Df(x,y)dxdy \right| $$
さらに、積分に関する平均値の定理も同様に成り立ちます。
\( f \) が \( D \) 上で連続であるとする。このとき、
$$ \iint_Df(x,y)dxdy=f(\xi,\eta)\iint_Ddxdy $$
をみたす \( (\xi,\eta)\in D \) が存在する。
最後に、積分可能性の条件を1つ紹介します。
関数 \( f \) が閉立方体 \( R=[a,b]\times [c,d] \) 上で連続であるとき、 \( f \) は \( R \) 上で積分可能である。
累次積分の計算
2重積分を定義しましたが、このままでは計算ができません。
よって、計算できるように次の定理を与えます。
関数 \( f(x,y) \) は長方形 \( R=[a,b]\times [c,d] \) 上有界かつ連続であるとする。
(関数 \( f \) が有界であるとは、 \( f \) の値域の集合が有界であるということ)
(1) \( y\in [c,d] \) を固定したとき、 \( x \) の関数として \( [a,b] \) 上積分可能であるとする。
このとき、
$$ \int_a^bf(x,y)dx $$
は \( y \) について \( [c,d] \) 上積分可能であり、次が成り立つ。
$$ \iint_Rf(x,y)dxdy=\int_c^d \left(\int_a^b f(x,y)dx\right) dy $$
(2) \( x\in [a,b] \) を固定したとき、 \( y \) の関数として \( [c,d] \) 上積分可能であるとする。
このとき、
$$ \int_c^df(x,y)dy $$
は \( x \) について \( [a,b] \) 上積分可能であり、次が成り立つ。
$$ \iint_Rf(x,y)dxdy=\int_a^b \left(\int_c^d f(x,y)dy\right) dx $$
$$ \int_c^d \left(\int_a^b f(x,y)dx\right) dy $$
のように、1変数ずつ分けて積分することを累次積分といいます。
定理5の証明(気になる方だけクリックしてください)
(1)のみ示します。
(1) まず、 \( R=[a,b]\times [c,d] \) の分割を次で表します。
$$ \Delta: \ a=x_0<x_1<\cdots<x_m=b, \quad c=y_0<y_1<\cdots<y_n=d $$
また、関数 \( F(y) \) を次で定めます。
$$ F(y)=\int_a^bf(x,y)dx $$
このとき、分割の定め方から、
$$ F(y)=\sum_{i=1}^m\int_{x_{i-1}}^{x_i}f(x,y)dx $$
となります。
\( f \) が連続であるので、 \( \eta_j\in [y_{j-1},y_j] \) をとり、 \( x \) 変数に対して1変数関数の積分に関する平均値の定理を用いると、
$$ \int_{x_{i-1}}^{x_i}f(x,\eta_j)dx=(x_i-x_{i-1})f(\xi_i,\eta_j) $$
をみたす \( \xi_i\in [x_{i-1},x_i] \) が存在します。
よって、 \( i \) について \( 1 \) から \( m \) まで和をとると、
$$ F(\eta_j)=\sum_{i=1}^m(x_i-x_{i-1})f(\xi_i,\eta_j) $$
両辺に \( y_j-y_{j-1} \) をかけて、 \( j \) について \( 1 \) から \( n \) まで和をとると、
$$ \sum_{j=1}^n(y_j-y_{j-1})F(\eta_j)=\sum_{i=1}^m\sum_{j=1}^n(x_i-x_{i-1})(y_j-y_{j-1})f(\xi_i,\eta_j) $$
これは、1変数および2変数のリーマン和の定義より、次のように表せます。
$$ R[\{\eta_j\},\Delta_0,F]=R[{(\xi_i,\eta_j)},\Delta,f] \tag{1} $$
ここで、分割 \( \Delta_0 \) とは、
$$ \Delta_0: \ c=y_0<y_1<\cdots<y_n=d $$
\( f \) が \( R \) 上連続であることと定理4より、 \( |\Delta|\to 0 \) とすると、式(1)の右辺は
$$ \iint_Rf(x,y)dxdy $$
に収束します。
このとき、 \( 0<|\Delta_0|≦|\Delta| \) であるので、はさみうちの原理より、 \( |\Delta_0|\to 0 \) となります。
したがって、
$$ \lim_{|\Delta_0|\to 0}R[\{\eta_j\},\Delta_0,F]=\iint_Rf(x,y)dxdy $$
よって、 \( F \) は \( [c,d] \) 上で積分可能であり、
$$ \lim_{|\Delta_0|\to 0}R[\{\eta_j\},\Delta_0,F]=\int_c^d F(y) dy=\int_c^d \left(\int_a^b f(x,y)dx\right) dy $$
まとめると、
$$ \iint_Rf(x,y)dxdy=\int_c^d \left(\int_a^b f(x,y)dx\right) dy $$
累次積分は片方の変数を定数だと思って積分することにより、1変数関数の積分と同じように計算することができます。
(1) \( R=[0,3]\times [0,2] \) とするとき、 \( \displaystyle \iint_Rxy^2dxdy \) を求める。
定理5(1)より、
$$ \iint_Rxy^2dxdy=\int_0^2\left( \int_0^3 xy^2dx \right) dy $$
となる。この積分は片方の変数を定数だと思って積分すればよいので、
$$ \begin{align} \int_0^2\left( \int_0^3 xy^2dx \right) dy&=\int_0^2 \left[ \frac{1}{2}x^2y^2 \right]^3_0 dy \quad (yを定数だと思ってxで積分する) \\ &=\int_0^2 \frac{9}{2}y^2dy=\left[ \frac{3}{2}y^3 \right]^2_0=12 \end{align} $$
(2) \( R=[1,3]\times [1,2] \) とするとき、 \( \displaystyle \iint_R(x+2y)dxdy \) を求める。
定理5(2)より、
$$ \iint_R(x+2y)dxdy=\int_1^3\left( \int_1^2 (x+2y)dy \right) dx $$
となる。この積分は片方の変数を定数だと思って積分すればよいので、
$$ \begin{align} \int_1^3\left( \int_1^2 (x+2y)dy \right) dx&=\int_1^3 \left[ xy+y^2 \right]^2_1 dx \quad (xを定数だと思ってyで積分する) \\ &=\int_1^3 (x+3)dx=\left[ \frac{1}{2}x^2+3x \right]^3_1=10 \end{align} $$
定理5をもう少し一般化してみましょう。
\( \varphi_1(x), \varphi_2(x) \) を区間 \( I=[a,b] \) 上の連続関数で、 \( I \) 上 \( \varphi_1(x)≦\varphi_2(x) \) とする。そして、
$$ D=\{ (x,y)|x\in I, \ \varphi_1(x)≦y≦\varphi_2(x) \} $$
とおきます。
このとき、関数 \( f(x,y) \) が \( D \) 上で有界かつ連続であれば、次が成り立つ。
$$ \iint_Df(x,y)dxdy=\int_a^b\left( \int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy \right) dx $$
これだけだと、よくわからないと思いますので、例を見ていきましょう。
(1) $$ D=\{ (x,y)|x\in [1,2], \ x-1≦y≦-x+3 \} $$
のとき、 \( \displaystyle \iint_D(x+2y)dxdy \) を求める。
定理6より、
$$ \iint_D(x+2y)dxdy=\int_1^2\left( \int_{x-1}^{-x+3}(x+2y)dy \right) dx $$
よって、
$$ \begin{align} &\int_1^2\left( \int_{x-1}^{-x+3}(x+2y)dy \right) dx=\int_1^2\left[xy+y^2\right]^{-x+3}_{x-1}dx \\ &=\int_1^2\{ \{ x(-x+3)+(-x+3)^2\}-\{ x(x-1)+(x-1)^2\}\} dx \\ &=\int_1^2\{ (-3x+9)-(2x^2-3x+1)\}dx \\ &=\int_1^2(-2x^2+8)dx=\left[ -\frac{2}{3}x^3+8x \right]^2_1=\frac{10}{3} \end{align} $$
(2) $$ D=\{ (x,y)|y\in[1,2], \ y≦x≦y^2 \} $$
のとき、 \( \displaystyle \iint_D\frac{1}{x+y}dxdy \) を求める。
定理6より、
$$ \iint_D\frac{1}{x+y}dxdy=\int_1^2\left( \int_{y}^{y^2}\frac{1}{x+y}dx \right) dy $$
よって、
$$ \begin{align} &\int_1^2\left( \int_{y}^{y^2}\frac{1}{x+y}dx \right) dy=\int_1^2\left[ \log(x+y) \right]^{y^2}_y dy \\ &=\int_1^2(\log(y^2+y)-\log 2y)dy \\ &=\int_1^2\log\frac{y(y+1)}{2y}dy \quad (対数の差の公式) \\ &=\int_1^2\log\frac{y+1}{2}dy \\ &=\int_1^2(\log(y+1)-\log 2) dy \quad (再び対数の差の公式で戻した) \\ &=\left[ (y+1)\log (y+1)-(y+1)-(\log2)y \right]^2_1 \\ &=(3\log 3-3-2\log 2)-(2\log 2-2-\log 2)=3\log 3-3\log 2-1 \end{align} $$
累次積分の積分順序の交換
定理6より、累次積分の積分順序の交換に関する定理が得られます。
\( \varphi_1(x), \varphi_2(x) \) を区間 \( I=[a,b] \) 上の連続関数で、 \( I \) 上 \( \varphi_1(x)≦\varphi_2(x) \) とする。
また、 \( \psi_1(y), \psi_2(y) \) を区間 \( J=[c,d] \) 上の連続関数で、 \( J \) 上 \( \psi_1(y)≦\psi_2(y) \) とする。
ここで、
$$ \begin{align} D&=\{ (x,y)|x\in I, \ \varphi_1(x)≦y≦\varphi_2(x) \} \\ &=\{ (x,y)|y\in J, \ \psi_1(y)≦x≦\psi_2(y) \} \end{align} $$
と表せるとします。
このとき、関数 \( f(x,y) \) が \( D \) 上で有界かつ連続であれば、次が成り立つ。
$$ \int_a^b\left( \int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy \right) dx=\int_c^d\left( \int_{\psi_1(y)}^{\psi_2(y)}f(x,y)dx \right) dy $$
$$ D=\{ (x,y)|x\in[0,1], \ x^2≦y≦\sqrt{x} \} $$
のとき、 \( \displaystyle \iint_Dx^3ydxdy \) を2通りの方法で求める。
まず、 \( y \) 変数の積分を先におこなってから、 \( x \) 変数の積分をおこなう。
$$ \begin{align} \iint_Dx^3ydxdy&=\int_0^1\left( \int_{x^2}^{\sqrt{x}} x^3y dy \right) dx=\int_0^1\left[ \frac{1}{2}x^3y^2 \right]^{\sqrt{x}}_{x^2}dx \\ &=\frac{1}{2}\int_0^1(x^4-x^7)dx=\frac{1}{2}\left[ \frac{1}{5}x^5-\frac{1}{8}x^8 \right]^1_0=\frac{3}{80} \end{align} $$
次に、 \( x \) 変数の積分を先におこなってから、 \( y \) 変数の積分をおこなう。
そのために、 \( D \) を書き換える。 \( D \) を図示すると次のような集合となる。
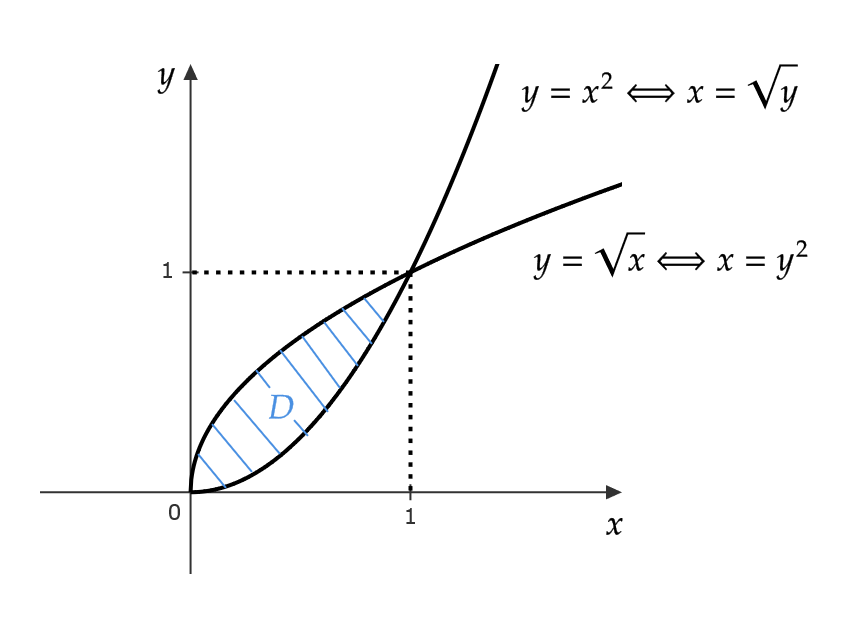
よって、
$$ \begin{align} D&=\{ (x,y)|x\in[0,1], \ x^2≦y≦\sqrt{x} \} \\ &=\{ (x,y)|y\in[0,1], \ y^2≦x≦\sqrt{y} \} \end{align} $$
と表すことができる。
( \( y \) 軸を下にするようにグラフを90度傾けるとわかりやすいです)
したがって、
$$ \begin{align} \iint_Dx^3ydxdy&=\int_0^1\left( \int_{y^2}^{\sqrt{y}} x^3y dx \right) dy=\int_0^1\left[ \frac{1}{4}x^4y \right]^{\sqrt{y}}_{y^2}dy \\ &=\frac{1}{4}\int_0^1(y^3-y^9)dy=\frac{1}{4}\left[ \frac{1}{4}y^4-\frac{1}{10}y^{10} \right]^1_0=\frac{3}{80} \end{align} $$
よって、どちらの方法で積分したとしても
$$ \iint_Dx^3ydxdy=\frac{3}{80} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

