こんにちは、ひかりです。
今回は微分積分学から偏微分可能性と偏導関数について解説していきます。
この記事では以下のことを紹介します。
- 偏微分可能性と偏導関数について
- 偏微分の図形的意味について
- 高階偏導関数とシュワルツの定理について
偏微分可能性と偏導関数
ここでは話を簡単にするために、2変数関数 \( f(x,y) \) の偏微分について扱いますが、3変数以上の関数についても同様のことが成り立ちます。
1変数の場合と異なり、2変数の場合は \( x \) と \( y \) の2つの変数に関する微分というものが考えられます。
$$ \lim_{h\to0}\frac{f(a+h,b)-f(a,b)}{h} $$
を関数 \( f(x,y) \) の \( (x,y)=(a,b) \) における \( x \) に関する偏微分係数といい、
$$ \frac{\partial f}{\partial x}(a,b), \quad f_x(a,b) $$
と表す。また、このとき \( f(x,y) \) は \( (x,y)=(a,b) \) で \( x \) に関して偏微分可能であるという。
同様に、
$$ \lim_{h\to0}\frac{f(a,b+h)-f(a,b)}{h} $$
を関数 \( f(x,y) \) の \( (x,y)=(a,b) \) における \( y \) に関する偏微分係数といい、
$$ \frac{\partial f}{\partial y}(a,b), \quad f_y(a,b) $$
と表す。また、このとき \( f(x,y) \) は \( (x,y)=(a,b) \) で \( y \) に関して偏微分可能であるという。
\( D\subset \mathbb{R}^2 \) に対して、\( f(x,y) \) がすべての \( (x,y)\in D \) で偏微分可能であるとき、 \( f \) は \( D \) 上偏微分可能であるという。
このとき、 \( D \) 上で定義される関数 \( f_x(x,y), \ f_y(x,y) \) をそれぞれ \( x,y \) に関する偏導関数という。
(1) \( f(x,y)=\frac{x}{y} \) のとき、 \( f_x,f_y \) を求める。
\( f_x \) は \( y \) を定数だと思い \( f(x,y) \) を \( x \) の1変数関数だとみて1変数関数の微分を行うことと同じなので、
$$ f_x(x,y)=\frac{(x)’}{y}=\frac{1}{y} $$
同様に、 \( f_y \) は \( x \) を定数だと思い \( f(x,y) \) を \( y \) の1変数関数だとみて1変数関数の微分を行うことと同じなので、
$$ f_y(x,y)=\frac{x}{(y)’}=-\frac{x}{y^2} $$
(2) \( f(x,y)=x\log y \) のとき、 \( f_x(4,2), \ f_y(4,2) \) を求める。
まず、偏導関数を求めると、
$$ f_x(x,y)=(x)’\log y=\log y, \quad f_y(x,y)=x(\log y)’=\frac{x}{y} $$
よって、点 \( (4,2) \) を代入すると、
$$ f_x(4,2)=\log 2, \quad f_y(4,2)=\frac{4}{2}=2 $$
(3) 次の関数を考える。
$$ f(x,y)=\begin{cases} \frac{x^5}{(y-x^2)^2+x^6} & ((x,y)\not=(0,0) のとき) \\ 0 & ((x,y)=(0,0) のとき) \end{cases} $$
これの原点 \( (0,0) \) での偏微分係数を定義通りに求める。
\( h\not=0 \) のとき、
$$ f(h,0)=\frac{h^5}{(0-h^2)^2+h^6}=\frac{h^5}{h^4+h^6} $$
よって、
$$ f_x(0,0)=\lim_{h\to0}\frac{f(h,0)-f(0,0)}{h}=\lim_{h\to0}\frac{1}{h}\frac{h^5}{h^4+h^6}=\lim_{h\to0}\frac{1}{1+h^2}=1 $$
また、
$$ f(0,h)=\frac{0^5}{(h-0^2)^2+0^6}=0 $$
より、
$$ f_y(0,0)=\lim_{h\to0}\frac{f(0,h)-f(0,0)}{h}=\lim_{h\to0}\frac{0-0}{h}=0 $$
したがって、 \( f_x(0,0)=1, \ f_y(0,0)=0 \) より、この関数は原点 \( (0,0) \) で偏微分可能である。
しかし、微分積分学07の例6の(2)より、この関数は原点 \( (0,0) \) で連続ではない。
よって、偏微分可能であっても連続であるとは、一般にはいえない。
偏微分の図形的意味
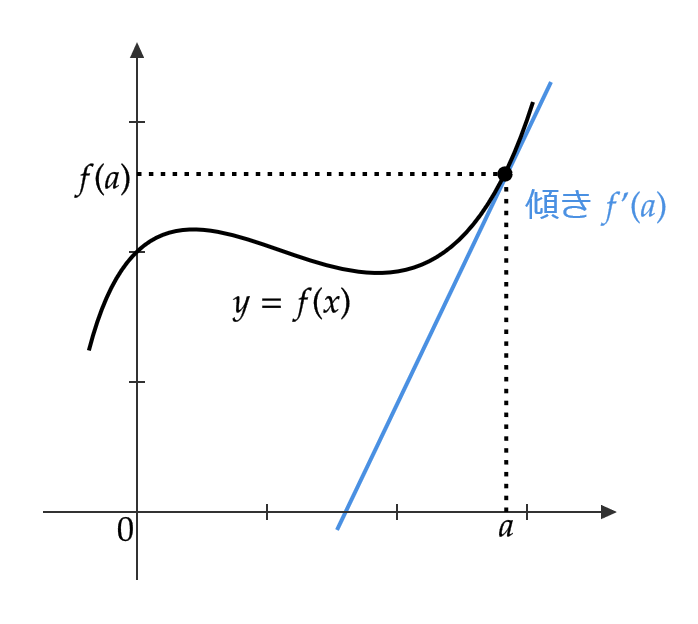
1変数関数の場合は、微分とはその関数の接線の傾きを求めるものでした。
では、2変数関数の偏微分は何を求めるものなのでしょうか。それについて考えていきましょう。
そもそも2変数関数 \( z=f(x,y) \) とはどのようなグラフとなるかを考えると一般に3次元空間上の平面となります。
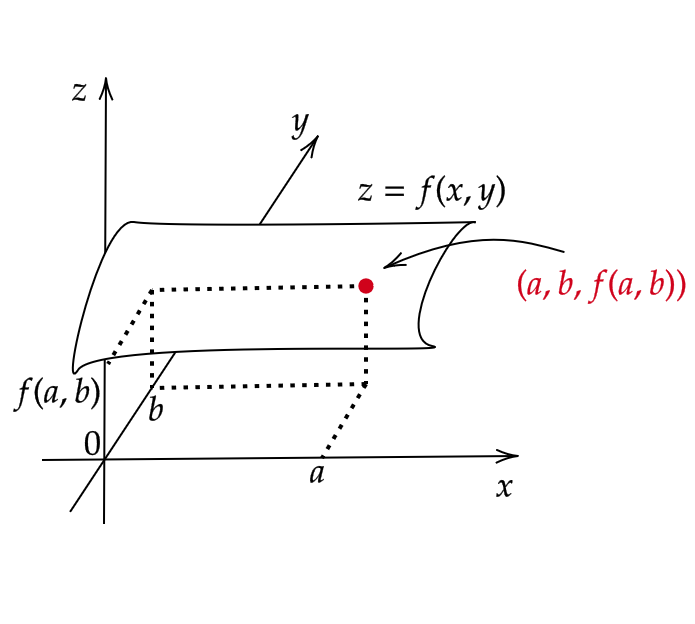
ここで、点 \( (a,b) \) での \( x\) に関する偏微分係数 \( f_x(a,b) \) を考えます。
この偏微分係数は定義から、 \( y=b \) は固定した上での \( f(x,b) \) の \( x=a \) での変化の仕方を表しているわけです。
そこで、点 \( (x,b,f(x,b)) \) に注目すると、これは \( y=b \) という平面上の点となります。
(いま、 \( xyz \) 空間を考えているので、 \( y=b \) は平面となります。)
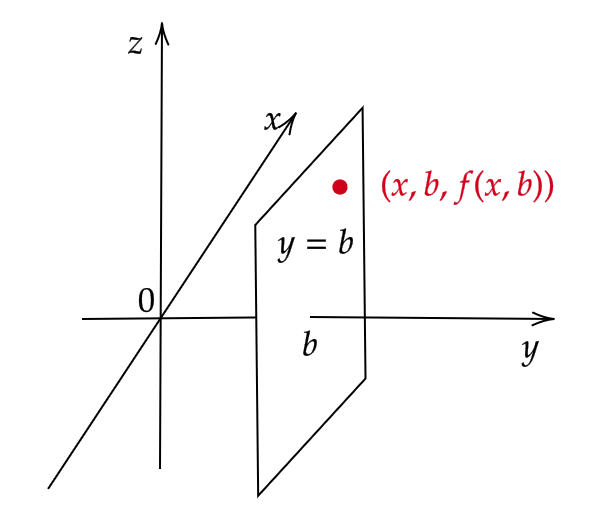
さらに、 \( z=f(x,b) \) であるので、 \( y=b \) と \( z=f(x,y) \) の交わるところ、つまり \( y=b \) の平面で \( z=f(x,y) \) を切ったときの断面図上の点ということになります。
この断面図(曲線)を \( C(x) \) とおきます。
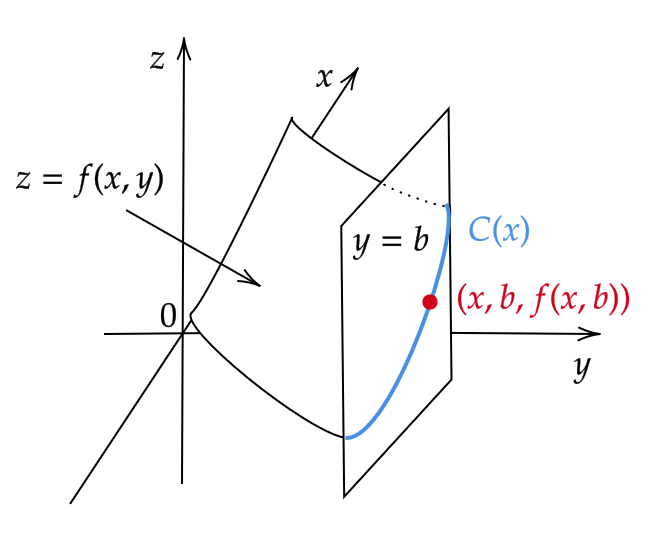
この曲線 \( C(x) \) というのは、 \( y=b \) という平面上に描かれているのでこれは1変数関数としてみることができます。
よって、 \( f_x(a,b) \) とはこの曲線の \( x=a \) での値 \( C(a) \) における接線の傾きを表すことになります。
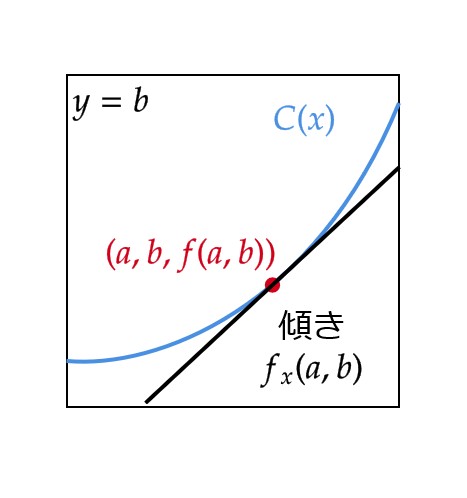
また、 \( f_y(a,b) \) についても平面 \( x=a \) 上の \( z=f(x,y) \) の断面図の曲線 \( C'(y) \) を考えて、その \( y=b \) での値 \( C'(b) \) における接線の傾きを表します。
高階偏導関数とシュワルツの定理
高階偏導関数
一変数関数の場合と同様に、高階の微分について見ていきましょう。
\( f_x \) が \( x \) に関して偏微分可能であれば、 \( \frac{\partial f_x}{\partial x} \) を考えることができます。これを
$$ \frac{\partial^2 f}{\partial x^2}, \quad \frac{\partial}{\partial x}\left( \frac{\partial f}{\partial x} \right), \quad \left( \frac{\partial}{\partial x} \right)^2f, \quad f_{xx} $$
などと表します。同様に、
$$ f_{xy}=\frac{\partial}{\partial y}\left( \frac{\partial f}{\partial x} \right), \quad f_{yx}=\frac{\partial}{\partial x}\left( \frac{\partial f}{\partial y} \right), \quad f_{yy}=\frac{\partial}{\partial y}\left( \frac{\partial f}{\partial y} \right) $$
も考えられます。
これらを \( f \) の2階偏導関数といいます。3階以上の偏導関数についても同様に定められます。
(1) \( f(x,y)=\tan^{-1}\frac{y}{x} \) のとき、 \( f_{xx}, \ f_{xy}, \ f_{yx}, \ f_{yy} \) を求める。
\( u=\frac{y}{x} \) とおいて、合成関数の微分を用いると、
$$ f_x=\frac{d}{du}(\tan^{-1}u)\cdot \frac{\partial u}{\partial x}=\frac{1}{1+u^2}\cdot \frac{\partial }{\partial x}\left(\frac{y}{x} \right)=\frac{1}{1+\left( \frac{y}{x}\right)^2}\cdot \left( -\frac{y}{x^2} \right)=\frac{-y}{x^2+y^2} $$
$$ f_y=\frac{d}{du}(\tan^{-1}u)\cdot \frac{\partial u}{\partial y}=\frac{1}{1+u^2}\cdot \frac{\partial }{\partial y}\left(\frac{y}{x} \right)=\frac{1}{1+\left( \frac{y}{x}\right)^2}\cdot \left( \frac{1}{x} \right)=\frac{x}{x^2+y^2} $$
よって、
$$ f_{xx}=\frac{\partial f_x}{\partial x}=\frac{\partial}{\partial x}\left( \frac{-y}{x^2+y^2} \right)=(-y)\cdot \left\{ -\frac{1}{(x^2+y^2)^2} \right\}\cdot 2x=\frac{2xy}{(x^2+y^2)^2} $$
$$ \begin{align} f_{xy}&=\frac{\partial f_x}{\partial y}=\frac{\partial}{\partial y}\left( \frac{-y}{x^2+y^2} \right) \\ &=\frac{(-y)_y(x^2+y^2)-(-y)(x^2+y^2)_y}{(x^2+y^2)^2} \\ &=\frac{-(x^2+y^2)+y(2y)}{(x^2+y^2)^2}=\frac{-x^2+y^2}{(x^2+y^2)^2} \end{align} $$
$$ \begin{align} f_{yx}&=\frac{\partial f_y}{\partial x}=\frac{\partial}{\partial x}\left( \frac{x}{x^2+y^2} \right) \\ &=\frac{(x)_x(x^2+y^2)-x(x^2+y^2)_x}{(x^2+y^2)^2} \\ &=\frac{x^2+y^2-x(2x)}{(x^2+y^2)^2}=\frac{-x^2+y^2}{(x^2+y^2)^2} \end{align} $$
$$ f_{yy}=\frac{\partial f_y}{\partial y}=\frac{\partial}{\partial y}\left( \frac{x}{x^2+y^2} \right)=x\cdot \left\{ -\frac{1}{(x^2+y^2)^2} \right\}\cdot 2y=\frac{-2xy}{(x^2+y^2)^2} $$
この場合は \( f_{xy}=f_{yx} \) となる。
(2) 次の関数を考える。
$$ f(x,y)=\begin{cases} \frac{xy(x^2-y^2)}{x^2+y^2} & ((x,y)\not=(0,0) のとき) \\ 0 & ((x,y)\not=(0,0) のとき) \end{cases} $$
このとき、 \( f_{xy}(0,0), \ f_{yx}(0,0) \) を求める。
まず、 \( (x,y)\not=(0,0) \) のときは、
$$ \begin{align} f_x(x,y)&=\frac{\{xy(x^2-y^2)\}_x(x^2+y^2)-\{xy(x^2-y^2)\}(x^2+y^2)_x}{(x^2+y^2)^2} \\ &=\frac{\{y(x^2-y^2)+xy(2x)\}(x^2+y^2)-\{xy(x^2-y^2)\}(2x)}{(x^2+y^2)^2} \\ &=\frac{(x^2y-y^3+2x^2y)(x^2+y^2)-(x^3y-xy^3)(2x)}{(x^2+y^2)^2} \\ &=\frac{x^4y+4x^2y^3-y^5}{(x^2+y^2)^2} \end{align} $$
同様に、
$$ f_y(x,y)=\frac{x^5-4x^3y^2-xy^4}{(x^2+y^2)^2} $$
次に、 \( (x,y)=(0,0) \) のときは、偏導関数の定義に従って、
$$ f_x(0,0)=\lim_{h\to0}\frac{f(h,0)-f(0,0)}{h}=\lim_{h\to0}\frac{0-0}{h}=0 $$
$$ f_y(0,0)=\lim_{h\to0}\frac{f(0,h)-f(0,0)}{h}=\lim_{h\to0}\frac{0-0}{h}=0 $$
よって、
$$ f_{xy}(0,0)=\lim_{h\to0}\frac{f_x(0,h)-f_x(0,0)}{h}=\lim_{h\to0}\frac{-\frac{h^5}{h^4}-0}{h}=-1 $$
$$ f_{yx}(0,0)=\lim_{h\to0}\frac{f_y(h,0)-f_y(0,0)}{h}=\lim_{h\to0}\frac{\frac{h^5}{h^4}-0}{h}=1 $$
この場合は、 \( f_{xy}(0,0)\not=f_{yx}(0,0) \) となる。
1変数関数の場合と同様にして、 \( C^n \) 級を定義します。
関数 \( f(x,y) \) が \( f \) の定義域 \( D \) 上連続であるとき、 \( f \) は \( D \) 上で \( C^0 \) 級関数であるという。
また、自然数 \( n \) に対して、 \( f \) が \( n \) 階までのあらゆる偏導関数をもち、それらがすべて \( D \) 上連続であるとき、 \( f \) は \( D \) 上で \( C^n \) 級関数であるという。
さらに、 \( f \) が \( D \) 上で何回でも偏微分可能でありすべての偏導関数が \( D \) 上連続のとき、 \( f \) は \( D \) 上で \( C^{\infty} \) 級関数であるという。
シュワルツの定理
一般に \( f_{xy} \) と \( f_{yx} \) は等しくないといいましたが、ではどのようなときに \( f_{xy}=f_{yx} \) となるのでしょうか。
それに対する1つの答えとして、シュワルツの定理があります。
点 \( (a,b) \) のまわりで \( f_x, \ f_y, \ f_{xy} \) が存在して、 \( f_{xy} \) が点 \( (a,b) \) で連続であるならば、 \( f_{yx}(a,b) \) も存在して、
$$ f_{xy}(a,b)=f_{yx}(a,b) $$
定理1の証明(気になる方だけクリックしてください)
まず、関数 \( g(x,y) \) を次のように定めます。
$$ g(x,y)=f(x,y)-f(x,b) $$
十分小さく \( h,k \) をとって、 \( g \) の \( x \) 変数に関して1変数関数の平均値の定理を用いると、
$$ \begin{align} g(a+h,b+k)-g(a,b+k)&=hg_x(c,b+k) \quad (c \ は \ a \ と \ a+h \ の間にある) \\ &=h\{ f_x(c,b+k)-f_x(c,b)\} \end{align} $$
さらに、 \( f_x(c,y) \) の \( y \) 変数に関して1変数関数の平均値の定理を用いると、
$$ \begin{align} g(a+h,b+k)-g(a,b+k)&=h\{ f_x(c,b+k)-f_x(c,b)\} \\ &=hkf_{xy}(c,d) \quad (d \ は \ b \ と \ b+k \ の間にある) \end{align} \tag{1} $$
よって、
$$ \lim_{k\to0}\frac{g(x,b+k)}{k}=\lim_{k\to0}\frac{f(x,b+k)-f(x,b)}{k}=f_y(x,b) $$
に注意して、式(1)の最両辺を \( k\to0 \) とすると、
$$ f_y(a+h,b)-f_y(a,b)=h\lim_{k\to0}f_{xy}(c,d) $$
したがって、
$$ f_{yx}(a,b)=\lim_{h\to0}\frac{f_y(a+h,b)-f_y(a,b)}{h}=\lim_{h\to0}\left\{ \lim_{k\to0}f_{xy}(c,d)\right\} $$
ここで、微分積分学07の記事の定理4より、
$$ \lim_{h\to0}\left\{ \lim_{k\to0}f_{xy}(c,d)\right\}=\lim_{(h,k)\to(0,0)}f_{xy}(c,d) $$
よって、
$$ \begin{align} f_{yx}(a,b)&=\lim_{(h,k)\to(0,0)}f_{xy}(c,d) \\ &=f_{xy}(a,b) \quad ((h,k)\to(0,0) \ のとき \ (c,d)\to(a,b) \ となる) \end{align} $$
シュワルツの定理より、次のことが成り立ちます。
\( f(x,y) \) が \( C^n \) 級関数であれば、 \( n \) 階までの偏導関数は偏微分の順序によらずにすべて一致する。
例えば、 \( f \) が \( C^3 \) 級であれば、
$$ f_{xxy}=f_{xyx}=f_{yxx}, \quad f_{xyy}=f_{yxy}=f_{yyx} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

