こんにちは、ひかりです。
今回は微分積分学から多変数関数の極限と連続性について解説していきます。
この記事では以下のことを紹介します。
- 2変数関数の定義と \( xy \) 平面の集合に関するさまざまな概念について
- 2変数関数の極限について
- 2変数関数の連続性について
2変数関数の定義とxy平面の集合に関するさまざまな概念
2変数関数の定義
今回から多変数の関数について扱っていきます。
説明を簡単にするために2変数関数に限定して紹介しますが、3変数以上になっても同様のことが成り立ちます。
以下、 \( xy \) 平面のことを \( \mathbb{R}^2 \) とかくことにします。
2変数関数 \( f \) とは、 \( xy \) 平面 \( \mathbb{R}^2 \) の部分集合 \( D \) 上の点 \( (x,y) \) に対して、実数 \( f(x,y) \) がただ一つ定まるものをいう。
このとき、 \( D \) を関数 \( f(x,y) \) の定義域といい、 \( D \) 上を動く値 \( f(x,y) \) の集合を関数 \( f(x,y) \) の値域という。
xy 平面の集合に関するさまざまな概念
2変数関数を扱ううえで大事となる \( \mathbb{R}^2 \) 内の集合に関するさまざまな概念について、簡単に紹介していきます。
\( \mathbb{R}^2 \) 内の2点 \( P=(x,y), \ Q=(x’,y’) \) に対して、2点間の距離を \( d(P,Q) \) で表すことにします。つまり、
$$ d(P,Q)=\sqrt{(x-x’)^2+(y-y’)^2} $$
距離は次の性質をみたします。
(1) (距離の正値性)
$$ d(P,Q)≧0, \quad 等号成立は \ P=Q \ のときに限る $$
(2) (距離の対称性)
$$ d(P,Q)=d(Q,P) $$
(3) (三角不等式)
$$ d(P,R)≦d(P,Q)+d(Q,R) \quad (つまり、まわり道をしたほうが距離が長くなる) $$
次に、有界という概念を紹介します。
集合 \( A\subset \mathbb{R}^2 \) (つまり、 \( \mathbb{R}^2 \) 内の部分集合 \( A \) ) が有界であるとは、原点を中心とする十分大きな半径の円が \( A \) を含むようにできることをいう。つまり、
$$ A\subset \{ (x,y)\in \mathbb{R}^2:x^2+y^2≦R^2 \} $$
となるような \( R>0 \) が存在することをいう。
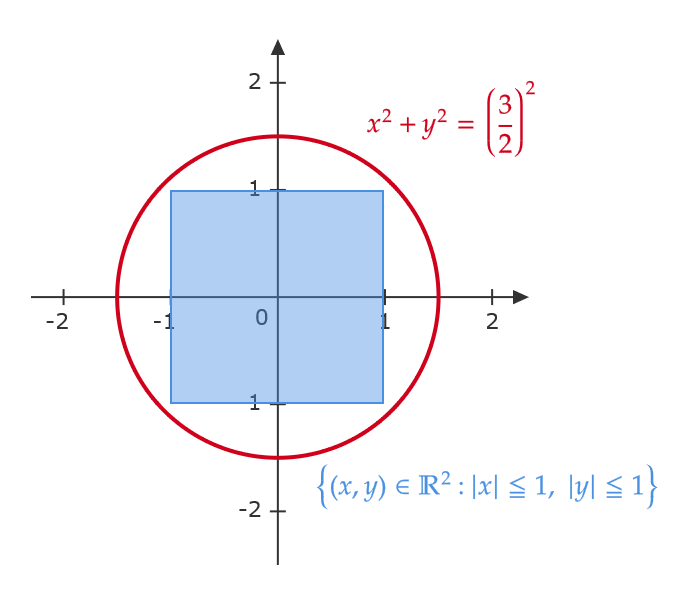
(1) \( A \) を原点を中心とする各辺の長さが2の正方形としたときの有界性を考える。つまり、
$$ A=\{ (x,y)\in\mathbb{R}^2: \ |x|≦1, \ |y|≦1 \} $$
これは原点中心で半径 \( \frac{3}{2} \) の円で覆えるので有界である。つまり、
$$ A\subset \left\{ (x,y)\in \mathbb{R}^2:x^2+y^2≦\left(\frac{3}{2}\right)^2 \right\} $$
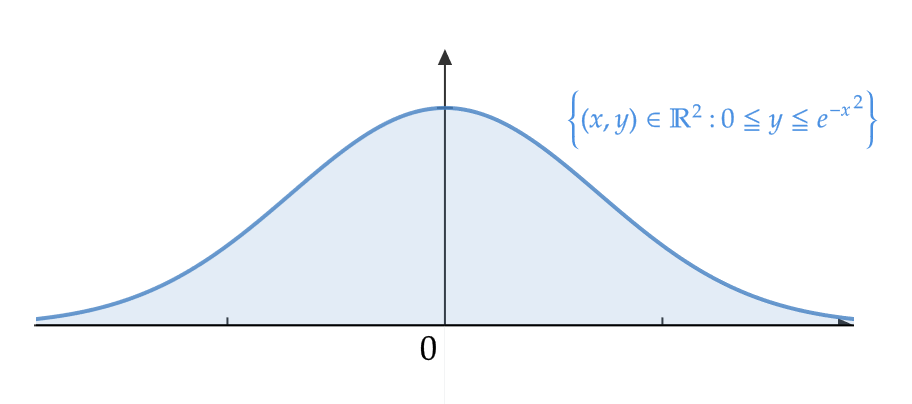
(2) \( A \) を \( y=e^{-x^2} \) と \( x \) 軸で囲まれた図形とする。つまり、
$$ A=\{ (x,y)\in\mathbb{R}^2: \ 0≦y≦e^{-x^2} \} $$
これは原点中心の円で覆うことはできないので、有界ではない。
次に、開集合と閉集合について説明します。
集合 \( A \) の境界を \( \partial A \) と表す。また、 \( A\cup \partial A \) を \( A \) の閉包といい、 \( \overline{A} \) と表す。
さらに、 \( \overline{A}\backslash \partial A \) を \( A \) の内部といい、 \( A^i \) と表す。ただし、 \( A=\emptyset \) の場合は \( \overline{A}=A^i=\emptyset \) とする。
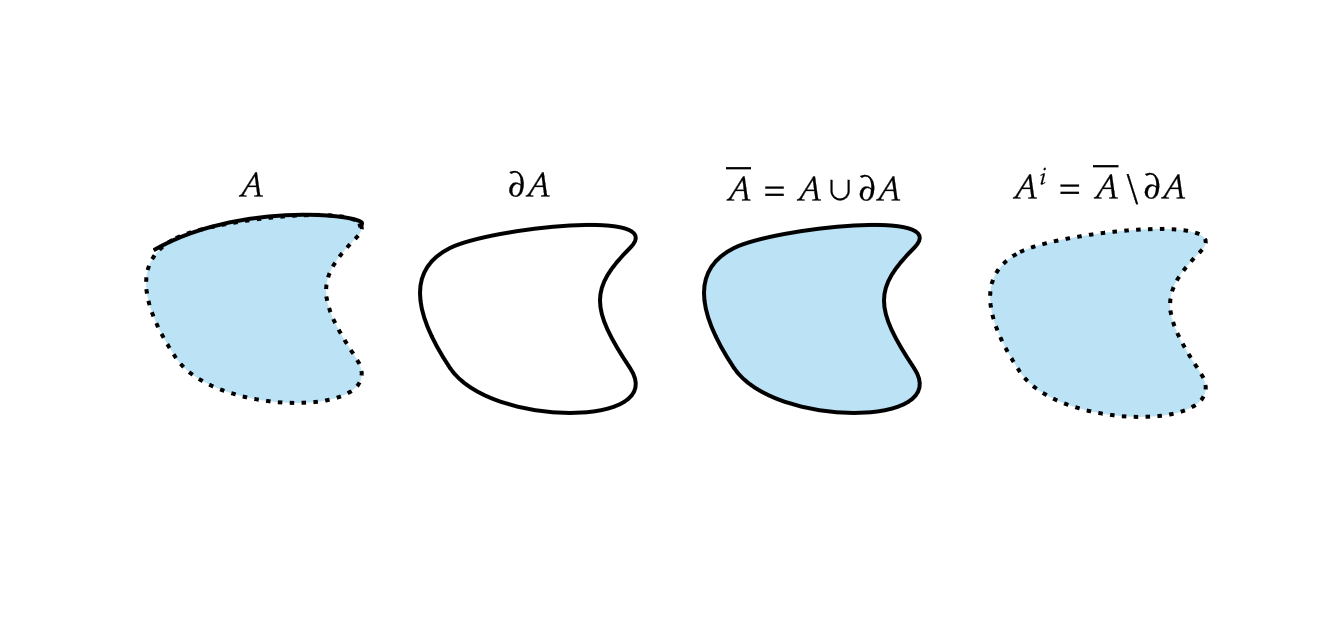
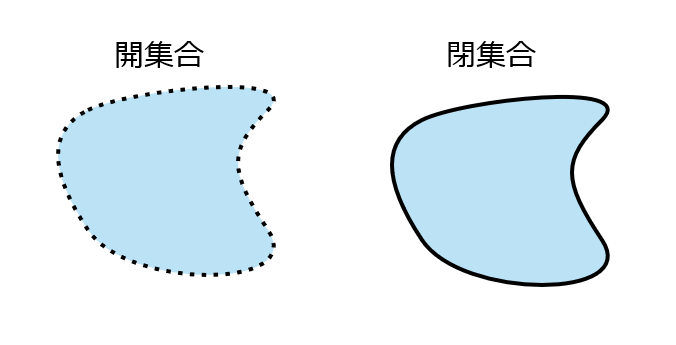
\( A^i=A \) が成り立つとき、 \( A \) を開集合という。
また、 \( \overline{A}=A \) が成り立つとき、 \( A \) を閉集合という。
(1) \( A=\{ (x,y)\in\mathbb{R}^2: \ |x|≦1, \ |y|<1 \} \) とおく。このとき、
$$ \partial A=\{ (x,\pm1)\in\mathbb{R}^2: -1≦x≦1 \}\cup\{ (\pm1,y): -1≦y≦1 \} $$
$$ \overline{A}=\{ (x,y)\in\mathbb{R}^2: \ |x|≦1, \ |y|≦1 \}, \quad A^i=\{ (x,y)\in\mathbb{R}^2: \ |x|<1, \ |y|<1 \} $$
よって、 \( \overline{A}\not=A, \ A^i\not=A \) であるので、 \( A \) は閉集合でも開集合でもない。
(2) \( B=\{ (x,y)\in\mathbb{R}^2: x^2+y^2<1 \} \) とおく。このとき、
$$ \partial B=\{ (x,y)\in\mathbb{R}^2: x^2+y^2=1 \} $$
$$ \overline{B}=\{ (x,y)\in\mathbb{R}^2: x^2+y^2≦1 \}, \quad B^i=\{ (x,y)\in\mathbb{R}^2: x^2+y^2<1 \} $$
よって、 \( B^i=B \) であるので、 \( B \) は開集合である。
(3) \( C=\{ (x,y)\in\mathbb{R}^2: x+y≧1 \} \) とおく。このとき、
$$ \partial C=\{ (x,y)\in\mathbb{R}^2: x+y=1 \} $$
$$ \overline{C}=\{ (x,y)\in\mathbb{R}^2: x+y≧1 \}, \quad C^i=\{ (x,y)\in\mathbb{R}^2: x+y>1 \} $$
よって、 \( \overline{C}=C \) であるので、 \( C \) は閉集合である。
最後に、弧状連結という概念について紹介します。
集合 \( D \) 内の任意の2点 \( P,Q \) に対して、 \( P \) と \( Q \) が \( D \) から出ない曲線で結べるとき、 \( D \) を弧状連結という。
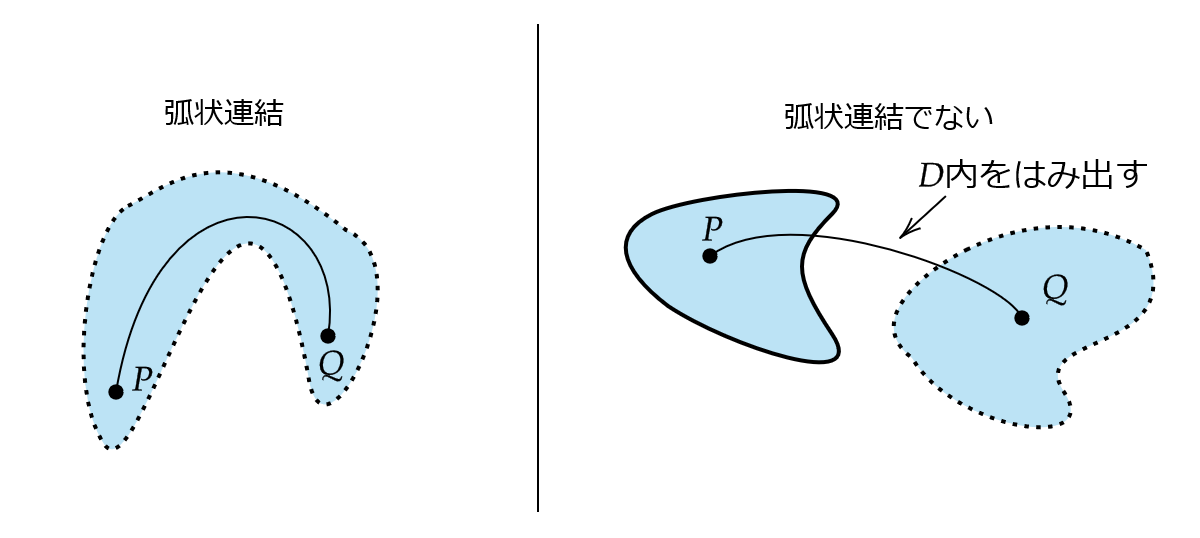
(1) 例2の3つの集合 \( A,B,C \) はすべて弧状連結である。
(2) \( D=\{ (x,y)\in\mathbb{R}^2: |y|>1 \} \) は弧状連結ではない。
実際、2点 \( (0,2), \ (0,-2) \) をとると、この2点を結ぶ曲線は \( D \) をはみ出す。
2変数関数の極限
それでは、2変数関数の極限について定義していきましょう。
\( (x,y) \) が \( (a,b) \) にどのように近づいたとしても、 \( f(x,y) \) が \( \ell \) に近づくとき、
$$ \lim_{(x,y)\to (a,b)}f(x,y)=\ell \quad \text{または} \quad f(x,y)\to \ell \ ((x,y)\to (a,b)) $$
と表す。このとき、 \( (x,y)\to (a,b) \) のとき \( f(x,y) \) は \( \ell \) に収束するという。
同様に、 \( (x,y) \) が \( (a,b) \) にどのように近づいたとしても、 \( f(x,y) \) が限りなく大きくなるとき、
$$ \lim_{(x,y)\to (a,b)}f(x,y)=\infty \quad \text{または} \quad f(x,y)\to \infty \ ((x,y)\to (a,b)) $$
と表す。このとき、 \( (x,y)\to (a,b) \) のとき \( f(x,y) \) は正の無限大に発散するという。
2変数関数の極限も1変数関数の極限と同様の性質が成り立ちます。まとめておきましょう。
関数 \( f(x,y),g(x,y) \) が収束して、 \( \displaystyle \lim_{(x,y)\to (a,b)}f(x,y)=\alpha, \ \lim_{(x,y)\to (a,b)}g(x,y)=\beta \) のとき、次が成り立つ。
(1) \( \displaystyle \lim_{(x,y)\to (a,b)}kf(x,y)=k\alpha \quad (k\text{は定数}) \)
(2) \( \displaystyle \lim_{(x,y)\to (a,b)}(f(x,y)+g(x,y))=\alpha+\beta \)
\( \displaystyle \lim_{(x,y)\to (a,b)}(f(x,y)-g(x,y))=\alpha-\beta \)
(3) \( \displaystyle \lim_{(x,y)\to (a,b)}f(x,y)g(x,y)=\alpha\beta \)
(4) \( \displaystyle \lim_{(x,y)\to (a,b)}\frac{f(x,y)}{g(x,y)}=\frac{\alpha}{\beta} \quad (\beta\not=0) \)
(1) 関数 \( f(x,y), \ g(x,y) \) が \( (a,b) \) の近くで \( f(x,y)≦ g(x,y) \) が成り立ち、
$$ \lim_{(x,y)\to (a,b)}f(x,y)=\alpha, \quad \lim_{(x,y)\to (a,b)}g(x,y)=\beta $$
ならば、 \( \alpha≦\beta \)
(2) (はさみうちの原理)
関数 \( f(x,y), \ g(x,y), \ h(x,y) \) が \( (a,b) \) の近くで \( f(x,y)≦ g(x,y)≦ h(x,y) \) が成り立ち、
$$ \lim_{(x,y)\to (a,b)}f(x,y)=\lim_{(x,y)\to (a,b)}h(x,y)=\alpha $$
ならば、 \( \displaystyle \lim_{(x,y)\to (a,b)}g(x,y)=\alpha \)
(1) \( (x,y)\not=(0,0) \) に対して、 \( f(x,y)=\frac{xy}{\sqrt{x^2+y^2}} \) とおく。
このとき、 \( \displaystyle \lim_{(x,y)\to(0,0)}\frac{xy}{\sqrt{x^2+y^2}} \) を求める。
$$ (x+y)^2≧0, \quad (x-y)^2≧0 $$
より、 \( 2|xy|≦x^2+y^2 \) が成り立つ。よって、
$$ |f(x,y)|=\frac{|xy|}{\sqrt{x^2+y^2}}≦\frac{\sqrt{x^2+y^2}}{2} $$
であり、 \( \displaystyle \lim_{(x,y)\to(0,0)}\frac{\sqrt{x^2+y^2}}{2}=0 \) より、はさみうちの原理より、
$$ \lim_{(x,y)\to(0,0)}\frac{xy}{\sqrt{x^2+y^2}}=0 $$
(2) \( (x,y)\not=(0,0) \) に対して、 \( f(x,y)=\frac{xy}{x^2+y^2} \) とおく。
このとき、 \( \displaystyle \lim_{(x,y)\to(0,0)}\frac{xy}{x^2+y^2} \) を求める。
\( x=r\cos \theta, \ y=r\sin \theta \) と極座標変換すると、
$$ \frac{xy}{x^2+y^2}=\frac{r\cos\theta \cdot r\sin\theta}{r^2\cos^2\theta+r^2\sin^2\theta}=\frac{r^2\cos\theta\sin\theta}{r^2}=\cos\theta\sin\theta $$
ここで、 \( (x,y)\to(0,0) \) とは \( \theta \) を固定して \( r\to+0 \) とすることとなる。
よって、 \( \theta \) を固定して \( r\to+0 \) すると、 \( \frac{xy}{x^2+y^2} \) は \( \cos\theta\sin\theta \) に近づいていく(正確には常に \( \cos\theta\sin\theta \) をとり続ける)が、これは \( \theta \) によって(つまり、 \( (x,y)\to(0,0) \) の近づけ方によって)値が変わってしまうため、 \( \displaystyle \lim_{(x,y)\to(0,0)}\frac{xy}{x^2+y^2} \) は存在しない。
(3) 次の関数の \( (x,y)\to(0,0) \) での極限を考える。
$$ f(x,y)=\begin{cases} y\sin \left( \frac{1}{x} \right) & (x\not=0 のとき) \\ 0 & (x=0のとき) \end{cases} $$
まず、 \( x\not=0 \) のとき、 \( |\sin x|≦1 \) より、
$$ |f(x,y)|=\left| y\sin \left( \frac{1}{x} \right) \right|=|y|\cdot \left|\sin \left( \frac{1}{x} \right) \right|≦|y| $$
また、 \( x=0 \) のとき、
$$ |f(x,y)|=0≦|y| $$
よって、すべての \( (x,y) \) に対して、 \( |f(x,y)|≦|y| \) であり、 \( \displaystyle \lim_{(x,y)\to(0,0)}|y|=0 \) なので、はさみうちの原理より、
$$ \lim_{(x,y)\to(0,0)}f(x,y)=0 $$
最後に、累次極限について考えましょう。
2変数関数 \( f(x,y) \) に対して、
$$ \lim_{y\to b}\left(\lim_{x\to a}f(x,y)\right), \quad \lim_{x\to a}\left(\lim_{y\to b}f(x,y) \right) $$
を累次極限という。
再び、次の関数を考える。
$$ f(x,y)=\begin{cases} y\sin \left( \frac{1}{x} \right) & (x\not=0 のとき) \\ 0 & (x=0のとき) \end{cases} $$
このとき、累次極限
$$ \lim_{y\to 0}\left(\lim_{x\to 0}f(x,y)\right), \quad \lim_{x\to 0}\left(\lim_{y\to 0}f(x,y) \right) $$
は等しくないことを示す。
まず、 \( \displaystyle \lim_{x\to 0}\left(\lim_{y\to 0}f(x,y)\right) \) を考える。
極限の定義より、 \( x\not=0 \) としたときの \( x\to 0 \) での \( \displaystyle \lim_{y\to 0}f(x,y) \) の近づき方を見ればよい。
$$ \lim_{y\to 0}f(x,y)=\lim_{y\to0}y\sin \left( \frac{1}{x} \right)=\sin \left(\frac{1}{x} \right)\lim_{y\to0}y=0 $$
よって、
$$ \lim_{x\to 0}\left(\lim_{y\to 0}f(x,y)\right)=\lim_{x\to0}0=0 $$
次に、 \( \displaystyle \lim_{y\to 0}\left(\lim_{x\to 0}f(x,y)\right) \) を考える。
極限の定義より、 \( y\not=0 \) としたときの \( y\to 0 \) での \( \displaystyle \lim_{x\to 0}f(x,y) \) の近づき方を見ればよい。
また、 \( \displaystyle \lim_{x\to 0}f(x,y) \) の方も極限の定義より、 \( x\not=0 \) としたときの \( x\to 0 \) での \( f(x,y) \) の近づき方を見ればよい。
このとき、
$$ \lim_{x\to0}f(x,y)=\lim_{x\to0}y\sin \left( \frac{1}{x} \right)=y\lim_{x\to0}\sin \left( \frac{1}{x} \right) \quad (y\not=0) $$
ここで、 \( \displaystyle \lim_{x\to0}\sin \left( \frac{1}{x} \right) \) は振動してしまうので、極限 \( \displaystyle \lim_{x\to0}f(x,y) \) は存在しない。
したがって、 \( \displaystyle \lim_{y\to 0}\left(\lim_{x\to 0}f(x,y)\right) \) も存在しない。
2変数関数の極限と累次極限との関係について次が成り立ちます。
\( \displaystyle \lim_{(x,y)\to (a,b)}f(x,y)=\alpha \) が存在するとき、2つの累次極限
$$ \lim_{x\to a}\left\{ \lim_{y\to b}f(x,y) \right\}, \quad \lim_{y\to b}\left\{ \lim_{x\to a}f(x,y) \right\} $$
は存在して、ともに \( \alpha \) に等しい。ただし、 \( \{ \ \} \) 内の極限は存在するものとする。
2変数関数の連続性
1変数関数と同様にして、次のように2変数関数の連続性を定めます。
関数 \( f(x,y) \) が定義域 \( D \) 上の点 \( (a,b) \) で
$$ \lim_{(x,y)\to(a,b)}f(x,y)=f(a,b) $$
が成り立つとき、 \( f \) は点 \( (a,b) \) で連続であるという。
また、すべての \( (a,b)\in D \) で \( f \) が連続であるとき、 \( f \) は \( D \) 上連続であるという。
連続性に関しても1変数関数と同様の性質が成り立ちます。
\( f,g \) を \( D \) 上連続な関数として、 \( (a,b)\in D, \ k,\ell \) を実数とする。
(1) \( kf(x,y)+\ell g(x,y) \) も \( D \) 上連続であり、次が成り立つ。
$$ \lim_{(x,y)\to (a,b)}(kf(x,y)+\ell g(x,y))=kf(a,b)+\ell g(a,b) $$
(2) \( f(x,y)g(x,y) \) も \( D \) 上連続であり、次が成り立つ。
$$ \lim_{(x,y)\to (a,b)}f(x,y)g(x,y)=f(a,b)g(a,b) $$
(3) すべての \( (x,y)\in D \) に対して、 \( g(x,y)\not=0 \) のとき、 \( \frac{f(x,y)}{g(x,y)} \) も \( D \) 上連続であり、次が成り立つ。
$$ \lim_{(x,y)\to (a,b)}\frac{f(x,y)}{g(x,y)}=\frac{f(a,b)}{g(a,b)} $$
(1) \( f \) を定義域 \( D \) 上の連続関数、 \( g \) を定義域 \( D’ \) 上の連続関数とする。
また、\( f,g \) を合成可能な関数(つまり \( f \) の値域を \( f(D) \) とおくと、 \( f(D)\subset D’ \))とする。
このとき、合成関数 \( (g\circ f)(x,y) \) も \( D \) 上連続であり、次が成り立つ。
$$ \lim_{(x,y)\to (a,b)}g\circ f(x,y)=g\circ f(a,b) $$
(2) 有界閉集合上で連続な関数は、その集合上で最大値・最小値をもつ。
関数 \( f(x,y) \) が弧状連結な集合 \( D \) 上定義された連続関数で
$$ f(a,b)\not=f(c,d) \quad ((a,b),(c,d)\in D) $$
ならば、 \( f(a,b) \) と \( f(c,d) \) の間の任意の値 \( m \) に対して、
$$ f(x_0,y_0)=m $$
となる \( (x_0,y_0)\in D \) が少なくとも1つ存在する。
(1) 次の関数を考える。
$$ f(x,y)= \begin{cases} \frac{xy(x^2+y^2)}{3x^2+y^2} & ((x,y)\not=0のとき) \\ 0 & ((x,y)=(0,0)のとき) \end{cases} $$
この関数は \( (x,y)\in \mathbb{R}^2 \) 上連続であることを示す。
\( (x,y)\not=0 \) のときは、定理5を何回か用いることにより \( (x,y) \) 上の連続性が示せる。
よって、 \( (x,y)=(0,0) \) 上の連続性を調べればよい。
極限の定義より、 \( (x,y)\not=0 \) としたときの \( (x,y)\to (0,0) \) での \( f(x,y) \) の近づき方を見ればよい。
よって、 \( (x,y)\not=0 \) のとき、
$$ |f(x,y)|=\left|\frac{xy(x^2+y^2)}{3x^2+y^2}\right|≦\left|\frac{xy(x^2+y^2)}{x^2+y^2}\right|=|xy| $$
であり、 \( \displaystyle \lim_{(x,y)\to(0,0)}|xy|=0 \) なので、はさみうちの原理より、
$$ \lim_{(x,y)\to(0,0)}f(x,y)=0=f(0,0) $$
よって、 \( (x,y)=(0,0) \) 上でも連続である。
(2) 次の関数を考える。
$$ f(x,y)=\begin{cases} \frac{x^5}{(y-x^2)^2+x^6} & ((x,y)\not=(0,0) のとき) \\ 0 & ((x,y)=(0,0) のとき) \end{cases} $$
この関数は原点 \( (0,0) \) で不連続であることを示す。
実際、 \( (x,y)\to (0,0) \) の近づけ方として、 \( y=x^2 \) に沿って \( (x,y)\to (0,0) \) とすることを考えると、
$$ \begin{align} f(x,y)&=f(x,x^2)=\frac{x^5}{(x^2-x^2)^2+x^6} \\ &=\frac{x^5}{x^6}=\frac{1}{x}\not\to f(0,0) \quad ((x,y)\to(0,0)) \end{align} $$
よって、 \( \displaystyle \lim_{(x,y)\to(0,0)}f(x,y) \) は存在しないので、原点 \( (0,0) \) で不連続である。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

