こんにちは、ひかりです。
今回は微分積分学から1変数関数の積分について解説していきます。
この記事では以下のことを紹介します。
- 1変数関数の積分の定義とその性質について
- 置換積分法・部分積分法と基本的な関数の積分について
- 有理関数・三角関数・無理関数を含む積分の計算方法について
1変数関数の積分の定義と性質
積分の定義と性質
高校数学では、積分というのは微分の逆操作であると定義しました。
ここでは、積分のきちんとした定義を述べて、微分との関係性を見ていきましょう。
考え方としては、高校数学で学んだ区分求積法に近いです。
関数 \( f(x) \) が区間 \( [a,b] \) で連続とします。
(本当は連続である必要はないですが、話を簡単にするため連続とします)
このとき、区間 \( [a,b] \) を細かく \( n \) 個に分割していきます。
その分割を
$$ 分割 \ \Delta: \ a=x_0<x_1<\cdots<x_n=b $$
と表します。また、次の記号を定めます。
$$ |\Delta|=\max \{ x_i-x_{i-1}|i=1,2,\cdots,n \} $$
$$ I_i=[x_{i-1},x_i], \quad |I_i|=x_i-x_{i-1} $$
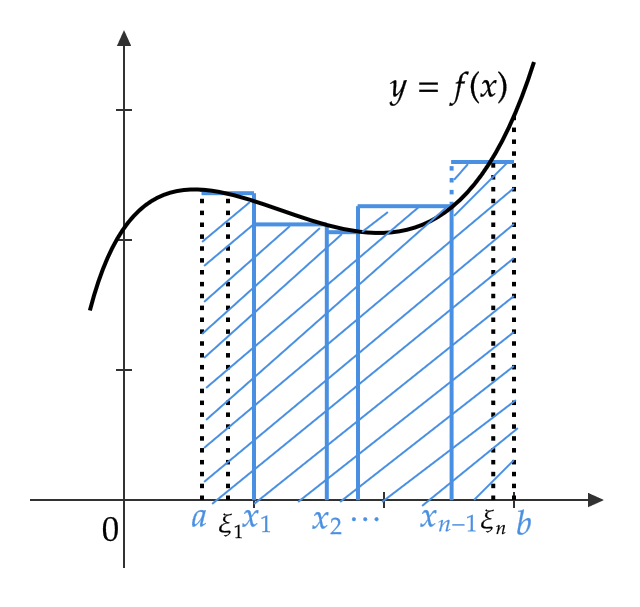
このとき、 \( \xi_i\in I_i \) を選んだときの \( f \) のリーマン和 \( R[\{\xi_i\},\Delta,f] \) を次で定めます。
$$ R[\{\xi_i\},\Delta,f]=\sum_{i=1}^nf(\xi_i)|I_i| $$
(つまり、分割によってできた各長方形の面積の和をリーマン和とよんでいます)
区分求積法との違いは細分の仕方が等分である必要がないことと、長方形の縦の長さを決める点を右端に限らず細分区間内のどこの点でもかまわないというところになります。
このリーマン和を用いて、次のように(リーマン)積分を定義します。
\( |\Delta|\to 0 \) のとき、 \( \xi_i \) の選び方によらない数 \( S \) が存在して、
$$ \lim_{|\Delta|\to0}R[\{\xi_i\},\Delta,f]=S $$
となるとき、 \( f \) は \( I \) 上(リーマン)積分可能という。
(これは区間の分割をどんどん細分化していくことに相当します)
また、このとき \( S \) を
$$ \int_a^bf(x)dx $$
とかいて、 \( f \) の \( I \) 上での定積分という。
また、 \( b<a \) の場合の積分を次のように定めます。
\( f \) を \( I=[b,a] \ (b<a) \) 上積分可能とする。このとき、
$$ \int_a^bf(x)dx=-\int_b^af(x)dx $$
と定める。また、
$$ \int_a^af(x)=0 $$
と定める。
(1) 区間 \( [a,b] \) で \( f(x)=c \ (c:定数) \) であるとき、 \( \displaystyle \int_a^bf(x)dx \) を定義にしたがって求める。
$$ R[\{\xi_i\},\Delta,f]=\sum_{i=1}^nf(\xi_i)|I_i|=\sum_{i=1}^nc(x_i-x_{i-1})=c\sum_{i=1}^n(x_i-x_{i-1})=c(b-a) $$
よって、
$$ \int_a^bf(x)dx=\lim_{|\Delta|\to0}R[\{\xi_i\},\Delta,f]=c(b-a) $$
(2) \( \displaystyle \int_0^bx^2dx \) を定義にしたがって求める。
分割
$$ \Delta: \ 0=x_0<x_1<\cdots<x_n=b $$
を与えたとき、
$$ 3x_{i-1}^2<x_i^2+x_ix_{i-1}+x_{i-1}^2<3x_i^2 $$
であるので、中間値の定理より、
$$ 3\xi_i^2=x_i^2+x_ix_{i-1}+x_{i-1}^2, \quad (x_{i-1}<\xi_i<x_i) $$
をみたす \( \xi_i \) が存在する。
$$ 3\xi_i^2(x_i-x_{i-1})=(x_i^2+x_ix_{i-1}+x_{i-1}^2)(x_i-x_{i-1})=x_i^3-x_{i-1}^3 $$
であるので、
$$ 3\sum_{i=1}^n\xi_i^2(x_i-x_{i-1})=\sum_{i=1}^n(x_i^3-x_{i-1}^3)=b^3 $$
したがって、
$$ \int_0^bx^2dx=\lim_{|\Delta|\to0}R[\{\xi_i\},\Delta,f]=\lim_{|\Delta|\to0}\sum_{i=1}^n\xi_i^2(x_i-x_{i-1})=\frac{b^3}{3} $$
この例のように、定義にしたがって積分を求めるのは非常に大変です。
よって、もう少し積分について見ていきましょう。
そのために、高校数学で学んだ定積分の性質を振り返りをします。
\( f, \ g \) を \( I=[a,b] \) 上積分可能とする。
(1) $$ \int_a^bkf(x)dx=k\int_a^bf(x)dx \quad (k:定数) $$
(2) $$ \int_a^b\{ f(x)+g(x) \} dx=\int_a^bf(x)dx+\int_a^bg(x)dx $$
(3) $$ \int_a^b\{ f(x)-g(x) \} dx=\int_a^bf(x)dx-\int_a^bg(x)dx $$
(4) $$ \int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx $$
また、次のような性質も成り立ちます。
\( f, \ g \) を \( I=[a,b] \) 上積分可能とする。
(1) すべての \( x\in I \) に対して、 \( f(x)≧0 \) であるとき、次が成り立つ。
$$ \int_a^bf(x)dx≧0 $$
(2) すべての \( x\in I \) に対して、 \( f(x)≧g(x) \) であるとき、次が成り立つ。
$$ \int_a^bf(x)dx≧\int_a^bg(x)dx $$
(3) \( |f| \) も \( I=[a,b] \) 上積分可能であり、次が成り立つ。
$$ \int_a^b|f(x)|dx≧\left| \int_a^bf(x)dx \right| $$
最後に積分可能性の条件を1つ紹介します。
関数 \( f \) が \( I=[a,b] \) 上で連続であるとき、 \( f \) は \( I \) 上で積分可能である。
微分と積分の関係(微積分学の基本定理)
ここでは、積分をリーマン和によって定義しています。よって、微分との関係性はいまのところわかりません。
そこで、微分と積分を関連付ける重要な定理である微積分学の基本定理を紹介します。
(1) \( f \) を \( I=[a,b] \) 上連続であるとして、 \( c\in I \) とする。
そして、関数 \( F(x) \) を次のように定めます。
$$ F(x)=\int_c^xf(t)dt $$
このとき、 \( F \) は \( I \) 上微分可能であり、
$$ F'(x)=f(x) $$
となる。
このように、 \( F'(x)=f(x) \) となる \( F \) のことを \( f \) の原始関数という。
(2) \( f \) を \( I=[a,b] \) 上連続であるとして、 \( f \) の原始関数を \( F \) とする。このとき、
$$ \int_a^bf(t)dt=F(b)-F(a) $$
証明には次の積分に関する平均値の定理を用います。
\( f \) が \( I=[a,b] \) 上で連続であるとする。このとき、
$$ \int_a^bf(x)dx=f(\xi)(b-a) $$
をみたす \( \xi\in I \) が存在する。
定理5の証明(気になる方だけクリックしてください)
微分積分学03の記事の定理5より、連続関数 \( f \) は \( I \) 上で最大値・最小値をもちます。
つまり、その最大値を \( M \) 、最小値 \( m \) とおくと、
$$ m≦f(x)≦M $$
定理2の(2)より、
$$ \int_a^bmdx≦\int_a^bf(x)dx≦\int_a^bMdx $$
例1の(1)より、
$$ m(b-a)≦\int_a^bf(x)dx≦M(b-a) $$
したがって、 \( (b-a) \) で割ると
$$ m≦\frac{1}{b-a}\int_a^bf(x)dx≦M $$
となるので、中間値の定理より、
$$ f(\xi)=\frac{1}{b-a}\int_a^bf(x)dx $$
をみたす \( \xi\in[a,b] \) が存在します。
よって、定理が成り立ちます。
定理4の証明(気になる方だけクリックしてください)
(1) \( x\in I \) に対して、 \( x+h \in I \) となるように0でない実数 \( h \) を十分小さくとります。すると、
$$ F(x+h)-F(x)=\int_c^{x+h}f(t)dt-\int_c^xf(t)dt=\int_x^{x+h}f(t)dt $$
最右辺は定理5を用いると、
$$ \int_x^{x+h}f(t)dt=hf(\xi_h) $$
となる \( \xi_h \) が \( x \) と \( x+h \) の間に存在します。
( \( h<0 \) のときは \( \displaystyle \int_x^{x+h}f(t)dt=-\int_{x-|h|}^xf(t)dt \) とすればよい)
したがって、
$$ \frac{F(x+h)-F(x)}{h}=f(\xi_h) $$
ここで、 \( h\to 0 \) のとき \( \xi_h\to x \) であるので、 \( f(x) \) の連続性より、
$$ F'(x)=\lim_{h\to0}\frac{F(x+h)-F(x)}{h}=\lim_{h\to0}f(\xi_h)=f(x) $$
よって、(1)が示せました。
(2) (1)より \( \displaystyle \int_a^x f(t)dt \) は \( f \) の原始関数であるので、
$$ F(x)=\int_a^xf(t)dt+C $$
となる定数 \( C \) が存在します。
(高校数学(数学Ⅲ)11の記事のはじめの議論より、2つの原始関数があったらそれらの原始関数は定数差しかありません)
よって、
$$ F(b)-F(a)=\left( \int_a^bf(t)dt+C\right)-\left( \int_a^af(t)dt+C\right)=\int_a^bf(t)dt $$
これで、(2)も示せました。
最後に不定積分を定義してこの節を終わりにしたいと思います。
ある区間 \( I \) で定義された関数 \( f(x) \) の原始関数を \( \displaystyle \int f(x)dx \) と表し、 \( f(x) \) の不定積分という。
置換積分法・部分積分法と基本的な関数の積分
置換積分法と部分積分法
置換積分法と部分積分法を振り返っていきましょう。
詳しく知りたい方は以下の記事をご覧ください。
\( g(x) \) が微分可能であり、\( f(x) \)と \( g'(x) \) が連続ならば、次が成り立つ。
$$ \int f(x)dx=\int f(g(t))g'(t)dt $$
$$ \int_a^bf(x)dx=\int_{\alpha}^{\beta} f(g(t))g'(t)dt $$
ここで、 \( a=g(\alpha), \ b=g(\beta) \) である。
\( f(x), \ g(x) \) が \( C^1 \) 級(微分可能でその導関数が連続)であるならば、次が成り立つ。
$$ \int f(x)g'(x)dx=f(x)g(x)-\int f'(x)g(x)dx $$
$$ \int_a^b f(x)g'(x)dx=[f(x)g(x)]^b_a-\int_a^b f'(x)g(x)dx $$
基本的な関数の積分
置換積分法や部分積分法を駆使することにより、さまざまな関数の原始関数を求めることができます。
それらを下の表にまとめましたのでご覧ください。
表の後の例にて、いくつかの関数の原始関数を実際に求めています。
| \( f(x) \) | \( \displaystyle \int f(x)dx \) |
| \( x^k \ (k\not=-1) \) | \( \frac{x^{k+1}}{k+1} \) |
| \( x^{-1} \) | \( \log|x| \) |
| \( e^x \) | \( e^x \) |
| \( a^x \ (a>0, \ a\not=1) \) | \( \frac{a^x}{\log a} \) |
| \( \log x \) | \( x\log x-x \) |
| \( \sin x \) | \( -\cos x \) |
| \( \cos x \) | \( \sin x \) |
| \( \tan x \) | \( -\log|\cos x| \) |
| \( \sin^{-1} x \) | \( x\sin^{-1} x+\sqrt{1-x^2} \) |
| \( \cos^{-1} x \) | \( x\cos^{-1} x-\sqrt{1-x^2} \) |
| \( \tan^{-1} x \) | \( x\tan^{-1} x-\frac{1}{2}\log(1+x^2) \) |
| \( \sinh x \) | \( \cosh x \) |
| \( \cosh x \) | \( \sinh x \) |
| \( \tanh x \) | \( \log|\cosh x| \) |
| \( \frac{1}{x^2-a^2} \ (a\not=0) \) | \( \frac{1}{2a}\log \left|\frac{x-a}{x+a} \right| \) |
| \( \frac{1}{x^2+a^2} \ (a\not=0) \) | \( \frac{1}{a}\tan^{-1}\frac{x}{a} \) |
| \( \frac{1}{\sqrt{a^2-x^2}} \ (a\not=0) \) | \( \sin^{-1}\frac{x}{a} \) |
| \( \sqrt{a^2-x^2} \ (a\not=0) \) | \( \frac{1}{2}\left( x\sqrt{a^2-x^2}+a^2\sin^{-1}\frac{x}{a} \right) \) |
| \( \frac{1}{\sqrt{x^2+a}} \ (a\not=0) \) | \( \log|x+\sqrt{x^2+a}| \) |
| \( \sqrt{x^2+a} \ (a\not=0) \) | \( \frac{1}{2}\left( x\sqrt{x^2+a}+a\log|x+\sqrt{x^2+a}| \right) \) |
(1) \( \sin^{-1}x \) の原始関数を求める。
$$ (\sin^{-1}x)’=\frac{1}{\sqrt{1-x^2}} $$
であるので、部分積分を用いると、
$$ \int \sin^{-1}xdx=\int (x)’\sin^{-1}xdx=x\sin^{-1}x-\int \frac{x}{\sqrt{1-x^2}}dx $$
ここで、
$$ (\sqrt{1-x^2})’=\frac{-2x}{2\sqrt{1-x^2}}=-\frac{x}{\sqrt{1-x^2}} $$
であるので、
$$ \int \sin^{-1}xdx=x\sin^{-1}x+\sqrt{1-x^2} $$
(2) \( \sqrt{x^2+a} \ (a\not=0) \) の原始関数を求める。
\( \displaystyle I=\int \sqrt{x^2+a}dx \) とおいて、部分積分を用いると、
$$ \begin{align} I=\int \sqrt{x^2+a}dx&=\int (x)’\sqrt{x^2+a}dx=x\sqrt{x^2+a}-\int x\frac{2x}{2\sqrt{x^2+a}}dx \\ &=x\sqrt{x^2+a}-\int \frac{x^2}{\sqrt{x^2+a}}dx \\ &=x\sqrt{x^2+a}-\int \frac{(x^2+a)-a}{\sqrt{x^2+a}}dx \\ &=x\sqrt{x^2+a}-\int \left( \sqrt{x^2+a}-\frac{a}{\sqrt{x^2+a}} \right) dx \\ &=x\sqrt{x^2+a}-\int \sqrt{x^2+a}dx+a\int \frac{1}{\sqrt{x^2+a}}dx \\ &=x\sqrt{x^2+a}-I+a\int \frac{1}{\sqrt{x^2+a}}dx \end{align} $$
よって、 \( I \) でまとめると、
$$ I=\frac{1}{2} \left( x\sqrt{x^2+a}+a\int \frac{1}{\sqrt{x^2+a}}dx\right) $$
\( \displaystyle \int \frac{1}{\sqrt{x^2+a}}dx \) を置換積分で求める。
\( \sqrt{x^2+a}=t-x \) とおくと、
$$ x^2+a=t^2-2tx+x^2 $$
より、 \( x=\frac{t^2-a}{2t} \) となる。また、
$$ dx=\frac{d}{dt}\left( \frac{t^2-a}{2t} \right) dt=\frac{4t^2-2(t^2-a)}{4t^2}dt=\frac{t^2+a}{2t^2}dt $$
よって、
$$ \begin{align} \int \frac{1}{\sqrt{x^2+a}}dx&=\int \frac{1}{t-\frac{t^2-a}{2t}}\cdot \frac{t^2+a}{2t^2}dt \\ &=\int \frac{2t}{2t^2-(t^2-a)}\cdot \frac{t^2+a}{2t^2}dt=\int \frac{2t}{t^2+a}\cdot\frac{t^2+a}{2t^2}dt \\ &=\int \frac{1}{t}dt=\log|t|=\log|x+\sqrt{x^2+a}| \end{align} $$
したがって、いままでの計算をまとめると、
$$ \begin{align} \int \sqrt{x^2+a}dx&=\frac{1}{2} \left( x\sqrt{x^2+a}+a\int \frac{1}{\sqrt{x^2+a}}dx\right) \\ &=\frac{1}{2} \left( x\sqrt{x^2+a}+a\log|x+\sqrt{x^2+a}| \right) \end{align} $$
有理関数・三角関数・無理関数を含む積分の計算方法
先ほどの例2の(2)で \( \sqrt{x^2+a}=t-x \) とおいていますが、このような置き方をどうして思いつくのでしょうか。
実は、こういう形の関数の積分にはこういう計算方法で原始関数を求めることができるというような、ある程度の指針があります。
その指針について紹介していきます。
有理関数を含む積分の計算方法
\( \frac{x^2+x+1}{x^3+3x} \) のように、多項式の分数の形で表される関数のことを有理関数といいます。
これは一般に多項式 \( P(x), \ Q(x) \) を用いて \( f(x)=\frac{Q(x)}{P(x)} \) と表せます。
ただし、 \( P(x) \) の最高次の係数は1であるとします。
もし、最高次の係数が1でないときは分母分子をその係数で割ることで1にします。
(例えば \( f(x)=\frac{x^2+2}{2x^3+x^2+1} \) であるときは、分母分子を2で割って、 \( f(x)=\frac{\frac{1}{2}x^2+1}{x^3+\frac{1}{2}x^2+\frac{1}{2}} \) とします)
(1) まず、 \( Q(x)の次数≧P(x)の次数 \) であるときを考えます。
このときは、 \( Q(x) \) 割る \( P(x) \) の商を \( S(x) \) 、余りを \( R(x) \) とおくと、次のように表せます。
$$ Q(x)=P(x)S(x)+R(x) $$
( \( 11\div 5 \) を \( 11=5\times 2+1 \) と表すのと同じです)
すると、
$$ \frac{Q(x)}{P(x)}=\frac{P(x)S(x)+R(x)}{P(x)}=S(x)+\frac{R(x)}{P(x)} $$
このとき、 \( R(x) \) は多項式の割り算の余りなので \( \frac{R(x)}{P(x)} \) は \( R(x)の次数<P(x)の次数 \) となります。
また、 \( S(x) \) は多項式なので、簡単に積分できます。
よって、有理関数はこの方法で次数を下げることにより、すべて次の \( Q(x)の次数<P(x)の次数 \) であるときに帰着することができます。
(2) \( Q(x)の次数<P(x)の次数 \) であるときを考えます。
まず、 \( P(x) \) を実数の範囲で因数分解をします。
すると、 \( P(x) \) は次のように相異なる1次式と実解をもたない2次式の形に分解することができます。
$$ P(x)=(x+\alpha_1)^{m_1}(x+\alpha_2)^{m_2}\cdots (x^2+\beta_1x+\gamma_1)^{n_1}(x^2+\beta_2x+\gamma_2)^{n_2}\cdots $$
ここで、係数はすべて実数で、 \( \beta_i^2-4\gamma_i<0 \) (判別式が負) です。
簡単にするために、ここでは \( P(x)=(x+a)^n(x+b)^m(x^2+cx+d)^{\ell} \) とします。
すると、 \( \frac{Q(x)}{P(x)} \) は次のように分解することができます。(これを部分分数分解といいます)
$$ \begin{align} \frac{Q(x)}{P(x)}&=\frac{A_1}{x+a}+\frac{A_2}{(x+a)^2}+\cdots+\frac{A_n}{(x+a)^n} \\ &\quad +\frac{B_1}{x+b}+\frac{B_2}{(x+b)^2}+\cdots+\frac{B_m}{(x+b)^m} \\ &\quad +\frac{C_1x+D_1}{x^2+cx+d}+\frac{C_2x+D_2}{(x^2+cx+d)^2}+\cdots+\frac{C_{\ell}x+D_{\ell}}{(x^2+cx+d)^{\ell}} \end{align} $$
そして、各項の有理関数の積分を求めればよい。
$$ \int \frac{A}{x+a}dx=A\log|x+a| $$
$$ \int \frac{A}{(x+a)^n}dx=-\frac{A}{(n-1)(x+a)^{n-1}} \quad (n≧2) $$
$$ \begin{align} &\int \frac{Bx+C}{x^2+bx+c}dx=\int \frac{\frac{B}{2}(2x+b)+\left( C-\frac{Bb}{2} \right)}{x^2+bx+c}dx \\ &=\frac{B}{2}\int \frac{2x+b}{x^2+bx+c}dx+\left( C-\frac{Bb}{2} \right)\int \frac{1}{x^2+bx+c}dx \\ &=\frac{B}{2}\int \frac{(x^2+bx+c)’}{x^2+bx+c}dx+\left( C-\frac{Bb}{2} \right)\int \frac{1}{\left( x+\frac{b}{2}\right)^2+\left( c-\frac{b^2}{4} \right)} dx \\ &=\frac{B}{2}\log|x^2+bx+c|+\left( C-\frac{Bb}{2}\right)\cdot \frac{1}{\sqrt{c-\frac{b^2}{4}}}\tan^{-1}\left( \frac{x+\frac{b}{2}}{\sqrt{c-\frac{b^2}{4}}} \right) \end{align} $$
最後の式は先ほどの表の中の \( \displaystyle \int\frac{1}{y^2+\alpha^2}dy=\frac{1}{\alpha}\tan^{-1}\frac{y}{\alpha} \) を \( y=x+\frac{b}{2} \) と \( \alpha^2=c-\frac{b^2}{4} \) で用いています。
\( \displaystyle \int \frac{Bx+C}{(x^2+bx+c)^n}dx \) については、漸化式を用いて \( \displaystyle \int \frac{Bx+C}{x^2+bx+c}dx \) に帰着させることができますが、ここでは省略します。
まとめると、次のようになります。
有理関数 \( f(x)=\frac{Q(x)}{P(x)} \) の原始関数は次のようにして求めることができます。
(1) \( Q(x)の次数≧P(x)の次数 \) の場合は、 \( Q(x) \) 割る \( P(x) \) を計算して分子の次数を下げる。
(2) \( Q(x)の次数<P(x)の次数 \) の場合は、 \( \frac{Q(x)}{P(x)} \) を部分分数分解することにより、次の4つの積分の和で表すことができます。
$$ \int \frac{A}{x+a}dx, \quad \int \frac{A}{(x+a)^n}dx, \quad \int \frac{Bx+C}{x^2+bx+c}dx, \quad \int \frac{Bx+C}{(x^2+bx+c)^n}dx $$
これらは上のようにして計算することができる。
(1) \( \displaystyle \int \frac{1}{x^2-a^2}dx \ (a\not=0) \) を求める。
\( \frac{1}{x^2-a^2} \) を部分分数分解すると、
$$ \frac{1}{x^2-a^2}=\frac{1}{(x+a)(x-a)}=\frac{1}{2a}\left( \frac{1}{x-a}-\frac{1}{x+a} \right) $$
よって、
$$ \int \frac{1}{x^2-a^2}dx=\frac{1}{2a}\int \left( \frac{1}{x-a}-\frac{1}{x+a} \right)dx=\frac{1}{2a}\log \left| \frac{x-a}{x+a} \right| $$
(2) \( \displaystyle \int\frac{x^3-3x^2-2x}{x^2-4x+3}dx \) を求める。
\( \frac{x^3-3x^2-2x}{x^2-4x+3} \) の次数を下げると、
$$ \frac{x^3-3x^2-2x}{x^2-4x+3}=x+1-\frac{x+3}{x^2-4x+3}=x+1-\frac{x+3}{(x-1)(x-3)} $$
ここで、 \( \frac{x+3}{(x-1)(x-3)} \) を部分分数分解すると、
$$ \frac{x+3}{(x-1)(x-3)}=\frac{-2}{x-1}+\frac{3}{x-3} $$
よって、
$$ \begin{align} \int\frac{x^3-3x^2-2x}{x^2-4x+3}dx&=\int \left( x+1+\frac{2}{x-1}-\frac{3}{x-3} \right) dx \\ &=\frac{1}{2}x^2+x+2\log |x-1|-3\log|x-3| \\ &=\frac{1}{2}x^2+x+\log\frac{(x-1)^2}{|x-3|^3} \end{align} $$
三角関数を含む積分の計算方法
三角関数を含むような関数の積分についても、次のような解き方の指針があります。
(1) \( f(\cos x)\sin x \) という形の場合は、 \( t=\cos x \) とおいて置換積分する。すると、
$$ \int f(\cos x)\sin xdx=\int f(t)\sqrt{1-t^2}\frac{-1}{\sqrt{1-t^2}}dt=-\int f(t)dt $$
(2) \( f(\sin x)\cos x \) という形の場合は、 \( t=\sin x \) とおいて置換積分する。すると、
$$ \int f(\sin x)\cos xdx=\int f(t)\sqrt{1-t^2}\frac{1}{\sqrt{1-t^2}}dt=\int f(t)dt $$
(3) \( f(\cos x,\sin x) \) という形の場合は、 \( t=\tan \frac{x}{2} \) とおいて置換積分する。すると、
$$ \int f(\cos x,\sin x)dx=\int f\left( \frac{1-t^2}{1+t^2},\frac{2t}{1+t^2} \right) \frac{2}{1+t^2}dt $$
(4) \( f(\cos^2x,\sin^2x) \) という形の場合は、 \( t=\tan x \) とおいて置換積分する。すると、
$$ \int f(\cos^2 x,\sin^2 x)dx=\int f\left( \frac{1}{1+t^2},\frac{t^2}{1+t^2} \right) \frac{1}{1+t^2}dt $$
(5) \( \cos^nx, \ \sin^nx \) は、 \( n \) が奇数か偶数かで次のように解く。
\( n \) が奇数:次のようにして、(1),(2)に帰着させる。
$$ \cos^{2k+1}x=(\cos^2x)^k\cos x=(1-\sin^2x)^k\cos x=f(\sin x)\cos x $$
$$ \sin^{2k+1}x=(\sin^2x)^k\sin x=(1-\cos^2x)^k\sin x=f(\cos x)\sin x $$
\( n \) が偶数:半角の公式を用いて奇数になるまで次数を下げる。
$$ \cos^{2k}x=(\cos^2x)^k=\left( \frac{1+\cos 2x}{2} \right)^k $$
$$ \sin^{2k}x=(\sin^2x)^k=\left( \frac{1-\cos 2x}{2} \right)^k $$
定理9の証明(気になる方だけクリックしてください)
(3)を示します。
(3) \( t=\tan \frac{x}{2} \) とおくと、
$$ 1+t^2=1+\left( \tan \frac{x}{2} \right)^2=\frac{1}{\cos^2\frac{x}{2}} $$
よって、 \( \frac{1}{1+t^2}=\cos^2\frac{x}{2} \) であるので、倍角の公式を用いると、
$$ \cos x=\cos 2\cdot\frac{x}{2}=2\cos^2\frac{x}{2}-1=\frac{2}{1+t^2}-1=\frac{2-(1+t^2)}{1+t^2}=\frac{1-t^2}{1+t^2} $$
$$ \sin x=\sin 2\cdot\frac{x}{2}=2\sin\frac{x}{2}\cos \frac{x}{2}=2\frac{\sin\frac{x}{2}}{\cos\frac{x}{2}}\cos^2\frac{x}{2}=2\tan\frac{x}{2}\cos^2\frac{x}{2}=\frac{2t}{1+t^2} $$
また、 \( t=\tan\frac{x}{2} \) を \( x \) で微分すると、
$$ dt=\left( \tan\frac{x}{2} \right)’dx=\frac{1}{2}\frac{1}{\cos^2\frac{x}{2}}dx=\frac{1}{2}\left( 1+\tan^2\frac{x}{2}\right)dx=\frac{1+t^2}{2}dx $$
よって、 \( dx=\frac{2}{1+t^2}dt \) であるので、
$$ \int f(\cos x,\sin x)dx=\int f\left( \frac{1-t^2}{1+t^2},\frac{2t}{1+t^2} \right) \frac{2}{1+t^2}dt $$
(1) \( \displaystyle \int\frac{1}{\sin x}dx \) を求める。
\( t=\tan\frac{x}{2} \) とおくと、
$$ \sin x=\frac{2t}{1+t^2}, \quad dx=\frac{2}{1+t^2}dt $$
よって、
$$ \int\frac{1}{\sin x}dx=\int \frac{1+t^2}{2t}\cdot \frac{2}{1+t^2}dt=\int \frac{1}{t}dt=\log|t|=\log\left|\tan\frac{x}{2}\right| $$
(2) \( \displaystyle \int \cos^4x dx \) を求める。
半角の公式を用いて次数を下げる。
$$ \begin{align} \cos^4 x&=(\cos^2x)^2=\left( \frac{1+\cos 2x}{2} \right)^2=\frac{1}{4}+\frac{1}{2}\cos 2x+\frac{1}{4}\cos^2 2x \\ &=\frac{1}{4}+\frac{1}{2}\cos 2x+\frac{1}{4}\cdot\frac{1+\cos 4x}{2}=\frac{3}{8}+\frac{1}{2}\cos 2x+\frac{1}{8}\cos 4x \end{align} $$
よって、
$$ \begin{align} \int \cos^4xdx&=\int \left(\frac{3}{8}+\frac{1}{2}\cos 2x+\frac{1}{8}\cos 4x\right) dx \\ &=\frac{3}{8}x+\frac{1}{4}\sin 2x+\frac{1}{32}\sin 4x \end{align} $$
無理関数を含む積分の計算方法
無理関数を含むような関数の積分についても、次のような解き方の指針があります。
(1) \( f(x, \ \sqrt[n]{ax+b}) \) という形の場合は、 \( t=\sqrt[n]{ax+b} \) とおいて置換積分する。
(2) \( \displaystyle f\left( x, \ \sqrt[n]{\frac{ax+b}{cx+d}} \right) \) という形の場合は、 \( t=\sqrt[n]{\frac{ax+b}{cx+d}} \) とおいて置換積分する。
(3) \( f(\sqrt{a^2-x^2}) \ (a>0) \) という形の場合は、 \( x=a\sin \theta \) とおいて置換積分する。
(4) \( f(\sqrt{a^2+x^2}) \ (a>0) \) という形の場合は、 \( x=a\tan \theta \) もしくは \( x=a\sinh t \) とおいて置換積分する。
(5) \( f(\sqrt{x^2-a^2}) \ (a>0) \) という形の場合は、 \( x=\frac{a}{\cos \theta} \) とおいて置換積分する。
(6) \( f(x, \ \sqrt{ax^2+bx+c}) \ (a\not=0) \) という形の場合は、 \( a \) の正負によって次のように解く。
\( a>0 \) のとき: \( \sqrt{ax^2+bx+c}=t-\sqrt{a}x \) とおいて置換積分する。
\( a<0 \) のとき: \( ax^2+bx+c=0 \) の2つの実数解を \( \alpha,\beta \ (\alpha<\beta) \) とする。このとき、 \( t=\sqrt{\frac{x-\alpha}{\beta-x}} \) とおいて置換積分する。
定理10の証明(気になる方だけクリックしてください)
(1)を示します。
(1) \( t=\sqrt[n]{ax+b} \) とおくと、 \( t^n=ax+b \) となります。よって、
$$ x=\frac{t^n-b}{a}, \quad dx=\frac{nt^{n-1}}{a}dt $$
したがって、
$$ \int f(x, \ \sqrt[n]{ax+b})dx=\int f\left( \frac{t^n-b}{a}, \ t\right)\cdot \frac{nt^{n-1}}{a}dt $$
となり、有理関数の積分へと帰着することができます。
(1) \( \displaystyle \int \sqrt{\frac{1-x}{x}}dx \) を求める。
\( t=\sqrt{\frac{1-x}{x}} \) とおくと、 \( t^2=\frac{1-x}{x} \)
よって、
$$ x=\frac{1}{1+t^2}, \quad dx=\frac{-2t}{(1+t^2)^2}dt $$
したがって、
$$ \int \sqrt{\frac{1-x}{x}}dx=\int t\cdot\frac{-2t}{(1+t^2)^2}dt \tag{1} $$
さらに、 \( u=1+t^2 \) とおくと、 \( du=2tdt \) より、
$$ \frac{2t}{(1+t^2)^2}dt=\frac{1}{u^2}du $$
したがって、
$$ \int \frac{-2t}{(1+t^2)^2}dt=\int\frac{-1}{u^2}du=\frac{1}{u}=\frac{1}{1+t^2} $$
であるので、式(1)を部分積分すると、
$$ \begin{align} \int t\cdot\frac{-2t}{(1+t^2)^2}dt&=t\cdot \frac{1}{1+t^2}-\int \frac{1}{1+t^2}dt=\frac{t}{1+t^2}-\tan^{-1}t \\ &=\sqrt{x(1-x)}-\tan^{-1}\sqrt{\frac{1-x}{x}} \end{align} $$
(2) \( \displaystyle \int \frac{1}{\sqrt{(2-x)(x-1)}}dx \) を求める。
\( (2-x)(x-1)=-x^2+3x-2 \) より、 \( -x^2+3x-2=0 \) の実数解を求めると、 \( \alpha=1, \beta=2 \)
よって、 \( t=\sqrt{\frac{x-1}{2-x}} \) とおくと、 \( t^2=\frac{x-1}{2-x} \)
したがって、
$$ x=\frac{2t^2+1}{t^2+1}=2-\frac{1}{t^2+1}, \quad dx=\frac{2t}{(t^2+1)^2}dt $$
また、
$$ \sqrt{(2-x)(x-1)}=(2-x)\sqrt{\frac{x-1}{2-x}}=\frac{1}{t^2+1}\cdot t=\frac{t}{t^2+1} $$
よって、
$$ \begin{align} \int \frac{1}{\sqrt{(2-x)(x-1)}}dx&=\int \frac{t^2+1}{t}\cdot\frac{2t}{(t^2+1)^2}dt=\int \frac{2}{t^2+1}dt \\ &=2\tan^{-1}t=2\tan^{-1}\sqrt{\frac{x-1}{2-x}} \end{align} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

