こんにちは、ひかりです。
今回は微分積分学から平均値の定理・テイラー展開・ロピタルの定理について解説していきます。
この記事では以下のことを紹介します。
- ロルの定理と平均値の定理について
- テイラー展開・マクローリン展開について
- 不定形の極限値について
ロルの定理と平均値の定理
ロルの定理
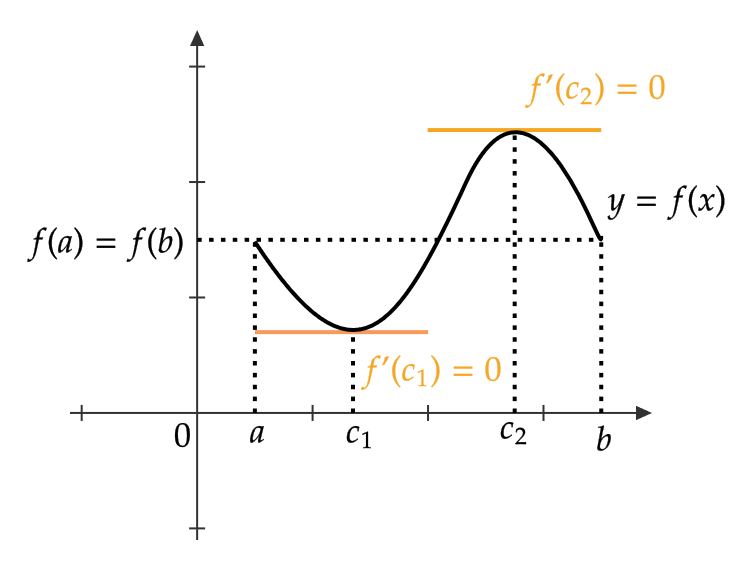
平均値の定理を考える前に、まず特別な場合であるロルの定理というものを考えます。
関数 \( y=f(x) \) がある閉区間 \( [a,b] \) 上で連続であり、開区間 \( (a,b) \) 上で微分可能とします。
そしてその関数が図のように \( f(a)=f(b) \) であるとき、開区間 \( (a,b) \) 上の接線の傾きを考えるとどこかしらで0となる点 \( c \) が存在します。(図のように1つとは限りません)
つまり、 \( x \) 軸に平行となる接線が必ず引けるということになります。
これをロルの定理と呼びます。まとめると、
閉区間 \( [a,b] \) 上で定義された連続関数 \( f \) が、開区間 \( (a,b) \) 上で微分可能で \( f(a)=f(b) \) であるとする。
このとき、 \( a \) と \( b \) の間に \( f'(c)=0 \) となる点 \( c \) が存在する。
定理1の証明(気になる方だけクリックしてください)
関数 \( y=f(x) \) が定理の仮定をみたすとすると、次の3つのうちのどれかが起きます。
- \( y=f(x) \) は定数関数
- \( y=f(x) \) は \( f(a)=f(b) \) よりも大きい値をとる \( x \) が存在する
- \( y=f(x) \) は \( f(a)=f(b) \) よりも小さい値をとる \( x \) が存在する
(2.と3.は同時におきる場合もあります。)
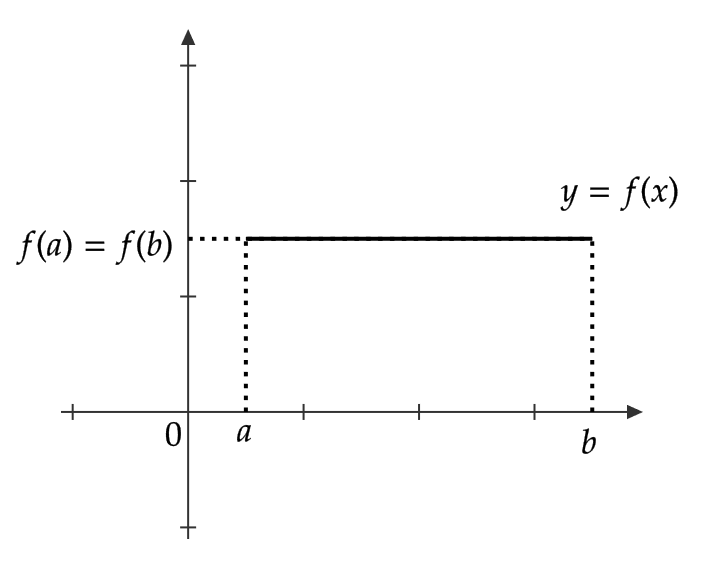
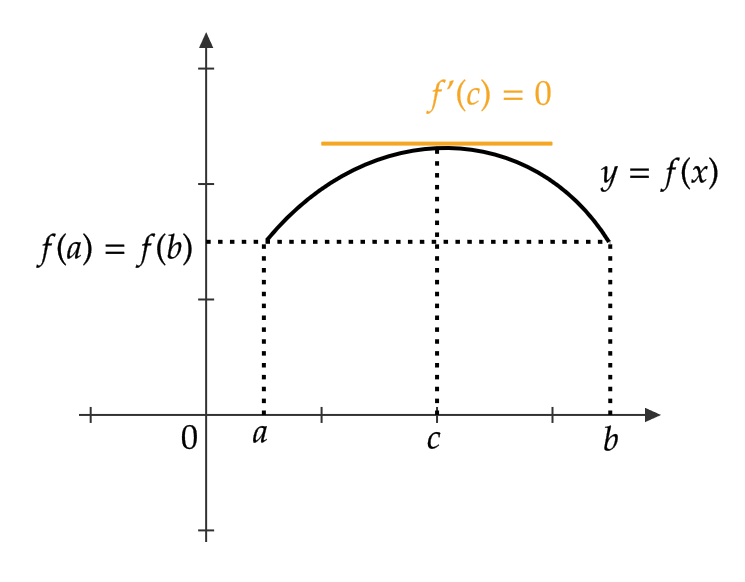
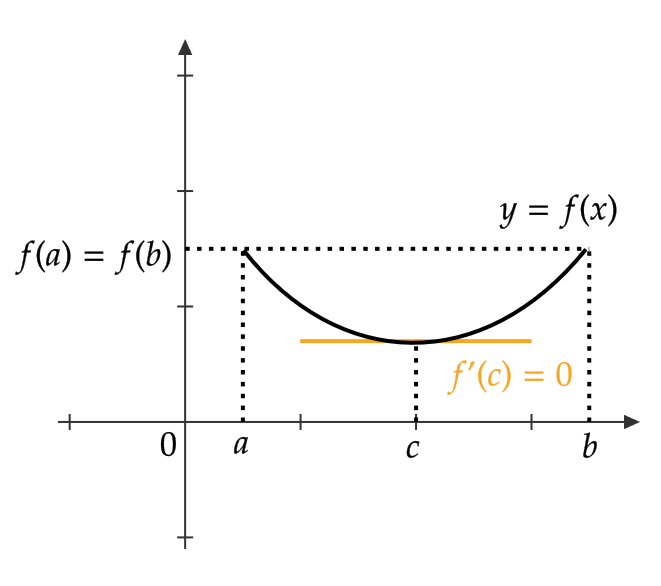
まず、1.の場合は前回の記事の定理8の(1)より、定数は微分すると0であるため、区間 \( [a,b] \) 上すべての点 \( c \) で \( f'(c)=0 \) となります。
よって、この場合は定理が成り立ちます。
次に、2.の場合を考えます。
前回の記事の定理5より、関数 \( y=f(x) \) は区間 \( (a,b) \) 上に最大値をもちます。
(\( y=f(x) \) は \( f(a)=f(b) \) よりも大きい値をとる点があるため、端点 \( a,b \) では最大値はとりません)
その最大値をもつ点を \( c \) とおきます。つまり、 \( f(c) \) が最大値です。
このとき、 \( a≦ x≦ b \) で \( f(x)-f(c)≦ 0 \) であるので、 \( \frac{f(x)-f(c)}{x-c} \) は
$$ \begin{cases} \frac{f(x)-f(c)}{x-c}≧0 & a<x<c \\ \frac{f(x)-f(c)}{x-c}≦0 & c<x<b \end{cases} $$
となります。
よって、 \( x\to c-0, \ x\to c+0 \) とすることにより、 \( f'(c)≧0 \) かつ \( f'(c)≦0 \) となります。
したがって、 \( f'(c)=0 \) となり、定理が成り立ちます。
最後に3.の場合ですが、このときは最小値をもつ点を \( c \) とおき、 \( \frac{f(x)-f(c)}{x-c} \) を考えれば同様の議論が成り立ちます。
平均値の定理
関数 \( y=f(x) \) がある閉区間 \( [a,b] \) 上で連続であり、開区間 \( (a,b) \) 上で微分可能とします。
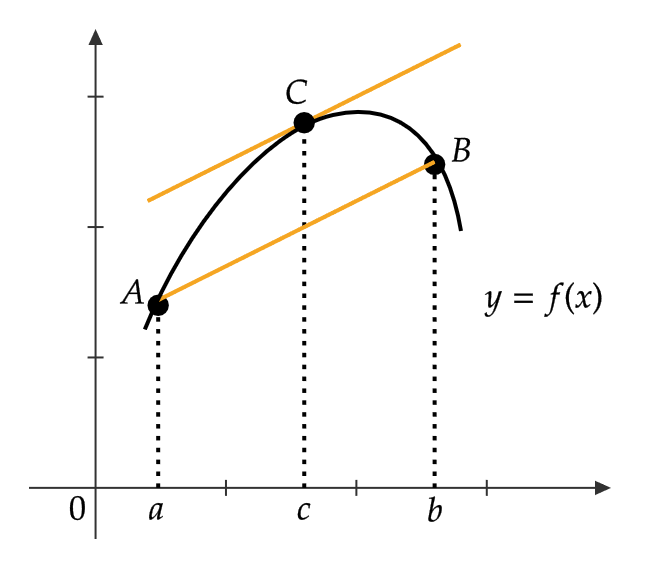
ここで、関数 \( y=f(x) \) のグラフ上の2点 \( A=(a,f(a)), \ B=(b,f(b)) \) を通る直線 \( AB \) を考えます。
このとき図のように、弧 \( AB \) 上にある適当な点 \( C=(c,f(c)) \) における接線は直線 \( AB \) と平行になります。
直線 \( AB \) の傾きは
$$ \frac{f(b)-f(a)}{b-a} $$
であり、点 \( C \) における接線の傾きは \( f'(c) \) であるので、
$$ \frac{f(b)-f(a)}{b-a}=f'(c) $$
となる点 \( c \) が \( a \) と \( b \) の間に存在します。
これを平均値の定理といいます。まとめると、
関数 \( y=f(x) \) がある閉区間 \( [a,b] \) 上で連続であり、開区間 \( (a,b) \) 上で微分可能ならば、
$$ \frac{f(b)-f(a)}{b-a}=f'(c) \quad (a<c<b) $$
をみたす点 \( c \) が存在する。
この定理はロルの定理を用いることで証明することができます。
定理2の証明(気になる方だけクリックしてください)
関数 \( g(x) \) を次のように定めます。
$$ g(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a) $$
\( f(x) \) が閉区間 \( [a,b] \) 上で連続であり、開区間 \( (a,b) \) 上で微分可能であるので、 \( g(x) \) も閉区間 \( [a,b] \) 上で連続であり、開区間 \( (a,b) \) 上で微分可能となります。
また、 \( g(a)=g(b)=0 \) となります。
よって、 \( g(x) \) はロルの定理の仮定をみたします。
$$ g'(x)=f'(x)-\frac{f(b)-f(a)}{b-a} $$
であるので、ロルの定理より \( a \) と \( b \) の間に
$$ g'(c)=f'(c)-\frac{f(b)-f(a)}{b-a}=0 $$
となる点 \( c \) が存在します。よって、
$$ f'(c)=\frac{f(b)-f(a)}{b-a} \quad (a<c<b) $$
となる点 \( c \) の存在がいえました。
(1) \( f(x)=x^2, \ a=1, \ b=3 \) のとき、平均値の定理をみたす点 \( c \) を求める。
$$ \frac{f(b)-f(a)}{b-a}=\frac{3^2-1^2}{3-1}=4, \quad f'(x)=2x $$
であるので、 \( 2x=4 \) となる \( x \) が \( c \) となる。
よって、 \( c=2 \)
(2) \( a>0 \) のとき、次の不等式が成り立つことを示す。
$$ a<e^a-1<ae^a $$
\( f(x)=e^x \) とおくと、 \( f(x) \) は実数全体で微分可能で \( f'(x)=e^x \) であるので、区間 \( [0,a] \) で平均値の定理を用いると、
$$ \frac{e^a-e^0}{a-0}=e^c \quad (0<c<a) $$
ここで、 \( \frac{e^a-e^0}{a-0}=\frac{e^a-1}{a} \)
また、 \( e^x \) は増加関数で \( 0<c<a \) より、
$$ 1<e^c<e^a $$
したがって、
$$ 1<\frac{e^a-1}{a}<e^a $$
\( a>0 \) より、
$$ a<e^a-1<ae^a $$
テイラー展開・マクローリン展開
テイラーの定理とマクローリンの定理
関数 \( y=f(x) \) が2階以上の導関数をもつとき、平均値の定理は次のように拡張することができます。
関数 \( y=f(x) \) が閉区間 \( [a,b] \) で \( n \) 回微分可能であるとする。このとき、次が成り立つ。
$$ \begin{align} f(b)&=f(a)+\frac{f'(a)}{1!}(b-a)+\frac{f^{\prime\prime}(a)}{2!}(b-a)^2+\frac{f^{\prime\prime\prime}(a)}{3!}(b-a)^3 \\ &\quad +\cdots+\frac{f^{(n-1)}(a)}{(n-1)!}(b-a)^{n-1}+R_n \\ &=\sum_{r=0}^{n-1}\frac{(b-a)^r}{r!}f^{(r)}(a)+R_n \end{align} $$
ここで、
$$ R_n=\frac{f^{(n)}(c)}{n!}(b-a)^n \quad (a<c<b) $$
をみたす \( c \) が存在する。この \( R_n \) をラグランジュの剰余項という。
定理3の証明(気になる方だけクリックしてください)
まず、
$$ f(b)-\sum_{r=0}^{n-1}\frac{(b-a)^r}{r!}f^{(r)}(a)-\frac{(b-a)^n}{n!}\theta=0 \tag{1} $$
となるように \( \theta \) を定めます。このとき、 \( \theta \) を求めます。
そのために、関数 \( g(x) \) を次のように定めます。
$$ g(x)=f(b)-\sum_{r=0}^{n-1}\frac{(b-x)^r}{r!}f^{(r)}(x)-\frac{(b-x)^n}{n!}\theta $$
このとき、
$$ \begin{align} g(b)&=f(b)-\sum_{r=0}^{n-1}\frac{(b-b)^r}{r!}f^{(r)}(b)-\frac{(b-b)^n}{n!}\theta \\ &=f(b)-f(b)-0 \quad (r=0 のとき (b-b)^0=1 に注意) \\ &=0 \end{align} $$
また、 \( \theta \) の定め方より、 \( g(a)=0 \) となります。
さらに、
$$ \begin{align} g'(x)&=0-\left\{ \frac{(b-x)^0}{0!}f^{(0)}(x)\right\}’-\sum_{r=1}^{n-1}\left\{ \frac{(b-x)^r}{r!}f^{(r)}(x) \right\}’-\frac{\theta}{n!}((b-x)^{n})’ \\ &=-f'(x)-\sum_{r=1}^{n-1}\left\{ -\frac{r(b-x)^{r-1}}{r!}f^{(r)}(x)+\frac{(b-x)^r}{r!}f^{(r+1)}(x)\right\}-\frac{\theta}{n!}\cdot (-n(b-x)^{n-1}) \\ &=-\frac{(b-x)^{n-1}}{(n-1)!}f^{(n)}(x)+\frac{(b-x)^{n-1}}{(n-1)!}\theta \quad (r=0,1,\cdots ,n-2 までの項はちょうど消えます) \\ &=-\frac{(b-x)^{n-1}}{(n-1)!}\{ f^{(n)}(x)-\theta\} \end{align} $$
となります。よって、ロルの定理を用いると、
$$ g'(c)=-\frac{(b-c)^{n-1}}{(n-1)!}\{ f^{(n)}(c)-\theta \}=0 \quad (a<c<b) $$
となる点 \( c \) が存在します。ここで、 \( -\frac{(b-c)^{n-1}}{(n-1)!}\not=0 \) であるので、
$$ f^{(n)}(c)-\theta=0 $$
よって、
$$ \theta=f^{(n)}(c) $$
となり、 \( \theta \) が求まりました。よって、はじめの式(1)に \( \theta=f^{(n)}(c) \) を代入すると、
$$ f(b)-\sum_{r=0}^{n-1}\frac{(b-a)^r}{r!}f^{(r)}(a)-\frac{(b-a)^n}{n!}f^{(n)}(c)=0 $$
ここで、 \( R_n=\frac{(b-a)^n}{n!}f^{(n)}(c) \) とおけば、
$$ f(b)=\sum_{r=0}^{n-1}\frac{(b-a)^r}{r!}f^{(r)}(a)+R_n $$
となり、定理が成り立ちます。
また、テイラーの定理において、 \( a=0, \ b=x \) とおくことにより、次の定理が成り立ちます。
関数 \( y=f(x) \) が \( x=0 \) を含む区間で \( C^n \) 級であれば、次が成り立つ。
$$ \begin{align} f(x)&=f(0)+\frac{f'(0)}{1!}x+\frac{f^{\prime\prime}(0)}{2!}x^2+\frac{f^{\prime\prime\prime}(0)}{3!}x^3 \\ &\quad +\cdots+\frac{f^{(n-1)}(0)}{(n-1)!}x^{n-1}+R_n \\ &=\sum_{r=0}^{n-1}\frac{f^{(r)}(0)}{r!}x^r+R_n \end{align} $$
ここで、
$$ R_n=\frac{f^{(n)}(c)}{n!}x^n \quad (c \ は \ 0 \ と \ x \ の間にある) $$
をみたす \( c \) が存在する。
この定理は関数 \( y=f(x) \) が \( x=0 \) の近くで \( n \) 回微分可能であるならば、 \( x=0 \) の近くでその関数は \( n \) 次多項式で近似することができる、ということをいっています。
特に、関数 \( f(x) \) は多項式に限らず一般の関数でよいということがこの定理の主張のすごいところになります。
\( f(x)=x^2e^x \) を \( x=0 \) の近くにおいて3次多項式で近似することを考える。
$$ f'(x)=2xe^x+x^2e^x $$
$$ f^{\prime\prime}(x)=2e^x+4xe^x+x^2e^x $$
$$ f^{\prime\prime\prime}(x)=6e^x+6xe^x+x^2e^x $$
であるので、マクローリンの定理を3次の項までで用いると、
$$ \begin{align} f(x)&=f(0)+\frac{f'(0)}{1!}x+\frac{f^{\prime\prime}(0)}{2!}x^2+\frac{f^{\prime\prime\prime}(0)}{3!}x^3+R_n \\ &=x^2+x^3+R_n \end{align} $$
ここで、 \( x=0 \) の近くで \( R_n=\frac{f^{(4)}(c)}{4!}x^4 \) は \( x^2, \ x^3 \) の項に比べて十分小さくすることができるので、
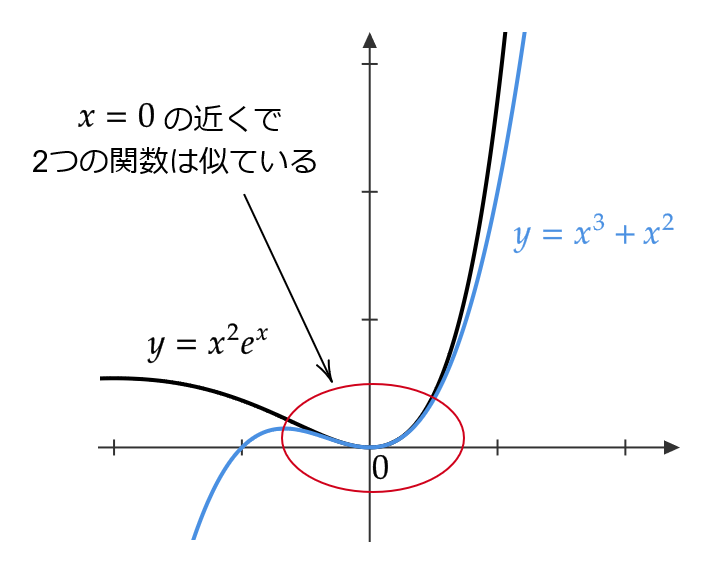
$$ f(x)≒x^3+x^2 \quad (x=0 の近くにおいて) $$
つまり、 \( f(x) \) は \( x=0 \) の近くで \( x^3+x^2 \) で近似することができる。
実際、グラフを見てみると、 \( x=0 \) の近くで似ていることがわかります。
テイラーの定理で \( a \) はそのままで \( b=x \) とおくことにより、 \( x=a \) の近くでの多項式近似も得ることができます。
関数 \( y=f(x) \) が \( x=a \) を含む区間で \( C^n \) 級であれば、次が成り立つ。
$$ \begin{align} f(x)&=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^3 \\ &\quad +\cdots+\frac{f^{(n-1)}(a)}{(n-1)!}(x-a)^{n-1}+R_n \\ &=\sum_{r=0}^{n-1}\frac{f^{(r)}(a)}{r!}(x-a)^r+R_n \end{align} $$
ここで、
$$ R_n=\frac{f^{(n)}(c)}{n!}(x-a)^n \quad (c \ は \ a \ と \ x \ の間にある) $$
をみたす \( c \) が存在する。
テイラー級数・マクローリン級数
関数 \( y=f(x) \) が \( x=a \) を含む区間で \( C^{\infty} \) 級であるとします。
このとき、定理5における \( f(x) \) の式
$$ f(x)=\sum_{r=0}^{n-1}\frac{f^{(r)}(a)}{r!}(x-a)^r+R_n $$
の両辺を \( n\to\infty \) とすることを考えます。
左辺は \( f(x) \) は \( n \) に関係ないため \( \displaystyle \lim_{n\to\infty}f(x)=f(x) \) となります。
右辺は
$$ \lim_{n\to\infty}\sum_{r=0}^{n-1}\frac{f^{(r)}(a)}{r!}(x-a)^r+\lim_{n\to \infty}R_n $$
ここで、もし \( \displaystyle \lim_{n\to \infty}R_n=0 \) であったとします。すると、
$$ f(x)=\lim_{n\to\infty}\sum_{r=0}^{n-1}\frac{f^{(r)}(a)}{r!}(x-a)^r $$
つまり、無限級数 \( \displaystyle \sum_{r=0}^{\infty}\frac{f^{(r)}(a)}{r!}(x-a)^r \) は \( f(x) \) に収束します。
まとめると、次のことがいえます。
関数 \( y=f(x) \) が \( x=a \) を含む区間 \( I \) で \( C^{\infty} \) 級であり、 \( I \) のすべての点で
$$ \lim_{n\to\infty}R_n=0 $$
をみたすとき、 \( f \) は \( I \) 上で
$$ \begin{align} f(x)&=\sum_{r=0}^{\infty}\frac{f^{(r)}(a)}{r!}(x-a)^r \\ &=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f^{\prime\prime}(a)}{2!}(x-a)^2+\frac{f^{\prime\prime\prime}(a)}{3!}(x-a)^3 \\ &\quad +\cdots+\frac{f^{n}(a)}{n!}(x-a)^{n}+\cdots \end{align} $$
の形の級数で表される。この級数を \( f(x) \) の \( x=a \) でのテイラー級数といい、 \( f(x) \) をテイラー級数の形で表すことをテイラー展開といいます。
特に、 \( x=0 \) でのテイラー級数をマクローリン級数ともいい、\( f(x) \) をマクローリン級数の形で表すことをマクローリン展開といいます。つまり、
$$ \begin{align} f(x)&=\sum_{r=0}^{\infty}\frac{f^{(r)}(0)}{r!}x^r \\ &=f(0)+\frac{f'(0)}{1!}x+\frac{f^{\prime\prime}(0)}{2!}x^2+\frac{f^{\prime\prime\prime}(0)}{3!}x^3+\cdots+\frac{f^{n}(0)}{n!}x^{n}+\cdots \end{align} $$
ここで、有名な関数のマクローリン展開を表にまとめておきます。
表の後の例にて、いくつかの関数の導関数を実際に求めています。
| 関数のマクローリン展開 |
| $$ e^x=1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+\cdots \quad (|x|<\infty) $$ |
| $$ \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+(-1)^n\frac{x^{2n+1}}{(2n+1)!}+\cdots \quad (|x|<\infty) $$ |
| $$ \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\cdots+(-1)^n\frac{x^{2n}}{(2n)!}+\cdots \quad (|x|<\infty) $$ |
| $$ \log (1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\cdots +(-1)^{n-1}\frac{x^n}{n}+\cdots \quad (-1<x≦1) $$ |
| $$ (1+x)^{\alpha}=1+\alpha x+\frac{\alpha(\alpha-1)}{2!}x^2+\cdots+\frac{\alpha(\alpha-1)\cdots(\alpha-n+1)}{n!}x^n+\cdots \quad (|x|<1) $$ |
| $$ \frac{1}{1+x}=1-x+x^2-\cdots+(-1)^nx^n+\cdots \quad (|x|<1) $$ |
| $$ \frac{1}{1-x}=1+x+x^2+\cdots+x^n+\cdots \quad (|x|<1) $$ |
マクローリン展開を求めるための準備として、 \( \displaystyle \lim_{n\to\infty}\frac{|x|^n}{n!} \) を求める。
各点 \( x \) に対して、 \( m \) を \( m≧2|x| \) となる自然数とする。すると、 \( n≧m \) のとき、
$$ \begin{align} \frac{|x|^n}{n!}&=\frac{|x|^m}{m!}\cdot \frac{|x|}{m+1}\cdot \frac{|x|}{m+2} \cdot \cdots \cdot \frac{|x|}{n} \\ &≦\frac{|x|^m}{m!}\cdot \frac{\frac{m}{2}}{m+1}\cdot \frac{\frac{m}{2}}{m+2} \cdot \cdots \cdot \frac{\frac{m}{2}}{n} \\ &=\left( \frac{1}{2} \right)^{n-m}\frac{|x|^m}{m!}\cdot \frac{m}{m+1}\cdot \frac{m}{m+2} \cdot \cdots \cdot \frac{m}{n} \\ &≦ \frac{2^m|x|^m}{m!}\left(\frac{1}{2}\right)^n \quad (\frac{m}{m+1}\cdot \frac{m}{m+2} \cdot \cdots \cdot \frac{m}{n}≦1に注意) \end{align} $$
よって、
$$ \lim_{n\to\infty}\frac{|x|^n}{n!}≦\frac{2^m|x|^m}{m!}\lim_{n\to\infty}\left(\frac{1}{2}\right)^n=0 $$
一方で、 \( \frac{|x|^n}{n!}≧0 \) であるので、はさみうちの原理より、
$$ \lim_{n\to\infty}\frac{|x|^n}{n!}=0 $$
(1) \( f(x)=e^x \) をマクローリン展開する。
任意の自然数に対して、 \( f^{(n)}(x)=e^x \) であるので、
$$ R_n=\frac{f^{(n)}(c)}{n!}x^n=\frac{e^c}{n!}x^n \quad (0<|c|<|x|) $$
ここで、 \( |c|<|x| \) であるので、先ほどの準備より、
$$ |R_n|=e^c\frac{|x|^n}{n!}<e^{|x|}\frac{|x|^n}{n!}\to 0 \ (n\to\infty) $$
(\( e^c<e^{|x|} \) としたのは \( c \) は \( n \) によって変わるので、 \( n\to\infty \) をするときに邪魔になるため)
よって、 \( \displaystyle \lim_{n\to \infty}R_n=0 \) がいえたので、あとはマクローリン級数の式に導関数を代入していけば、
$$ e^x=1+x+\frac{x^2}{2!}+\cdots+\frac{x^n}{n!}+\cdots \quad (|x|<\infty) $$
(2) \( f(x)=\sin x \) をマクローリン展開する。
\( \sin x \) を何回も微分していくと、
$$ (\sin x)’=\cos x=\sin \left(x+\frac{\pi}{2}\right) $$
$$ \begin{align} (\sin x)^{\prime\prime}&=\left\{ \sin \left(x+\frac{\pi}{2}\right) \right\}’=\cos \left(x+\frac{\pi}{2}\right) \\ &=\sin \left( \left(x+\frac{\pi}{2}\right)+\frac{\pi}{2} \right)=\sin (x+\pi) \end{align} $$
となるので、第 \( n \) 階導関数は
$$ (\sin x )^{(n)}=\sin \left(x+\frac{n\pi}{2} \right) $$
となる。(本当は数学的帰納法で証明) よって、
$$ R_n=\frac{f^{(n)}(c)}{n!}x^n=\frac{\sin \left(c+\frac{n\pi}{2} \right)}{n!}x^n \quad (0<|c|<|x|) $$
\( \left|\sin \left(c+\frac{n\pi}{2} \right)\right|≦1 \) であるので、先ほどの準備より、
$$ |R_n|=\left|\sin \left(c+\frac{n\pi}{2} \right)\right|\frac{|x|^n}{n!}≦\frac{|x|^n}{n!}\to 0 \ (n\to\infty) $$
よって、 \( \displaystyle \lim_{n\to \infty}R_n=0 \) がいえたので、あとはマクローリン級数の式に導関数を代入していけば、
$$ \sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\cdots+(-1)^n\frac{x^{2n+1}}{(2n+1)!}+\cdots \quad (|x|<\infty) $$
不定形の極限値
\( \displaystyle \lim_{x\to1}\frac{x^2-1}{x-1} \) のように、 \( \displaystyle \lim_{x\to a}\frac{f(x)}{g(x)} \) において \( \displaystyle \lim_{x\to a}f(x)=0 \) かつ \( \displaystyle \lim_{x\to a}g(x)=0 \) となる場合があります。
このとき、 \( \displaystyle \lim_{x\to a}\frac{f(x)}{g(x)} \) は分母分子がともに0に収束するので、極限値が一見求まらないように見えます。
( いまあげた例の場合は、 \( \displaystyle \lim_{x\to1}\frac{x^2-1}{x-1}=\lim_{x\to 1}(x+1)=2 \) と実は求められます)
このような場合を不定形といいます。この不定形の極限値を求める際に便利なロピタルの定理というものを紹介します。
コーシーの平均値の定理
まず、ロピタルの定理を証明するのに必要となるコーシーの平均値の定理を紹介します。
2つの関数 \( f(x), \ g(x) \) はともにある閉区間 \( [a,b] \) 上で連続であり、開区間 \( (a,b) \) 上で微分可能であるとする。
また、 \( g'(x) \) は \( (a,b) \) 上で0ではないとする。
このとき、
$$ \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(c)}{g'(c)} \quad (a<c<b) $$
となる点 \( c \) が存在する。
定理7の証明(気になる方だけクリックしてください)
まず、 \( g(x) \) に対して平均値の定理を用いると、
$$ g(b)-g(a)=(b-a)g'(\alpha) \quad (a<\alpha<b) $$
となる点 \( \alpha \) が存在します。ここで定理の仮定より、 \( g'(\alpha)\not=0 \) であるので、
$$ g(b)-g(a)\not=0 $$
よって、 \( \beta \) を次のように定めます。
$$ \frac{f(b)-f(a)}{g(b)-g(a)}=\beta $$
これは次のようになります。
$$ f(b)-f(a)-\beta(g(b)-g(a))=0 $$
これを用いて関数 \( h(x) \) を次のように定めます。
$$ h(x)=f(b)-f(x)-\beta(g(b)-g(x)) $$
すると、 \( h(a)=h(b)=0 \) であり、
$$ h'(x)=-f'(x)+\beta g'(x) $$
よって、ロルの定理より、
$$ h'(c)=-f'(c)+\beta g'(c)=0 \quad (a<c<b) $$
となる点 \( c \) が存在します。これより、 \( \beta=\frac{f'(c)}{g'(c)} \)
したがって、
$$ \frac{f(b)-f(a)}{g(b)-g(a)}=\beta=\frac{f'(c)}{g'(c)} \quad (a<c<b) $$
となり、定理が成り立ちます。
ロピタルの定理
いよいよ、ロピタルの定理を紹介します。
2つの関数 \( f(x), \ g(x) \) は \( x=a \) の近くで連続で、 \( x=a \) 以外では微分可能であるとする。
さらに、 \( f(a)=g(a)=0 \) で \( x=a \) 以外では \( g'(x)\not=0 \) とする。
このとき、
$$ \lim_{x\to a}\frac{f'(x)}{g'(x)}=\ell $$
であれば、
$$ \lim_{x\to a}\frac{f(x)}{g(x)}=\ell $$
定理8の証明(気になる方だけクリックしてください)
コーシーの平均値の定理より、 \( a \) の近くに \( x \) をとると、
$$ \frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f'(c)}{g'(c)} \quad (c \ は \ a \ と \ x \ の間にある) $$
となる点 \( c \) が存在します。
ここで定理の仮定より、 \( f(a)=g(a)=0 \) であるため、
$$ \frac{f(x)}{g(x)}=\frac{f'(c)}{g'(c)} $$
よって、 \( x\to a \) のとき \( c\to a \) であるので、
$$ \lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{c\to a}\frac{f'(c)}{g'(c)}=\lim_{x\to a}\frac{f'(x)}{g'(x)}=\ell $$
したがって、定理が成り立ちます。
(1) \( \displaystyle \lim_{x\to1}\frac{x^2-1}{x-1} \) をロピタルの定理を用いて計算する。
ロピタルの定理の条件をみたすことは先ほど説明しました。
よって、ロピタルの定理を用いると、
$$ \lim_{x\to1}\frac{x^2-1}{x-1}=\lim_{x\to 1}\frac{2x}{1}=2 $$
(2) \( \displaystyle \lim_{x\to0}\frac{e^x-\cos x}{\sin x} \) をロピタルの定理を用いて計算する。
まず、
$$ \lim_{x\to0}(e^x-\cos x)=0, \ \lim_{x\to 0}\sin x=0 $$
より、この極限は \( \frac{0}{0} \) の不定形となる。
よって、ロピタルの定理を用いると、
$$ \lim_{x\to 0}\frac{e^x-\cos x}{\sin x}=\lim_{x\to 0}\frac{e^x+\sin x}{\cos x}=\frac{1+0}{1}=1 $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

