こんにちは、ひかりです。
今回は微分積分学から三角関数と逆三角関数について解説していきます。
この記事では以下のことを紹介します。
- 三角関数の性質のまとめ
- 余割関数・正割関数・余接関数について
- 逆三角関数とそのグラフについて
- 逆余割関数・逆正割関数・逆余接関数について
三角関数の性質のまとめ
ここでは、高校数学で学んだ三角関数の性質を振り返っていきます。
三角関数の定義やグラフについて詳しく知りたい方は以下の記事をご覧ください。
まず、三角関数において一番重要といっても過言ではない定理である加法定理という公式がありました。
(1) \( \sin\theta \) の加法定理
$$ \begin{align} \sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \sin(\alpha-\beta)&=\sin\alpha\cos\beta-\cos\alpha\sin\beta \end{align} $$
(2) \( \cos\theta \) の加法定理
$$ \begin{align} \cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta \\ \cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{align} $$
(3) \( \tan\theta \) の加法定理
$$ \begin{align} \tan(\alpha+\beta)&=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \\ \tan(\alpha-\beta)&=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{align} $$
この加法定理を用いると、三角関数のさまざまな性質を示すことができます。
ここでは、高校数学で学んだ三角関数の性質をまとめて見ていきましょう。
(1) (三角関数の負角公式)
$$ \sin(-x)=-\sin x \quad \cos(-x)=\cos x \quad \tan(-x)=-\tan x $$
(2) (三角関数の余角公式)
$$ \sin\left(\frac{\pi}{2}+x\right)=\cos x \quad \sin\left(\frac{\pi}{2}-x\right)=\cos x $$
$$ \cos\left(\frac{\pi}{2}+x\right)=-\sin x \quad \cos\left(\frac{\pi}{2}-x\right)=\sin x $$
(3) (三角関数の補角公式)
$$\sin(\pi+x)=-\sin x \quad \sin(\pi-x)=\sin x $$
$$\cos(\pi+x)=-\cos x \quad \cos(\pi-x)=-\cos x $$
(1) (三角関数の2倍角の公式)
$$ \begin{align} \sin 2\theta&=2\sin\theta\cos\theta \\ \cos2\theta&=\cos^2\theta-\sin^2\theta=2\cos^2\theta-1=1-2\sin^2\theta \\ \tan2\theta&=\frac{2\tan\theta}{1-\tan^2\theta} \end{align} $$
(2) (三角関数の3倍角の公式)
$$ \begin{align} \sin 3\theta&=3\sin\theta-4\sin^3\theta \\ \cos3\theta&=-3\cos\theta+4\cos^3\theta \\ \tan3\theta&=\frac{3\tan\theta-\tan^3\theta}{1-3\tan^2\theta} \end{align} $$
(3) (三角関数の半角公式)
$$ \begin{align} \sin^2\frac{\theta}{2}&=\frac{1}{2}(1-\cos\theta) \\ \cos^2\frac{\theta}{2}&=\frac{1}{2}(1+\cos\theta) \\ \tan^2\frac{\theta}{2}&=\frac{\sin^2\frac{\theta}{2}}{\cos^2\frac{\theta}{2}}=\frac{1-\cos\theta}{1+\cos\theta} \end{align} $$
(1) $$ \sin\alpha\cos\beta=\frac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\} $$
(2) $$ \cos\alpha\sin\beta=\frac{1}{2}\{\sin(\alpha+\beta)-\sin(\alpha-\beta)\} $$
(3) $$ \cos\alpha\cos\beta=\frac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\} $$
(4) $$ \sin\alpha\sin\beta=-\frac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\} $$
(5) $$ \sin A+\sin B=2\sin\frac{A+B}{2}\cos\frac{A-B}{2} $$
(6) $$ \sin A-\sin B=2\cos\frac{A+B}{2}\sin\frac{A-B}{2} $$
(7) $$ \cos A+\cos B=2\cos\frac{A+B}{2}\cos\frac{A-B}{2} $$
(8) $$ \cos A-\cos B=-2\sin\frac{A+B}{2}\sin\frac{A-B}{2} $$
定理4については以下の記事でも詳しく紹介しています。
余割関数・正割関数・余接関数
ここまで紹介してきた三角関数 \( \sin \theta, \ \cos\theta, \ \tan\theta \) はそれぞれ正弦関数、余弦関数、正接関数と呼びます。
この \( \sin \theta, \ \cos\theta, \ \tan \theta \) の逆数をそれぞれ \( \csc \theta, \ \sec \theta, \ \cot \theta \) と表します。つまり、
$$ \csc \theta=\frac{1}{\sin \theta}, \ \sec \theta=\frac{1}{\cos\theta}, \ \cot \theta=\frac{1}{\tan \theta} $$
これらはそれぞれコセカント(cosecant)、セカント(secant)、コタンジェント(cotangent)もしくは余割関数、正割関数、余接関数と呼びます。
ただし、 \( \csc \theta, \ \sec \theta, \ \cot \theta \) はそれぞれ \( \sin \theta, \ \cos\theta, \ \tan \theta \) が0となるときには定義されないことに注意してください。
(1) \( \sec \left(\frac{\pi}{3} \right) \) を求める。
$$ \sec \left(\frac{\pi}{3} \right)=\frac{1}{\cos \left( \frac{\pi}{3} \right)}=\frac{1}{\frac{1}{2}}=2 $$
(2) \( \cot \left(\frac{\pi}{6} \right) \) を求める。
$$ \cot \left(\frac{\pi}{6} \right)=\frac{1}{\tan \left( \frac{\pi}{6} \right)}=\frac{1}{\frac{1}{\sqrt{3}}}=\sqrt{3} $$
(3) \( \csc \left(\frac{\pi}{3} \right) \) を求める。
$$ \csc \left(\frac{\pi}{3} \right)=\frac{1}{\sin \left( \frac{\pi}{3} \right)}=\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2}{\sqrt{3}} $$
\( \csc \theta, \ \sec \theta, \ \cot \theta \) に関して、次の性質が成り立ちます。
$$ \cot \theta=\frac{\cos\theta}{\sin \theta}, \quad 1+\tan^2\theta=\sec^2\theta, \quad 1+\cot^2\theta=\csc^2\theta $$
定理5の証明(気になる方だけクリックしてください)
$$ \cot \theta=\frac{1}{\tan\theta}=\frac{1}{\frac{\sin\theta}{\cos\theta}}=\frac{\cos\theta}{\sin\theta} $$
$$ 1+\tan^2\theta=\frac{1}{\cos^2\theta}=\sec^2\theta $$
$$ 1+\cot^2\theta=1+\frac{1}{\tan^2\theta}=\frac{\tan^2\theta+1}{\tan^2\theta}=\frac{\frac{1}{\cos^2\theta}}{\frac{\sin^2\theta}{\cos^2\theta}}=\frac{1}{\sin^2\theta}=\csc^2\theta $$
\( \csc \theta, \ \sec \theta, \ \cot \theta \) のグラフについては、後ほど考えます。
逆三角関数とそのグラフ
逆三角関数の定義
三角関数の逆関数について考えましょう。
逆関数については以下の記事で紹介していますのでご覧ください。
ここで、定理2の(3)を2回用いると、 \( \sin (x+2\pi)=\sin x \) であることが分かります。
よって、そのままでは三角関数の逆関数を考えることができません。
なぜなら、 \( y=\sin (x+2\pi)=\sin x \) とおいて \( y \) を変数だと思い逆関数を考えると、この \( y \) に対して \( x, \ x+2\pi \) の2つの値を返すからです。
(関数は1つの変数に対して、1つの値を返すものでした。)
そこで、関数の定義域を制限する必要が出てきます。
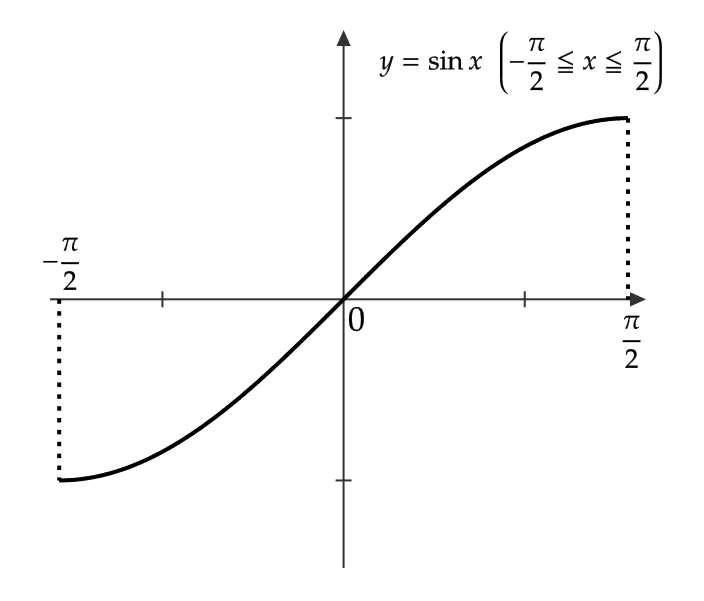
(1) \( \sin x \) の \( -\frac{\pi}{2}≦x≦ \frac{\pi}{2} \) での逆関数を \( \sin^{-1}x \) もしくは \( \arcsin x \) で表し、アークサインもしくは逆正弦関数という。
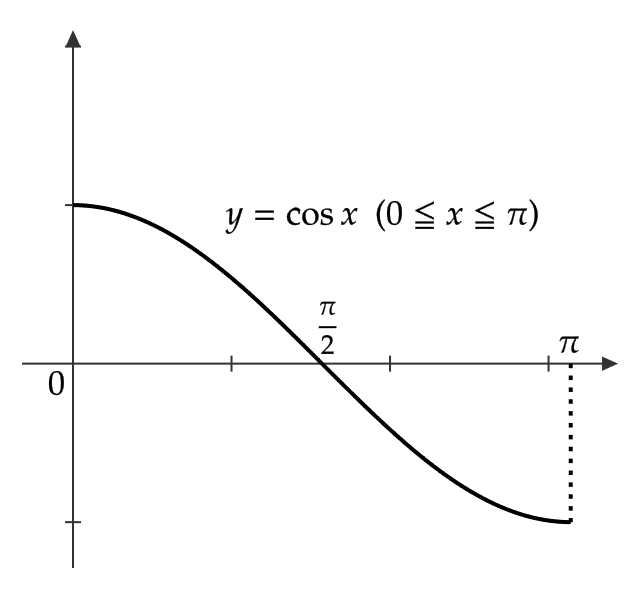
(2) \( \cos x \) の \( 0≦ x ≦ \pi \) での逆関数を \( \cos^{-1}x \) もしくは \( \arccos x \) で表し、アークコサインもしくは逆余弦関数という。
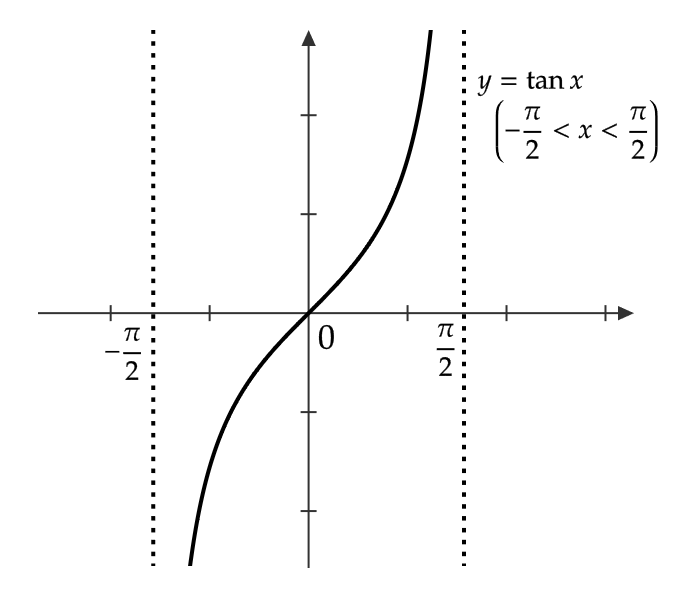
(3) \( \tan x \) の \( -\frac{\pi}{2}< x <\frac{\pi}{2} \) での逆関数を \( \tan^{-1}x \) もしくは \( \arctan x \) で表し、アークタンジェントもしくは逆正接関数という。
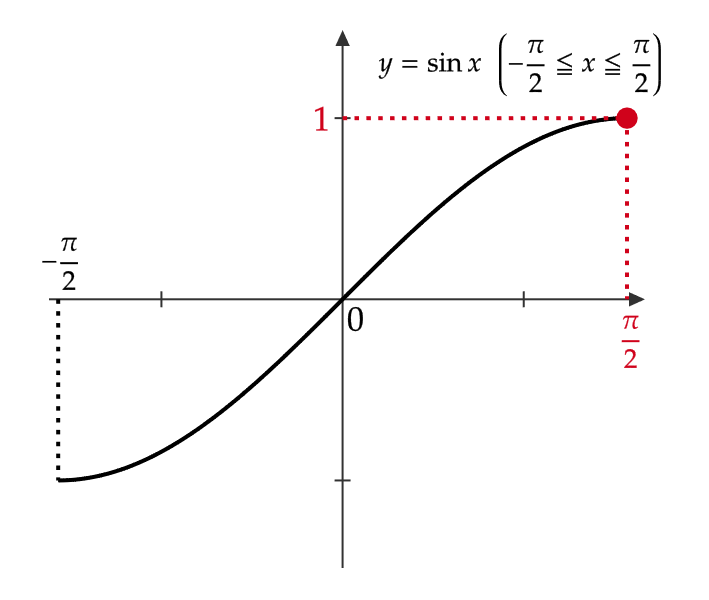
(1) \( \sin^{-1}1 \) を求める。
\( \sin^{-1}1=\theta \) とおくと、これは
$$ 1=\sin\theta \ \left( -\frac{\pi}{2}≦ \theta≦ \frac{\pi}{2} \right) $$
と同値。よって、 \( \sin^{-1}1=\theta=\frac{\pi}{2} \)
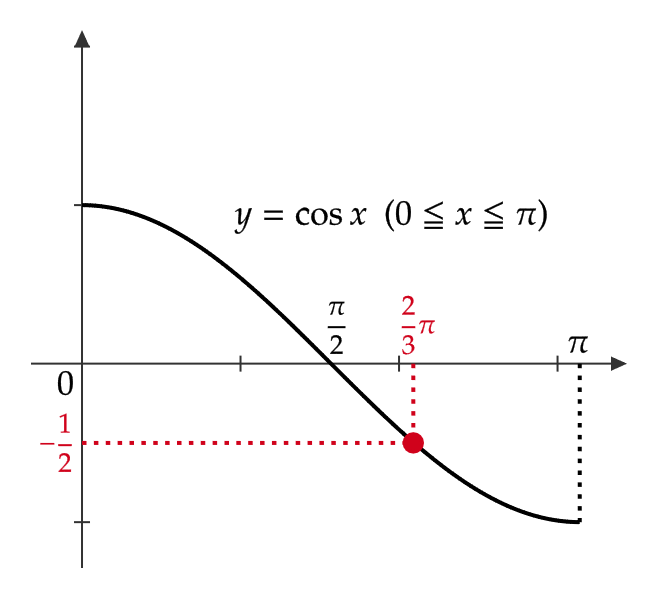
(2) \( \cos^{-1}\left( -\frac{1}{2}\right) \) を求める。
\( \cos^{-1}\left( -\frac{1}{2}\right)=\theta \) とおくと、これは
$$ -\frac{1}{2}=\cos\theta \ ( 0≦ \theta≦ \pi) $$
と同値。よって、 \( \cos^{-1}\left( -\frac{1}{2}\right)=\theta=\frac{2}{3}\pi \)
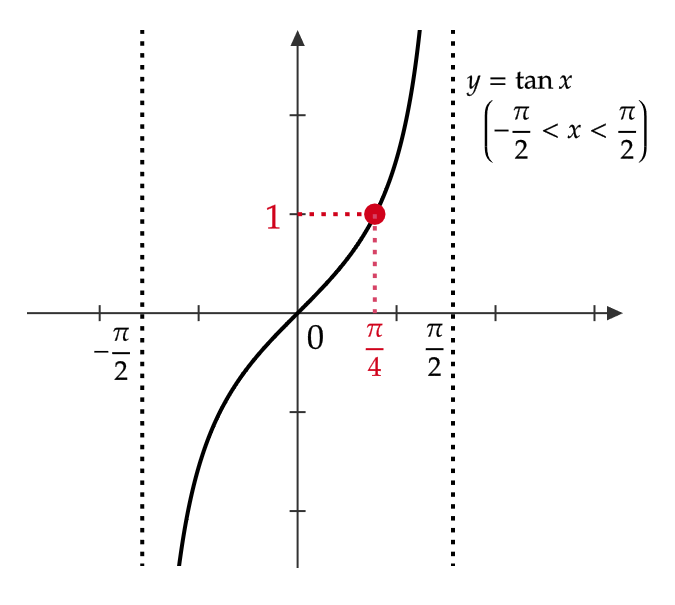
(3) \( \tan^{-1}1 \) を求める。
\( \tan^{-1}1=\theta \) とおくと、これは
$$ 1=\tan\theta \ \left( -\frac{\pi}{2}< \theta< \frac{\pi}{2} \right) $$
と同値。よって、 \( \tan^{-1}1=\theta=\frac{\pi}{4} \)
逆三角関数のグラフ
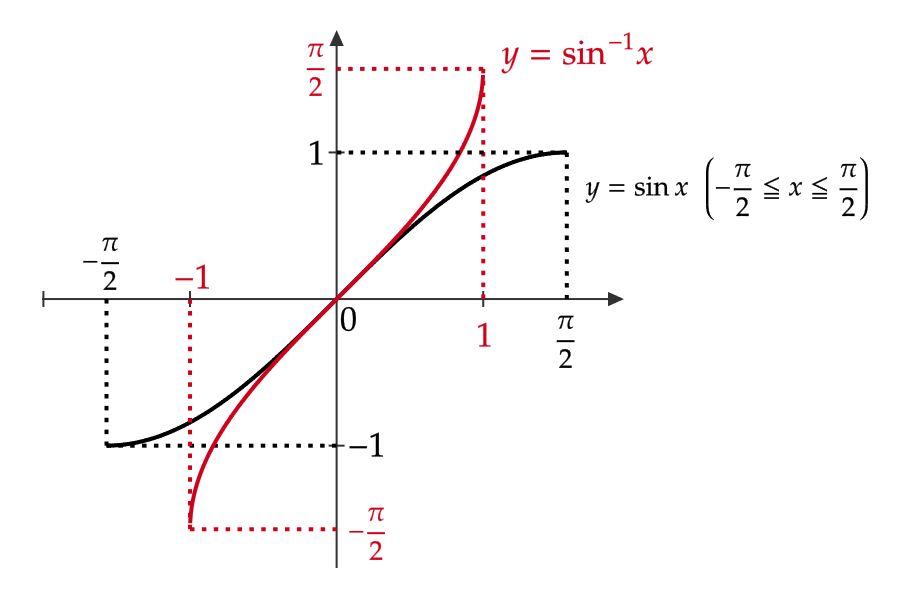
\( y=\sin^{-1}x \) のグラフ
\( y=\sin^{-1}x \) は \( y=\sin x \) の逆関数なので、 \( y=x \) に関して対称となります。
ただし、逆関数を考えるときは \( y=\sin x \) の定義域は \( -\frac{\pi}{2}≦ x≦ \frac{\pi}{2} \) 、値域は \( -1≦ y≦ 1 \) であるので、 \( y=\sin^{-1}x \) の定義域は \( -1≦ x≦ 1 \) 、値域は \( -\frac{\pi}{2}≦ y≦ \frac{\pi}{2} \) となります。
よって、次のようなグラフとなります。
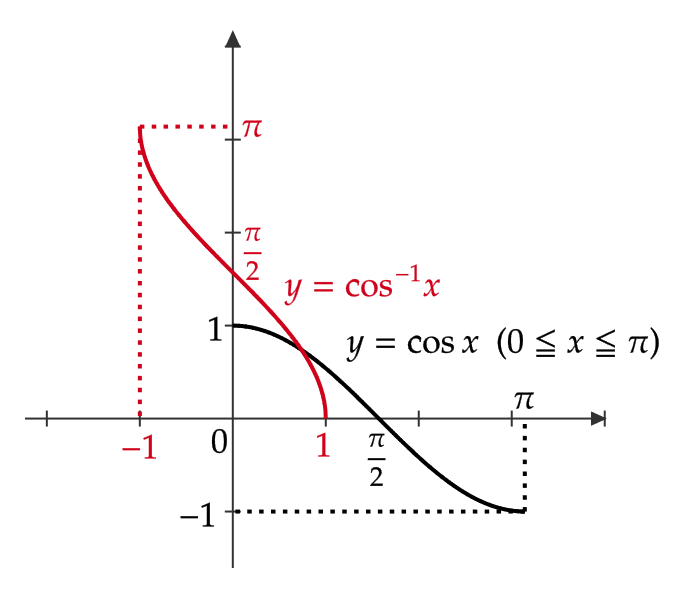
\( y=\cos^{-1}x \) のグラフ
\( y=\cos^{-1}x \) は \( y=\cos x \) の逆関数なので、 \( y=x \) に関して対称となります。
ただし、逆関数を考えるときは \( y=\cos x \) の定義域は \( 0≦ x≦ \pi \) 、値域は \( -1≦ y≦ 1 \) であるので、 \( y=\cos^{-1}x \) の定義域は \( -1≦ x≦ 1 \) 、値域は \( 0≦ y≦ \pi \) となります。
よって、次のようなグラフとなります。
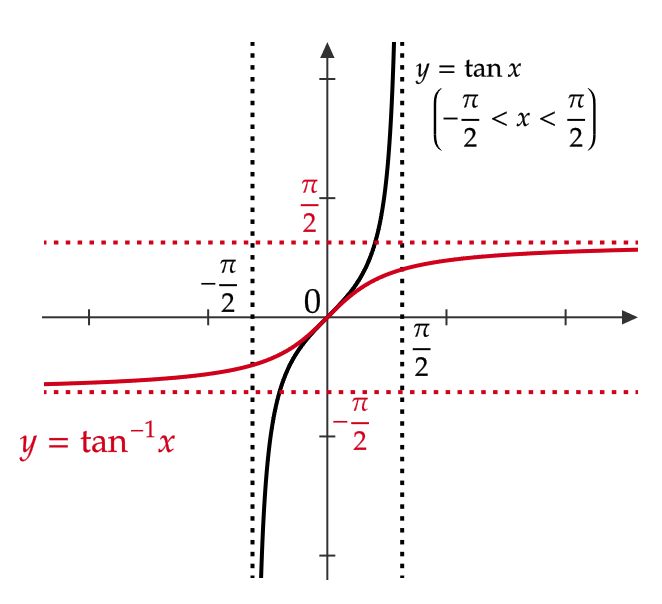
\( y=\tan^{-1}x \) のグラフ
\( y=\tan^{-1}x \) は \( y=\tan x \) の逆関数なので、 \( y=x \) に関して対称となります。
ただし、逆関数を考えるときは \( y=\tan x \) の定義域は \( -\frac{\pi}{2}< x< \frac{\pi}{2} \) 、値域は実数全体であるので、 \( y=\tan^{-1}x \) の定義域は実数全体 、値域は \( -\frac{\pi}{2}< y< \frac{\pi}{2} \) となります。
よって、次のようなグラフとなります。
最後に逆関数を考える際のそれぞれの関数の定義域と値域を表にまとめておきます。
| 関数 | 定義域 | 値域 |
| \( y=\sin x \) | \( -\frac{\pi}{2}≦ x≦ \frac{\pi}{2} \) | \( -1≦ y≦ 1 \) |
| \( y=\cos x \) | \( 0≦ x≦ \pi \) | \( -1≦ y≦ 1 \) |
| \( y=\tan x \) | \( -\frac{\pi}{2}<x<\frac{\pi}{2} \) | 実数全体 |
| \( y=\sin^{-1}x \) | \( -1≦ x≦ 1 \) | \( -\frac{\pi}{2}≦ y≦ \frac{\pi}{2} \) |
| \( y=\cos^{-1}x \) | \( -1≦ x≦ 1 \) | \( 0≦ y≦ \pi \) |
| \( y=\tan^{-1}x \) | 実数全体 | \( -\frac{\pi}{2}<y<\frac{\pi}{2} \) |
逆余割関数・逆正割関数・逆余接関数
先ほど紹介した \( \csc x, \ \sec x, \ \cot x \) の逆関数をそれぞれ \( \csc^{-1}x, \ \sec^{-1}x, \ \cot^{-1}x \) もしくは \( \text{arccsc} \ x, \ \text{arcsec} \ x, \ \text{arccot} \ x \) と表します。
これらをそれぞれアークコセカント、アークセカント、アークコタンジェントもしくは逆余割関数、逆正割関数、逆余接関数と呼びます。
\( \csc x, \ \sec x, \ \cot x \) も逆関数を考える場合には適切に定義域を制限する必要があります。
逆関数を考える際のそれぞれの関数の定義域と値域を表にまとめておきます。
| 関数 | 定義域 | 値域 |
| \( y=\csc x \) | \( -\frac{\pi}{2}≦ x<0, \ 0<x≦ \frac{\pi}{2} \) | \( y≦ -1, \ y≧1 \) |
| \( y=\sec x \) | \( 0≦ x<\frac{\pi}{2}, \ \frac{\pi}{2}<x≦ \pi \) | \( y≦ -1, \ y≧1 \) |
| \( y=\cot x \) | \( 0<x<\pi \) | 実数全体 |
| \( y=\csc^{-1}x \) | \( x≦ -1, \ x≧1 \) | \( -\frac{\pi}{2}≦ y<0, \ 0<y≦ \frac{\pi}{2} \) |
| \( y=\sec^{-1}x \) | \( x≦ -1, \ x≧1 \) | \( 0≦ y<\frac{\pi}{2}, \ \frac{\pi}{2}<y≦ \pi \) |
| \( y=\cot^{-1}x \) | 実数全体 | \( 0<y<\pi \) |
また、グラフは次のようになります。
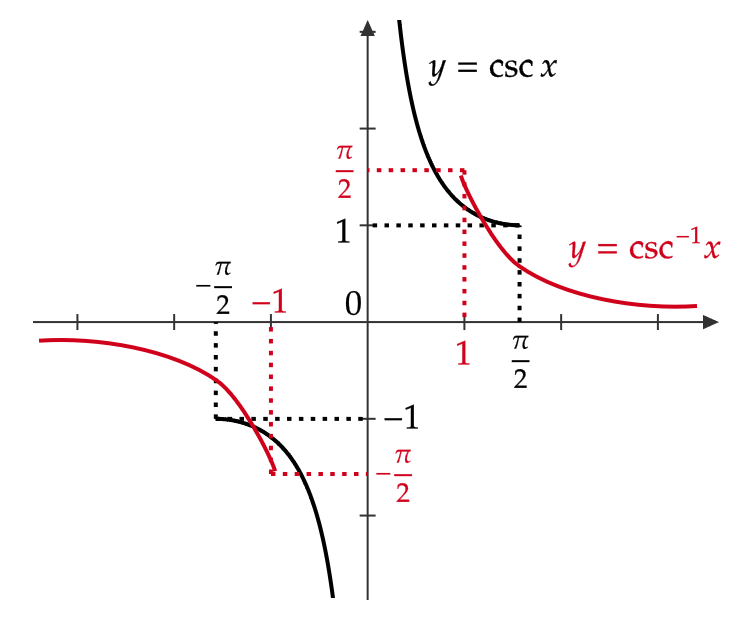
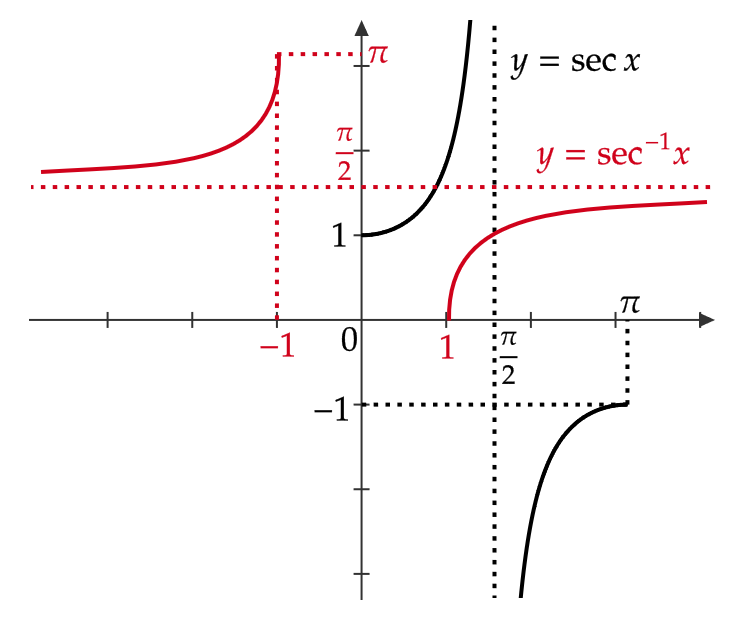
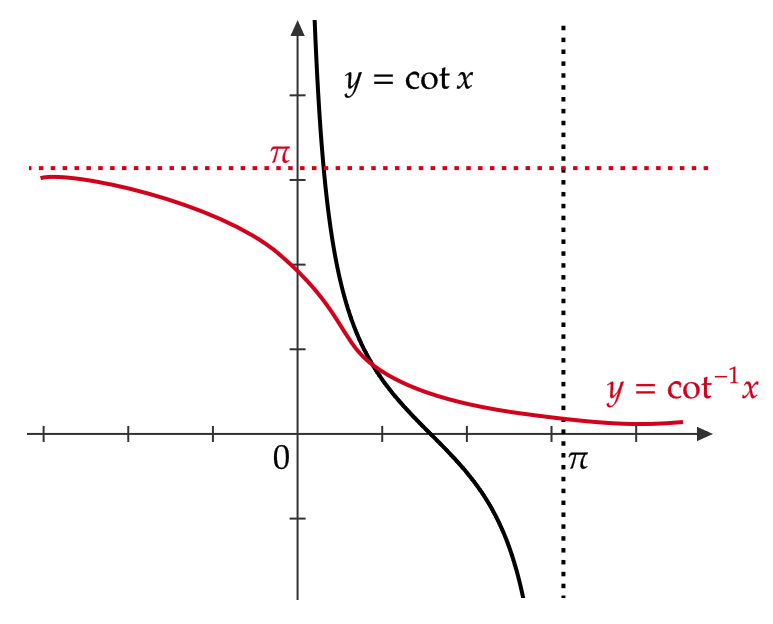
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

