こんにちは、ひかりです。
今回は線形代数学続論から置換・互換と置換の符号について解説していきます。
この記事では以下のことを紹介します。
- 置換の定義と積について
- 互換の定義と置換の互換による分解について
- 置換の符号について
置換の定義と積
線形代数学07で紹介した行列式の定義とは別の定義を考えたいと思います。
そのための準備として、この記事では置換について紹介します。
置換の定義
さっそく、置換を定義していきましょう。
集合 \( M_n \) を次で定める。
$$ M_n=\{1,2,\cdots,n \} $$
このとき、写像 \( \sigma:M_n\to M_n \) が全単射であるとき、 \( \sigma \) を \( M_n \) の置換という。
ここで、 \( M_n \) の各元に対する \( \sigma \) による対応が
$$ 1\mapsto i_1, \quad 2\mapsto i_2, \quad \cdots, \quad n\mapsto i_n $$
であるとき、 \( \sigma \) を次のように表す。
$$ \sigma=\begin{pmatrix} 1 & 2 & \cdots & n \\ i_1 & i_2 & \cdots & i_n \end{pmatrix} $$
さらに、集合 \( M_n \) の置換全体の集合を \( S_n \) と表す。
(1) \( S_2 \) は次の2つの置換から成る集合である。
$$ \begin{pmatrix} 1 & 2 \\ 1 & 2 \end{pmatrix}, \quad \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} $$
(例えば、 \( \begin{pmatrix} 1 & 2 \\ 1 & 1 \end{pmatrix} \) は写像 \( \sigma \) が全単射ではないので、置換ではない)
(2) \( S_3 \) は次の6つの置換から成る集合である。
$$ \begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}, \quad \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}, \quad \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} $$
$$ \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}, \quad \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}, \quad \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} $$
特別な置換に名前を付けておきましょう。
(1) (恒等置換)
写像 \( \sigma \) が恒等写像であるような置換
$$ \begin{pmatrix} 1 & 2 & \cdots & n \\ 1 & 2 & \cdots & n \end{pmatrix} $$
を恒等置換といい、 \( 1_n \) と表す。
(2) (逆置換)
写像 \( \sigma \) の逆写像から成る置換を逆置換といい、 \( \sigma^{-1} \) と表す。つまり、
$$ \sigma=\begin{pmatrix} 1 & 2 & \cdots & n \\ i_1 & i_2 & \cdots & i_n \end{pmatrix} \quad のとき \quad \sigma^{-1}=\begin{pmatrix} i_1 & i_2 & \cdots & i_n \\ 1 & 2 & \cdots & n \end{pmatrix} $$
置換
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$
の逆置換 \( \sigma^{-1} \) を求めると、
$$ \sigma^{-1}=\begin{pmatrix} 2 & 3 & 1 \\ 1 & 2 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} $$
置換の積
2つの置換の積を次で定義します。
2つの置換 \( \sigma,\tau\in S_n \) に対して、合成写像
$$ \tau \circ \sigma:M_n\to M_n $$
を置換 \( \sigma,\tau \) の積といい、 \( \tau\sigma \) と表す。これにより置換
$$ \sigma=\begin{pmatrix} 1 & 2 & \cdots & n \\ i_1 & i_2 & \cdots & i_n \end{pmatrix}, \quad \tau=\begin{pmatrix} i_1 & i_2 & \cdots & i_n \\ j_1 & j_2 & \cdots & j_n \end{pmatrix} $$
に対して、
$$ \tau\sigma=\begin{pmatrix} i_1 & i_2 & \cdots & i_n \\ j_1 & j_2 & \cdots & j_n \end{pmatrix}\begin{pmatrix} 1 & 2 & \cdots & n \\ i_1 & i_2 & \cdots & i_n \end{pmatrix}=\begin{pmatrix} 1 & 2 & \cdots & n \\ j_1 & j_2 & \cdots & j_n \end{pmatrix} $$
と考えることができる。
2つの置換
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}, \quad \tau=\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} $$
に対して、積 \( \tau\sigma \) と \( \sigma\tau \) を求める。
$$ \begin{align} \tau\sigma&=\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} \\ &=\begin{pmatrix} 2 & 3 & 1 \\ 3 & 2 & 1 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix} \end{align} $$
$$ \begin{align} \sigma\tau&=\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} \\ &=\begin{pmatrix} 1 & 3 & 2 \\ 2 & 1 & 3 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} \end{align} $$
よって、一般に \( \tau\sigma \) と \( \sigma\tau \) は一致しない。
置換の積に関して次のことが成り立ちます。
(1) (結合法則) 任意の \( \sigma,\tau,\rho\in S_n \) に対して、
$$ (\rho\tau)\sigma=\rho(\tau\sigma) $$
(2) (単位元の存在) 任意の \( \sigma\in S_n \) に対して、
$$ \sigma 1_n=1_n\sigma=\sigma $$
(3) (逆元の存在) 任意の \( \sigma\in S_n \) に対して、
$$ \sigma^{-1}\sigma=\sigma\sigma^{-1}=1_n $$
定理1の証明(気になる方だけクリックしてください)
表記を簡単にするために \( S_3 \) で示します。
(1) 任意の \( \sigma,\tau,\rho\in S_3 \) を次のように表します。
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix}, \quad \tau=\begin{pmatrix} 1 & 2 & 3 \\ \tau(1) & \tau(2) & \tau(3) \end{pmatrix}, $$
$$ \rho=\begin{pmatrix} 1 & 2 & 3 \\ \rho(1) & \rho(2) & \rho(3) \end{pmatrix} $$
このとき、
$$ \begin{align} &(\rho\tau)\sigma \\ &=\left( \begin{pmatrix} 1 & 2 & 3 \\ \rho(1) & \rho(2) & \rho(3) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \tau(1) & \tau(2) & \tau(3) \end{pmatrix} \right) \begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} \\ &=\left( \begin{pmatrix} \tau(1) & \tau(2) & \tau(3) \\ \tau(\rho(1)) & \tau(\rho(2)) & \tau(\rho(3)) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \tau(1) & \tau(2) & \tau(3) \end{pmatrix} \right) \begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 & 3 \\ \tau(\rho(1)) & \tau(\rho(2)) & \tau(\rho(3)) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} \\ &=\begin{pmatrix} \sigma(1) & \sigma(2) & \sigma(3) \\ \sigma(\tau(\rho(1))) & \sigma(\tau(\rho(2))) & \sigma(\tau(\rho(3))) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 & 3 \\ \sigma(\tau(\rho(1))) & \sigma(\tau(\rho(2))) & \sigma(\tau(\rho(3))) \end{pmatrix} \\ &=\begin{pmatrix} \sigma(\tau(1)) & \sigma(\tau(2)) & \sigma(\tau(3)) \\ \sigma(\tau(\rho(1))) & \sigma(\tau(\rho(2))) & \sigma(\tau(\rho(3))) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \sigma(\tau(1)) & \sigma(\tau(2)) & \sigma(\tau(3)) \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 & 3 \\ \rho(1) & \rho(2) & \rho(3) \end{pmatrix}\left(\begin{pmatrix} \sigma(1) & \sigma(2) & \sigma(3) \\ \sigma(\tau(1)) & \sigma(\tau(2)) & \sigma(\tau(3)) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix}\right) \\ &=\begin{pmatrix} 1 & 2 & 3 \\ \rho(1) & \rho(2) & \rho(3) \end{pmatrix}\left(\begin{pmatrix} 1 & 2 & 3 \\ \tau(1) & \tau(2) & \tau(3) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix}\right) \\ &=\rho(\tau\sigma) \end{align} $$
(2) 任意の \( \sigma\in S_3 \) を次のように表します。
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} $$
このとき、
$$ \begin{align} \sigma 1_3&=\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix}=\sigma \end{align} $$
$$ \begin{align} 1_3\sigma&=\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} \\ &=\begin{pmatrix} \sigma(1) & \sigma(2) & \sigma(3) \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix}=\sigma \end{align} $$
よって、
$$ \sigma 1_3=1_3\sigma=\sigma $$
(3) 任意の \( \sigma\in S_3 \) を次のように表します。
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} $$
このとき、 \( \sigma \) の逆置換を \( \sigma^{-1} \) とおくと、
$$ \begin{align} \sigma^{-1}\sigma&=\begin{pmatrix} \sigma(1) & \sigma(2) & \sigma(3) \\ 1 & 2 & 3 \end{pmatrix}\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}=1_3 \end{align} $$
$$ \begin{align} \sigma\sigma^{-1}&=\begin{pmatrix} 1 & 2 & 3 \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix}\begin{pmatrix} \sigma(1) & \sigma(2) & \sigma(3) \\ 1 & 2 & 3 \end{pmatrix} \\ &=\begin{pmatrix} \sigma(1) & \sigma(2) & \sigma(3) \\ \sigma(1) & \sigma(2) & \sigma(3) \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}=1_3 \end{align} $$
よって、
$$ \sigma^{-1}\sigma=\sigma\sigma^{-1}=1_3 $$
定理1により、 \( M_n \) は群とよばれているものとなります。
とくに、 \( M_n \) は対称群や置換群といいます。
互換の定義と置換の互換による分解
互換の定義
まず、互換の定義に必要な巡回置換について定義します。
集合 \( M_n \) のうち、 \( i_1,i_2,\cdots,i_m \) 以外を動かさず、 \( i_1,i_2,\cdots,i_m \) のみが
$$ i_1 \to i_2, \quad i_2 \to i_3, \quad \cdots, \quad i_m\to i_1 $$
と巡回するように移るような置換
$$ \sigma=\begin{pmatrix} i_1 & i_2 & \cdots & i_m & i_{m+1} & \cdots & i_n \\ i_2 & i_3 & \cdots & i_1 & i_{m+1} & \cdots & i_n \end{pmatrix} $$
を巡回置換といい、
$$ \sigma=\begin{pmatrix} i_1 & i_2 & \cdots & i_m \end{pmatrix} $$
と表す。
置換
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 4 & 2 & 5 & 3 & 1 & 6 \end{pmatrix} $$
は、次のように書き換えられる。
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 4 & 2 & 5 & 3 & 1 & 6 \end{pmatrix}=\begin{pmatrix} 1 & 4 & 3 & 5 & 2 & 6 \\ 4 & 3 & 5 & 1 & 2 & 6 \end{pmatrix} $$
よって、 \( \sigma \) は巡回置換であり、
$$ \sigma=\begin{pmatrix} 1 & 4 & 3 & 5 \end{pmatrix} $$
と表される。
それでは、互換を定義していきましょう。
2つの文字 \( i \) と \( j \) のみ入れ替えた置換、つまり2文字の巡回置換 \( \begin{pmatrix} i & j \end{pmatrix} \) を互換という。
置換の互換による分解
互換というのは2文字の入れ替えのみの置換となるので、とても扱いやすいです。
なので、任意の置換を互換の積で表現できないかということを考えます。
まずはじめに次の定理を示します。
任意の置換は同じ文字を含まない巡回置換の積で表すことができ、その表し方は積の順序を除いて1通りである。
定理2の証明(気になる方だけクリックしてください)
任意に置換 \( \sigma \) を与えます。
$$ \sigma=\begin{pmatrix} 1 & 2 & \cdots & n \\ i_1 & i_2 & \cdots & i_n \end{pmatrix} $$
ここで、 \( 1 \) が次のように移っていくとします。
$$ 1\to j_1 \to j_2 \to j_3 \to \cdots $$
このとき、この移り変わりは \( M_n \) の部分集合を回って \( 1 \) に帰ってくることを示します。
もし \( 1 \) に帰ってこないと仮定すると、 \( M_n \) は有限集合なのでいつかは \( 1 \) 以外の一度移った文字に再び移ることになります。
そのはじめての文字を \( j_k \) とおきます。
そして、 \( j_m \to j_k \) になるとします。
このとき、図のようになります。
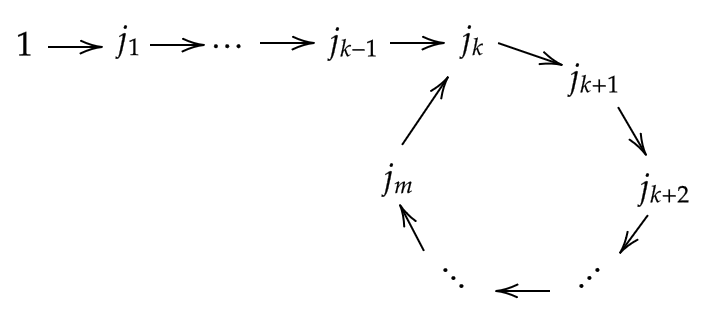
ここで、
$$ j_{k-1}\to j_k, \quad j_m\to j_k $$
となるが、これは写像 \( \sigma \) が単射であることに反します。
( \( j_{k-1}\not=j_m \) より、単射であるならば \( \sigma(j_{k-1})\not=\sigma(j_m) \) でなければならない)
よって、 \( \sigma \) が置換であることに矛盾します。
したがって、 \( 1 \) をスタートとする移り変わりは必ず \( 1 \) に帰ってきます。つまり、
$$ 1\to j_1 \to j_2 \to j_3 \to \cdots \to j_{k-1} \to 1 $$
よって、これは巡回置換
$$ \begin{pmatrix} 1 & j_1 & j_2 & \cdots & j_{k-1} \end{pmatrix} $$
で表されます。
次に、 \( 1,j_1,j_2,\cdots,j_{k-1} \) 以外の文字をスタートにして同じようなことを考えると、別の巡回置換が出てきます。
これを繰り返すことにより、任意の置換は巡回置換の積で表されます。
( \( M_n \) は有限集合なので、この操作は有限回で終わります。)
次の置換を考える。
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ 2 & 4 & 7 & 8 & 1 & 9 & 3 & 6 & 5 \end{pmatrix} $$
これは次の2つの移り方で表される。
$$ 1 \to 2 \to 4 \to 8 \to 6 \to 9 \to 5 \to 1 $$
$$ 3 \to 7 \to 3 $$
よって、 \( \sigma \) は次の2つの巡回置換の積で表される。
$$ \sigma=\begin{pmatrix} 1 & 2 & 4 & 8 & 6 & 9 & 5 \end{pmatrix}\begin{pmatrix} 3 & 7 \end{pmatrix} $$
また、次の定理も成り立ちます。
巡回置換 \( \begin{pmatrix} i_1 & i_2 & \cdots & i_m \end{pmatrix} \) は次のように \( m-1 \) 個の互換の積に表される。
$$ \begin{pmatrix} i_1 & i_2 & \cdots & i_m \end{pmatrix}=\begin{pmatrix} i_1 & i_m \end{pmatrix}\begin{pmatrix} i_1 & i_{m-1} \end{pmatrix}\cdots\begin{pmatrix} i_1 & i_3 \end{pmatrix}\begin{pmatrix} i_1 & i_2 \end{pmatrix} $$
定理3の証明(気になる方だけクリックしてください)
実際に上の表し方を計算してみればわかります。
例えば \( m=3 \) で計算してみましょう。
$$ \begin{align} \begin{pmatrix} i_1 & i_3 \end{pmatrix}\begin{pmatrix} i_1 & i_2 \end{pmatrix}&=\begin{pmatrix} i_1 & i_3 & i_2 & i_4 & \cdots & i_n \\ i_3 & i_1 & i_2 & i_ 4 & \cdots & i_n \end{pmatrix}\begin{pmatrix} i_1 & i_2 & i_3 & i_4 & \cdots & i_n \\ i_2 & i_1 & i_3 & i_ 4 & \cdots & i_n \end{pmatrix} \\ &=\begin{pmatrix} i_1 & i_2 & i_3 & i_4 & \cdots & i_n \\ i_2 & i_3 & i_1 & i_ 4 & \cdots & i_n \end{pmatrix} \\ &=\begin{pmatrix} i_1 & i_2 & i_3 \end{pmatrix} \end{align} $$
巡回置換
$$ \begin{pmatrix} 1 & 2 & 4 & 8 & 6 & 9 & 5 \end{pmatrix} $$
は定理3より、次のように \( 6 \) 個の互換の積に表される。
$$ \begin{pmatrix} 1 & 2 \end{pmatrix}\begin{pmatrix} 1 & 4 \end{pmatrix}\begin{pmatrix} 1 & 8 \end{pmatrix}\begin{pmatrix} 1 & 6 \end{pmatrix}\begin{pmatrix} 1 & 9 \end{pmatrix}\begin{pmatrix} 1 & 5 \end{pmatrix} $$
定理2と定理3を組み合わせることによって、求めたい定理が得られました。
任意の置換は互換の積で表される。
次の置換を考える。
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ 2 & 4 & 7 & 8 & 1 & 9 & 3 & 6 & 5 \end{pmatrix} $$
例5と例6を組み合わせることによって、
$$ \begin{align} \sigma&=\begin{pmatrix} 1 & 2 & 4 & 8 & 6 & 9 & 5 \end{pmatrix}\begin{pmatrix} 3 & 7 \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 \end{pmatrix}\begin{pmatrix} 1 & 4 \end{pmatrix}\begin{pmatrix} 1 & 8 \end{pmatrix}\begin{pmatrix} 1 & 6 \end{pmatrix}\begin{pmatrix} 1 & 9 \end{pmatrix}\begin{pmatrix} 1 & 5 \end{pmatrix}\begin{pmatrix} 3 & 7 \end{pmatrix} \end{align} $$
と \( 7 \) 個の互換の積に分解することができる。
置換の符号
定理4より、置換の符号を次のように定めることができます。
置換 \( \sigma \) に対して、 \( \sigma \) を互換の積に分解したときの互換の個数 \( m \) を用いて、置換 \( \sigma \) の符号 \( \text{sgn} \ \sigma \) を次で定める。
$$ \text{sgn} \ \sigma=(-1)^m $$
ただし、このままでは大きな問題があります。
それは、互換の積の表し方は一通りではなく、しかも個数も変わる場合があることです。
置換
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} $$
は次のように互換の積に分解できる。
$$ \begin{align} \sigma&=\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 \end{pmatrix}\begin{pmatrix} 1 & 3 \end{pmatrix} \\ &=\begin{pmatrix} 1 & 2 \end{pmatrix}\begin{pmatrix} 1 & 3 \end{pmatrix}\begin{pmatrix} 3 & 1 \end{pmatrix}\begin{pmatrix} 1 & 3 \end{pmatrix} \end{align} $$
しかし、ここでポイントとなるのは個数は変わっても偶数個か奇数個かは変わらないということです。
(つまり、互換の積に分解したときに互換の個数が偶数個であったならば、ほかにどんな互換の積の表し方があったとしても互換の個数はつねに偶数個であり、符号は \( 1 \) となります。)
よって、置換の符号はどの置換に対しても、必ず定まります。
まとめると、
任意の置換 \( \sigma \) を互換の積に分解するときに、その互換の個数が偶数個か奇数個かは与えられた置換 \( \sigma \) によってのみ定まり、互換の積の表し方によらない。
定理6より、次を定義できます。
偶数個の互換の積で表される置換を偶置換、奇数個の互換の積で表される置換を奇置換という。
このとき、置換 \( \sigma \) の符号 \( \text{sgn} \ \sigma \) は次のように表すことができる。
$$ \text{sgn} \ \sigma=\begin{cases} +1 & (偶置換のとき) \\ -1 & (奇置換のとき) \end{cases} $$
次の置換を考える。
$$ \sigma=\begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 4 & 1 & 3 \end{pmatrix} $$
これは次のように互換の積に分解できます。
$$ \begin{align} \sigma&=\begin{pmatrix} 1 & 2 & 3 & 4 \\ 2 & 4 & 1 & 3 \end{pmatrix} \\ &=\begin{pmatrix} 1 & 3 \end{pmatrix}\begin{pmatrix} 1 & 4 \end{pmatrix}\begin{pmatrix} 1 & 2 \end{pmatrix} \end{align} $$
よって、置換 \( \sigma \) の符号は
$$ \text{sgn} \ \sigma=(-1)^3=-1 $$
最後に置換の符号の性質について紹介します。
任意の \( \sigma,\tau\in S_n \) に対して次が成り立つ。
(1) $$ \text{sgn} \ (\tau\sigma)=\text{sgn} \ (\tau) \ \text{sgn} \ (\sigma) $$
(2) $$ \text{sgn} \ (1_n)=1 $$
(3) $$ \text{sgn} \ (\sigma^{-1})=\text{sgn} \ (\sigma) $$
定理6の証明(気になる方だけクリックしてください)
(1) 任意に置換 \( \sigma,\tau\in S_n \) をとると、定理4より互換の積で表すことができます。
これを次のように表します。
$$ \sigma=\sigma_{\ell}\sigma_{\ell-1}\cdots\sigma_1, \quad \tau=\tau_m\tau_{m-1}\cdots \tau_1 $$
このとき、積 \( \tau\sigma \) は次のように互換の積で表せます。
$$ \tau\sigma=\tau_m\tau_{m-1}\cdots \tau_1\sigma_{\ell}\sigma_{\ell-1}\cdots\sigma_1 $$
よって、
$$ \text{sgn} \ (\tau\sigma)=(-1)^{m+\ell}=(-1)^m(-1)^{\ell}=\text{sgn} \ (\tau) \ \text{sgn} \ (\sigma) $$
(2) 置換 \( 1_n \) は無理やり2個の置換で表せます。
$$ 1_n=\begin{pmatrix} 1 & 2 \end{pmatrix}\begin{pmatrix} 2 & 1 \end{pmatrix} $$
よって、
$$ \text{sgn} \ (1_n)=(-1)^2=1 $$
(3) 置換 \( \sigma \) に対して、逆置換 \( \sigma^{-1} \) を考えると、定理1の(3)より、
$$ \sigma^{-1}\sigma=\sigma\sigma^{-1}=1_n $$
よって、(1)と(2)より、
$$ \text{sgn} \ (\sigma^{-1}) \ \text{sgn} \ (\sigma)=\text{sgn} \ (\sigma^{-1}\sigma)=\text{sgn} \ (1_n)=1 $$
したがって、 \( \text{sgn} \ (\sigma) \) は \( 1 \) か \( -1 \) しかとらないことに注意すると、
$$ \text{sgn} \ (\sigma^{-1})=\frac{1}{\text{sgn} \ (\sigma)}=\text{sgn} \ (\sigma) $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

