こんにちは、ひかりです。
今回は線形代数学続論から写像の全射・単射と数ベクトル空間について解説していきます。
この記事では以下のことを紹介します。
- 写像の定義と全射・単射について
- 写像の合成と逆像・逆写像について
- 数ベクトル空間について
写像の定義と全射・単射
関数と写像
関数とは、一つの実数 \( x \) に対して、一つの実数 \( f(x) \) を返す規則 \( f \) のことをいいました。
これを拡張した概念として写像を定義します。
2つの集合 \( X,Y \) があるとき、集合 \( X \) の1つの元に対して、集合 \( Y \) の1つの元を返す規則 \( f \) のことを写像といい、
$$ f:X\to Y $$
と表す。このとき、 \( X \) を写像 \( f \) の定義域、 \( Y \) を写像 \( f \) の終域という。
また、 \( X \) の元 \( x \) に対して \( Y \) の元 \( y \) が対応するとき、
$$ y=f(x) $$
と表す。
さらに、 \( x \) が \( X \) のすべての元をわたるときの値 \( f(x) \) 全体のつくる \( Y \) の部分集合を、写像 \( f \) の像(値域)といい、 \( \text{Im} f \) または \( f(X) \) で表す。つまり、
$$ \text{Im}f=f(X)=\{ f(x) \ | \ x\in X \} $$
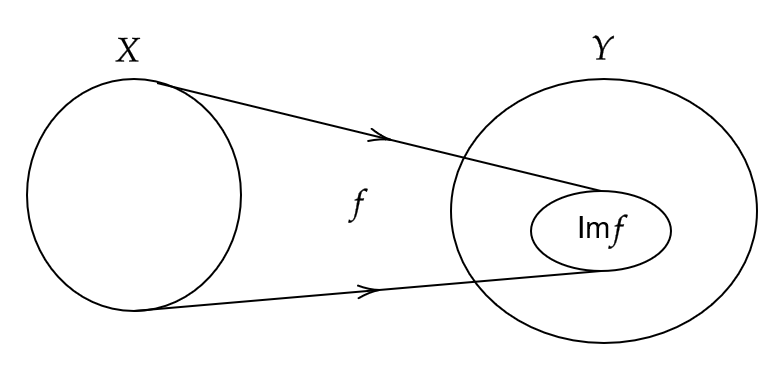
(1) 関数は写像であるので、
$$ f(x)=3x, \quad g(x)=x^2, \quad h(x)=\sin x $$
などはすべて写像である。
また、定義域を \( \mathbb{R} \) (実数全体)としたときの、像 \( \text{Im} \) はそれぞれ、
$$ \text{Im}f=\mathbb{R}, \quad \text{Im}g=\{ y \ | \ y≧0 \}, \quad \text{Im}h=\{ y \ | \ -1≦y≦1 \} $$
(2) 集合 \( X,Y \) を次で定める。
$$ X=\{ a,b,c \}, \quad Y=\{ d,e,f,g \} $$
このとき、
$$ f(a)=e, \ f(b)=g, \ f(c)=e $$
と定めた規則 \( f \) は写像である。
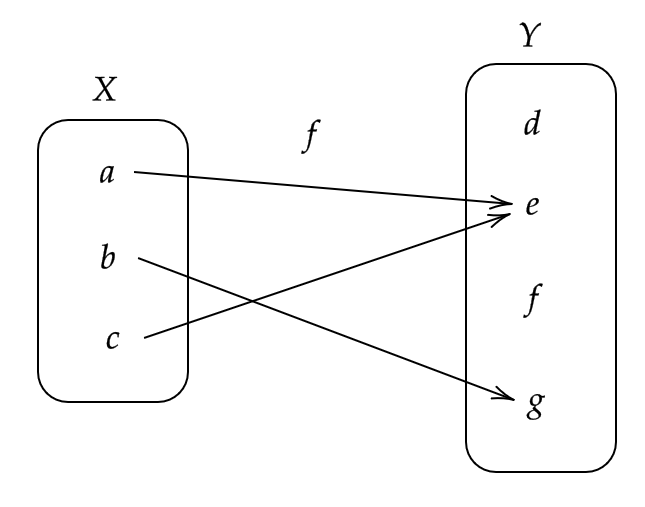
また、像 \( \text{Im} f \) は
$$ \text{Im} f=\{ e,g \} $$
最後に、特別な写像を1つ紹介します。
定義域も値域も同じ集合 \( X \) である写像 \( f:X\to X \) であって、 \( X \) の任意の元 \( x \) に対して、同じ元 \( x \) を対応する写像を恒等写像といい、
$$ \text{id}:X\to X $$
と表す。
写像の全射・単射
次に写像の重要な概念である全射性と単射性について紹介します。
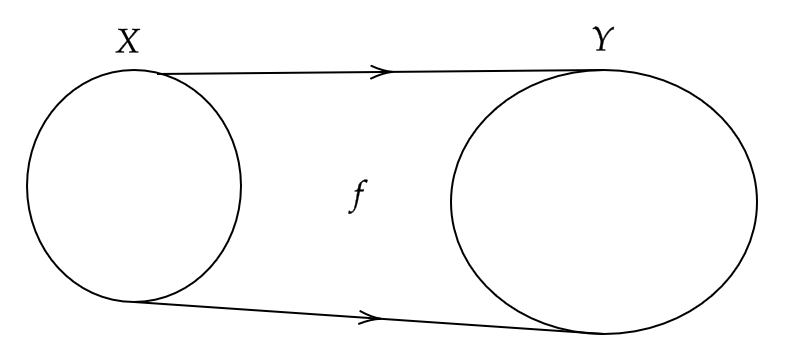
(1) 一般に写像 \( f \) の像 \( \text{Im} f \) は \( Y \) の部分集合であり一致するとは限らないが、もし一致するとき、つまり
$$ \text{Im} f=Y $$
となるとき、 \( f \) は全射であるという。
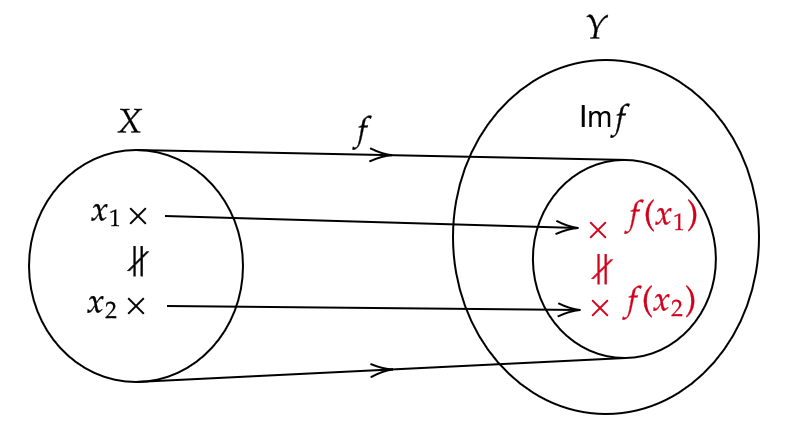
(2) \( X \) の任意の2点 \( x_1, x_2 \) が異なる点であるとき、 \( f(x_1)\not=f(x_2) \) が成り立つとき、 \( f \) は単射であるという。
(対偶をとると、 \( f(x_1)=f(x_2) \) ならば \( x_1=x_2 \) が成り立つとき、 \( f \) は単射である。)
(3) \( f \) が全射かつ単射であるとき、全単射であるという。
(1) 次の \( \mathbb{R} \) から \( \mathbb{R} \) への写像を考える。
$$ f_1(x)=2x+3 $$
これは全単射であることを示す。まず、 \( f_1 \) の像 \( \text{Im} f_1 \) を考えると、
$$ \text{Im} f_1=\mathbb{R} $$
であるので、 \( f_1 \) は全射である。
また、 \( x_1\not=x_2 \) とすると、
$$ 2x_1+3\not=2x_2+3 $$
であるので、 \( f_1 \) は単射である。したがって、 \( f_1 \) は全単射である。
(2) 次の \( \mathbb{R} \) から \( \mathbb{R} \) への写像を考える。
$$ f_2(x)=x^3-x $$
これは全射であるが単射ではないことを示す。
まず、 \( f_2 \) の像 \( \text{Im} f_2 \) を考えると、
$$ \text{Im} f_2=\mathbb{R} $$
であるので、 \( f_2 \) は全射である。
しかし、 \( x_1=1, \ x_2=-1 \) とおくと、 \( x_1\not=x_2 \) ではあるが、
$$ x_1^3-x_1=1^3-1=0, \quad x_2^3-x_2=(-1)^3-(-1)=(-1)+1=0 $$
より、 \( f_2(x_1)=f_2(x_2) \) となるので、 \( f_2 \) は単射ではない。
(3) 次の \( \mathbb{R} \) から \( \mathbb{R} \) への写像を考える。
$$ f_3(x)=2^x $$
これは単射であるが全射ではないことを示す。
まず、 \( f_3 \) の像 \( \text{Im} f_3 \) を考えると、
$$ \text{Im} f_3=\{ y \ | \ y>0 \} $$
であるので、 \( f_3 \) は全射ではない。
また、 \( x_1\not=x_2 \) とすると、
$$ 2^{x_1}\not=2^{x_2} $$
であるので、 \( f_3 \) は単射である。
(4) 次の \( \mathbb{R} \) から \( \mathbb{R} \) への写像を考える。
$$ f_4(x)=x^2 $$
これは全射でも単射でもないことを示す。
まず、 \( f_4 \) の像 \( \text{Im} f_4 \) を考えると、
$$ \text{Im} f_4=\{ y \ | \ y≧0 \} $$
であるので、 \( f_4 \) は全射ではない。
また、 \( x_1=1, \ x_2=-1 \) とおくと、 \( x_1\not=x_2 \) ではあるが、
$$ x_1^2=1^2=1, \quad x_2^2=(-1)^2=1 $$
より、 \( f_4(x_1)=f_4(x_2) \) となるので、 \( f_4 \) は単射ではない。
写像の合成と逆像・逆写像
合成写像
関数の場合も合成関数という概念があったように、写像に対しても合成写像という概念が定義されます。
2つの写像
$$ f:X\to Y, \quad g:Y\to Z $$
を考えます。このとき、 \( X \) の元 \( x \) は \( f \) によって、 \( Y \) の元 \( y=f(x) \) に移ります。
さらに、 \( Y \) の元 \( y \) は \( g \) によって、 \( Z \) の元 \( z=g(y) \) に移ります。
よって、 \( X \) の元 \( x \) に対して、 \( Z \) の元 \( z=g(f(x)) \) に移るような写像が考えられます。
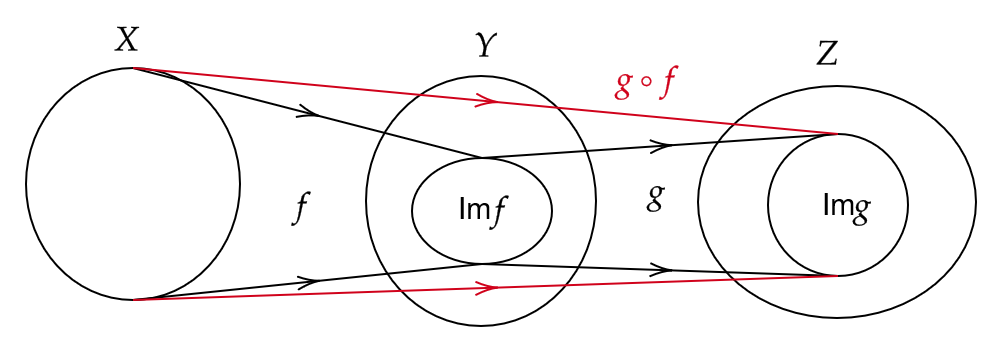
これを \( f \) と \( g \) の合成写像とよびます。
まとめると、
2つの写像
$$ f:X\to Y, \quad g:Y\to Z $$
を考える。このとき、 \( X \) の元 \( x \) に対して、 \( Z \) の元 \( z=g(f(x)) \) に移る写像を \( f \) と \( g \) の合成写像といい、 \( g\circ f \) と表す。つまり、
$$ g\circ f:X\to Z $$
(1) 次の2つの写像を考える。
$$ f(x)=x^2+1, \quad g(y)=\log y $$
ただし、 \( f \) は \( \mathbb{R} \) から \( \{ y \ | \ y>0 \} \) の写像、 \( g \) は \( \{ y \ | \ y>0 \} \) から \( \mathbb{R} \) の写像として考える。
このとき、 \( f \) の終域と \( g \) の定義域が等しいので、 \( g\circ f \) を考えることができて、
$$ g\circ f(x)=g(f(x))=\log (x^2+1) $$
(2) 次の2つの写像を考える。
$$ f(x)=a, \quad g(y)=b \quad (a,b:定数) $$
ただし、 \( f, \ g \) は \( \mathbb{R} \) から \( \mathbb{R} \) の写像として考える。
(このような \( f, \ g \) のことを定値写像(定数関数)という。)
このとき、 \( g\circ f \) と \( f\circ g \) はともに存在するが、
$$ g\circ f(x)=g(f(x))=b, \quad f\circ g(y)=f(g(y))=a $$
となるので、 \( g\circ f\not=f\circ g \) である。
また、全単射性と合成写像の関係として次が成り立ちます。
次の2つの写像を考える。
$$ f:X\to Y, \quad g:Y\to Z $$
(1) 写像 \( f,g \) がともに全射であるならば、合成写像 \( g\circ f \) も全射である。
(2) 写像 \( f,g \) がともに単射であるならば、合成写像 \( g\circ f \) も単射である。
(3) 写像 \( f,g \) がともに全単射であるならば、合成写像 \( g\circ f \) も全単射である。
定理1の証明(気になる方だけクリックしてください)
(1) まず、 \( g \) が全射であることから、 \( \text{Im}g=Z \) となります。
これはつまり、 \( Z \) から任意に元 \( z \) をとったときに \( g(y)=z \) となる \( y\in Y \) が(複数個あるかもしれないが)必ず存在するということになります。
(ないのであれば、その \( z \) は \( \text{Im}g \) には属さないからです。)
同様に、 \( f \) が全射であることから、いま存在することがわかった \( y\in Y \) に対して、 \( f(x)=y \) となる \( x\in X \) が(複数個あるかもしれないが)必ず存在するということになります。
したがって、任意の \( z\in Z \) に対して、
$$ z=g(y)=g(f(x))=(g\circ f )(x) $$
となる \( x\in X \) が存在することがわかったので、 \( g\circ f \) も全射となります。
(2) \( g\circ f \) が単射であることを示すために、
$$ (g\circ f)(x_1)= (g\circ f)(x_2) $$
を仮定します。このとき、
$$ g(f(x_1))=g(f(x_2)) $$
であるので、 \( g \) の単射性より、
$$ f(x_1)=f(x_2) $$
となります。同様に、 \( f \) の単射性より、
$$ x_1=x_2 $$
したがって、単射性の定義(正確にはその対偶)より、 \( g\circ f \) も単射となります。
(3) (1)と(2)を合わせれば成り立ちます。
写像の逆像と逆写像
次に、逆関数の写像版である逆像と逆写像について紹介します。
写像 \( f:X\to Y \) と \( Y \) の部分集合 \( Q \) を与える。
このとき、 \( Q \) の元 \( y \) に対して、 \( f(x)=y \) となる \( X \) の元 \( x \) が存在するとき、その \( x \) を \( f \) の \( y \) における逆像という。
また、 \( y \) が \( Q \) のすべての元をわたるときの \( y \) における逆像 \( x \) 全体の集合を \( f \) の \( Q \) における逆像といい、 \( f^{-1}(Q) \) と表す。
例1の(2)の写像を考える。

このとき、 \( Y \) の部分集合 \( Q_1, \ Q_2, \ Q_3 \) を次で与える。
$$ Q_1=\{ d,e \}, \quad Q_2=\{ e,f,g \}, \quad Q_3=\{d,f \} $$
ここで、
$$ f(a)=f(c)=e, \quad f(b)=g, \quad d,fは逆像をもたない $$
よって、 \( Q_1, \ Q_2, \ Q_3 \) の逆像 \( f^{-1}(Q_1), \ f^{-1}(Q_2), \ f^{-1}(Q_3) \) は次のようになる。
$$ f^{-1}(Q_1)=\{ a,c \}, \quad f^{-1}(Q_2)=X, \quad f^{-1}(Q_3)=\emptyset $$
次に、逆写像を考えるうえで重要な定理を紹介します。
写像 \( f:X\to Y \) が全単射であるならば、写像 \( g:Y\to X \) が存在して、次をみたす。
$$ g\circ f=\text{id}, \quad f\circ g=\text{id} $$
定理2の証明(気になる方だけクリックしてください)
まず、 \( f \) が全射であることから、 \( Y \) から任意に元 \( y \) をとったときに \( f(x)=y \) となる \( x \) が(複数個あるかもしれないが)必ず存在するということになります。
(理由は定理1の証明と同じです)
さらに、 \( f \) が単射であるので、この \( x \) はただ1つであることがいえます。
なぜなら、もし \( x_1,x_2 \) の2つ存在したとすると、
$$ f(x_1)=f(x_2)=y $$
となるわけですが、 \( f \) の単射性の定義(正確にはその対偶)より、
$$ x_1=x_2 $$
となるので、ただ1つしか存在しません。
したがって、各 \( y \) に対して、 \( x \) がただ一つ定めるような規則ができたので、それを写像 \( g:Y\to X \) と定めます。つまり、 \( x=g(y) \) となります。
さらに、 \( g\circ f \) と \( f\circ g \) を計算してみると、
$$ g\circ f(x)=g(f(x))=g(y)=x $$
$$ f\circ g(y)=f(g(y))=f(x)=y $$
よって、
$$ g\circ f=\text{id}, \quad f\circ g=\text{id} $$
定理2をみたす写像 \( g:Y\to X \) のことを、写像 \( f:X\to Y \) の逆写像といい、 \( g=f^{-1} \) と書く。つまり、
$$ f^{-1}\circ f=\text{id}, \quad f\circ f^{-1}=\text{id} $$
例2(1)で紹介した次の \( \mathbb{R} \) から \( \mathbb{R} \) への写像を考える。
$$ y=f(x)=2x+3 $$
これは例2(1)より、全単射である。
よって、逆写像 \( f^{-1} \) が存在して、それは
$$ f^{-1}(y)=\frac{y-3}{2} $$
実際、 \( f^{-1}\circ f \) と \( f\circ f^{-1} \) を計算してみると、
$$ f^{-1}\circ f(x)=f^{-1}(f(x))=f^{-1}(2x+3)=\frac{(2x+3)-3}{2}=x $$
$$ f\circ f^{-1}(y)=f(f^{-1}(y))=f(\frac{y-3}{2})=2\cdot \frac{y-3}{2}+3=y $$
より、
$$ f^{-1}\circ f=\text{id}, \quad f\circ f^{-1}=\text{id} $$
最後に、定理2の逆ともいえる次の定理を紹介します。
2つの写像
$$ f:X\to Y, \quad g:Y\to X $$
が
$$ g\circ f=\text{id} $$
をみたすならば、 \( f \) は単射、 \( g \) は全射である。
さらに、
$$ f\circ g=\text{id} $$
もみたすならば、 \( f,g \) はともに全単射であり、
$$ f^{-1}=g, \quad g^{-1}=f $$
定理3の証明(気になる方だけクリックしてください)
まず、 \( g\circ f=\text{id} \) をみたすとき、 \( f \) は単射、 \( g \) は全射であることを示します。
まず、 \( f \) が単射であることを示すために、 \( f(x_1)=f(x_2) \) であるとします。
このとき、 \( x_1=x_2 \) となることを示します。
\( f(x_1), f(x_2) \) をそれぞれ \( g \) で移すと、 \( g\circ f=\text{id} \) より、
$$ g(f(x_1))=g\circ f(x_1)=\text{id}(x_1)=x_1 $$
$$ g(f(x_2))=g\circ f(x_2)=\text{id}(x_2)=x_2 $$
ここで、 \( f(x_1)=f(x_2) \) に注意すると、 \( g \) は写像であるので写像の定義より、
$$ g(f(x_1))=g(f(x_2)) $$
となります。
(もし、等しくなければ、1つの元に対して2つの元を返すことになるので写像になりません)
まとめると、 \( x_1=x_2 \) となるので、 \( f \) は単射となります。
次に、 \( g \) が全射であることを示すために、 \( g \) の終域 \( X \) から任意に元 \( x \) をとります。
このとき、 \( g(y)=x \) となる \( y\in Y \) が存在することを示します。
定理の仮定より、
$$ g(f(x))=g\circ f(x)=\text{id}(x)=x $$
であるので、 \( f(x)\in Y \) より、 \( y=f(x) \) とすれば、 \( g(y)=x \) をみたします。
したがって、 \( g \) は全射となります。
最後に、 \( f\circ g=\text{id} \) もみたすのであれば、先ほどの議論により \( g \) が単射、 \( f \) が全射であることが示せるので、 \( f,g \) は全単射となります。
このとき、逆写像の定義より次が成り立ちます。
$$ f^{-1}=g, \quad g^{-1}=f $$
数ベクトル空間
ここでは、今後よく用いられる数ベクトル空間について紹介します。
各成分が実数の \( n \) 次元ベクトル \( (a_1,a_2,\cdots,a_n) \) 全体の集合を \( n \) 次元数ベクトル空間もしくは \( n \) 次元実ベクトル空間といい、 \( \mathbb{R}^n \) と表す。
とくに、実数全体の集合は \( \mathbb{R} \) で表す。
また、各成分が複素数の \( n \) 次元ベクトル \( (a_1,a_2,\cdots,a_n) \) 全体の集合を \( n \) 次元複素ベクトル空間といい、 \( \mathbb{C}^n \) と表す。
とくに、複素数全体の集合は \( \mathbb{C} \) で表す。
(1) \( xy \) 平面の元 \( (x,y) \) は各成分が実数の \( 2 \) 次元ベクトルと考えることができるので、
$$ (x,y) \in \mathbb{R}^2 $$
(2) \( xyz \) 空間の元 \( (x,y,z) \) は各成分が実数の \( 3 \) 次元ベクトルと考えることができるので、
$$ (x,y,z) \in \mathbb{R}^3 $$
(3) 複素数 \( z \) は各成分が複素数の \( 1 \) 次元ベクトルと考えることができるので、
$$ z\in \mathbb{C} $$
となるが、複素数は \( z=x+iy \) により、2つの実数の組 \( (x,y) \) で表現することができる。
よって、複素数は \( 2 \) 次元数ベクトル空間 \( \mathbb{R}^2 \) の元であると見ることもできる。
(つまり、 \( \mathbb{C} \) は \( \mathbb{R}^2 \) であるとみなすことができる)
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

