こんにちは、ひかりです。
今回はベクトル解析からベクトルの内積・外積と3重積について解説していきます。
この記事では以下のことを紹介します。
- ベクトルの内積について
- ベクトルの外積について
- スカラー3重積とベクトル3重積について
ベクトルの内積
ここでは、ベクトルの内積について簡単に復習していきたいと思います。
詳しいことについては、線形代数学02や線形代数学続論12の記事をご覧ください。
まず、数ベクトルに対する内積について次の2つの定義がありました。
2つの \( n \) 次元ベクトル
$$ \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} $$
に対して、\( \mathbf{a} \) と \( \mathbf{b} \) の内積 \( \mathbf{a}\cdot\mathbf{b} \) を次で定義する。
$$ \mathbf{a}\cdot\mathbf{b}=a_1b_1+a_2b_2+\dots+a_nb_n. $$
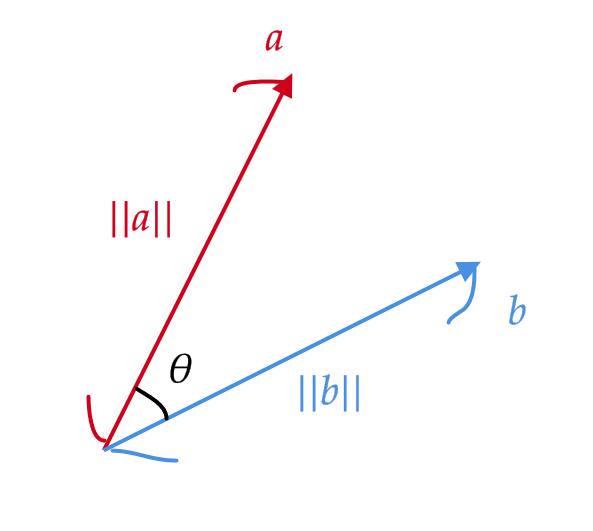
2つのベクトル \( \mathbf{a} \) と \( \mathbf{b} \) の長さ \( \|\mathbf{a}\|,\|\mathbf{b}\| \) とそのなす角 \( \theta \) に対して、 \( \mathbf{a} \) と \( \mathbf{b} \) の内積 \( \mathbf{a}\cdot\mathbf{b} \) を次で定義する。
$$ \mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta $$
(三角関数については、高校数学(数学Ⅲ)03の記事をご覧ください。)
これらは内積空間により一般化することができます。
まず、ベクトル空間の定義を述べておきましょう。(詳しくは線形代数学続論05をご覧ください)
集合 \( V \) に対して、和とスカラー倍の2つの演算が定義されているとする。つまり、
和: \( \mathbf{a},\mathbf{b}\in V \) に対して、 \( \mathbf{a}+\mathbf{b}\in V \) が定まる。
スカラー倍: \( \mathbf{a}\in V \) とスカラー \( k\in\mathbb{R} \) に対して、 \( k\mathbf{a}\in V \) が定まる。
このとき、任意の \( \mathbf{a},\mathbf{b},\mathbf{c}\in V \) とスカラー \( \lambda,\mu\in \mathbf{R} \) に対して、次の8つの性質をみたすとき、集合 \( V \) を \( \mathbb{R} \) 上のベクトル空間、もしくは実ベクトル空間という。
(1) \( \mathbf{a}+\mathbf{b}=\mathbf{b}+\mathbf{a} \)
(2) \( (\mathbf{a}+\mathbf{b})+\mathbf{c}=\mathbf{a}+(\mathbf{b}+\mathbf{c}) \)
(3) 任意の \( \mathbf{a}\in V \) に対して、 \( \mathbf{a}+\mathbf{0}=\mathbf{a} \) となる \( \mathbf{0}\in V \) が存在する。
(4) 任意の \( \mathbf{a}\in V \) に対して、 \( \mathbf{a}+\mathbf{a}’=\mathbf{0} \) となる \( \mathbf{a}’\in V \) が存在する。
(5) \( (\lambda\mu)\mathbf{a}=\lambda(\mu \mathbf{a}) \)
(6) \( (\lambda+\mu)\mathbf{a}=\lambda \mathbf{a}+\mu\mathbf{a} \)
(7) \( \lambda(\mathbf{a}+\mathbf{b})=\lambda\mathbf{a}+\mu\mathbf{a} \)
(8) \( 1\mathbf{a}=\mathbf{a} \)
また、スカラーを実数 \( \mathbb{R} \) からでなく、複素数 \( \mathbb{C} \) からとることもできる。
その場合は \( V \) を \( \mathbb{C} \) 上のベクトル空間、もしくは複素ベクトル空間という。
スカラーをとくに意識しないときは、単にベクトル空間とよぶことにして、スカラーの属する集合を \( K \) で表す。
つまり、 \( K=\mathbb{R} \ もしくは \ \mathbb{C} \) とする。
ベクトル空間に内積を導入したものが内積空間となります。
\( V \) を実ベクトル空間として、次の写像 \( (\cdot,\cdot):V\times V\to \mathbb{R} \) を考える。
$$ \mathbf{x},\mathbf{y}\mapsto (\mathbf{x},\mathbf{y}) $$
このとき、写像 \( (\cdot,\cdot) \) が次の4つの性質をみたすとき、 \( (\cdot,\cdot) \) を \( V \) の内積といい、 \( V=(V,(\cdot,\cdot)) \) のことを内積空間または計量ベクトル空間という。
ベクトル \( \mathbf{x},\mathbf{y},\mathbf{x}_1,\mathbf{x}_2\in V \) と \( \lambda\in \mathbb{R} \) に対して、
(1) \( (\mathbf{x},\mathbf{y})=(\mathbf{y},\mathbf{x}) \)
(2) \( (\mathbf{x}_1+\mathbf{x}_2,\mathbf{y})=(\mathbf{x}_1,\mathbf{y})+(\mathbf{x}_2,\mathbf{y}) \)
(3) \( (\lambda \mathbf{x},\mathbf{y})=\lambda(\mathbf{x}, \mathbf{y}) \)
(4) \( (\mathbf{x},\mathbf{x})≧0 \) さらに、\( (\mathbf{x},\mathbf{x})=0 \iff \mathbf{x}=\mathbf{0} \)
\( V \) を複素ベクトル空間として、次の写像 \( (\cdot,\cdot):V\times V\to \mathbb{C} \) を考える。
$$ \mathbf{x},\mathbf{y}\mapsto (\mathbf{x},\mathbf{y}) $$
このとき、写像 \( (\cdot,\cdot) \) が次の4つの性質をみたすとき、 \( (\cdot,\cdot) \) を \( V \) のエルミート内積もしくは内積といい、 \( V=(V,(\cdot,\cdot)) \) のことをエルミート内積空間または複素計量ベクトル空間という。
ベクトル \( \mathbf{x},\mathbf{y},\mathbf{x}_1,\mathbf{x}_2\in V \) と \( \lambda\in \mathbb{C} \) に対して、
(1) \( (\mathbf{x},\mathbf{y})=\overline{(\mathbf{y},\mathbf{x})} \)
(2) \( (\mathbf{x}_1+\mathbf{x}_2,\mathbf{y})=(\mathbf{x}_1,\mathbf{y})+(\mathbf{x}_2,\mathbf{y}) \)
(3) \( (\lambda \mathbf{x},\mathbf{y})=\lambda(\mathbf{x}, \mathbf{y}), \) \( (\mathbf{x},\lambda\mathbf{y})=\overline{\lambda}(\mathbf{x}, \mathbf{y}) \)
(4) \( (\mathbf{x},\mathbf{x})≧0 \) さらに、\( (\mathbf{x},\mathbf{x})=0 \iff \mathbf{x}=\mathbf{0} \)
ベクトル解析においては3次元の数ベクトルを考えることが多いので、3次元の標準基底
$$ \mathbf{e}_1=\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, \quad \mathbf{e}_2=\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, \quad \mathbf{e}_3=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} $$
を考えると、これらは正規直交基底であるので、
$$ \mathbf{e}_i\cdot \mathbf{e}_i=1, \quad \mathbf{e}_i\cdot \mathbf{e}_j=0, \ (i\not=j) $$
したがって、2つの3次元数ベクトル
$$ \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \quad \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} $$
をこの標準基底を用いて
$$ \mathbf{a}=a_1\mathbf{e}_1+a_2\mathbf{e}_2+a_3\mathbf{e}_3, \quad \mathbf{b}=b_1\mathbf{e}_1+b_2\mathbf{e}_2+b_3\mathbf{e}_3 $$
と表すと、 \( \mathbf{a},\mathbf{b} \) の内積は次のように計算できます。
$$ \begin{align} \mathbf{a}\cdot\mathbf{b}&=(a_1\mathbf{e}_1+a_2\mathbf{e}_2+a_3\mathbf{e}_3)\cdot(b_1\mathbf{e}_1+b_2\mathbf{e}_2+b_3\mathbf{e}_3) \\ &=(a_1b_1)\mathbf{e}_1\cdot\mathbf{e}_1+(a_2b_2)\mathbf{e}_2\cdot\mathbf{e}_2+(a_3b_3)\mathbf{e}_3\cdot\mathbf{e}_3 \quad (\mathbf{e}_i\cdot\mathbf{e}_j=0,i\not=j) \\ &=a_1b_1+a_2b_2+a_3b_3 \end{align} $$
\( \mathbf{a}=\begin{pmatrix} 6 \\ -3 \\ 2 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} 4 \\ 2 \\ -7 \end{pmatrix} \) のとき、 \( \mathbf{a}\cdot\mathbf{b} \) を求める。
$$ \mathbf{a}\cdot\mathbf{b}=6\times 4+(-3)\times 2+2\times (-7)=4 $$
ベクトルの外積
次にベクトルの外積について見ていきましょう。(詳しいことは線形代数学02の記事でも解説しています。)
まず、前提としてベクトルの外積は3次元ベクトルのみ定義することができます。
それ以外の次元では外積は考えることができないことに注意してください。
2つの \( 3 \) 次元ベクトル \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \) に対して、\( \mathbf{a} \) と \( \mathbf{b} \) の外積 \( \mathbf{a}\times\mathbf{b} \) を次で定義します。
$$ \mathbf{a}\times\mathbf{b}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}\times\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}=\begin{pmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{pmatrix}. $$
この定義は行列式を用いることにより、形式的に次のように表すことができます。
2つの3次元数ベクトル
$$ \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \quad \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} $$
をこの標準基底を用いて
$$ \mathbf{a}=a_1\mathbf{e}_1+a_2\mathbf{e}_2+a_3\mathbf{e}_3, \quad \mathbf{b}=b_1\mathbf{e}_1+b_2\mathbf{e}_2+b_3\mathbf{e}_3 $$
と表すと、
$$ \mathbf{a}\times\mathbf{b}=\begin{vmatrix} \mathbf{e}_1 & \mathbf{e}_2 & \mathbf{e}_3 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} $$
( \( \mathbf{e}_1,\mathbf{e}_2,\mathbf{e}_3 \) がベクトルより、本来この行列式は考えられないのであくまで形だけです)
実際、この行列式を計算してみると、
$$ \begin{align} \mathbf{a}\times\mathbf{b}&=a_2b_3\mathbf{e}_1+a_2b_1\mathbf{e}_2+a_1b_2\mathbf{e}_3 \\ & \quad -a_2b_2\mathbf{e}_1-a_1b_3\mathbf{e}_2-a_2b_1\mathbf{e}_2 \\ &=(a_2b_3-a_3b_2)\mathbf{e}_1+(a_3b_1-a_1b_3)\mathbf{e}_2+(a_1b_2-a_2b_1)\mathbf{e}_3 \\ &=\begin{pmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{pmatrix} \end{align} $$
となり、定義と一致します。
\( \mathbf{a}=\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} -1 \\ 1 \\ 3 \end{pmatrix} \) のとき、 \( \mathbf{a}\times\mathbf{b} \) を求める。
$$ \begin{align} \mathbf{a}\times\mathbf{b}&=\begin{vmatrix} \mathbf{e}_1 & \mathbf{e}_2 & \mathbf{e}_3 \\ 2 & 1 & 2 \\ -1 & 1 & 3 \end{vmatrix}=\mathbf{e}_1-8\mathbf{e}_2+3\mathbf{e}_3=\begin{pmatrix} 1 \\ -8 \\ 3 \end{pmatrix} \end{align} $$
スカラー3重積とベクトル3重積
スカラー3重積
ベクトルの内積は2つのベクトルからスカラーが得られ、ベクトルの外積は2つのベクトルからベクトルが得られます。
したがって、内積と外積を組み合わせることにより、3つのベクトルに対してベクトルの積を2つ考えることができます。
まず、1つ目にスカラー3重積を考えます。
3つの3次元ベクトル
$$ \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \quad \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}, \quad \mathbf{c}=\begin{pmatrix} c_1 \\ c_2 \\ c_3 \end{pmatrix} $$
に対して、スカラー3重積 \( (\mathbf{a},\mathbf{b},\mathbf{c}) \) を次で定義する。
$$ (\mathbf{a},\mathbf{b},\mathbf{c})=\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c}) $$
\( \mathbf{b}\times \mathbf{c} \) はベクトルであるので、スカラー3重積 \( (\mathbf{a},\mathbf{b},\mathbf{c}) \) はスカラーとなることに注意してください。
スカラー3重積は行列式を用いることにより、次のように表すことができます。
$$ (\mathbf{a},\mathbf{b},\mathbf{c})=\begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix} $$
実際、余因子展開を用いることにより、
$$ \begin{align} &(\mathbf{a},\mathbf{b},\mathbf{c}) \\ &=\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}\cdot \begin{vmatrix} \mathbf{e}_1 & \mathbf{e}_2 & \mathbf{e}_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix} \\ &=(a_1\mathbf{e}_1+a_2\mathbf{e}_2+a_3\mathbf{e}_3)\cdot \left( (-1)^{1+1}\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}\mathbf{e}_1+(-1)^{1+2}\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix} \mathbf{e}_2+(-1)^{1+3}\begin{vmatrix} b_1 & b_2 \\ c_1 & c_2 \end{vmatrix}\mathbf{e}_3 \right) \\ &=(-1)^{1+1}a_1\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}\mathbf{e}_1\cdot\mathbf{e}_1+(-1)^{1+2}a_2\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix} \mathbf{e}_2\cdot\mathbf{e}_2+(-1)^{1+3}a_3\begin{vmatrix} b_1 & b_2 \\ c_1 & c_2 \end{vmatrix}\mathbf{e}_3\cdot\mathbf{e}_3 \\ &=(-1)^{1+1}a_1\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}+(-1)^{1+2}a_2\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix}+(-1)^{1+3}a_3\begin{vmatrix} b_1 & b_2 \\ c_1 & c_2 \end{vmatrix} \\ &=\begin{vmatrix} a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix} \end{align} $$
$$ \mathbf{a}=\begin{pmatrix} 1 \\ -1 \\ 2 \end{pmatrix}, \quad \mathbf{b}=\begin{pmatrix} 2 \\ 0 \\ 1 \end{pmatrix}, \quad \mathbf{c}=\begin{pmatrix} -1 \\ 3 \\ 2 \end{pmatrix} $$
のとき、 \( (\mathbf{a},\mathbf{b},\mathbf{c}) \) を求める。
$$ \begin{align} (\mathbf{a},\mathbf{b},\mathbf{c})&=\mathbf{a}\cdot(\mathbf{b}\times \mathbf{c})=\begin{vmatrix} 1 & -1 & 2 \\ 2 & 0 & 1 \\ -1 & 3 & 2 \end{vmatrix}=14 \end{align} $$
また、スカラー3重積は行列式で表現することができるので、行列式の性質より次のことが成り立ちます。
3次元ベクトル \( \mathbf{a},\mathbf{b},\mathbf{c} \) のスカラー3重積について次が成り立つ。
(1) $$ \begin{align} (\mathbf{a},\mathbf{b},\mathbf{c})&=(\mathbf{b},\mathbf{c},\mathbf{a})=(\mathbf{c},\mathbf{a},\mathbf{b}) \\ &=-(\mathbf{a},\mathbf{c},\mathbf{b})=-(\mathbf{b},\mathbf{a},\mathbf{c})=-(\mathbf{c},\mathbf{b},\mathbf{a}) \end{align} $$
(2) $$ \begin{align} (\mathbf{0},\mathbf{b},\mathbf{c})&=(\mathbf{a},\mathbf{0},\mathbf{c})=(\mathbf{a},\mathbf{b},\mathbf{0})=0 \end{align} $$
(3) $$ \begin{align} (\mathbf{a},\mathbf{b},\mathbf{a})&=(\mathbf{a},\mathbf{a},\mathbf{b})=(\mathbf{b},\mathbf{a},\mathbf{a})=0 \end{align} $$
(4) スカラー3重積 \( (\mathbf{a},\mathbf{b},\mathbf{c}) \) の絶対値 \( |(\mathbf{a},\mathbf{b},\mathbf{c})| \) は \( \mathbf{a},\mathbf{b},\mathbf{c} \) を辺とする平行六面体の体積となる。
ベクトル3重積
次にベクトル3重積を考えます。
3つの3次元ベクトル
$$ \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix}, \quad \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}, \quad \mathbf{c}=\begin{pmatrix} c_1 \\ c_2 \\ c_3 \end{pmatrix} $$
に対して、
$$ \mathbf{a}\times (\mathbf{b}\times \mathbf{c}), \quad (\mathbf{a}\times\mathbf{b})\times \mathbf{c} $$
をベクトル3重積という。
\( \mathbf{b}\times \mathbf{c},\mathbf{a}\times\mathbf{b} \) はベクトルであるので、ベクトル3重積
$$ \mathbf{a}\times (\mathbf{b}\times \mathbf{c}), \quad (\mathbf{a}\times\mathbf{b})\times \mathbf{c} $$
はベクトルとなることに注意してください。
定義のまま計算するのは大変なので、まず次の性質を示します。
3次元ベクトル \( \mathbf{a},\mathbf{b},\mathbf{c} \) のベクトル3重積について次が成り立つ。
(1) $$ \begin{align} \mathbf{a}\times (\mathbf{b}\times \mathbf{c})&=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c} \end{align} $$
(2) $$ \begin{align} (\mathbf{a}\times\mathbf{b})\times \mathbf{c}&=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{b}\cdot\mathbf{c})\mathbf{a} \end{align} $$
定理2の証明(気になる方だけクリックしてください)
(1) 余因子展開より、
$$ \begin{align} \mathbf{b}\times \mathbf{c}&=\begin{vmatrix} \mathbf{e}_1 & \mathbf{e}_2 & \mathbf{e}_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3 \end{vmatrix} \\ &=(-1)^{1+1}\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}\mathbf{e}_1+(-1)^{1+2}\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix}\mathbf{e}_2+(-1)^{1+3}\begin{vmatrix} b_1 & b_2 \\ c_1& c_2 \end{vmatrix}\mathbf{e}_3 \\ &=\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}\mathbf{e}_1-\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix}\mathbf{e}_2+\begin{vmatrix} b_1 & b_2 \\ c_1& c_2 \end{vmatrix}\mathbf{e}_3 \end{align} $$
よって、外積の定義より、
$$ \begin{align} &\mathbf{a}\times (\mathbf{b}\times \mathbf{c}) \\ &=(a_1\mathbf{e}_1+a_2\mathbf{e}_2+a_3\mathbf{e}_3)\times \left( \begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}\mathbf{e}_1-\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix}\mathbf{e}_2+\begin{vmatrix} b_1 & b_2 \\ c_1& c_2 \end{vmatrix}\mathbf{e}_3 \right) \\ &=\left(a_2\begin{vmatrix} b_1 & b_2 \\ c_1& c_2 \end{vmatrix}+a_3\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix}\right)\mathbf{e}_1+\left( a_3\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}-a_1\begin{vmatrix} b_1 & b_2 \\ c_1& c_2 \end{vmatrix}\right)\mathbf{e}_2 \\ & \quad +\left( -a_3\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix}-a_2\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}\right)\mathbf{e}_3 \end{align} $$
まず、 \( \mathbf{e}_1 \) の項については、
$$ \begin{align} &a_2\begin{vmatrix} b_1 & b_2 \\ c_1& c_2 \end{vmatrix}+a_3\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix} \\ &=a_2(b_1c_2-b_2c_1)+a_2(b_1c_3-b_3c_1) \\ &=(a_2c_2+a_3c_3)b_1-(a_2b_2+a_3b_3)c_1 \\ &=(a_1c_1+a_2c_2+a_3c_3)b_1-(a_1b_1+a_2b_2+a_3b_3)c_1 \quad (a_1b_1c_1を足して引く) \\ &=(\mathbf{a}\cdot \mathbf{c})b_1-(\mathbf{a}\cdot\mathbf{b})c_1 \end{align} $$
同様にして、 \( \mathbf{e}_2,\mathbf{e}_3 \) の項は
$$ a_3\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}-a_1\begin{vmatrix} b_1 & b_2 \\ c_1& c_2 \end{vmatrix}=(\mathbf{a}\cdot \mathbf{c})b_2-(\mathbf{a}\cdot\mathbf{b})c_2 $$
$$ -a_3\begin{vmatrix} b_1 & b_3 \\ c_1 & c_3 \end{vmatrix}-a_2\begin{vmatrix} b_2 & b_3 \\ c_2 & c_3 \end{vmatrix}=(\mathbf{a}\cdot \mathbf{c})b_3-(\mathbf{a}\cdot\mathbf{b})c_3 $$
したがって、
$$ \begin{align} \mathbf{a}\times (\mathbf{b}\times \mathbf{c})&=\begin{pmatrix} (\mathbf{a}\cdot \mathbf{c})b_1-(\mathbf{a}\cdot\mathbf{b})c_1 \\ (\mathbf{a}\cdot \mathbf{c})b_2-(\mathbf{a}\cdot\mathbf{b})c_2 \\ (\mathbf{a}\cdot \mathbf{c})b_3-(\mathbf{a}\cdot\mathbf{b})c_3 \end{pmatrix} \\ &=(\mathbf{a}\cdot \mathbf{c})\begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix}-(\mathbf{a}\cdot\mathbf{b})\begin{pmatrix} c_1 \\ c_2 \\ c_3 \end{pmatrix} \\ &=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c} \end{align} $$
(2) 外積の性質と(1)より、
$$ \begin{align} (\mathbf{a}\times\mathbf{b})\times \mathbf{c}&=-\mathbf{c}\times(\mathbf{a}\times\mathbf{b}) \\ &=-\{ (\mathbf{c}\cdot\mathbf{b})\mathbf{a}-(\mathbf{c}\cdot\mathbf{a})\mathbf{b}\} \\ &=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{b}\cdot\mathbf{c})\mathbf{a} \end{align} $$
$$ \mathbf{a}=\begin{pmatrix} 2 \\ 1 \\ 3 \end{pmatrix}, \quad \mathbf{b}=\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}, \quad \mathbf{c}=\begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix} $$
のとき、 \( \mathbf{a}\times (\mathbf{b}\times \mathbf{c}) \) を求める。
$$ \begin{align} \mathbf{a}\times (\mathbf{b}\times \mathbf{c})&=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c}=9\mathbf{b}-\mathbf{c}=\begin{pmatrix} -10 \\ -1 \\ 7 \end{pmatrix} \end{align} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

