こんにちは、ひかりです。
今回は確率・統計から正規性の検討と母相関係数の仮説検定について解説していきます。
この記事では以下のことを紹介します。
- 正規Q-Qプロットによる正規性の検討について
- 歪度と尖度による正規性の検討について
- 母相関係数と無相関性の仮説検定について
正規Q-Qプロットによる正規性の検討
いままでの記事において様々な仮説検定について紹介してきました。
そのとき、いくつかの仮説検定では正規母集団という仮定が必要でした。
では、どのようにして母集団が正規分布に従っていると調べるのでしょうか。
その方法はいくつかありますが、ここでは2つ紹介していきます。
まずは、正規Q-Qプロットを用いる方法について解説しています。
2つの確率変数 \( X,Y \) の従う確率分布を比較するために用いられるグラフのことをQ-Qプロットといいます。
特に、確率変数 \( X \) の分布を正規分布として、確率変数 \( Y \) が正規分布にどれだけ近いのかを見るときに用いられるQ-Qプロットを正規Q-Qプロットといいます。
正規Q-Qプロットの作り方と正規性の調べ方の流れは以下のようになります。
(抽出した標本などの)実現値を \( y_1,\cdots,y_n \) とします。
ただし、実現値は小さい順にならべておきます。
まず、任意の実数 \( y \) に対して、 \( y \) 以下となるような実現値の個数を \( \# \{ y_i≦y \} \) とおきます。
このとき、 \( y_1,\cdots,y_n \) の経験分布関数 \( F_n(y) \) を次で定義します。
$$ F_n(y)=\frac{\# \{ y_i≦y \}}{n} $$
(\( 0≦\# \{ y_i≦y \}≦n \) より、 \( 0≦F_n(y)≦1 \) であることに注意してください)
標準正規分布の分布関数を \( F_x(x) \) とおきます。
このとき、各実現値 \( y_1,\cdots,y_n \) に対して、
$$ F_x(x_i)=F_n(y_i) $$
となる点の組 \( (x_i,y_i) \) を求めます。
この点の組 \( (x_i,y_i) \) のことを \( 100p \) %分位点といいます。
ここで、 \( p \) は
$$ F_x(x_i)=F_n(y_i)=p $$
となる \( p \) のことです。
STEP2で求めた点の組 \( (x_i,y_i) \) を横軸が \( x_i \) 、縦軸が \( y_i \) となるように、プロットしていきます。
そのグラフのことを正規Q-Qプロットといいます。
STEP3で作成した正規Q-Qプロットの各点が何かしらの直線で近似することができるのかを見ます。
(具体的には今後解説する回帰分析などを用います)
ここで、もし正規Q-Qプロットの各点が
$$ y=\mu+\sigma x $$
という直線で近似できた場合には母集団は正規分布 \( N(\mu,\sigma^2) \) に近似的に従うことが知られています。
(詳細は省略します。)
ある工場の製品20個の重量(g)を測ったところ次のようであった。
$$ 149, \ 154, \ 160, \ 160, \ 165, \ 156, \ 158, \ 156, \ 152, \ 160 $$
$$ 154, \ 162, \ 156, \ 162, \ 157, \ 162, \ 162, \ 161, \ 153, \ 164 $$
このとき、正規Q-Qプロットを作成すると次のようになる。
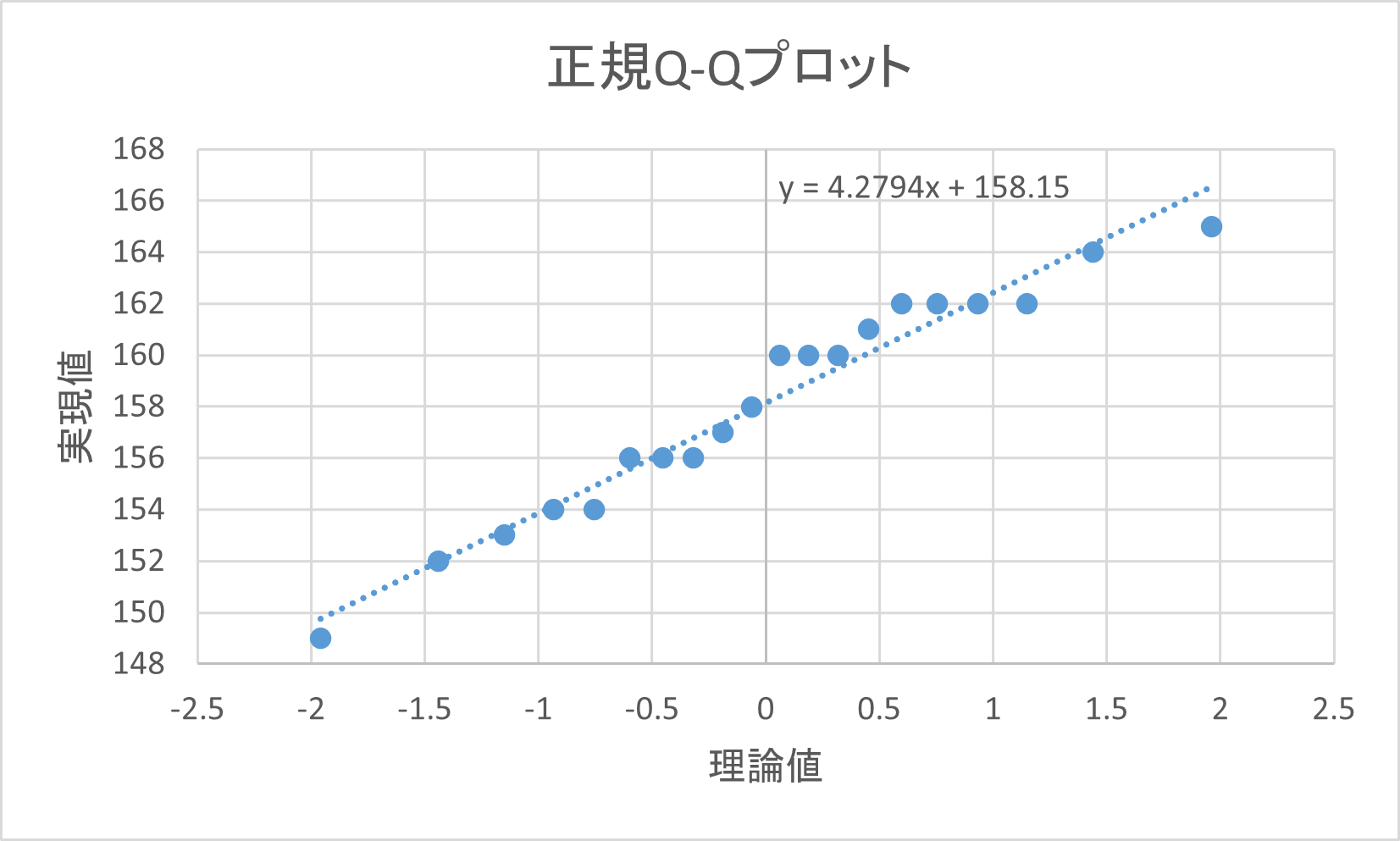
これは直線
$$ y=4.2794x+158.15 $$
で近似することができるので、この製品の重量は正規分布 \( N(158.15,4.28^2) \) に近似的に従っていると考えられる。
歪度と尖度による正規性の検討
もう一つの正規性の検討の方法としては、歪度と尖度を調べる方法があります。
確率・統計08の記事にて、歪度と尖度を次のように定義しました。
確率変数 \( X \) に対して、平均を \( \mu \) 、標準偏差を \( \sigma \) とおく。
このとき、 \( X \) の確率分布の歪度 \( \alpha_3 \) を次で定める。
$$ \alpha_3=\frac{E[(X-\mu)^3]}{\sigma^3} $$
確率変数 \( X \) に対して、平均を \( \mu \) 、標準偏差を \( \sigma \) とおく。
このとき、 \( X \) の確率分布の尖度 \( \alpha_4 \) を次で定める。
$$ \alpha_4=\frac{E[(X-\mu)^4]}{\sigma^4} $$
ただし、 \( \alpha_4-3 \) を確率分布の尖度ということもある。
まず、正規分布の歪度は \( \alpha_3=0 \) 、尖度は \( \alpha_4=3 \) (つまり \( \alpha_4-3=0 \) )であることに注意します。
そして、これをもとにして、母集団から抽出した標本 \( X_1,\cdots,X_n \) に対する標本歪度と標本尖度を次のように定義します。
母集団から抽出した標本 \( X_1,\cdots,X_n \) に対して、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad s^2=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^2 $$
$$ m_3=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^3 $$
とおく。このとき、 \( X_1,\cdots,X_n \) の標本歪度 \( \gamma_3 \) を次で定める。
$$ \gamma_3=\frac{m_3}{s^3} $$
母集団から抽出した標本 \( X_1,\cdots,X_n \) に対して、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad s^2=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^2 $$
$$ m_4=\frac{1}{n}\sum_{i=1}^n(X_i-\overline{X})^4 $$
とおく。このとき、 \( X_1,\cdots,X_n \) の標本尖度 \( \gamma_4 \) を次で定める。
$$ \gamma_4=\frac{m_4}{s^4} $$
ただし、 \( \gamma_4-3 \) を標本尖度ということもある。
母集団から抽出した標本に対して、標本歪度と標本尖度を求めて、それらがそれぞれ \( 0 \) と \( 3 \) に近いかどうかを調べることにより、母集団が正規分布に従っているかがわかります。
母相関係数と無相関性の仮説検定
2次元正規母集団の母相関係数の仮説検定
最後に、2次元正規分布 \( N(\mu_1,\mu_2,\sigma^2_1,\sigma^2_2,\rho) \) に従う母集団から抽出した標本 \( (X_1,Y_1),\cdots,(X_n,Y_n) \) に対して、母相関係数 \( \rho \) に関する仮説検定について考えてみましょう。
ただし、母数 \( \mu_1,\mu_2,\sigma^2_1,\sigma^2_2 \) はすべて未知であるとして、標本数 \( n \) は十分大きいものとします。
まず、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S_1^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
$$ \overline{Y}=\frac{1}{n}\sum_{i=1}^nY_i, \quad S_2^2=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\overline{Y})^2 $$
とするとき、標本相関係数 \( r \) を次で定めます。
$$ \begin{align} r&=\frac{\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{S_1^2S_2^2}} \\ &=\frac{\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{(n-1)S_1S_2} \end{align} $$
このとき、
$$ Z=\frac{1}{2}\log \frac{1+r}{1-r} $$
とおくと、 \( n \) が十分大きいとき(目安は \( n≧100 \))、近似的に正規分布 \( N\left(\frac{1}{2}\log \frac{1+\rho}{1-\rho},\frac{1}{n-3} \right) \) に従うことが知られています。
(詳細は省略します。)
この変換のことをフィッシャーのz変換といいます。
したがって、検定統計量 \( T \) を \( Z \) の標準化
$$ T=\sqrt{n-3}\left( \frac{1}{2}\log \frac{1+r}{1-r}-\frac{1}{2}\log \frac{1+\rho}{1-\rho} \right) $$
は近似的に標準正規分布 \( N(0,1) \) に従います。
よって、両側検定
$$ H_0:\rho=\rho_0, \quad H_1:\rho\not=\rho_0 $$
を考えると、検定統計量 \( T \) は
$$ T=\sqrt{n-3}\left( \frac{1}{2}\log \frac{1+r}{1-r}-\frac{1}{2}\log \frac{1+\rho_0}{1-\rho_0} \right) $$
となり、有意水準 \( 0.05 \) の両側検定の棄却域 \( R \) は
$$ \begin{align} 0.05&=1-0.95=1-P\left( -1.96≦T≦1.96 \right) \\ &=P(\{ T<-1.96\}\cup\{ T>1.96\}) \end{align} $$
より、
$$ R=\{ T<-1.96\}\cup\{ T>1.96\} $$
となります。同様に有意水準 \( 0.01 \) の両側検定の棄却域 \( R \) は
$$ R=\{ T<-2.58\}\cup\{ T>2.58\} $$
まとめると、
母集団が2次元正規分布 \( N(\mu_1,\mu_2,\sigma^2_1,\sigma^2_2,\rho) \) に従っていて、母数 \( \mu_1,\mu_2,\sigma^2_1,\sigma^2_2 \) はすべて未知であるとする。
また、標本数 \( n \) は十分大きい(目安は \( n≧100 \))とする。
ここで、2次元正規母集団から抽出した標本を \( (X_1,Y_1),\cdots,(X_n,Y_n) \) として、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S_1^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
$$ \overline{Y}=\frac{1}{n}\sum_{i=1}^nY_i, \quad S_2^2=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\overline{Y})^2 $$
$$ \begin{align} r&=\frac{\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{S_1^2S_2^2}} \\ &=\frac{\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{(n-1)S_1S_2} \end{align} $$
とおく。
このとき、仮説 \( H_0:\rho=\rho_0, \quad H_1:\rho\not=\rho_0 \) に対して、有意水準 \( 0.05,0.01 \) の母相関係数 \( \rho \) の両側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\sqrt{n-3}\left( \frac{1}{2}\log \frac{1+r}{1-r}-\frac{1}{2}\log \frac{1+\rho_0}{1-\rho_0} \right) $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-1.96\}\cup\{ T>1.96\} $$
$$ 有意水準0.01 \quad R=\{ T<-2.58\}\cup\{ T>2.58\} $$
同様に片側検定の場合は次のようになります。
母集団が2次元正規分布 \( N(\mu_1,\mu_2,\sigma^2_1,\sigma^2_2,\rho) \) に従っていて、母数 \( \mu_1,\mu_2,\sigma^2_1,\sigma^2_2 \) はすべて未知であるとする。
また、標本数 \( n \) は十分大きい(目安は \( n≧100 \))とする。
ここで、2次元正規母集団から抽出した標本を \( (X_1,Y_1),\cdots,(X_n,Y_n) \) として、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S_1^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
$$ \overline{Y}=\frac{1}{n}\sum_{i=1}^nY_i, \quad S_2^2=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\overline{Y})^2 $$
$$ \begin{align} r&=\frac{\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{S_1^2S_2^2}} \\ &=\frac{\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{(n-1)S_1S_2} \end{align} $$
とおく。
このとき、仮説 \( H_0:\rho=\rho_0, \quad H_1:\rho<(>)\rho_0 \) に対して、有意水準 \( 0.05,0.01 \) の母相関係数 \( \rho \) の片側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\sqrt{n-3}\left( \frac{1}{2}\log \frac{1+r}{1-r}-\frac{1}{2}\log \frac{1+\rho_0}{1-\rho_0} \right) $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-1.645\} \ (\{T>1.645\}) $$
$$ 有意水準0.01 \quad R=\{ T<-2.33 \}\ (\{ T>2.33\}) $$
ある学校の高校1年生の国語と英語のテストの間には \( \rho=0.3 \) の相関があることが知られている。
ここで、この学校の高校1年生から100人を選んで国語と英語のテストの点数を調べたところ、その相関係数は \( r=0.21 \) であった。
このとき、 \( \rho=0.3 \) は正しいといえるかを有意水準 \( 0.05 \) で検定する。
まず、帰無仮説を \( H_0:\rho=0.3 \) とおき、対立仮説を \( H_1:\rho\not=0.3 \) とおく。
また、有意水準は \( 0.05 \) である。
帰無仮説 \( H_0 \) が正しいとすると、検定統計量
$$ T=\sqrt{97}\left( \frac{1}{2}\log \frac{1+r}{1-r}-\frac{1}{2}\log \frac{1.3}{0.7} \right) $$
は標準正規分布 \( N(0,1) \) に従う。
このとき、定理1より有意水準 \( 0.05 \) の棄却域 \( R \) は
$$ \begin{align} R&=\{ T<-1.96\}\cup\{ T>1.96\} \end{align} $$
となる。したがって、
$$ r=0.21 $$
より、検定統計量 \( T \) の実現値 \( T^* \) が
$$ T^*=\sqrt{97}\left( \frac{1}{2}\log \frac{1+0.21}{1-0.21}-\frac{1}{2}\log \frac{1.3}{0.7} \right)≒0.949\not\in R $$
となるので、帰無仮説 \( H_0 \) は受容される。
よって、 \( \rho=0.3 \) は正しくないとはいいきれない。
( \( \rho=0.3 \) は正しいとまではいえないことに注意)
2次元正規母集団の無相関性の仮説検定
母相関係数の仮説検定の中でも、無相関性(つまり、 \( \rho=0 \))の仮説検定は標本数が少ない場合においても行うことができます。
(つまり、フィッシャーのz変換を用いない方法で検定することができます)
まず、2次元正規分布 \( N(\mu_1,\mu_2,\sigma^2_1,\sigma^2_2,\rho) \) に従う母集団から抽出した標本 \( (X_1,Y_1),\cdots,(X_n,Y_n) \) に対して、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S_1^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
$$ \overline{Y}=\frac{1}{n}\sum_{i=1}^nY_i, \quad S_2^2=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\overline{Y})^2 $$
$$ \begin{align} r&=\frac{\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{S_1^2S_2^2}} \\ &=\frac{\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{(n-1)S_1S_2} \end{align} $$
とおきます。
このとき、両側検定
$$ H_0:\rho=0, \quad H_1:\rho\not=0 $$
を考えて、次のように検定統計量 \( T \) を定めます。
$$ T=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}} $$
このとき、仮定 \( \rho=0 \) のもと \( T \) は自由度 \( n-2 \) の \( t \) 分布 \( t(n-2) \) に従うことが知られています。
(詳細は省略します。)
したがって、有意水準 \( 0.05 \) の両側検定の棄却域 \( R \) は
$$ \begin{align} 0.05&=1-0.95=1-P\left( -t_{0.025}(n-2)≦T≦t_{0.025}(n-2) \right) \\ &=P(\{ T<-t_{0.025}(n-2)\}\cup\{ T>t_{0.025}(n-2)\}) \end{align} $$
より、
$$ R=\{ T<-t_{0.025}(n-2)\}\cup\{ T>t_{0.025}(n-2)\} $$
となります。同様に有意水準 \( 0.01 \) の両側検定の棄却域 \( R \) は
$$ R=\{ T<-t_{0.005}(n-2)\}\cup\{ T>t_{0.005}(n-2)\} $$
まとめると、
母集団が2次元正規分布 \( N(\mu_1,\mu_2,\sigma^2_1,\sigma^2_2,\rho) \) に従っていて、母数 \( \mu_1,\mu_2,\sigma^2_1,\sigma^2_2 \) はすべて未知であるとする。
ここで、2次元正規母集団から抽出した標本を \( (X_1,Y_1),\cdots,(X_n,Y_n) \) として、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S_1^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
$$ \overline{Y}=\frac{1}{n}\sum_{i=1}^nY_i, \quad S_2^2=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\overline{Y})^2 $$
$$ \begin{align} r&=\frac{\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{S_1^2S_2^2}} \\ &=\frac{\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{(n-1)S_1S_2} \end{align} $$
とおく。
このとき、仮説 \( H_0:\rho=0, \quad H_1:\rho\not=0 \) に対して、有意水準 \( 0.05,0.01 \) の母相関係数 \( \rho \) の両側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}} $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-t_{0.025}(n-2)\}\cup\{ T>t_{0.025}(n-2)\} $$
$$ 有意水準0.01 \quad R=\{ T<-t_{0.005}(n-2)\}\cup\{ T>t_{0.005}(n-2)\} $$
同様に片側検定の場合は次のようになります。
母集団が2次元正規分布 \( N(\mu_1,\mu_2,\sigma^2_1,\sigma^2_2,\rho) \) に従っていて、母数 \( \mu_1,\mu_2,\sigma^2_1,\sigma^2_2 \) はすべて未知であるとする。
ここで、2次元正規母集団から抽出した標本を \( (X_1,Y_1),\cdots,(X_n,Y_n) \) として、
$$ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i, \quad S_1^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
$$ \overline{Y}=\frac{1}{n}\sum_{i=1}^nY_i, \quad S_2^2=\frac{1}{n-1}\sum_{i=1}^n(Y_i-\overline{Y})^2 $$
$$ \begin{align} r&=\frac{\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{S_1^2S_2^2}} \\ &=\frac{\sum_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{(n-1)S_1S_2} \end{align} $$
とおく。
このとき、仮説 \( H_0:\rho=0, \quad H_1:\rho<(>)0 \) に対して、有意水準 \( 0.05,0.01 \) の母相関係数 \( \rho \) の片側検定の棄却域 \( R \) は次のようになる。
検定統計量を
$$ T=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}} $$
とするとき、
$$ 有意水準0.05 \quad R=\{ T<-t_{0.05}(n-2)\} \ (\{T>t_{0.05}(n-2)\}) $$
$$ 有意水準0.01 \quad R=\{ T<-t_{0.01}(n-2) \}\ (\{ T>t_{0.01}(n-2)\}) $$
ある学校の高校3年生から20人を選んで国語と数学のテストの点数を調べたところ、その相関係数は \( r=0.5 \) であった。
このとき、この学校の高校3年生の国語と数学のテストの点数は無相関であるといえるかを有意水準 \( 0.05 \) で検定する。
まず、帰無仮説を \( H_0:\rho=0 \) とおき、対立仮説を \( H_1:\rho\not=0 \) とおく。
また、有意水準は \( 0.05 \) である。
帰無仮説 \( H_0 \) が正しいとすると、検定統計量
$$ T=\frac{r\sqrt{18}}{\sqrt{1-r^2}} $$
は自由度 \( 18 \) の \( t \) 分布 \( t(18) \) に従う。
このとき、定理3より有意水準 \( 0.05 \) の棄却域 \( R \) は
$$ \begin{align} R&=\{ T<-t_{0.025}(18)\}\cup\{ T>t_{0.025}(18)\} \\ &=\{ T<-2.101\}\cup\{ T>2.101\} \end{align} $$
となる。したがって、
$$ r=0.5 $$
より、検定統計量 \( T \) の実現値 \( T^* \) が
$$ T^*=\frac{0.5\times\sqrt{18}}{\sqrt{1-0.5^2}}≒2.449\in R $$
となるので、帰無仮説 \( H_0 \) は棄却される。
よって、この学校の高校3年生の国語と数学のテストの点数は無相関であるとはいえない。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

