こんにちは、ひかりです。
今回は確率・統計からカイ2乗分布・t分布・F分布について解説していきます。
この記事では以下のことを紹介します。
- カイ2乗分布について
- t分布について
- F分布について
カイ2乗分布
確率・統計15の記事において、母集団から抽出した互いに独立な標本 \( X_1,\cdots,X_n \) における
$$ 標本平均 \ \overline{X}=\frac{1}{n}\sum_{i=1}^nX_i $$
$$ 標本分散 \ S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline{X})^2 $$
を紹介しました。
今回はその標本平均や標本分散などが従う確率分布(標本分布とよびました)について見ていきましょう。
確率変数 \( X_1,\cdots,X_n \) が互いに独立で標準正規分布 \( N(0,1) \) に従うとします。このとき、
$$ X^2=X_1^2+\cdots+X_n^2 $$
が従う確率分布を自由度 \( n \) のカイ2乗分布といい、 \( \chi^2(n) \) と表します。
とくに、確率変数 \( X \) が標準正規分布 \( N(0,1) \) に従うとき、 \( X^2 \) が自由度 \( 1 \) のカイ2乗分布 \( \chi^2(1) \) に従います。
確率変数 \( X \) が自由度 \( n \) のカイ2乗分布 \( \chi^2(n) \) に従うとき、確率密度関数 \( f_X(x) \) は次のようになります。(複雑なので覚える必要はないです。上の定義でおさえておきましょう)
$$ f_X(x)=\begin{cases} \frac{1}{2^{\frac{n}{2}}\Gamma\left(\frac{n}{2}\right)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}} & (x>0) \\ 0 & (x≦0) \end{cases} $$
ここで、 \( \Gamma(s) \) はガンマ関数であり、
$$ \Gamma(s)=\int_0^{\infty}x^{s-1}e^{-x}dx \quad (s>0) $$
で定義されます。(詳しい性質については微分積分学06をご覧ください。)
確率密度関数 \( f_X(x) \) のグラフを自由度 \( n \) ごとに表すと次のようになります。
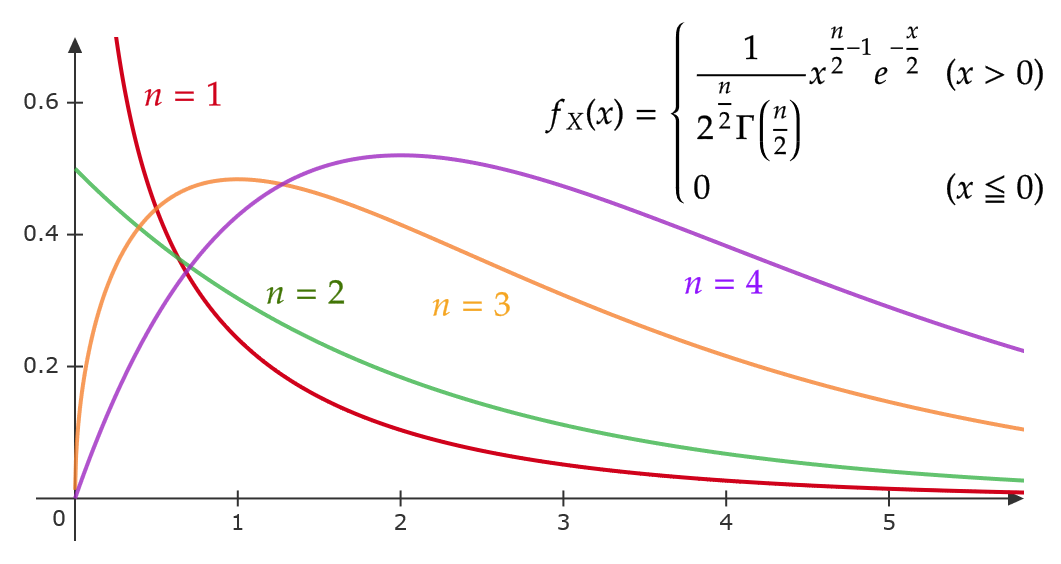
なぜ、この分布がカイ2乗分布とよばれているのかというと、ギリシャ語で \( X \) に対応する文字が \( \chi \) (カイと読みます)であり、 \( X^2 \) が従う確率分布であるためです。
自由度 \( n \) のカイ2乗分布 \( \chi^2(n) \) に従う確率変数 \( X \) の上側確率
$$ P(X≧x)=\alpha $$
となる \( x \) の値はカイ2乗分布表という表にまとめられています。
(カイ2乗分布表は確率・統計の参考書や問題集をご覧ください。このサイトでは東京大学出版会の統計学入門や統計検定2級の公式参考書の表を参考に計算しています。)
確率変数 \( X \) が自由度 \( 17 \) のカイ2乗分布 \( \chi^2(17) \) に従っているとする。
このとき、次の2つの確率を求める。
$$ \begin{align} &P(X≦8.67) \\ &=1-P(X≧8.67) \\ &=1-0.95 \\ & (自由度17でカイ2乗分布表を横にみて、8.67に一番近い\alphaをみつける) \\ &=0.05 \end{align} $$
$$ \begin{align} &P(12.79≦X≦27.6) \\ &=P(X≦27.6)-P(X≦12.79) \\ &=\{ 1-P(X≧27.6) \}-\{ 1-P(X≧12.79)\} \\ &=\{ 1-0.05\}-\{1-0.75\} \\ & (自由度17でカイ2乗分布表を横にみて、12.79,27.6に一番近い\alphaをみつける) \\ &=0.7 \end{align} $$
カイ2乗分布の性質として、次が成り立ちます。
確率変数 \( X \) が自由度 \( n \) のカイ2乗分布 \( \chi^2(n) \) に従っているとする。このとき、
(1) $$ \int_{-\infty}^{\infty}f_X(x)dx=\int_0^{\infty}\frac{1}{2^{\frac{n}{2}}\Gamma\left(\frac{n}{2}\right)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}dx=1 $$
(2) $$ E(X)=n, \quad V(X)=2n $$
(3) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=(1-2t)^{-\frac{n}{2}}, \quad \left(t<\frac{1}{2}\right) $$
(4) (カイ2乗分布の再生性) 確率変数 \( Y \) が自由度 \( m \) のカイ2乗分布 \( \chi^2(m) \) に従っているとする。
また、 \( X \) と \( Y \) が独立であるとする。
このとき、 \( X+Y \) は自由度 \( n+m \) のカイ2乗分布 \( \chi^2(n+m) \) に従う。
定理1の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} \int_{-\infty}^{\infty}f_X(x)dx&=\int_0^{\infty}\frac{1}{2^{\frac{n}{2}}\Gamma\left(\frac{n}{2}\right)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}dx \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\frac{1}{2}\left(\frac{x}{2}\right)^{\frac{n}{2}-1}e^{-\frac{x}{2}}dx \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}y^{\frac{n}{2}-1}e^{-y}dy \quad \left(y=\frac{x}{2}, \ \frac{1}{2}dx=dy\right) \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\Gamma\left(\frac{n}{2}\right)=1 \end{align} $$
(2) 微分積分学06の定理8(1)より、
$$ \begin{align} E(X)&=\int_0^{\infty}\frac{x}{2^{\frac{n}{2}}\Gamma\left(\frac{n}{2}\right)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}dx \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\left(\frac{x}{2}\right)^{\frac{n+2}{2}-1}e^{-\frac{x}{2}}dx \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}2y^{\frac{n+2}{2}-1}e^{-y}dy \quad \left(y=\frac{x}{2}, \ \frac{1}{2}dx=dy\right) \\ &=\frac{2}{\Gamma\left(\frac{n}{2}\right)}\Gamma\left(\frac{n+2}{2}\right) \\&=\frac{2}{\Gamma\left(\frac{n}{2}\right)}\cdot\frac{n}{2}\Gamma\left( \frac{n}{2} \right) \quad (微分積分学06の定理8(1)) \\ &=n \end{align} $$
また、
$$ \begin{align} E(X^2)&=\int_0^{\infty}\frac{x^2}{2^{\frac{n}{2}}\Gamma\left(\frac{n}{2}\right)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}dx \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}2\left(\frac{x}{2}\right)^{\frac{n+4}{2}-1}e^{-\frac{x}{2}}dx \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}4y^{\frac{n+4}{2}-1}e^{-y}dy \quad \left(y=\frac{x}{2}, \ \frac{1}{2}dx=dy\right) \\ &=\frac{4}{\Gamma\left(\frac{n}{2}\right)}\Gamma\left(\frac{n+4}{2}\right) \\&=\frac{4}{\Gamma\left(\frac{n}{2}\right)}\cdot\frac{n+2}{2}\cdot\frac{n}{2}\Gamma\left( \frac{n}{2} \right) \quad (微分積分学06の定理8(1)) \\ &=n(n+2) \end{align} $$
より、
$$ \begin{align} V(X)&=E(X^2)-\{ E(X)\}^2=n(n+2)-n^2=2n \end{align} $$
(3) \( t<\frac{1}{2} \) のとき、
$$ \begin{align} M_X(t)&=E(e^{tX})=\int_0^{\infty}\frac{e^{tx}}{2^{\frac{n}{2}}\Gamma\left(\frac{n}{2}\right)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}dx \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\frac{1}{2^{\frac{n}{2}}}x^{\frac{n}{2}-1}e^{-x\left(\frac{1}{2}-t\right)}dx \\ &=\frac{1}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\frac{1}{2^{\frac{n}{2}}}y^{\frac{n}{2}-1}(1-2t)^{-\frac{n}{2}}e^{-\frac{y}{2}}dy \quad \left(y=(1-2t)x, \ (1-2t)dx=dy\right) \\ &=\frac{(1-2t)^{-\frac{n}{2}}}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\frac{1}{2}\left(\frac{y}{2}\right)^{\frac{n}{2}-1}e^{-\frac{y}{2}}dy \\ &=\frac{(1-2t)^{-\frac{n}{2}}}{\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}z^{\frac{n}{2}-1}e^{-z}dz \quad \left(y=\frac{x}{2}, \ \frac{1}{2}dx=dy\right) \\&=\frac{(1-2t)^{-\frac{n}{2}}}{\Gamma\left(\frac{n}{2}\right)}\Gamma\left(\frac{n}{2}\right)=(1-2t)^{-\frac{n}{2}} \end{align} $$
(\( t≧\frac{1}{2} \) のときは積分が発散してしまいます)
(4) \( X \) のモーメント母関数は \( (1-2t)^{-\frac{n}{2}} \) 、 \( Y \) のモーメント母関数は \( (1-2t)^{-\frac{m}{2}} \) である。
このとき、 \( X+Y \) のモーメント母関数は \( X \) と \( Y \) は独立であるので、確率・統計09の定理3のあとの注意より、
$$ \begin{align} M_{X+Y}(t)&=E(e^{X+Y})=E(e^Xe^Y) \\ &=E(e^X)E(e^Y) \quad (XとYは独立であることより) \\ &=(1-2t)^{-\frac{n}{2}}(1-2t)^{-\frac{m}{2}}=(1-2t)^{-\frac{n+m}{2}} \end{align} $$
したがって、 \( X+Y \) は \( \chi^2(n+m) \) に従う。
標本分布とカイ2乗分布との関係について、次が成り立ちます。
\( X_1,\cdots,X_n \) は互いに独立で正規分布 \( N(\mu,\sigma^2) \) に従うとする。
(つまり、 \( X_i \) は正規母集団 \( N(\mu,\sigma^2) \) からの標本であると考えられる)
また、 \( X_1,\cdots,X_n \) の標本平均を \( \overline{X} \) 、標本分散を \( S^2 \) とする。
このとき、次の2つが成り立つ。
(1) $$ \sum_{i=1}^n\left( \frac{X_i-\mu}{\sigma} \right)^2 $$
は自由度 \( n \) のカイ2乗分布 \( \chi^2(n) \) に従う。
(2) $$ \sum_{i=1}^n\left( \frac{X_i-\overline{X}}{\sigma} \right)^2=\frac{(n-1)S^2}{\sigma^2} $$
は自由度 \( n-1 \) のカイ2乗分布 \( \chi^2(n-1) \) に従う。
定理2の証明(気になる方だけクリックしてください)
(1) 各 \( X_i \) は正規分布 \( N(\mu,\sigma^2) \) に従うので、標準化 \( \frac{X_i-\mu}{\sigma} \) は標準正規分布 \( N(0,1) \) に従います。
また、 \( X_1,\cdots,X_n \) は互いに独立であるので、
$$ \frac{X_1-\mu}{\sigma}, \cdots,\frac{X_n-\mu}{\sigma} $$
も互いに独立となります。
よって、カイ2乗分布の定義より、
$$ \sum_{i=1}^n\left( \frac{X_i-\mu}{\sigma} \right)^2 $$
は自由度 \( n \) のカイ2乗分布 \( \chi^2(n) \) に従います。
(2) $$ \begin{align} &\sum_{i=1}^n\left( \frac{X_i-\mu}{\sigma} \right)^2 \\ &=\frac{1}{\sigma^2}\sum_{i=1}^n(X_i-\overline{X}+\overline{X}-\mu)^2 \\ &=\frac{1}{\sigma^2}\sum_{i=1}^n(X_i-\overline{X})^2+\frac{2}{\sigma^2}(\overline{X}-\mu)\sum_{i=1}^n(X_i-\overline{X})+\frac{1}{\sigma^2}\sum_{i=1}^n(\overline{X}-\mu)^2 \\ &=\frac{1}{\sigma^2}\sum_{i=1}^n(X_i-\overline{X})^2+\frac{n}{\sigma^2}(\overline{X}-\mu)^2 \quad (上の第2項は0となる) \\ &=\sum_{i=1}^n\left( \frac{X_i-\overline{X}}{\sigma} \right)^2+\left( \frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \right)^2 \end{align} $$
したがって、
$$ \sum_{i=1}^n\left( \frac{X_i-\overline{X}}{\sigma} \right)^2=\sum_{i=1}^n\left( \frac{X_i-\mu}{\sigma} \right)^2-\left( \frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \right)^2 $$
左辺の第1項は(1)より \( \chi^2(n) \) に、第2項は \( \frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}} \) が標準正規分布 \( N(0,1) \) に従うので \( \chi^2(1) \) に従います。
また、この2つの確率変数は独立であることが示せます。(詳しくは省略します)
したがって、カイ2乗分布の再生性より、
$$ \sum_{i=1}^n\left( \frac{X_i-\overline{X}}{\sigma} \right)^2=\frac{(n-1)S^2}{\sigma^2} $$
は自由度 \( n-1 \) のカイ2乗分布 \( \chi^2(n-1) \) に従います。
t分布
確率変数 \( X,Y \) が互いに独立で \( X \) が標準正規分布 \( N(0,1) \) 、 \( Y \) が自由度 \( n \) のカイ2乗分布 \( \chi^2(n) \) に従うとします。このとき、
$$ T=\frac{X}{\sqrt{\frac{Y}{n}}} $$
が従う確率分布を自由度 \( n \) の \( t \) 分布もしくは自由度 \( n \) のスチューデントの \( t \) 分布といい、 \( t(n) \) と表します。
確率変数 \( X \) が自由度 \( n \) の \( t \) 分布 \( t(n) \) に従うとき、確率密度関数 \( f_X(x) \) は次のようになります。(複雑なので覚える必要はないです。上の定義でおさえておきましょう)
$$ f_X(x)=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}} \quad (-\infty<x<\infty) $$
ここで、 \( \Gamma(s) \) はガンマ関数であり、
$$ \Gamma(s)=\int_0^{\infty}x^{s-1}e^{-x}dx \quad (s>0) $$
で定義されます。(詳しい性質については微分積分学06をご覧ください。)
確率密度関数 \( f_X(x) \) のグラフを自由度 \( n \) ごとに表すと次のようになります。
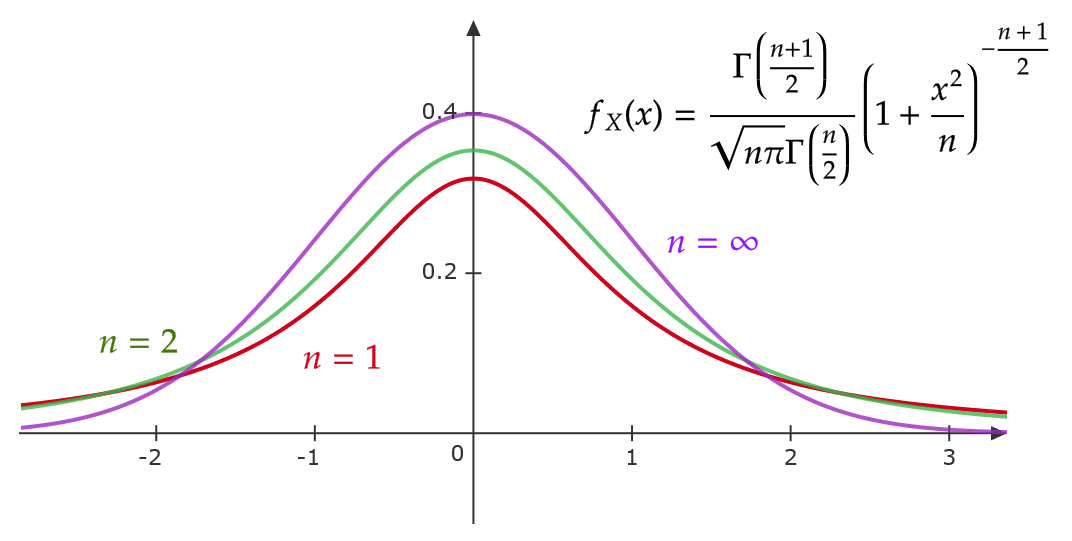
この確率密度関数 \( f_X(x) \) は \( x=0 \) を中心に左右対称となっています。
なぜ、この分布がスチューデントの \( t \) 分布とよばれているのかというと、スチューデントとは \( t \) 分布を発見したゴセットの論文におけるペンネームであり、その論文中で使用されている変数が \( t \) であったためであるとされています。(諸説あります)
自由度 \( n \) の \( t \) 分布 \( t(n) \) に従う確率変数 \( X \) の上側確率
$$ P(X≧x)=\alpha $$
となる \( x \) の値は \( t \) 分布表という表にまとめられています。
(\( t \) 分布表は確率・統計の参考書や問題集をご覧ください。このサイトでは東京大学出版会の統計学入門や統計検定2級の公式参考書の表を参考に計算しています。)
(1) 確率変数 \( X \) が自由度 \( 15 \) の \( t \) 分布 \( t(15) \) に従っているとする。
このとき、次の確率を求める。
$$ \begin{align} &P(1.341≦X≦2.602) \\ &=P(X≦2.602)-P(X≦1.341) \\ &=\{ 1-P(X≧2.602) \}-\{ 1-P(X≧1.341)\} \\ &=\{ 1-0.01\}-\{1-0.1\} \\ & (自由度15でt分布表を横にみて、2.602,1.341に一番近い\alphaをみつける) \\ &=0.09 \end{align} $$
(2) 確率変数 \( X,Y \) は互いに独立であり、 \( X \) は正規分布 \( N(3,4) \) に、 \( Y \) は自由度 \( 9 \) のカイ2乗分布 \( \chi^2(9) \) に従うとする。
このとき、確率
$$ P\left( \frac{3X-9}{2\sqrt{Y}}<-1.38 \right) $$
を求める。
まず、 \( \frac{X-3}{2} \) は標準正規分布 \( N(0,1) \) 、\( Y \) は自由度 \( 9 \) のカイ2乗分布 \( \chi^2(9) \) に従うので、 \( t \) 分布の定義より、
$$ \frac{\frac{X-3}{2}}{\sqrt{\frac{Y}{9}}}=\frac{3(X-3)}{2\sqrt{Y}}=\frac{3X-9}{2\sqrt{Y}} $$
は自由度 \( 9 \) の \( t \) 分布 \( t(9) \) に従う。
したがって、求める確率は
$$ \begin{align} &P\left( \frac{3X-9}{2\sqrt{Y}}<-1.38 \right) \\ &=P\left( \frac{3X-9}{2\sqrt{Y}}≧1.38 \right) \quad (確率密度関数が \ x=0 \ に関して対称) \\ &=0.1 \\ & (自由度9でt分布表を横にみて、1.38に一番近い\alphaをみつける) \end{align} $$
\( t \) 分布の性質として、次が成り立ちます。
確率変数 \( X \) が自由度 \( n \) の \( t \) 分布 \( t(n) \) に従っているとする。このとき、
(1) $$ \int_{-\infty}^{\infty}f_X(x)dx=\int_{-\infty}^{\infty}\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx=1 $$
(2) $$ E(X)=0, \quad V(X)=\frac{n}{n-2} \ (n≧3) $$
(3) 自由度 \( n \) を限りなく大きくするとき、自由度 \( n \) の \( t \) 分布 \( t(n) \) は標準正規分布 \( N(0,1) \) に限りなく近づく。
定理3の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} \int_{-\infty}^{\infty}f_X(x)dx&=\int_{-\infty}^{\infty}\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx \\ &=\frac{2\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx \quad (被積分関数は偶関数) \end{align} $$
ここで、変数変換
$$ y=\left(1+\frac{x^2}{n} \right)^{-1}, \quad dx=-\frac{1}{2}\sqrt{n}(1-y)^{-\frac{1}{2}}y^{-\frac{3}{2}}dy $$
を行うと、
$$ \begin{align} &\frac{2\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx \\ &=\frac{2\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_1^0\left(-\frac{1}{2}\right)\sqrt{n}y^{\frac{n-2}{2}}(1-y)^{-\frac{1}{2}}dy \\ &=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}\right)}\int_0^1y^{\frac{n}{2}-1}(1-y)^{\frac{1}{2}-1}dy \\ &=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}\right)}B\left(\frac{n}{2},\frac{1}{2} \right) \end{align} $$
ここで、 \( B(p,q) \) はベータ関数であり、
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx \quad (p,q>0) $$
で定義されます。
したがって、微分積分学06の定理9と微分積分学06の定理10(3)より、
$$ \begin{align} \int_{-\infty}^{\infty}f_X(x)dx&=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}\right)}B\left(\frac{n}{2},\frac{1}{2} \right) \\ &=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}\right)}\frac{\Gamma\left(\frac{3}{2}\right)\Gamma\left(\frac{n}{2}-1\right)}{\Gamma\left( \frac{n+1}{2} \right)} \\ &=\frac{\Gamma\left(\frac{1}{2}\right)}{\sqrt{\pi}}=1 \end{align} $$
(2) 確率変数 \( X \) が自由度 \( n \) の \( t \) 分布 \( t(n) \) に従っているとすると、
$$ \begin{align} E(X)&=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_{-\infty}^{\infty}x\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx \\ &=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_{\infty}^{-\infty}(-y)\left( 1+\frac{y^2}{n} \right)^{-\frac{n+1}{2}}(-1)dy \\ &(y=-x, \ dx=(-1)dy, \ 積分範囲に注意) \\ &=-\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_{-\infty}^{\infty}y\left( 1+\frac{y^2}{n} \right)^{-\frac{n+1}{2}}dy \\ &=-\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_{-\infty}^{\infty}x\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx \quad (yをxで置きなおした) \\ &=-E(X) \end{align} $$
したがって、 \( E(X)=0 \)
また、 \( n≧3 \) とするとき、
$$ \begin{align} E(X^2)&=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_{-\infty}^{\infty}x^2\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx \\ &=\frac{2\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}x^2\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx \quad (被積分関数は偶関数) \end{align} $$
ここで、変数変換
$$ y=\left(1+\frac{x^2}{n} \right)^{-1}, \quad dx=-\frac{1}{2}\sqrt{n}(1-y)^{-\frac{1}{2}}y^{-\frac{3}{2}}dy $$
を行うと、
$$ \begin{align} &\frac{2\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}x^2\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}}dx \\ &=\frac{2\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\int_1^0\left(\frac{n}{y}-n\right)\left(-\frac{1}{2}\right)\sqrt{n}y^{\frac{n-2}{2}}(1-y)^{-\frac{1}{2}}dy \\ &=\frac{n\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}\right)}\int_0^1y^{(\frac{n}{2}-1)-1}(1-y)^{\frac{3}{2}-1}dy \\ &=\frac{n\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}\right)}B\left(\frac{n}{2}-1,\frac{3}{2} \right) \end{align} $$
ここで、 \( B(p,q) \) はベータ関数であり、
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx \quad (p,q>0) $$
で定義されます。
したがって、微分積分学06の定理9と微分積分学06の定理8(1)と微分積分学06の定理10(3)より、
$$ \begin{align} E(X^2)&=\frac{n\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}\right)}B\left(\frac{n}{2}-1,\frac{3}{2} \right) \\ &=\frac{n\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{\pi}\Gamma\left(\frac{n}{2}\right)}\frac{\Gamma\left(\frac{3}{2}\right)\Gamma\left(\frac{n}{2}-1\right)}{\Gamma\left( \frac{n+1}{2} \right)} \\ &=\frac{\frac{n}{2}\Gamma\left(\frac{1}{2}\right)\Gamma\left(\frac{n}{2}-1\right)}{\sqrt{\pi}\left(\frac{n}{2}-1\right)\Gamma\left( \frac{n}{2}-1\right)}=\frac{n}{n-2} \end{align} $$
よって、
$$ \begin{align} V(X)&=E(X^2)-\{E(X)\}^2=\frac{n}{n-2} \end{align} $$
(3) 自由度 \( n \) の \( t \) 分布の確率密度関数を \( f_n(x) \) とおきます。つまり、
$$ f_n(x)=\frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\left( 1+\frac{x^2}{n} \right)^{-\frac{n+1}{2}} $$
まず、スターリングの公式をガンマ関数に拡張した公式
$$ \Gamma(z)≒\sqrt{2\pi}z^{z-\frac{1}{2}}e^{-z} $$
(この公式の詳細は省略します)
を用いると、確率密度関数の係数部分は次のように近似できます。
$$ \begin{align} \frac{\Gamma\left( \frac{n+1}{2} \right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}&≒\frac{\left(\frac{n+1}{2}\right)^{\frac{n+1}{2}-\frac{1}{2}}e^{-\frac{n+1}{2}}\sqrt{2\pi}}{\sqrt{n\pi}\left(\frac{n}{2}\right)^{\frac{n}{2}-\frac{1}{2}}e^{-\frac{n}{2}}\sqrt{2\pi}} \\ &=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}}\left(1+\frac{1}{n}\right)^{\frac{n}{2}} \\ &\to \frac{1}{\sqrt{2\pi}} \ (n\to\infty) \end{align} $$
また、
$$ \begin{align} \log \left(1+\frac{x^2}{n}\right)^{-\frac{n+1}{2}}&=\left(-\frac{n+1}{2}\right)\frac{x^2}{n}\cdot\log\left(1+\frac{x^2}{n}\right)^\frac{n}{x^2} \\ &\to -\frac{x^2}{2} \ (n\to\infty) \end{align} $$
したがって、これらを合わせると、
$$ \begin{align} \lim_{n\to\infty}f_n(x)&=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \end{align} $$
となり、標準正規分布 \( N(0,1) \) に限りなく近づく。
標本分布と \( t \) 分布との関係について、次が成り立ちます。
\( X_1,\cdots,X_n \) は互いに独立で正規分布 \( N(\mu,\sigma^2) \) に従うとする。
(つまり、 \( X_i \) は正規母集団 \( N(\mu,\sigma^2) \) からの標本であると考えられる)
また、 \( X_1,\cdots,X_n \) の標本平均を \( \overline{X} \) 、標本分散を \( S^2 \) とする。
このとき、
$$ \frac{\sqrt{n}(\overline{X}-\mu)}{S} $$
は自由度 \( n-1 \) の \( t \) 分布 \( t(n-1) \) に従う。
定理4の証明(気になる方だけクリックしてください)
まず、正規分布の再生性より、 \( \overline{X} \) は正規分布 \( N(\mu,\frac{\sigma^2}{n}) \) に従うので、標準化
$$ \frac{\overline{X}-\mu}{\frac{\sigma}{\sqrt{n}}}=\frac{\sqrt{n}(\overline{X}-\mu)}{\sigma} $$
は標準正規分布 \( N(0,1) \) に従います。
また、定理2(2)より、
$$ \sum_{i=1}^n\left( \frac{X_i-\overline{X}}{\sigma} \right)^2=\frac{(n-1)S^2}{\sigma^2} $$
は自由度 \( n-1 \) のカイ2乗分布 \( \chi^2(n-1) \) に従います。
したがって、 \( t \) 分布の定義より、
$$ \frac{\frac{\sqrt{n}(\overline{X}-\mu)}{\sigma}}{\sqrt{\frac{\frac{(n-1)S^2}{\sigma^2}}{n-1}}}=\frac{\sqrt{n}(\overline{X}-\mu)}{S} $$
は自由度 \( n-1 \) の \( t \) 分布 \( t(n-1) \) に従います。
F分布
確率変数 \( X,Y \) が互いに独立で \( X \) が自由度 \( m \) のカイ2乗分布 \( \chi^2(m) \) 、 \( Y \) が自由度 \( n \) のカイ2乗分布 \( \chi^2(n) \) に従うとします。このとき、
$$ F=\frac{\frac{X}{m}}{\frac{Y}{n}} $$
が従う確率分布を自由度 \( (m,n) \) の \( F \) 分布といい、 \( F(m,n) \) と表します。
確率変数 \( X \) が自由度 \( (m,n) \) の \( F \) 分布 \( F(m,n) \) に従うとき、確率密度関数 \( f_X(x) \) は次のようになります。(複雑なので覚える必要はないです。上の定義でおさえておきましょう)
$$ f_X(x)=\begin{cases} \frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\left(\frac{m}{n} \right)^{\frac{m}{2}}x^{\frac{m}{2}-1}\left(1+\frac{m}{n}x\right)^{-\frac{m+n}{2}} & (x>0) \\ 0 & (x≦0) \end{cases} $$
ここで、 \( \Gamma(s) \) はガンマ関数であり、
$$ \Gamma(s)=\int_0^{\infty}x^{s-1}e^{-x}dx \quad (s>0) $$
で定義されます。(詳しい性質については微分積分学06をご覧ください。)
確率密度関数 \( f_X(x) \) のグラフを自由度 \( (m,n) \) ごとに表すと次のようになります。
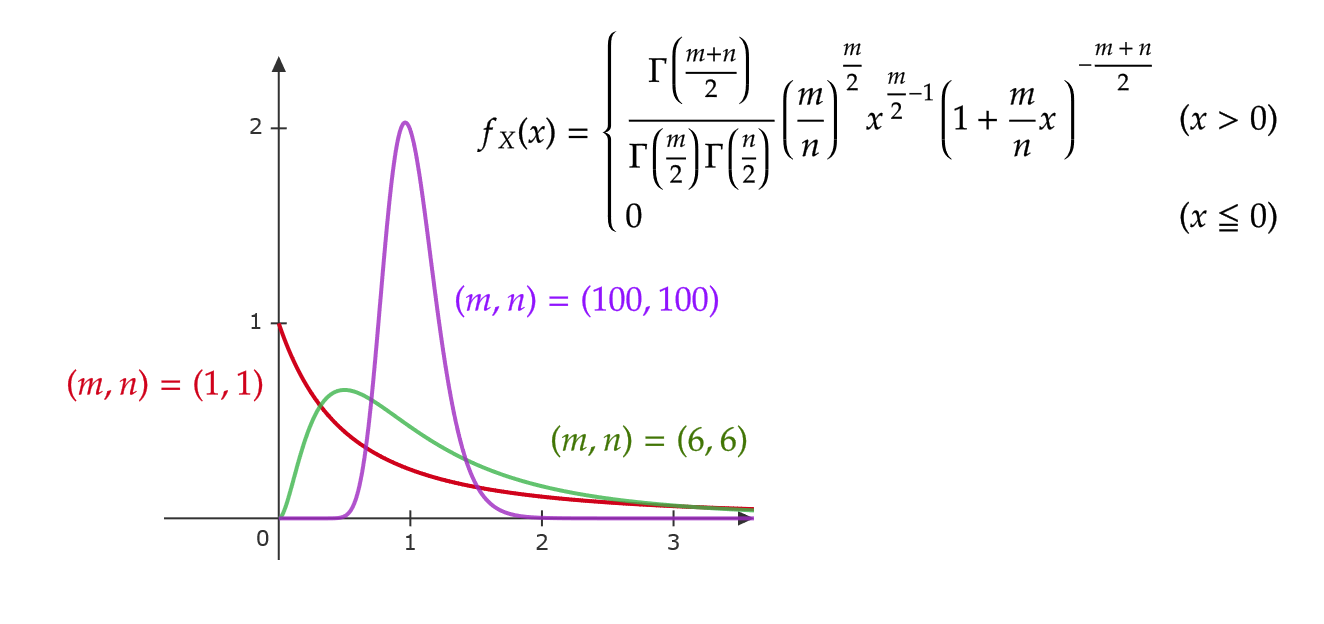
なぜ、この分布が \( F \) 分布とよばれているのかというと、 \( F \) 分布を発見したスネデカーがフィッシャーに敬意を表して頭文字の \( F \) をつけたためです。
自由度 \( (m,n) \) の \( F \) 分布 \( F(m,n) \) に従う確率変数 \( X \) の上側確率
$$ P(X≧x)=\alpha $$
となる \( x \) の値は \( F \) 分布表という表にまとめられています。
(\( F \) 分布表は確率・統計の参考書や問題集をご覧ください。このサイトでは東京大学出版会の統計学入門や統計検定2級の公式参考書の表を参考に計算しています。)
例は後に回して、まず\( F \) 分布の性質として次が成り立ちます。
確率変数 \( X \) が自由度 \( (m,n) \) の \( F \) 分布 \( F(m,n) \) に従っているとする。このとき、
(1) $$ \int_{-\infty}^{\infty}f_X(x)dx=\int_0^{\infty}\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\left(\frac{m}{n} \right)^{\frac{m}{2}}x^{\frac{m}{2}-1}\left(1+\frac{m}{n}x\right)^{-\frac{m+n}{2}}dx=1 $$
(2) $$ E(X)=\frac{n}{n-2} \ (n≧3), \quad V(X)=\frac{2n^2(m+n-2)}{m(n-2)^2(n-4)} \ (n≧5) $$
(3) 確率変数 \( \frac{1}{X} \) は自由度 \( (n,m) \) の \( F \) 分布 \( F(n,m) \) に従う。これより、
$$ P(X≧x)=P\left(\frac{1}{X}≦\frac{1}{x}\right)=1-P\left(\frac{1}{X}≧\frac{1}{x}\right) $$
(つまり、自由度 \( (m,n) \) の \( F \) 分布 \( F(m,n) \) に従っている確率変数 \( X \) の下側確率を求めたいときには、自由度 \( (n,m) \) の \( F \) 分布 \( F(n,m) \) の上側確率を考えればよい)
(4) 確率変数 \( Y \) が自由度 \( n \) の \( t \) 分布 \( t(n) \) に従っているとする。
このとき、確率変数 \( Y^2 \) は自由度 \( (1,n) \) の \( F \) 分布 \( F(1,n) \) に従う。
定理5の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} \int_{-\infty}^{\infty}f_X(x)dx&=\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\int_0^{\infty}\left(\frac{m}{n} \right)^{\frac{m}{2}}x^{\frac{m}{2}-1}\left(1+\frac{m}{n}x\right)^{-\frac{m+n}{2}}dx \end{align} $$
ここで、変数変換
$$ y=\left(1+\frac{m}{n}x \right)^{-1}, \quad dx=-\frac{n}{m}y^{-2}dy $$
を行うと、
$$ \begin{align} &\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\int_0^{\infty}\left(\frac{m}{n} \right)^{\frac{m}{2}}x^{\frac{m}{2}-1}\left(1+\frac{m}{n}x\right)^{-\frac{m+n}{2}}dx \\ &=\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\int_1^0\left(\frac{m}{n}\right)^{\frac{m}{2}}\left(\frac{n}{m}\right)^{\frac{m}{2}-1}y^{-\frac{m}{2}+1}(1-y)^{\frac{m}{2}-1}y^{\frac{m+n}{2}}\left(-\frac{n}{m}\right)y^{-2}dy \\ &=\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\int_0^1y^{\frac{n}{2}-1}(1-y)^{\frac{m}{2}-1}dy \\ &=\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}B\left(\frac{n}{2},\frac{m}{2} \right) \end{align} $$
ここで、 \( B(p,q) \) はベータ関数であり、
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx \quad (p,q>0) $$
で定義されます。
したがって、微分積分学06の定理9より、
$$ \begin{align} \int_{-\infty}^{\infty}f_X(x)dx&=\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}B\left(\frac{n}{2},\frac{m}{2} \right) \\ &=\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\cdot\frac{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}{\Gamma\left( \frac{m+n}{2}\right)}=1 \end{align} $$
(2) \( n≧3 \) とする。確率変数 \( X \) が自由度 \( (m,n) \) の \( F \) 分布 \( F(m,n) \) に従っているとすると、
$$ \begin{align} E(X)&=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\left(\frac{m}{n}\right)^{\frac{m}{2}}x^{\frac{m}{2}}\left( 1+\frac{m}{n}x \right)^{-\frac{m+n}{2}}dx \end{align} $$
ここで、変数変換
$$ y=\left(1+\frac{m}{n}x \right)^{-1}, \quad dx=-\frac{n}{m}y^{-2}dy $$
を行うと、
$$ \begin{align} &\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\left(\frac{m}{n}\right)^{\frac{m}{2}}x^{\frac{m}{2}}\left( 1+\frac{m}{n}x \right)^{-\frac{m+n}{2}}dx \\ &=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\int_1^0\left(\frac{m}{n}\right)^{\frac{m}{2}}\left(\frac{n}{m}\right)^{\frac{m}{2}}y^{-\frac{m}{2}}(1-y)^{\frac{m}{2}}y^{\frac{n+m}{2}}\left(-\frac{n}{m}\right)y^{-2}dy \\ &=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\int_0^1\left(\frac{n}{m}\right)y^{\frac{n}{2}-2}(1-y)^{\frac{m}{2}}dy \\ &=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\frac{n}{m}B\left(\frac{n}{2}-1,\frac{m}{2}+1 \right) \end{align} $$
ここで、 \( B(p,q) \) はベータ関数であり、
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx \quad (p,q>0) $$
で定義されます。
したがって、微分積分学06の定理9と微分積分学06の定理8(1)より、
$$ \begin{align} E(X)&=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\frac{n}{m}B\left(\frac{n}{2}-1,\frac{m}{2}+1 \right) \\ &=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\frac{n}{m}\frac{\Gamma\left(\frac{m}{2}+1\right)\Gamma\left(\frac{n}{2}-1\right)}{\Gamma\left( \frac{m+n}{2} \right)} \\ &=\frac{n}{m}\frac{\frac{m}{2}\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}-1\right)}{\Gamma\left(\frac{m}{2}\right)\left(\frac{n}{2}-1\right)\Gamma\left( \frac{n}{2}-1\right)}=\frac{n}{m}\frac{m}{2}\frac{2}{n-2}=\frac{n}{n-2} \end{align} $$
また、 \( n≧5 \) とすると、
$$ \begin{align} E(X^2)&=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\left(\frac{m}{n}\right)^{\frac{m}{2}}x^{\frac{m}{2}+1}\left( 1+\frac{m}{n}x \right)^{-\frac{m+n}{2}}dx \end{align} $$
ここで、変数変換
$$ y=\left(1+\frac{m}{n}x \right)^{-1}, \quad dx=-\frac{n}{m}y^{-2}dy $$
を行うと、
$$ \begin{align} &\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\int_0^{\infty}\left(\frac{m}{n}\right)^{\frac{m}{2}}x^{\frac{m}{2}+1}\left( 1+\frac{m}{n}x \right)^{-\frac{m+n}{2}}dx \\ &=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\int_1^0\left(\frac{m}{n}\right)^{\frac{m}{2}}\left(\frac{n}{m}\right)^{\frac{m}{2}+1}y^{-\frac{m}{2}-1}(1-y)^{\frac{m}{2}+1}y^{\frac{n+m}{2}}\left(-\frac{n}{m}\right)y^{-2}dy \\ &=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\int_0^1\left(\frac{n}{m}\right)^2y^{\frac{n}{2}-3}(1-y)^{\frac{m}{2}+1}dy \\ &=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{n}{m}\right)^2B\left(\frac{n}{2}-2,\frac{m}{2}+2 \right) \end{align} $$
ここで、 \( B(p,q) \) はベータ関数であり、
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx \quad (p,q>0) $$
で定義されます。
したがって、微分積分学06の定理9と微分積分学06の定理8(1)より、
$$ \begin{align} E(X^2)&=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{n}{m}\right)^2B\left(\frac{n}{2}-2,\frac{m}{2}+2 \right) \\ &=\frac{\Gamma\left( \frac{m+n}{2} \right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{n}{m}\right)^2\frac{\Gamma\left(\frac{m}{2}+2\right)\Gamma\left(\frac{n}{2}-2\right)}{\Gamma\left( \frac{m+n}{2} \right)} \\ &=\left(\frac{n}{m}\right)^2\frac{\frac{m}{2}\left(\frac{m}{2}+1\right)\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}-2\right)}{\Gamma\left(\frac{m}{2}\right)\left(\frac{n}{2}-1\right)\left(\frac{n}{2}-2\right)\Gamma\left( \frac{n}{2}-2\right)} \\ &=\frac{n^2}{m^2}\frac{m}{2}\frac{m+2}{2}\frac{2}{n-2}\frac{2}{n-4}=\frac{n^2(m+2)}{m(n-2)(n-4)} \end{align} $$
より、
$$ \begin{align} V(X)&=E(X^2)-\{E(X)\}^2=\frac{n^2(m+2)}{m(n-2)(n-4)}-\frac{n^2}{(n-2)^2} \\ &=\frac{2n^2(m+n-2)}{m(n-2)^2(n-4)} \end{align} $$
(3) 確率変数 \( X \) が自由度 \( (m,n) \) の \( F \) 分布 \( F(m,n) \) に従っているとします。
\( Y=\frac{1}{X} \) とおくと、確率変数の変数変換によって \( Y \) の確率密度関数 \( f_Y(y) \) は次のようになることが知られています。
\( 0<y<\infty \) に対して、
$$ \begin{align} f_Y(y)&=f_X\left(\frac{1}{y}\right)\left|\frac{dx}{dy}\right|=f_X\left(\frac{1}{y}\right)\cdot y^{-2} \\ &=\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\left(\frac{1}{y}\right)^{\frac{m}{2}-1}\left(1+\frac{m}{n}\frac{1}{y}\right)^{-\frac{m+n}{2}}y^{-2} \\ &=\frac{\Gamma\left( \frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left( \frac{n}{2} \right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}y^{-\frac{m}{2}-1}\left(\frac{m}{n}\right)^{-\frac{m+n}{2}}\left(\frac{1}{y}\right)^{-\frac{m+n}{2}}\left(1+\frac{n}{m}y\right)^{-\frac{m+n}{2}} \\ &=\frac{\Gamma\left( \frac{n+m}{2}\right)}{\Gamma\left(\frac{n}{2}\right)\Gamma\left( \frac{m}{2} \right)}\left(\frac{n}{m} \right)^{\frac{n}{2}}y^{\frac{n}{2}-1}\left(1+\frac{n}{m}y\right)^{-\frac{n+m}{2}} \end{align} $$
したがって、 \( Y=\frac{1}{X} \) は自由度 \( (n,m) \) の \( F \) 分布 \( F(n,m) \) に従う。
(4) 確率変数 \( Y \) が自由度 \( n \) の \( t \) 分布 \( t(n) \) に従っているとします。
\( Z=Y^2 \) とおくと、分布関数を用いることにより、 \( Z \) の確率密度関数 \( f_Z(z) \) は次のようになります。
( \( Z=Y^2 \) の場合は逆変換が存在しないため、確率変数の変数変換は使えません)
\( 0<z<\infty \) に対して、微分積分学06の定理10(3)より、
$$ \begin{align} f_Z(z)&=\frac{d}{dz}P(Z≦z)=\frac{d}{dz}P(Y^2≦z) \\ &=\frac{d}{dz}P(-\sqrt{z}≦Y≦\sqrt{z}
)=\frac{d}{dz}\int_{-\sqrt{z}}^{\sqrt{z}}f_Y(y)dy \\ &=\frac{1}{2\sqrt{z}}f_Y(\sqrt{z})+\frac{1}{2\sqrt{z}}f_Y(-\sqrt{z}) \\ &=\frac{1}{2\sqrt{z}}f_Y(\sqrt{z})+\frac{1}{2\sqrt{z}}f_Y(\sqrt{z}) \quad (f_Y(y)は偶関数) \\ &=\frac{1}{\sqrt{z}}f_Y(\sqrt{z}) \\ &=\frac{\Gamma\left( \frac{n+1}{2}\right)}{\sqrt{n\pi}\Gamma\left(\frac{n}{2}\right)}\left(1+\frac{z}{n}\right)^{-\frac{n+1}{2}}z^{-\frac{1}{2}} \\ &=\frac{\Gamma\left( \frac{1+n}{2}\right)}{\Gamma\left(\frac{1}{2}\right)\Gamma\left( \frac{n}{2} \right)}\left(\frac{1}{n} \right)^{\frac{1}{2}}z^{\frac{1}{2}-1}\left(1+\frac{1}{n}z\right)^{-\frac{1+n}{2}} \end{align} $$
したがって、 \( Z=Y^2 \) は自由度 \( (1,n) \) の \( F \) 分布 \( F(1,n) \) に従う。
確率変数 \( X \) が自由度 \( (3,5) \) の \( F \) 分布 \( F(3,5) \) に従っているとする。
このとき、次の \( x,y \) の値を求める。
$$ P(x≦X)=0.025, \quad P(X<y)=0.05 $$
まず、 \( \alpha=0.025 \) の \( F \) 分布表を選び、自由度 \( (3,5) \) の交差するところを見ると、
$$ P(7.764≦X)=0.025 $$
となるので、 \( x=7.764 \)
次に、 \( y \) を求めるが、このままだと \( F \) 分布表にのっていないので定理5(3)を利用する。
つまり、 \( \frac{1}{X} \) は自由度 \( (5,3) \) の \( F \) 分布 \( F(5,3) \) に従うことになり、さらに
$$ P(X<y)=P\left( \frac{1}{X}≧\frac{1}{y}\right)=0.05 $$
となるので、 \( \alpha=0.05 \) の \( F \) 分布表を選び、自由度 \( (5,3) \) の交差するところを見ると、
$$ P\left( \frac{1}{X}≧9.013\right)=0.05 $$
となるので、 \( y=\frac{1}{9.013}≒0.111 \)
標本分布と \( F \) 分布との関係について、次が成り立ちます。
\( X_1,\cdots,X_{n_1} \) は互いに独立で正規分布 \( N(\mu_1,\sigma_1^2) \) に従い、 \( Y_1,\cdots,Y_{n_2} \) は互いに独立で正規分布 \( N(\mu_2,\sigma_2^2) \) に従うとする。
(つまり、 \( X_i \) は正規母集団 \( N(\mu_1,\sigma_1^2) \) 、 \( Y_i \) は正規母集団 \( N(\mu_2,\sigma_2^2) \) からの標本であると考えられる)
また、 \( X_1,\cdots,X_{n_1} \) の標本平均を \( \overline{X} \) 、標本分散を \( S_1^2 \) 、 \( Y_1,\cdots,Y_{n_2} \) の標本平均を \( \overline{Y} \) 、標本分散を \( S_2^2 \) とする。
このとき、
$$ \frac{\frac{S_1^2}{\sigma^2_1}}{\frac{S_2^2}{\sigma^2_2}}=\frac{S_1^2}{\sigma_1^2}\cdot \frac{\sigma^2_2}{S_2^2} $$
は自由度 \( (n_1-1,n_2-1) \) の \( F \) 分布 \( F(n_1-1,n_2-1) \) に従う。
定理6の証明(気になる方だけクリックしてください)
定理2(2)より、
$$ \sum_{i=1}^{n_1}\left( \frac{X_i-\overline{X}}{\sigma_1} \right)^2=\frac{(n_1-1)S_1^2}{\sigma_1^2} $$
は自由度 \( n_1-1 \) のカイ2乗分布 \( \chi^2(n_1-1) \) に従い、
$$ \sum_{j=1}^{n_2}\left( \frac{Y_j-\overline{Y}}{\sigma_2} \right)^2=\frac{(n_2-1)S_2^2}{\sigma_2^2} $$
は自由度 \( n_2-1 \) のカイ2乗分布 \( \chi^2(n_2-1) \) に従います。
したがって、 \( F \) 分布の定義より、
$$ \frac{\frac{\frac{(n_1-1)S_1^2}{\sigma_1^2}}{n_1-1}}{\frac{\frac{(n_2-1)S_2^2}{\sigma_2^2}}{n_2-1}}=\frac{\frac{S_1^2}{\sigma^2_1}}{\frac{S_2^2}{\sigma^2_2}}=\frac{S_1^2}{\sigma_1^2}\cdot \frac{\sigma^2_2}{S_2^2} $$
は自由度 \( (n_1-1,n_2-1) \) の \( F \) 分布 \( F(n_1-1,n_2-1) \) に従います。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

