こんにちは、ひかりです。
今回は確率・統計から正規分布について解説していきます。
この記事では以下のことを紹介します。
- 正規分布について
- 対数正規分布について
- 2次元正規分布について
正規分布
正規分布
ここでは、確率・統計においてもっとも重要といっても過言ではない正規分布について考えてみましょう。
連続型確率変数 \( X \) の確率密度関数 \( f_X(x) \) が
$$ f_X(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$
となるとき、 \( X \) が従う確率分布を正規分布といい、 \( N(\mu,\sigma^2) \) と表します。
この分布は応用上いたるところに現れる確率分布となっているため、「ありふれた」・「通常の」という意味の正規(normal)という言葉でよばれるようになりました。
この分布の確率密度関数 \( f_X(x) \) のグラフは次のようになります。
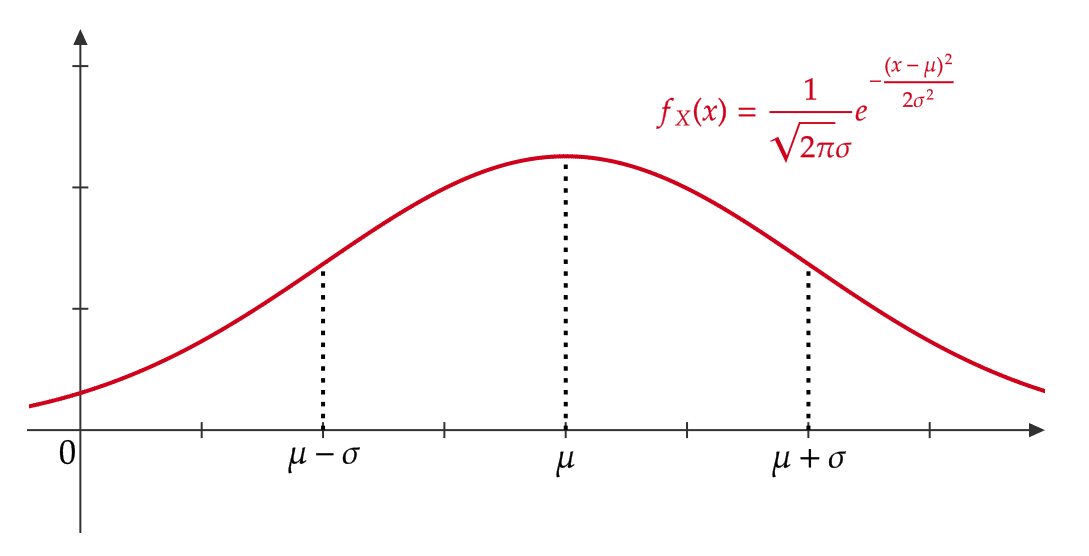
このグラフから正規分布の確率密度関数には次のような性質があることが分かります。
正規分布 \( N(\mu,\sigma^2) \) の確率密度関数 \( f_X(x) \) のグラフに関して次が成り立つ。
(1) \( y=f_X(x) \) は \( x=\mu \) に関して対称で釣り鐘型の形をしている。
(2) \( y=f_X(x) \) は \( x=\mu \) で極大値(かつ最大値)をもつ。
(3) \( y=f_X(x) \) は \( x=\mu\pm \sigma \) で変曲点をもち、区間 \( (\mu-\sigma,\mu+\sigma) \) で上に凸、区間 \( (-\infty,\mu-\sigma) \) かつ区間 \( (\mu+\sigma,+\infty) \) で下に凸である。
そのほか正規分布の性質として、次が成り立ちます。
確率変数 \( X \) が正規分布 \( N(\mu,\sigma^2) \) に従っているとする。このとき、
(1) $$ \int_{-\infty}^{\infty}f_X(x)dx=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx=1 $$
(2) $$ E(X)=\mu, \quad V(X)=\sigma^2 $$
(3) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=e^{\mu t+\frac{\sigma^2t^2}{2}} $$
(4) (正規分布の再生性) 確率変数 \( Y \) が正規分布 \( N(m,s^2) \) に従っているとする。
また、 \( X \) と \( Y \) が独立であるとする。
このとき、 \( X+Y \) は正規分布 \( N(\mu+m,\sigma^2+s^2) \) に従う。
定理2の証明(気になる方だけクリックしてください)
(1) $$ I=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx $$
とおくと、
$$ \begin{align} I^2&=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y-\mu)^2}{2\sigma^2}}dy \\ &=\frac{1}{2\pi\sigma^2}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}e^{-\frac{s^2+t^2}{2\sigma^2}}dsdt \quad (s=x-\mu, \ t=y-\mu) \end{align} $$
極座標変換 \( s=r\cos \theta, \ t=r\sin\theta \) をすると、
$$ \begin{align} I^2=\frac{1}{2\pi \sigma^2}\int_0^{2\pi}d\theta \int_0^{\infty}e^{-\frac{r^2}{2\sigma^2}}rdr=\left[ -e^{-\frac{r^2}{2\sigma^2}}\right]^{\infty}_0=1 \end{align} $$
したがって、 \( I>0 \) より、 \( I=1 \) となります。
(2) $$ \begin{align} E(X)&=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}xe^{-\frac{(x-\mu)^2}{2\sigma^2}}dx \\ &=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}(\mu+\sigma y)e^{-\frac{y^2}{2}}dy \quad (y=\frac{x-\mu}{\sigma}, \ dy=\frac{dx}{\sigma}) \\ &=\frac{\mu}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-\frac{y^2}{2}}dy+\frac{\sigma}{\sqrt{2\pi}}\int_{-\infty}^{\infty}ye^{-\frac{y^2}{2}}dy \\ &=\frac{\mu}{\sqrt{2\pi}}\sqrt{2\pi}+\frac{\sigma}{\sqrt{2\pi}}\left[ -e^{-\frac{y^2}{2}} \right]^{\infty}_{-\infty}=\mu, \end{align} $$
$$ \begin{align} V(X)&=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}(x-\mu)^2e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx \\ &=\frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty}y^2e^{-\frac{y^2}{2}}dy \quad (y=\frac{x-\mu}{\sigma}, \ dy=\frac{dx}{\sigma}) \\ &=\frac{\sigma^2}{\sqrt{2\pi}}\left( -\left[ ye^{-\frac{y^2}{2}} \right]^{\infty}_{-\infty}+\int^{\infty}_{-\infty} e^{-\frac{y^2}{2}}dy \right)=\sigma^2 \end{align} $$
(3) $$ \begin{align} M_X(t)&=E(e^{tX})=\frac{1}{\sqrt{2\pi}\sigma}\int^{\infty}_{-\infty}e^{tx}e^{-\frac{(x-\mu)^2}{2\sigma^2}}dx \\ &=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{-\frac{1}{2\sigma^2}\{ (x-\mu)^2-2\sigma^2tx\}}dx \\ &=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{-\frac{1}{2\sigma^2}\{ (x-(\mu+\sigma^2t))^2-(2\sigma^2\mu t+\sigma^4t^2)\}}dx \\ &=\frac{1}{\sqrt{2\pi}\sigma}e^{\mu t+\frac{\sigma^2}{2}t^2}\int_{-\infty}^{\infty}e^{-\frac{1}{2}\left( \frac{x-(\mu+\sigma^2 t)}{\sigma}\right)^2} \\ &=\frac{1}{\sqrt{2\pi}\sigma}e^{\mu t+\frac{\sigma^2}{2}t^2}\int_{-\infty}^{\infty}e^{-\frac{y^2}{2}}\sigma dy \quad (y=\frac{x-(\mu+\sigma^2t)}{\sigma}, \ dy=\frac{dx}{\sigma}) \\ &=\frac{1}{\sqrt{2\pi}}e^{\mu t+\frac{\sigma^2}{2}t^2}\sqrt{2\pi}=e^{\mu t+\frac{\sigma^2t^2}{2}} \end{align} $$
(4) \( X \) のモーメント母関数は \( e^{\mu t+\frac{\sigma^2t^2}{2}} \) 、 \( Y \) のモーメント母関数は \( e^{mt+\frac{s^2t^2}{2}} \) である。
このとき、 \( X+Y \) のモーメント母関数は \( X \) と \( Y \) は独立であるので、確率・統計09の定理3のあとの注意より、
$$ \begin{align} M_{X+Y}(t)&=E(e^{X+Y})=E(e^Xe^Y) \\ &=E(e^X)E(e^Y) \quad (XとYは独立であることより) \\ &=e^{\mu t+\frac{\sigma^2t^2}{2}}e^{mt+\frac{s^2t^2}{2}}=e^{(\mu+m)t+\frac{(\sigma^2+s^2)t^2}{2}} \end{align} $$
したがって、 \( X+Y \) は \( N(\mu+m,\sigma^2+s^2) \) に従う。
例を見ていく前に、確率・統計08の例6で扱った確率変数の標準化を振り返ります。
確率変数 \( X \) が正規分布 \( N(\mu,\sigma^2) \) に従うとき、定理2より平均 \( \mu \) 、分散 \( \sigma^2 \) であるので、
$$ Z=\frac{X-\mu}{\sigma} $$
と標準化をすると、 \( Z \) は平均 \( 0 \) 、分散 \( 1 \) の正規分布 \( N(0,1) \) に従うことになります。
この \( N(0,1) \) の分布関数
$$ \Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^xe^{-\frac{t^2}{2}}dt $$
は初等関数で表すことができないので、 \( \Phi(x) \) の値は正規分布表という表にまとめられています。
(正規分布表は確率・統計の参考書や問題集をご覧ください。このサイトでは東京大学出版会の統計学入門や統計検定2級の公式参考書の表(上側確率(つまり、 \( 1-\Phi(x) \) の表)を参考に計算しています。)
(1) ある高校の1年生男子の身長の分布は平均 \( 167 \) cm、標準偏差 \( 7 \) cmの正規分布に従うということがわかった。
このとき、身長が \( 160 \) cm以上 \( 172 \) cm以下の生徒はおよそ何%いるのかを求める。
その高校の1年生男子の身長を \( X \) とすると、 \( X \) は正規分布 \( N(167,7^2) \) に従う。
よって、 \( \displaystyle Z=\frac{X-167}{7} \) とすると、 \( Z \) は \( N(0,1) \) に従う。
したがって、求める確率は
$$ \begin{align} &P(160≦X≦172) \\ &=P\left( \frac{160-167}{7}≦\frac{X-167}{7}≦\frac{172-167}{7} \right) \\ &=P\left(-1≦Z≦\frac{5}{7}\right) \\ &≒P(-1≦Z≦0.71) \\ &=P(Z≦0.71)-P(Z≦-1) \\ &=P(Z≦0.71)-P(Z≧1) \quad (確率密度関数が \ x=0 \ に関して対称) \\ &=\{ 1-P(Z≧0.71) \}-P(Z≧1) \\ &=\{ 1-0.23885\}-0.15866 \quad (正規分布表をみて値を入れる) \\ &=0.60249 \end{align} $$
(これらの計算は確率がその範囲における確率密度関数の面積であるということを頭に思い浮かべるとわかりやすい)
よって、約60%いることがわかる。
(2) 確率変数 \( X \) が正規分布 \( N(\mu,\sigma^2) \) に従っているとする。
つまり、 \( \displaystyle Z=\frac{X-\mu}{\sigma} \) とすると、 \( Z \) は \( N(0,1) \) に従う。
このとき、次の3つの確率を求める。
$$ \begin{align} &P(\mu-\sigma≦X≦\mu+\sigma) \\ &=P\left( \frac{(\mu-\sigma)-\mu}{\sigma}≦\frac{X-\mu}{\sigma}≦\frac{(\mu+\sigma)-\mu}{\sigma} \right) \\ &=P(-1≦Z≦1) \\ &=P(Z≦1)-P(Z≦-1) \\ &=P(Z≦1)-P(Z≧1) \quad (確率密度関数が \ x=0 \ に関して対称) \\ &=\{ 1-P(Z≧1) \}-P(Z≧1) \\ &=\{ 1-0.15866\}-0.15866 \quad (正規分布表をみて値を入れる) \\ &=0.68268 \end{align} $$
$$ \begin{align} &P(\mu-2\sigma≦X≦\mu+2\sigma) \\ &=P\left( \frac{(\mu-2\sigma)-\mu}{\sigma}≦\frac{X-\mu}{\sigma}≦\frac{(\mu+2\sigma)-\mu}{\sigma} \right) \\ &=P(-2≦Z≦2) \\ &=P(Z≦2)-P(Z≦-2) \\ &=P(Z≦2)-P(Z≧2) \quad (確率密度関数が \ x=0 \ に関して対称) \\ &=\{ 1-P(Z≧2) \}-P(Z≧2) \\ &=\{ 1-0.02275\}-0.02275 \quad (正規分布表をみて値を入れる) \\ &=0.9545 \end{align} $$
$$ \begin{align} &P(\mu-3\sigma≦X≦\mu+3\sigma) \\ &=P\left( \frac{(\mu-3\sigma)-\mu}{\sigma}≦\frac{X-\mu}{\sigma}≦\frac{(\mu+3\sigma)-\mu}{\sigma} \right) \\ &=P(-3≦Z≦3) \\ &=P(Z≦3)-P(Z≦-3) \\ &=P(Z≦3)-P(Z≧3) \quad (確率密度関数が \ x=0 \ に関して対称) \\ &=\{ 1-P(Z≧3) \}-P(Z≧3) \\ &=\{ 1-0.00134\}-0.00134 \quad (正規分布表をみて値を入れる) \\ &=0.99732 \end{align} $$
このことから、任意の正規分布 \( N(\mu,\sigma^2) \) において \( X \) は区間 \( [\mu-\sigma,\mu+\sigma] \) に約68.3%、区間 \( [\mu-2\sigma,\mu+2\sigma] \) に約95.4%、区間 \( [\mu-3\sigma,\mu+3\sigma] \) に約99.7%が入ることが分かる。
これらの区間のことをそれぞれ1シグマ範囲、2シグマ範囲、3シグマ範囲という。
標準正規分布
先ほどから出てきましたが、正規分布において、特に \( \mu=0,\sigma^2=1 \) である分布 \( N(0,1) \) のことを標準正規分布といいます。
連続型確率変数 \( X \) が標準正規分布 \( N(0,1) \) に従うとき、確率密度関数 \( f_X(x) \) は次のようになります。
$$ f_X(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} $$
標準正規分布の性質は、定理2で \( \mu=0,\sigma^2=1 \) としたものが成り立ちます。
確率変数 \( X \) が標準正規分布 \( N(0,1) \) に従っているとする。このとき、
(1) $$ \int_{-\infty}^{\infty}f_X(x)dx=\int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx=1 $$
(2) $$ E(X)=0, \quad V(X)=1 $$
(3) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=e^{\frac{t^2}{2}} $$
対数正規分布
年収や株価の収益率など、特に数理ファイナンスにおいてよく用いられている確率分布について紹介します。
連続型確率変数 \( X \) の確率密度関数 \( f_X(x) \) が
$$ f_X(x)=\begin{cases} \displaystyle \frac{1}{\sqrt{2\pi}\sigma x}e^{-\frac{(\log x-\mu)^2}{2\sigma^2}} & (x>0) \\ 0 & (x≦0) \end{cases} $$
となるとき、 \( X \) が従う確率分布を対数正規分布といい、 \( LN(\mu,\sigma^2) \) と表します。
これがなぜ対数正規分布とよばれるかというと、 \( X \) が対数正規分布 \( LN(\mu,\sigma^2) \) に従うとき、対数をとった \( \log X \) が正規分布 \( N(\mu,\sigma^2) \) に従うことがいえるからです。(定理4(3)をご覧ください。)
確率変数 \( X \) が対数正規分布 \( LN(\mu,\sigma^2) \) に従っているとする。このとき、
(1) $$ \int_{-\infty}^{\infty}f_X(x)dx=\int_{0}^{\infty}\frac{1}{\sqrt{2\pi}\sigma x}e^{-\frac{(\log x-\mu)^2}{2\sigma^2}}dx=1 $$
(2) $$ E(X)=e^{\mu+\frac{\sigma^2}{2}}, \quad V(X)=(e^{\sigma^2}-1)e^{2\mu+\sigma^2} $$
(3) \( \log X \) は正規分布 \( N(\mu,\sigma^2) \) に従う。
定理4の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} \int_{-\infty}^{\infty}f_X(x)dx&=\int_{0}^{\infty}\frac{1}{\sqrt{2\pi}\sigma x}e^{-\frac{(\log x-\mu)^2}{2\sigma^2}}dx \\ &=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{-t}e^{-\frac{(t-\mu)^2}{2\sigma^2}}e^tdt \quad (t=\log x, \ dx=e^tdt, \ 積分範囲に注意) \\ &=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt \\ &=1 \quad (正規分布の確率密度関数の積分なので1) \end{align} $$
(2) $$ \begin{align} E(X)&=\int_{-\infty}^{\infty}xf_X(x)dx=\int_0^{\infty}x\frac{1}{\sqrt{2\pi}\sigma x}e^{-\frac{(\log x-\mu)^2}{2\sigma^2}}dx \\ &=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{t-\frac{1}{2\sigma^2}(t^2-2\mu t+\mu^2)}dt \quad (t=\log x, \ dx=e^tdt, \ 積分範囲に注意) \\ &=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{-\frac{1}{2\sigma^2}(t^2-2(\mu+\sigma^2)t+\mu^2)}dt \\ &=\frac{1}{\sqrt{2\pi}\sigma}e^{\mu+\frac{\sigma^2}{2}}\int_{-\infty}^{\infty}e^{-\frac{1}{2\sigma^2}(t-(\mu+\sigma^2))^2}dt \\ &=e^{\mu+\frac{\sigma^2}{2}}\times \frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{-\frac{1}{2}\frac{(s-\mu)^2}{\sigma^2}}ds \quad (s=t-\sigma^2) \\ &=e^{\mu+\frac{\sigma^2}{2}} \quad (\times 以降は正規分布の確率密度関数の積分なので1) \end{align} $$
また、
$$ \begin{align} E(X^2)&=\int_{-\infty}^{\infty}x^2f_X(x)dx=\int_0^{\infty}x^2\frac{1}{\sqrt{2\pi}\sigma x}e^{-\frac{(\log x-\mu)^2}{2\sigma^2}}dx \\ &=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{2t-\frac{1}{2\sigma^2}(t^2-2\mu t+\mu^2)}dt \quad (t=\log x, \ dx=e^tdt, \ 積分範囲に注意) \\ &=\frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{-\frac{1}{2\sigma^2}(t^2-2(\mu+2\sigma^2)t+\mu^2)}dt \\ &=\frac{1}{\sqrt{2\pi}\sigma}e^{2\mu+2\sigma^2}\int_{-\infty}^{\infty}e^{-\frac{1}{2\sigma^2}(t-(\mu+2\sigma^2))^2}dt \\ &=e^{2\mu+2\sigma^2}\times \frac{1}{\sqrt{2\pi}\sigma}\int_{-\infty}^{\infty}e^{-\frac{1}{2}\frac{(s-\mu)^2}{\sigma^2}}ds \quad (s=t-2\sigma^2) \\ &=e^{2\mu+2\sigma^2} \quad (\times 以降は正規分布の確率密度関数の積分なので1) \end{align} $$
より、
$$ \begin{align} V(X)&=E(X^2)-\{ E(X) \}^2=e^{2\mu+2\sigma^2}-\left(e^{\mu+\frac{\sigma^2}{2}}\right)^2=(e^{\sigma^2}-1)e^{2\mu+\sigma^2} \end{align} $$
(3) \( Y=\log X \) とおくと、確率変数の変数変換によって \( Y \) の確率密度関数 \( f_Y(y) \) は次のようになることが知られています。
\( -\infty<y<\infty \) に対して、
$$ \begin{align} f_Y(y)&=f_X(e^y)\left|\frac{dx}{dy}\right|=f_X(e^y)\cdot e^y \\ &=\frac{1}{\sqrt{2\pi}\sigma e^y}e^{-\frac{(\log (e^y)-\mu)^2}{2\sigma^2}}\cdot e^y \quad (e^y>0より) \\ &=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(y-\mu)^2}{2\sigma^2}} \end{align} $$
したがって、 \( Y=\log X \) は正規分布 \( N(\mu,\sigma^2) \) に従います。
2次元正規分布
一般にデータというのは複数個考えることが多いです。(確率・統計02の記事で2変数のデータを扱いました。)
すると、確率変数もおのずと複数個考えることになり、確率分布も多次元化します。
複数個の確率分布の一般的な性質については確率・統計09の記事をご覧ください。
ここでは、話を簡単にするため2次元の正規分布について考えてみましょう。
連続型確率変数 \( X \) が正規分布 \( N(\mu_1,\sigma^2_1) \) に、連続型確率変数 \( Y \) が正規分布 \( N(\mu_2,\sigma^2_2) \) に従うとします。
そして、 \( X \) と \( Y \) の相関係数を \( \rho \) とおきます。
このとき、 \( X \) と \( Y \) の同時確率密度関数 \( f_{(X,Y)}(x,y) \) は次のようになります。
$$ f_{(X,Y)}(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}e^{-\frac{1}{2}\frac{1}{1-\rho^2}Q} $$
$$ Q=\left( \frac{x-\mu_1}{\sigma_1} \right)^2-2\rho \frac{x-\mu_1}{\sigma_1}\frac{y-\mu_2}{\sigma_2}+\left( \frac{y-\mu_2}{\sigma_2} \right)^2 $$
(証明についてはここでは省略します)
よって、この同時確率密度関数をもつとき、 \( (X,Y) \) が従う確率分布を2次元正規分布といい、 \( N(\mu_1,\mu_2,\sigma^2_1,\sigma^2_2,\rho) \) または \( N(\overrightarrow{\mu},V) \) と表します。
ここで、
$$ \overrightarrow{\mu}=\begin{pmatrix} \mu_1 \\ \mu_2 \end{pmatrix}, \quad V=\begin{pmatrix} \sigma^2_1 & \rho \sigma_1\sigma_2 \\ \rho \sigma_1\sigma_2 & \sigma^2_2 \end{pmatrix} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

