こんにちは、ひかりです。
今回は確率・統計から一様分布と指数分布について解説していきます。
この記事では以下のことを紹介します。
- 一様分布について
- 指数分布について
一様分布
一様分布
離散一様分布を連続化した確率分布について考えてみましょう。
連続型確率変数 \( X \) の確率密度関数 \( f_X(x) \) が
$$ f_X(x)=\begin{cases} \frac{1}{b-a} & (a≦x≦b) \\ 0 & (その他) \end{cases} $$
となるとき、 \( X \) が従う確率分布を一様分布といい、 \( U(a,b) \) と表します。
ある正の実数 \( x \) に対して小数第一位を四捨五入した数を考えて、もとの実数から四捨五入した数を引いた誤差を \( X \) とする。
(例えば、 \( x=2.34 \) とすると、小数第一位を四捨五入した数は \( 2 \) なので、 \( X=2.34-2=0.34 \) )
このとき、その誤差が \( 0≦X≦0.1 \) である確率を求める。
\( X \) は一様分布 \( U(-0.5,0.5) \) に従うので、
$$ P(0≦X≦0.1)=\int_0^{0.1}1dx=[x]^{0.1}_0=0.1 $$
一様分布の性質として、次が成り立ちます。
確率変数 \( X \) が一様分布 \( U(a,b) \) に従っているとする。このとき、
(1) $$ E(X)=\frac{a+b}{2}, \quad V(X)=\frac{(b-a)^2}{12} $$
(2) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=\frac{e^{bt}-e^{at}}{(b-a)t} $$
定理1の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} E(X)&=\int_{-\infty}^{\infty}xf(x)dx=\int_a^bx\frac{1}{b-a}dx \quad (x\not\in[a,b]ではf(x)=0) \\ &=\frac{1}{b-a}\left[ \frac{1}{2}x^2 \right]_a^b=\frac{b^2-a^2}{2(b-a)}=\frac{a+b}{2} \end{align} $$
また、
$$ \begin{align} E(X^2)&=\int_{-\infty}^{\infty}x^2f(x)dx=\int_a^bx^2\frac{1}{b-a}dx \quad (x\not\in[a,b]ではf(x)=0) \\ &=\frac{1}{b-a}\left[ \frac{1}{3}x^3 \right]_a^b=\frac{b^3-a^3}{3(b-a)}=\frac{b^2+ab+a^2}{3} \end{align} $$
より
$$ V(X)=E(X^2)-\{E(X)\}^2=\frac{b^2+ab+a^2}{3}-\frac{(a+b)^2}{4}=\frac{(b-a)^2}{12} $$
(2) $$ \begin{align} M_X(t)&=E(e^{tX})=\int_{-\infty}^{\infty}e^{tx}f(x)dx=\int_a^be^{tx}\frac{1}{b-a}dx \quad (x\not\in[a,b]ではf(x)=0) \\ &=\frac{1}{b-a}\left[ \frac{1}{t}e^{tx} \right]_a^b=\frac{e^{bt}-e^{at}}{(b-a)t} \end{align} $$
例1と同じく、ある正の実数 \( x \) に対して小数第一位を四捨五入した数を考えて、もとの実数から四捨五入した数を引いた誤差を \( X \) とする。
このとき、誤差 \( X \) の期待値と標準偏差を求める。
\( X \) は一様分布 \( U(-0.5,0.5) \) に従うので、
$$ E(X)=0 $$
$$ \sigma(X)=\sqrt{V(X)}=\sqrt{\frac{1}{12}}≒0.289 $$
標準一様分布
一様分布において、特に \( a=0,b=1 \) である分布 \( U(0,1) \) のことを標準一様分布といいます。
連続型確率変数 \( X \) が標準一様分布 \( U(0,1) \) に従うとき、確率密度関数 \( f_X(x) \) は次のようになります。
$$ f_X(x)=\begin{cases} 1 & (0≦x≦1) \\ 0 & (その他) \end{cases} $$
標準一様分布の性質は、定理1で \( a=0,b=1 \) としたものが成り立ちます。
確率変数 \( X \) が標準一様分布 \( U(0,1) \) に従っているとする。このとき、
(1) $$ E(X)=\frac{1}{2}, \quad V(X)=\frac{1}{12} $$
(2) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=\frac{e^t-1}{t} $$
指数分布
幾何分布とは、ベルヌーイ試行を初めて成功するまで何回も続けたときに、初めて成功するまでの試行回数が従う確率分布のことでした。
ここでは、それを連続化して、成功する確率 \( p \) が十分小さいベルヌーイ試行を微小時間 \( \Delta t \) ごとに行ったときに、初めて成功するまでにかかる時間 \( X \) が従う確率分布について考えてみましょう。
このとき、初めて成功するまでの回数を \( Y \) とおくと、 \( X=\Delta tY \) となります。(ただし、 \( \Delta t=\frac{x}{n} \))
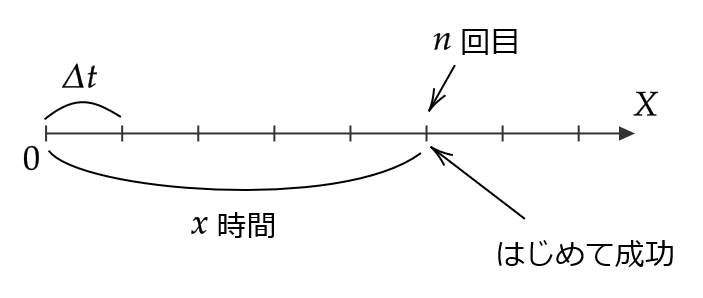
ここで、 \( p=\lambda \Delta t \ (\lambda>0) \) とすると、
$$ \begin{align} P(X≦x)&=P(\frac{x}{n}Y≦x)=P(Y≦n) \\ &=\sum_{k=1}^n(1-p)^{k-1}p \quad (Yは幾何分布に従う) \\ &=\frac{p(1-(1-p)^n)}{1-(1-p)}=1-(1-p)^n=1-(1-\lambda \Delta t)^{\frac{x}{\Delta t}} \\ &≒ 1-e^{-\lambda x} \quad (\Delta tが十分小さいとき) \end{align} $$
したがって、 \( X \) の分布関数が
$$ F(x)=P(X≦x)=\begin{cases} 1-e^{-\lambda x} & (x≧0) \\ 0 & (x<0) \end{cases} $$
となるとき、 \( X \) は指数分布に従うといい、 \( Ex(\lambda) \) と表します。
このとき、 \( X \) の確率密度関数 \( f(x) \) は、次のようになります。
$$ f(x)=\begin{cases} \lambda e^{-\lambda x} & (x≧0) \\ 0 & (x<0) \end{cases} $$
この関数が指数関数であるため、この分布は指数分布とよばれています。
ある地域の役所において、ある課にかかってくる電話の時間間隔を \( X \) (分)とおくと、 \( X \) は指数分布 \( Ex(2) \) に従うことがわかった。
このとき、1回電話がかかってきた後に次に電話がかかってくるまでの時間が1分以下である確率を求める。
1回電話がかかってきた直後の時刻を0とすることにより、求める確率は
$$ \begin{align} P(0<X≦1)&=\int_0^1f(x)dx=\int_0^12e^{-2x}dx \\ &=-[e^{-2x}]^1_0=1-e^{-2}≒0.865 \end{align} $$
指数分布の性質として、次が成り立ちます。
確率変数 \( X \) が指数分布 \( Ex(\lambda) \) に従っているとする。このとき、
(1) $$ E(X)=\frac{1}{\lambda}, \quad V(X)=\frac{1}{\lambda^2} $$
(2) モーメント母関数 \( M_X(t) \) は
$$ M_X(t)=\frac{\lambda}{\lambda-t} $$
(3) (指数分布の無記憶性)
$$ P(X>a+x \ | \ X>a)=P(X>x) \quad (a,x>0) $$
(つまり、時刻 \( x \) で初めて成功する確率と時刻 \( a \) 経過した後にさらに時刻 \( x \) で初めて成功する確率は同じということであり、指数分布は時刻 \( a \) 経過したということを記憶していない)
定理3の証明(気になる方だけクリックしてください)
(1) $$ \begin{align} E(X)&=\int_{-\infty}^{\infty}xf(x)dx=\int_0^{\infty}x\lambda e^{-\lambda x}dx \quad (x\not\in[0,\infty)ではf(x)=0) \\ &=\left[ -xe^{-\lambda x} \right]_0^{\infty}+\int_0^{\infty}e^{-\lambda x}dx=\left[ -\frac{1}{\lambda}e^{-\lambda x} \right]^{\infty}_0=\frac{1}{\lambda} \end{align} $$
また、
$$ \begin{align} E(X^2)&=\int_{-\infty}^{\infty}x^2f(x)dx=\int_0^{\infty}x^2\lambda e^{-\lambda x}dx \quad (x\not\in[0,\infty)ではf(x)=0) \\ &=\left[ -x^2e^{-\lambda x} \right]_0^{\infty}+\int_0^{\infty}2xe^{-\lambda x}dx=\frac{2}{\lambda^2} \end{align} $$
より
$$ V(X)=E(X^2)-\{E(X)\}^2=\frac{2}{\lambda^2}-\frac{1}{\lambda^2}=\frac{1}{\lambda^2} $$
(2) $$ \begin{align} M_X(t)&=E(e^{tX})=\int_{-\infty}^{\infty}e^{tx}f(x)dx=\int_0^{\infty}e^{tx}\lambda e^{-\lambda x}dx \quad (x\not\in[0,\infty)ではf(x)=0) \\ &=\lambda \left[ -\frac{1}{\lambda-t}e^{-(\lambda-t)x} \right]^{\infty}_0=\frac{\lambda}{\lambda-t} \end{align} $$
(3) 条件付き確率の定義より、
$$ \begin{align} P(X>a+x \ | \ X>a)&=\frac{P(X>a+x, X>a)}{P(X>a)} \\ &=\frac{P(X>a+x)}{P(X>a)} \quad (X>a+xであればX>aなのは当然) \\ &=\frac{1-P(X≦a+x)}{1-P(X≦a)} \\ &=\frac{e^{-\lambda(a+x)}}{e^{-\lambda a}}=e^{-\lambda x}=P(X>x) \end{align} $$
ある地域の役所において、ある課にかかってくる電話の時間間隔を \( X \) (分)とおくと、 \( X \) は指数分布 \( Ex(2) \) に従うことがわかった。
このとき、1回電話がかかってきた後に次に電話がかかってくるまでの時間の平均と標準偏差を求める。
$$ E(X)=\frac{1}{2}=0.5 $$
$$ \sigma(X)=\sqrt{V(X)}=\sqrt{\frac{1}{4}}=\frac{1}{2}=0.5 $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

