こんにちは、ひかりです。
今回は線形代数学から行列式の定義について解説していきます。
前回解説した複素行列について知りたい方は下のリンクからご覧ください。
この記事では以下のことを紹介します。
- 行列式とは何か?
- 1~3次の正方行列に関する行列式の定義について
- 余因子について
- 4次以上の正方行列も含めた行列式の定義について
行列式を考える意味
はじめに、これから解説していく行列式というものがなぜ必要になってくるのかをすこしだけお話しします。
線形代数学05の記事にて正則行列と逆行列について解説しました。見ていない方は以下のリンクからご覧ください。
その記事では例として簡単な正方行列に対して、その行列が正則かどうか、また正則ならば逆行列を求めました。
ただし、行列がいつも簡単なものばかりとは限りません。
なかには正則かどうかを判定するのや逆行列を求めるのが難しい行列も存在します。
そのため、正則判定や逆行列の求め方の公式のようなものがあると便利です。
その公式に深く関わっているのがこれから解説していく行列式というものになります。
1~3次の正方行列に関する行列式の定義
まず、1~3次の正方行列に関する行列式を定義します。
1次正方行列 \( A=(a) \) に対して、 \( A \) の行列式を \( |A| \) または \( |a| \) とかき、次で定める。
$$ |A|=|a|=a $$
(1) \( A=(2) \) の行列式 \( |A| \) は \( |A|=2 \)
(2) \( A=(-3) \) の行列式 \( |A| \) は \( |A|=-3 \) ( \( 3 \) ではない。)
2次正方行列 \( A=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \) に対して、 \( A \) の行列式を \( |A| \) または \( \begin{vmatrix} a & b \\ c & d \end{vmatrix} \) とかき、次で定める。
$$ |A|=\begin{vmatrix} a & b \\ c & d \end{vmatrix}=ad-bc $$
この \( ad-bc \) という値に見覚えがあると思います。
線形代数学05の記事の最後に書いた2次正方行列の逆行列の公式に出てきました。
少しずつ逆行列と行列式の関係が見えてきましたでしょうか。
(1) \( A=\begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} \) のとき、
$$ |A|=\begin{vmatrix} 1 & 2 \\ 2 & 1 \end{vmatrix}=1\times 1-2\times 2=-3 $$
(2) \( A=\begin{pmatrix} 1 & 2 \\ 2 & 4 \end{pmatrix} \) のとき、
$$ |A|=\begin{vmatrix} 1 & 2 \\ 2 & 4 \end{vmatrix}=1\times 4-2\times 2=0 $$
3次正方行列 \( A=\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} \) に対して、 \( A \) の行列式を \( |A| \) または \( \begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \) とかき、次で定める。
$$ \begin{align} |A|&=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix} \\ &=a_{11}a_{22}a_{33}+a_{13}a_{32}a_{21}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{11}a_{23}a_{32}-a_{12}a_{21}a_{33} \end{align} $$
この定義だけ見るととても複雑に見えるが、次のような覚え方があります。(サラスの公式)
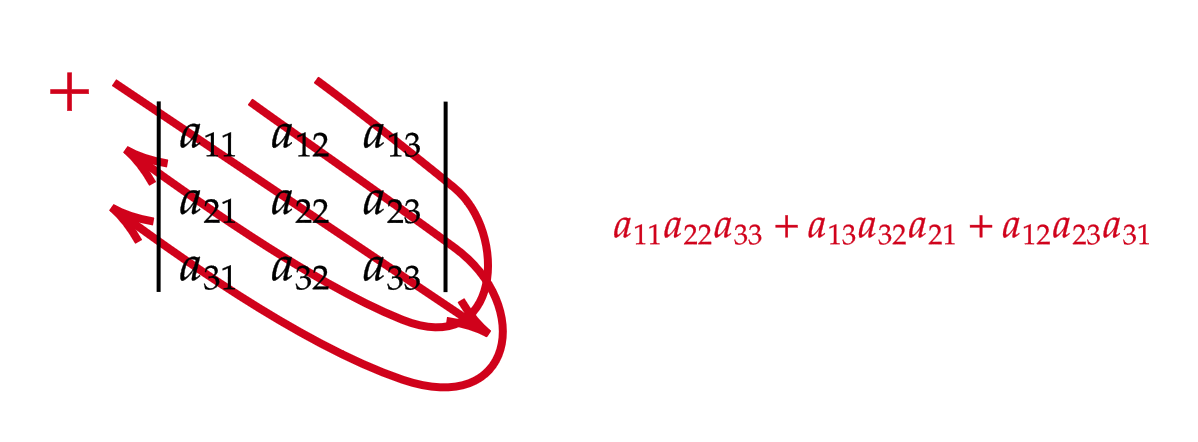
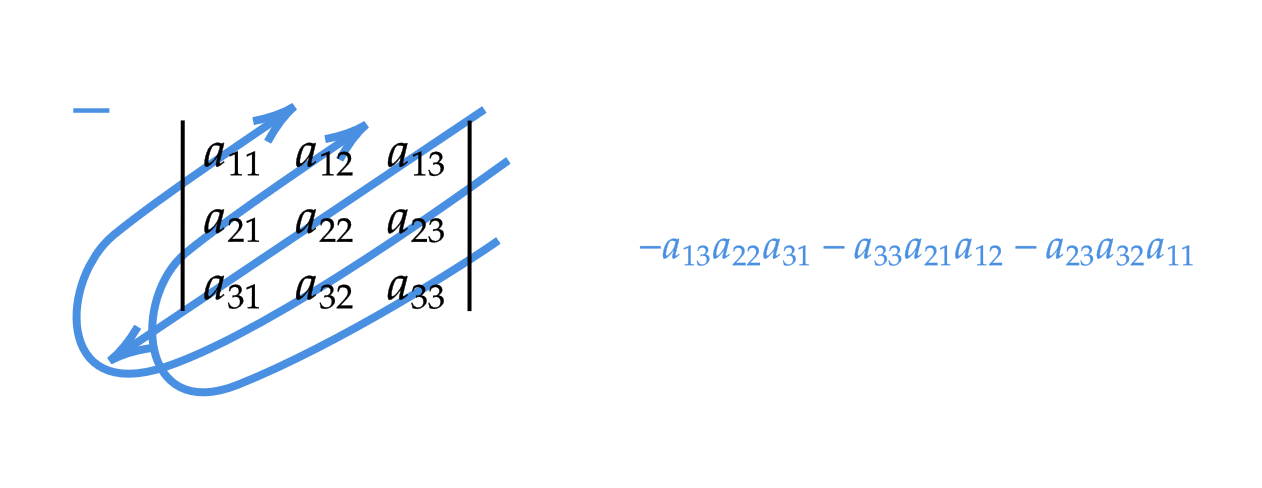
\( A=\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \) のとき、
$$ \begin{align} |A|&=\begin{vmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{vmatrix} \\ &=1\times 5\times 9+2\times 6\times 7+3\times 4\times 8-3\times 5\times 7-2\times 4\times 9-1\times 6\times 8=0 \end{align} $$
余因子の定義
このあと、4次以上の正方行列に関する行列式の定義をしていきたい。
そのために必要な余因子というものを定義します。
かなり複雑なので、定義と例と見比べながらご覧ください。
正方行列 \( A=\begin{pmatrix} a_{11} & \dots & a_{1j} & \dots & a_{1n} \\ \vdots & & \vdots & & \vdots \\ a_{i1} & \dots & a_{ij} & \dots & a_{in} \\ \vdots & & \vdots & & \vdots \\ a_{n1} & \dots & a_{nj} & \dots & a_{nn} \end{pmatrix} \) に対して、第 \( i \) 行と第 \( j \) 列を取り除いた行列を
$$ \widetilde{A}_{ij}=\begin{pmatrix} a_{11} & \dots & a_{1(j-1)} & a_{1(j+1)} & \dots & a_{1n} \\ \vdots & & \vdots & \vdots & & \vdots \\ a_{(i-1)1} & \dots & a_{(i-1)(j-1)} & a_{(i-1)(j+1)} & \dots & a_{(i-1)n} \\ a_{(i+1)1} & \dots & a_{(i+1)(j-1)} & a_{(i+1)(j+1)} & \dots & a_{(i+1)n} \\ \vdots & & \vdots & \vdots & & \vdots \\ a_{n1} & \dots & a_{n(j-1)} & a_{n(j+1)} & \dots & a_{nn} \end{pmatrix} $$
と表す。このとき、 \( \widetilde{a}_{ij}=(-1)^{i+j}|\widetilde{A}_{ij}| \) とおき、 \( a_{ij} \) の余因子または \( A \) の \( (i,j) \) 余因子という。
(1) \( A=\begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} \) のとき、 \( \widetilde{A}_{22}=(1) \) ( \( A \) で第2行と第2列を取り除く) なので、
$$ \widetilde{a}_{22}=(-1)^{2+2}|\widetilde{A}_{22}|=1 $$
(2) \( A=\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix} \) のとき、 \( \widetilde{A}_{12}=\begin{pmatrix} 4 & 6 \\ 7 & 9 \end{pmatrix} \) ( \( A \) で第1行と第2列を取り除く) なので、
$$ \widetilde{a}_{12}=(-1)^{1+2}|\widetilde{A}_{12}|=-(36-42)=6 $$
4次以上の正方行列も含めた行列式の定義
いよいよ4次以上の正方行列も含めた行列式の定義を述べていきます。
これから述べる定義は行列式の帰納的定義とよばれるものとなります。
\( n \) 次正方行列 \( A \) に対して、 \( A \) の行列式 \( |A| \) を帰納的に定義する。
(i) \( n=1 \) に対しては、すでに定めた。
(ii) \( n \) 次正方行列 \( A \) に対して、 \( A \) の行列式 \( |A| \) を
$$ |A|=a_{1j}\widetilde{a}_{1j}+a_{2j}\widetilde{a}_{2j}+\dots +a_{nj}\widetilde{a}_{nj} \quad (j=1,2,\dots,n \ \text{のどれでも}) $$
で定める。(これを第 \( j \) 列による(余因子)展開という。)
これを用いて、4次の正方行列の行列式を求めてみましょう。
\( A=\begin{pmatrix} 1 & 2 & 0 & 1 \\ 0 & 0 & 2 & 2 \\ 0 & 1 & 1 & 2 \\ 2 & 1 & 1 & 2 \end{pmatrix} \) のとき、 第 \( 1 \) 列による展開で行列式 \( |A| \) を求めると、
$$ \begin{align} |A|&=a_{11}\widetilde{a}_{11}+a_{21}\widetilde{a}_{21}+a_{31}\widetilde{a}_{31}+a_{41}\widetilde{a}_{41} \\ &=1\times (-1)^{1+1}|\widetilde{A}_{11}|+0\times \widetilde{a}_{21}+0\times \widetilde{a}_{31}+2\times (-1)^{4+1}|\widetilde{A}_{41}| \\ &=\begin{vmatrix} 0 & 2 & 2 \\ 1 & 1 & 2 \\ 1 & 1 & 2 \end{vmatrix}-2\begin{vmatrix} 2 & 0 & 1 \\ 0 & 2 & 2 \\ 1 & 1 & 2 \end{vmatrix} \\ &=(0+4+2-2-0-4)-2(8+0+0-2-4-0) \\ &=-4 \end{align} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

