こんにちは、ひかりです。
今回は確率・統計から事象と確率について解説していきます。
この記事では以下のことを紹介します。
- 試行・事象と確率の古典的定義・性質について
- 確率の統計的定義と公理的定義について
- 確率の加法定理と余事象について
試行・事象と確率の古典的定義・性質
試行と事象
さいころ投げのように実際に行ってみないと結果が予測できないような実験や観察のことを試行といいます。
また、試行の結果として起きることがらのことを事象といいます。
試行によって起こりうる結果の全体の集合を標本空間といい、 \( \Omega \) で表します。
(1) さいころを投げて何の目が出るかを考える。このとき、
試行:さいころを1回投げて何の目が出るかを見る
事象:1の目が出る、偶数の目が出るなど
標本空間:1の目が出ることを単に \( 1 \) と表せば、
$$ \Omega=\{ 1,2,3,4,5,6 \} $$
(2) 今度は、さいころを投げるが出た目が偶数か奇数かのみに注目することを考える。このとき、
試行:さいころを1回投げて出た目が偶数か奇数を見る
事象:偶数の目が出る、奇数の目が出る
標本空間:奇数の目が出ることを \( O \) 、偶数の目が出ることを \( E \) と表せば、
$$ \Omega=\{ O,E \} $$
このように同じさいころ投げでも何に注目するかによって、標本空間は変わる。
この標本空間 \( \Omega \) に対して、各事象というのは \( \Omega \) の部分集合で表されます。
その各事象を表すのに \( A,B, \cdots \) などの文字を用います。
とくに、 \( \Omega \) 全体となる事象(つまり、必ず起きる事象)のことを全事象といい、 \( \Omega \) の1個の要素だけからなる部分集合で表される事象を根元事象といいます。
逆に、決して起こらない事象を空事象といい、 \( \emptyset \) と表します。
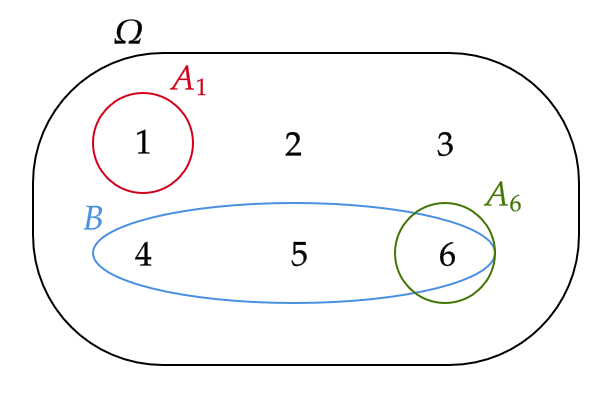
(1) 例1の(1)を考える。このとき、
全事象:1か2か3か4か5か6の目が出る事象 \( \{1,2,3,4,5,6 \} \) (つまり、必ず起きる事象である)
根元事象:1の目が出る事象 \( A_1=\{ 1 \} \) 、 \( \cdots \) 、6の目が出る事象 \( A_6=\{ 6 \} \)
他の事象:奇数の目が出る事象 \( B=\{ 1,3,5 \} \) 、偶数の目が出る事象 \( C=\{ 2,4,6 \} \) など
これらを図で考えると次のようになる。
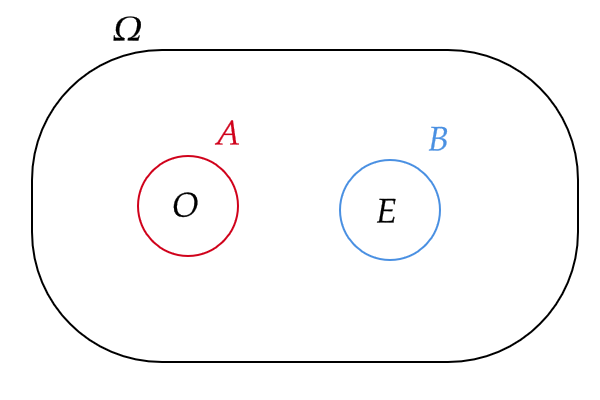
(2) 例1の(2)を考える。このとき、
全事象:偶数か奇数の目が出る事象 \( \{ O,E \} \) (つまり、必ず起きる事象である)
根元事象:奇数の目が出る事象 \( A=\{ O \} \) 、偶数の目が出る事象 \( B=\{ E \} \)
これらを図で考えると次のようになる。
確率の古典的定義
ここでは、中学・高校から馴染みのある確率の古典的定義を与えます。
まず、ある試行において、起こりうるすべての結果がどれも同じ程度に起こると期待できるとき、その試行の1つの結果からなる根元事象は同様に確からしいといいます。
(1) さいころを1回投げて何の目が出るかを見る試行における根元事象は
$$ \{ 1 \}, \ \{2 \}, \ \{3 \}, \ \{4 \}, \ \{5\}, \ \{6 \} $$
の6つであり、これらは同様に確からしい。
(2) コインを1回投げて表か裏かを見る試行における根元事象は
$$ \{ H \}, \ \{T \} \quad (Hは表が出る、Tは裏が出る事象)$$
の2つであり、これらは同様に確からしい。
それでは、確率の古典的定義を与えます。
全事象 \( \Omega \) のすべての根元事象が同様に確からしいとする。
全事象 \( \Omega \) の根元事象の個数を \( n(\Omega) \) 、考える事象 \( A \) の根元事象の個数を \( n(A) \) とするとき、事象 \( A \) の確率 \( P(A) \) を次で定める。
$$ P(A)=\frac{n(A)}{n(\Omega)} $$
それでは、高校数学で学んできた確率の計算をしてみましょう。
(1) 1個のさいころを投げるとき、偶数の目が出る事象 \( A \) の確率は、\( A=\{ 2,4,6 \} \) より、
$$ P(A)=\frac{n(A)}{n(\Omega)}=\frac{3}{6}=\frac{1}{2} $$
(2) 2個のさいころを投げるとき、目の和が \( 6 \) となる事象 \( A \) の確率を求める。
2個のさいころを投げるときの目の出方は \( 36 \) 通りである。
このとき、目の和が \( 6 \) となるのは
$$ (1,5), \ (2,4), \ (3,3), \ (4,2), \ (5,1) $$
の5通りである。したがって、
$$ P(A)=\frac{n(A)}{n(\Omega)}=\frac{5}{36} $$
(3) 10本のくじの中に当たりくじが4本入っている。この中から同時に2本のくじを引くとき、2本とも当たりくじである事象 \( A \) の確率を求める。
10本のくじから同時に2本のくじを引くとき、その引き方は全部で \( {}_{10}C_2 \) 通りある。
(ここで、 \( {}_nC_r=\frac{n!}{r!(n-r)!} \) である。)
このとき、2本とも当たりくじとなる引き方は \( {}_4C_2 \) 通りである。したがって、
$$ P(A)=\frac{n(A)}{n(\Omega)}=\frac{{}_4C_2}{{}_{10}C_2}=\frac{\frac{4\cdot 3}{2\cdot 1}}{\frac{10\cdot 9}{2\cdot 1}}=\frac{6}{45}=\frac{2}{15} $$
(4) 5人が1列に並ぶとき、特定の2人が隣り合う事象 \( A \) の確率を求める。
5人が1列に並ぶ並び方は \( {}_5P_5 \) 通りである。
(ここで、 \( {}_nP_r=\frac{n!}{(n-r)!} \) である。)
このとき、特定の2人が隣り合う並び方は \( {}_4P_4\times 2! \) 通りである。
(特定の2人を1つにまとめて4人が1列に並ぶ並び方を考えればよい。そして、1つにまとめた枠に2人が並ぶ並び方は \( 2! \) 通りなので、 \( {}_4P_4\times 2! \) 通りである。)
したがって、
$$ P(A)=\frac{n(A)}{n(\Omega)}=\frac{{}_4P_4\times 2!}{{}_5P_5}=\frac{4\cdot 3 \cdot 2 \cdot 1 \times 2}{5\cdot 4\cdot 3 \cdot 2 \cdot 1}=\frac{2}{5} $$
確率の基本的性質
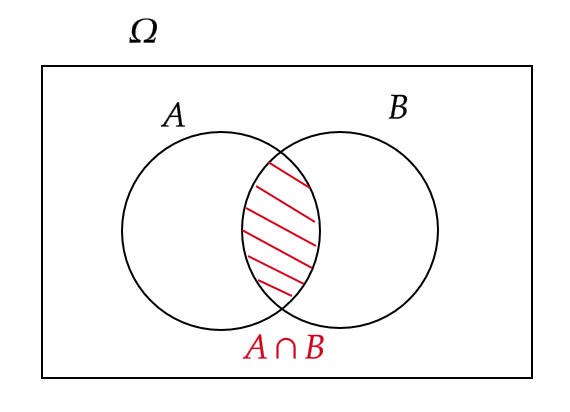
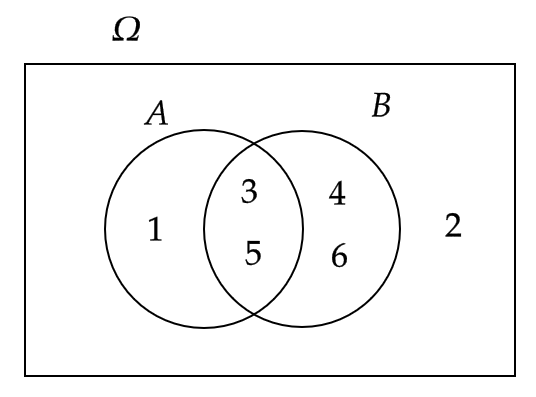
2つの事象 \( A,B \) に対して、 \( A \) と \( B \) がともに起こる事象を \( A \) と \( B \) の積事象といい、 \( A\cap B \) と表します。
(この図のことをベン図といいます。)
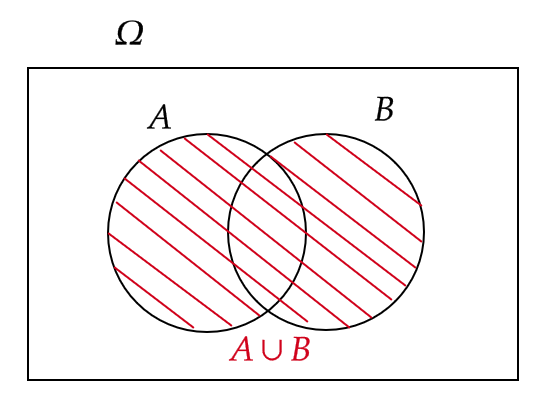
また、 \( A \) もしくは \( B \) が起こる事象を \( A \) と \( B \) の和事象といい、 \( A\cup B \) と表します。
1個のさいころを投げるとき、奇数の目が出る事象を \( A \) 、3以上の目が出る事象を \( B \) とすると、積事象 \( A\cap B \) 、和事象 \( A\cup B \) を求める。
$$ A\cap B=\{ 3,5 \}, \quad A\cup B=\{1,3,4,5,6 \} $$
ベン図で表すと次のようになる。
2つの事象 \( A,B \) が同時に起こることがないとき、 \( A \) と \( B \) は互いに排反である、もしくは排反事象といいます。
このとき、 \( A\cap B=\emptyset \) となります。
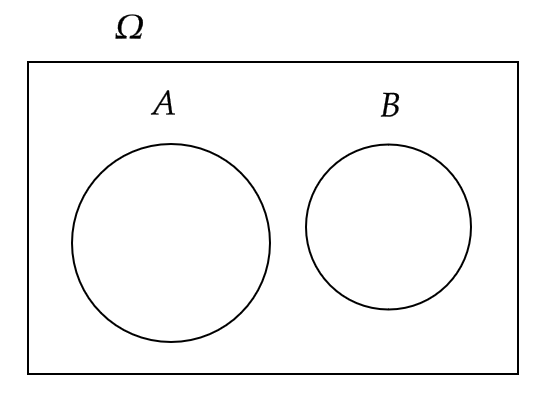
したがって、次が成り立ちます。
$$ P(A\cap B)=\frac{n(A\cap B)}{n(\Omega)}=0 $$
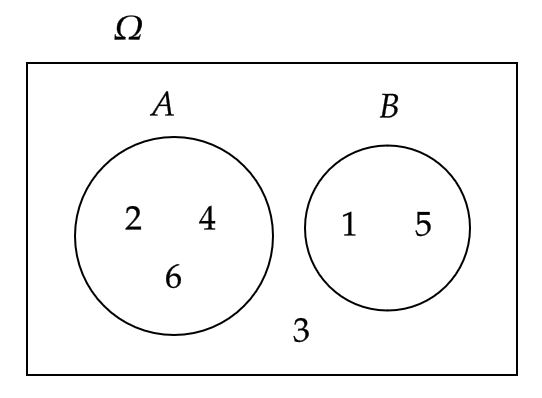
1個のさいころを投げるとき、偶数の目が出る事象を \( A \) 、1または5の目が出る事象を \( B \) とすると、 \( A \) と \( B \) は同時には起こらない。つまり、
$$ A\cap B=\{ 2,4,6 \} \cap \{ 1,5 \} =\emptyset $$
よって、 \( A \) と \( B \) は互いに排反である。
ベン図で表すと次のようになる。
これらを踏まえると、確率の性質として次が成り立ちます。
すべての根元事象が同様に確からしいとする。
このとき、確率 \( P(A) \) は次の4つの性質をみたす。
(1) 任意の事象 \( A \) に対して、 \( 0≦P(A)≦1 \)
(2) \( P(\Omega)=1 \)
(3) \( P(\emptyset)=0 \)
(4) \( A,B \) が互いに排反であるとき、
$$ P(A\cup B)=P(A)+P(B) $$
定理1の証明(気になる方だけクリックしてください)
(1) 任意の事象 \( A \) は \( \Omega \) の部分集合で表されているため、
$$ 0≦n(A)≦n(\Omega) $$
が成り立ちます。よって、各辺 \( n(\Omega) \) で割ると、
$$ 0≦\frac{n(A)}{n(\Omega)}≦1 \quad つまり \quad 0≦P(A)≦1 $$
(2) $$ P(\Omega)=\frac{n(\Omega)}{n(\Omega)}=1 $$
(3) 空事象 \( \emptyset \) は根元事象を1つも含まない事象であるので、 \( n(\emptyset)=0 \)
よって、
$$ P(\emptyset)=\frac{n(\emptyset)}{n(\Omega)}=0 $$
(4) 事象 \( A,B \) が互いに排反であるとき、 \( A\cap B=\emptyset \) であるので、和事象 \( A\cup B \) に含まれる根元事象の数は
$$ n(A\cup B)=n(A)+n(B) $$
となります。したがって、
$$ P(A\cup B)=\frac{n(A\cup B)}{n(\Omega)}=\frac{n(A)+n(B)}{n(\Omega)}=\frac{n(A)}{n(\Omega)}+\frac{n(B)}{n(\Omega)}=P(A)+P(B) $$
確率の統計的定義と公理的定義
確率の統計的定義
確率の別の定義である統計的定義を与えます。
同じ条件で試行を \( N \) 回繰り返し行って事象 \( A \) が起こった回数を \( N(A) \) とする。
このとき、 \( \frac{N(A)}{N} \) を \( N \) 回の試行に対する事象 \( A \) の起こる相対頻度という。
もし、 \( N \) が大きくなるにつれて相対頻度が定数に収束するとき、つまり、
$$ P(A)=\lim_{n\to\infty}\frac{N(A)}{N} $$
が存在するとき、 \( P(A) \) を事象 \( A \) が起こる確率という。
さいころを1回投げて1の目が出る事象 \( A \) の確率を統計的定義によって求める。
さいころを \( N \) 回投げて1が出た回数 \( N(A) \) を数えていく。
そして、相対頻度 \( \frac{N(A)}{N} \) を各 \( N \) で求めていき、 \( N \to \infty \) とする。すると、
$$ P(A)=\lim_{n\to\infty}\frac{N(A)}{N}=\frac{1}{6} $$
となることが予想される。
ただし、さいころを無限回投げるというのは現実では不可能なので、この定義は現実的ではない。
確率の公理的定義
確率の古典的定義では、すべての根元事象が同様に確からしいときではないと確率が定義できないです。
さらに、根元事象の数が有限ではなく無限の場合にも確率を求めることができません。
また、確率の統計的定義では、同様に確からしい必要はないが、試行を無限回繰り返す必要があるので現実的ではないです。
よって、確率の別の定義を考える必要が出てきます。
そこで、確率を定義してからその性質(定理1)を見るのではなく、確率に必要とされる性質そのものを定義とすることにより、問題を解決していきます。
定理1を改良して、次のように確率を公理的に定義します。
次の3つの性質をみたす関数 \( P \) のことを確率という。
(1) 任意の事象 \( A \) に対して、 \( 0≦P(A)≦1 \)
(2) \( P(\Omega)=1 \)
(3) \( A_1,A_2,\cdots \) が互いに排反(つまりどの2つの事象 \( A_i,A_j \) をみても互いに排反)であるとき、
$$ P(A_1\cup A_2\cup \cdots )=P(A_1)+P(A_2)+\cdots $$
ちなみに、 \( P(\emptyset)=0 \) は定義3に含めなくても定義3の3つの性質より示すことができます。
$$ P(\emptyset)=0 $$
定理2の証明(気になる方だけクリックしてください)
事象 \( \Omega \) を次のように表します。
$$ \Omega=\Omega\cup \emptyset \cup \emptyset \cup \cdots $$
すると、 \( \Omega \) と \( \emptyset \) は互いに排反であるので、定義3(3)より、
$$ P(\Omega)=P(\Omega\cup \emptyset \cup \emptyset \cup \cdots)=P(\Omega)+P(\emptyset)+P(\emptyset)+\cdots $$
となります。
定義3(2)より、 \( P(\Omega)=1<\infty \) であるので、最両辺 \( P(\Omega) \) を引くと、
$$ 0=P(\emptyset)+P(\emptyset)+\cdots $$
したがって、
$$ P(\emptyset)=0 $$
これ以降、確率といったら定義3の公理的定義として話を進めます。
(ただし、同様に確からしい状況であれば古典的定義の方が計算はしやすいので、具体的な計算に関しては状況に応じて使い分けます。)
確率の加法定理と余事象
確率の加法定理
それでは、さらなる確率の性質を見ていきましょう。
まず、定理1の(4)で示した性質を確率の加法定理といいます。つまり、
事象 \( A,B \) が互いに排反であるとき、
$$ P(A\cup B)=P(A)+P(B) $$
これを公理的定義のもと示していきましょう。
定理3の証明(気になる方だけクリックしてください)
事象 \( A\cup B \) を次のように表します。
$$ A\cup B=A\cup B \cup \emptyset \cup \emptyset \cup \cdots $$
すると、 \( A \) と \( B \) は仮定より互いに排反であるので、定義3(3)を用いると、
$$ P(A\cup B)=P(A \cup B \cup \emptyset \cup \emptyset \cup \cdots)=P(A)+P(B)+P(\emptyset)+P(\emptyset)+\cdots $$
よって、定理2より、 \( P(\emptyset)=0 \) であるので、
$$ P(A\cup B)=P(A)+P(B) $$
赤球4個と白球6個が入っている袋から、同時に2個の球を取り出すとき、それらが同じ色である確率を求める。
赤球を2個取り出す事象を \( A \) 、白球を2個取り出す事象を \( B \) とする。
このとき、2個とも同じ色である事象は \( A\cup B \) で表される。
まず、事象 \( A,B \) の確率は
$$ P(A)=\frac{n(A)}{n(\Omega)}=\frac{{}_4C_2}{{}_{10}C_2}=\frac{6}{45}, \quad P(B)=\frac{n(B)}{n(\Omega)}=\frac{{}_6C_2}{{}_{10}C_2}=\frac{15}{45} $$
\( A \) と \( B \) は互いに排反なので、定理3より、
$$ P(A\cup B)=P(A)+P(B)=\frac{6}{45}+\frac{15}{45}=\frac{21}{45}=\frac{7}{15} $$
余事象
事象 \( A \) に対して、 \( A \) が起こらないという事象を \( A \) の余事象といい、 \( A^c \) もしくは \( \overline{A} \) で表します。
また、事象 \( A^c \) も余事象 \( (A^c)^c \) は \( A \) が起こる事象となるので、
$$ (A^c)^c=A $$
となります。
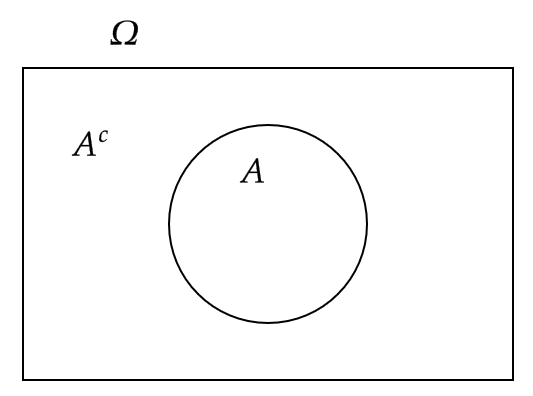
さいころを1回投げるとき、偶数の目が出る事象を \( A \) とおくと、余事象 \( A^c \) は偶数の目が出ない事象、つまり、奇数の目が出る事象である。
ベン図で表すと次のようになる。
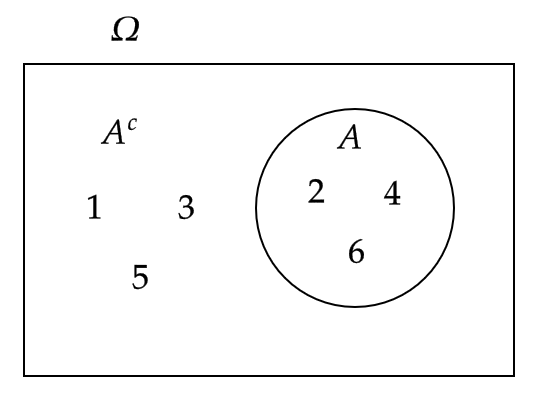
余事象 \( A^c \) の確率は次のように求められます。
$$ P(A^c)=1-P(A) $$
定理4の証明(気になる方だけクリックしてください)
$$ A\cup A^c=\Omega $$
かつ、 \( A \) と \( A^c \) は互いに排反であるので、定理3より、
$$ 1=P(\Omega)=P(A\cup A^c)=P(A)+P(A^c) $$
したがって、
$$ P(A^c)=1-P(A) $$
20本のくじの中に当たりくじが5本ある。この中から同時に3本のくじを引くとき、少なくとも1本が当たりくじである確率を求める。
少なくとも1本が当たりくじであるという事象は、3本ともくじがはずれであるという事象 \( A \) の余事象 \( A^c \) である。
よって、
$$ P(A)=\frac{n(A)}{n(\Omega)}=\frac{{}_{15}C_3}{{}_{20}C_3}=\frac{91}{228} $$
であるので、
$$ P(A^c)=1-P(A)=1-\frac{91}{228}=\frac{137}{228} $$
確率の加法定理の一般化
では、事象 \( A,B \) が互いに排反でない場合の \( A\cup B \) の確率はどうなるのでしょうか。
任意の事象 \( A,B \) に対して、
$$ P(A\cup B)=P(A)+P(B)-P(A\cap B) $$
定理5の証明(気になる方だけクリックしてください)
\( A,B,A\cup B \) をそれぞれ次のように分解します。
$$ A=A\cap \Omega=A\cap (B\cup B^c)=(A\cap B)\cup (A\cap B^c) $$
$$ B=\Omega\cap B=(A\cup A^c)\cap B=(A\cap B)\cup (A^c\cap B) $$
$$ A\cup B=(A\cap B^c)\cup (A^c\cap B)\cup (A\cap B) $$
分解した要素はすべて互いに排反なので定理3より、
$$ P(A)=P(A\cap B)+P(A\cap B^c) $$
$$ P(B)=P(A\cap B)+P(A^c\cap B) $$
$$ P(A\cup B)=P(A\cap B^c)+P(A^c\cap B)+P(A\cap B) $$
したがって、
$$ \begin{align} P(A\cup B)&=P(A\cap B^c)+P(A^c\cap B)+P(A\cap B) \\ &=\{ P(A)-P(A\cap B) \}+\{ P(B)-P(A\cap B) \}+P(A\cap B) \\ &=P(A)+P(B)-P(A\cap B) \end{align} $$
1から100までの数を1つずつ書いた100枚のカードの中から1枚のカードを取り出す。
このとき、カードの数が2の倍数または3の倍数である確率を求める。
取り出したカードの数が2の倍数である事象を \( A \) 、3の倍数である事象を \( B \) とすると、求める確率は \( P(A\cup B ) \) である。ここで、
$$ A=\{ 2\cdot 1, \ 2\cdot 2, \ \cdots, \ 2\cdot 50 \} $$
$$ B=\{ 3\cdot 1, \ 3\cdot 2, \ \cdots, \ 3\cdot 33 \} $$
$$ A\cap B=\{ 6\cdot 1, \ 6\cdot 2, \ \cdots, \ 6\cdot 16 \} $$
であるので、
$$ P(A)=\frac{n(A)}{n(\Omega)}=\frac{50}{100}, \ P(B)=\frac{n(B)}{n(\Omega)}=\frac{33}{100}, $$
$$ P(A\cap B)=\frac{n(A\cap B)}{n(\Omega)}=\frac{16}{100} $$
したがって、
$$ \begin{align} P(A\cup B)&=P(A)+P(B)-P(A\cap B) \\ &=\frac{50}{100}+\frac{33}{100}-\frac{16}{100}=\frac{67}{100} \end{align} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

