こんにちは、ひかりです。
今回は確率・統計から時系列データの記述と分析について解説していきます。
この記事では以下のことを紹介します。
- 時系列データについて
- 時系列データの指数化と変化率・伸び率について
- 時系列データの変動分解について
- 時系列データの自己相関について
時系列データ
いままで扱ってきたデータ \( x_1,x_2,\cdots, x_n \) は同じ時期(時間)で得られたデータとなります。
今回扱うのはデータ \( x_1,x_2,\cdots,x_n \) が時間の順に得られているものであり、これを時系列データといいます。
時系列データは時間を横軸にした折れ線グラフで表現することができます。
ある都市の20年間の人口のデータを考えます。これを折れ線グラフで表現すると次のようになります。
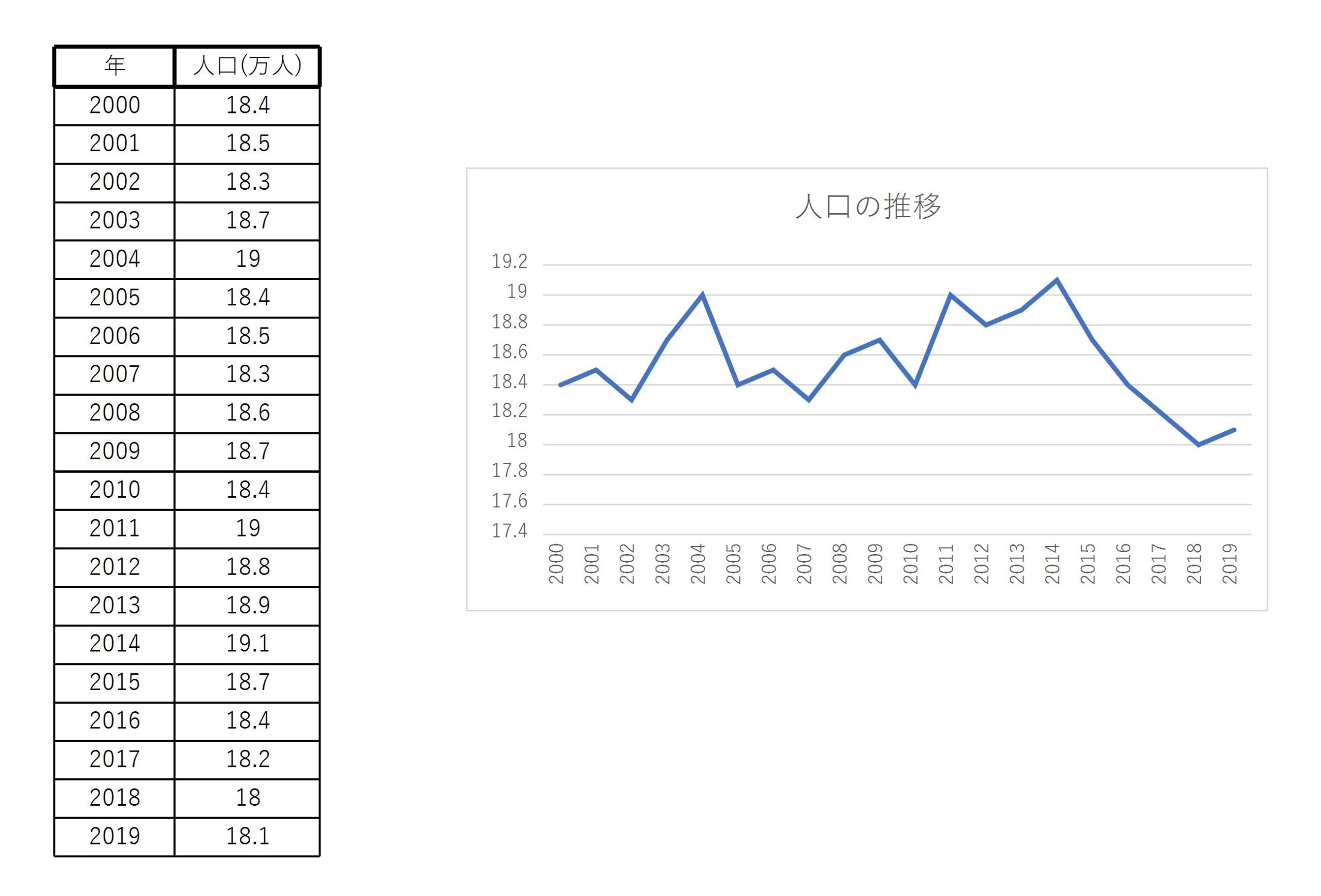
時系列データの指数化と変化率・伸び率
では、この時系列データを分析することを考えましょう。
時系列データの場合、複数の時系列データを比較しながら分析することが多いです。
そのときに、用いられる指標を紹介していきます。
時系列データの指数化
まず、時系列データの指数化について紹介します。
各時点でのデータ \( x_0,x_1,\cdots,x_{T-1},x_T \) に対して、基準となる時点 \( s \) のデータを \( x_s \) とするとき、各時点 \( t \) の指数 \( q_t \) を次で定める。
$$ q_t=\frac{x_t}{x_s}, \quad (t=0,1,2,\cdots,T) $$
これによって、データ \( x_0,x_1,\cdots,x_T \) を \( q_0,q_1,\cdots,q_T \) に変換することを時系列データの時点 \( s \) を基準とする指数化という。
これにより、複数の時系列データを同じ値にそろえることができます。
指数化した時系列データも時間を横軸にした折れ線グラフで表現することができます。
3つの都市の20年間の人口のデータを考えます。これを普通に折れ線グラフで表現すると次のようになります。
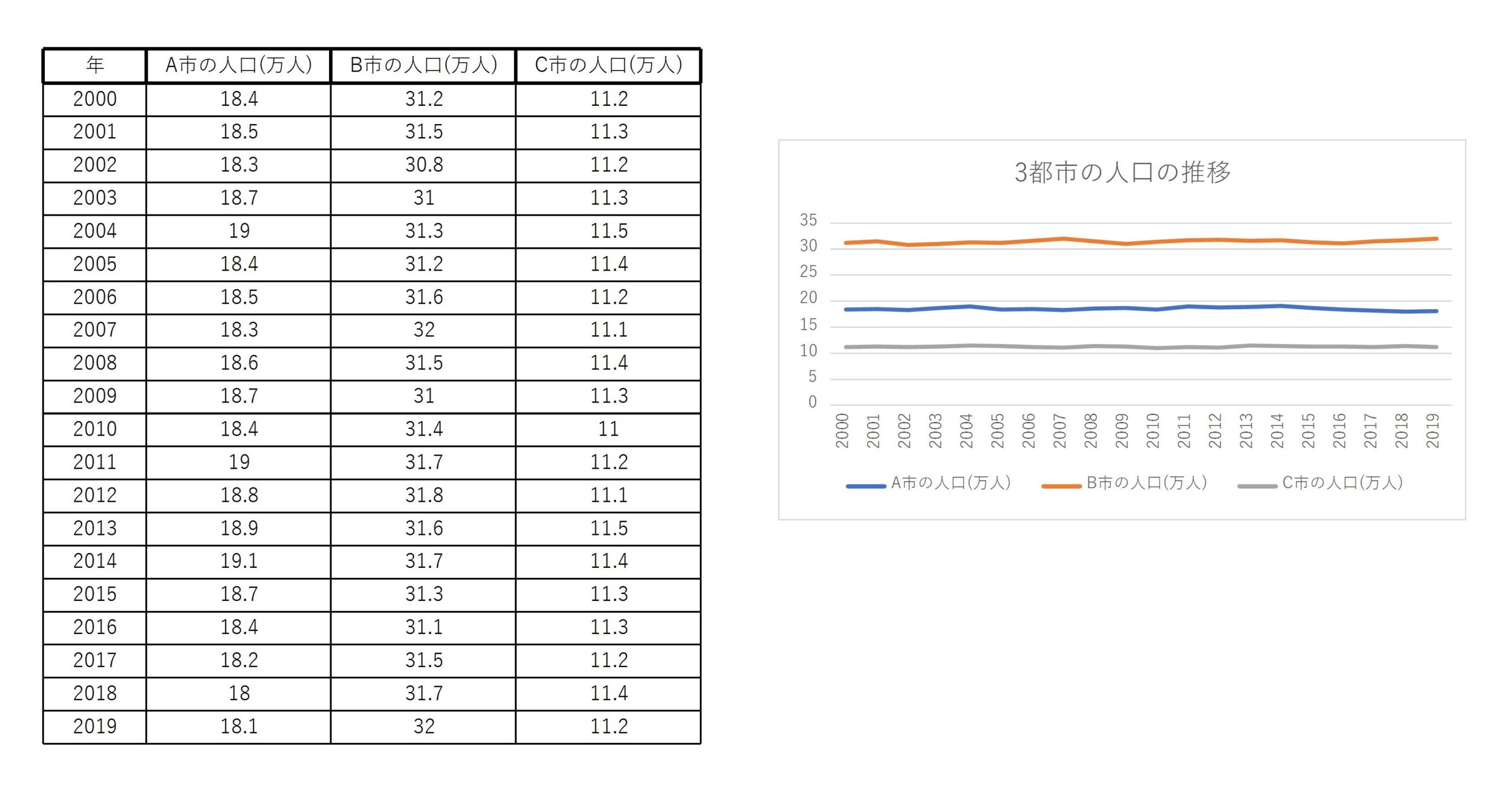
これでは各都市の人口の変化がわかりにくいです。
よって、各都市を \( 2000 \) 年を基準とする指数化を行います。(小数点以下第4位を四捨五入)
そして指数化した時系列データを折れ線グラフで表現すると次のようになります。
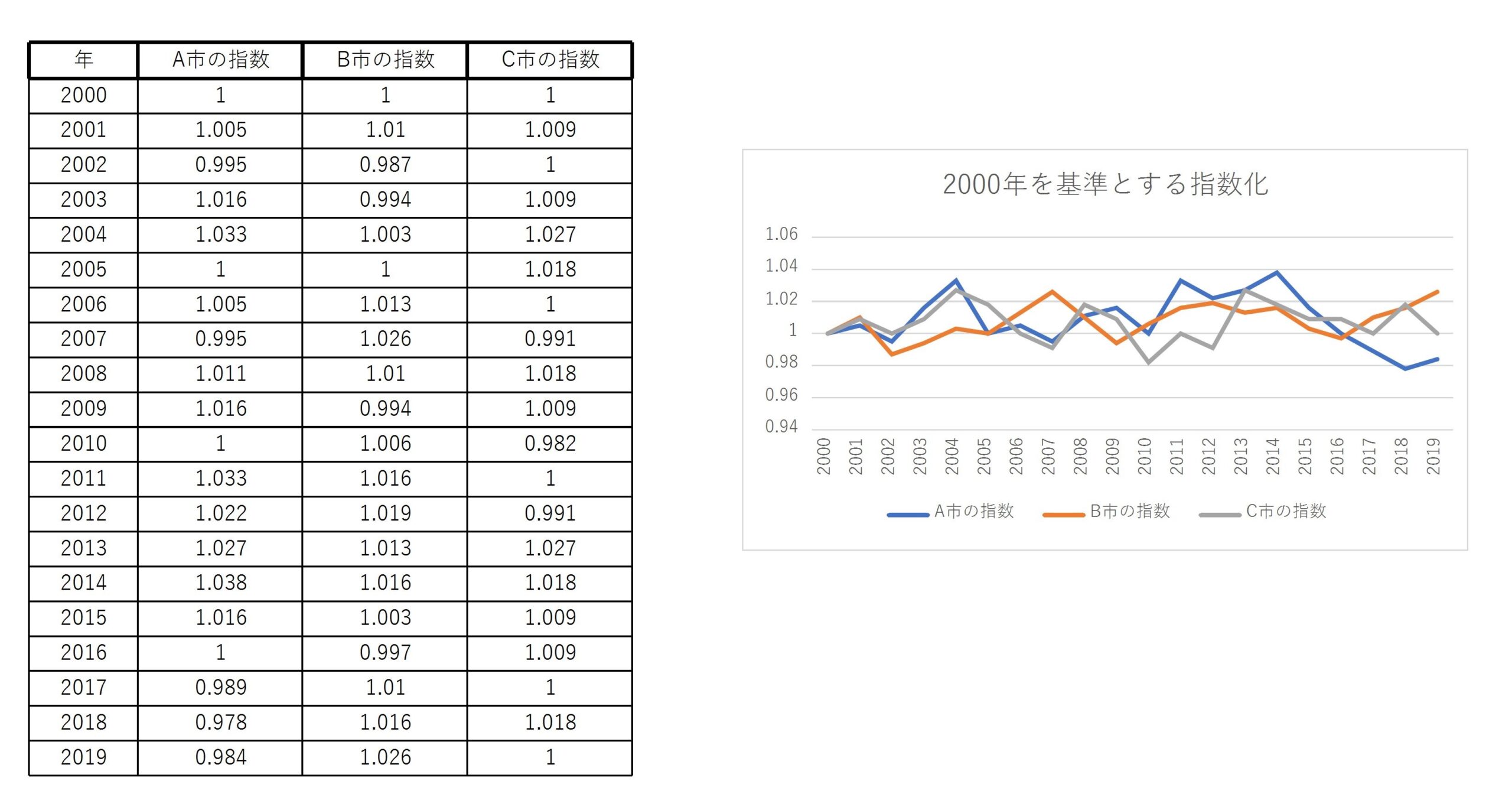
これにより、 各都市が \( 2000 \) 年より人口がどの程度多いか少ないかが他の都市と比較しながら分析できます。
時系列データの変化率・伸び率
今度は、時系列データの変化率・伸び率について紹介します。
各時点でのデータ \( x_0,x_1,\cdots,x_{T-1},x_T \) に対して、変化率 \( p_t \) と伸び率 \( r_t \) を次で定める。
$$ p_t=\frac{x_t-x_{t-1}}{x_{t-1}}, \quad r_t=\frac{x_t}{x_{t-1}} (t=1,2,\cdots,T) $$
つまり、 \( p_t=r_t-1 \) である。
各時点でのデータ \( x_0,x_1,\cdots,x_{T-1},x_T \) に対して、伸び率 \( r_1,r_2,\cdots,r_T \) が与えられたとき、その平均伸び率を計算することを考えてみましょう。
期間 \( [0,T] \) 全体での伸び率は2つの時系列データ \( x_0,x_T \) の伸び率と考えればよいので、 \( \frac{x_T}{x_0} \) で与えられます。
これを変形してみると、
$$ \frac{x_T}{x_0}=\left( \frac{x_1}{x_0} \right)\left( \frac{x_1}{x_2} \right)\cdots \left( \frac{x_T}{x_{T-1}} \right)=r_1r_2\cdots r_T $$
ここで、平均値の常識的な感覚より、求めたい平均伸び率を \( r_G \) とおくと、
$$ \begin{align} \frac{x_T}{x_0}&=r_1r_2\cdots r_T=r_Gr_G\cdots r_G \quad (各r_iをr_Gに置き換えた) \\ &=(r_G)^T \end{align} $$
が成り立つことが予想されます。よって、平均伸び率は
$$ r_G=(r_1r_2\cdots r_T)^{\frac{1}{T}}=\left( \prod_{t=1}^Tr_t \right)^{\frac{1}{T}} $$
となります。この平均の取り方のことを幾何平均といいます。
(ちなみに、いつもの平均の取り方のことは算術平均といいます。)
\( p_t=r_t-1 \) より、平均変化率 \( p_G \) は
$$ p_G=r_G-1 $$
で求められます。
例2のデータを考えます。

これらの変化率・伸び率を求めると次のようになります。(小数点以下第4位を四捨五入)
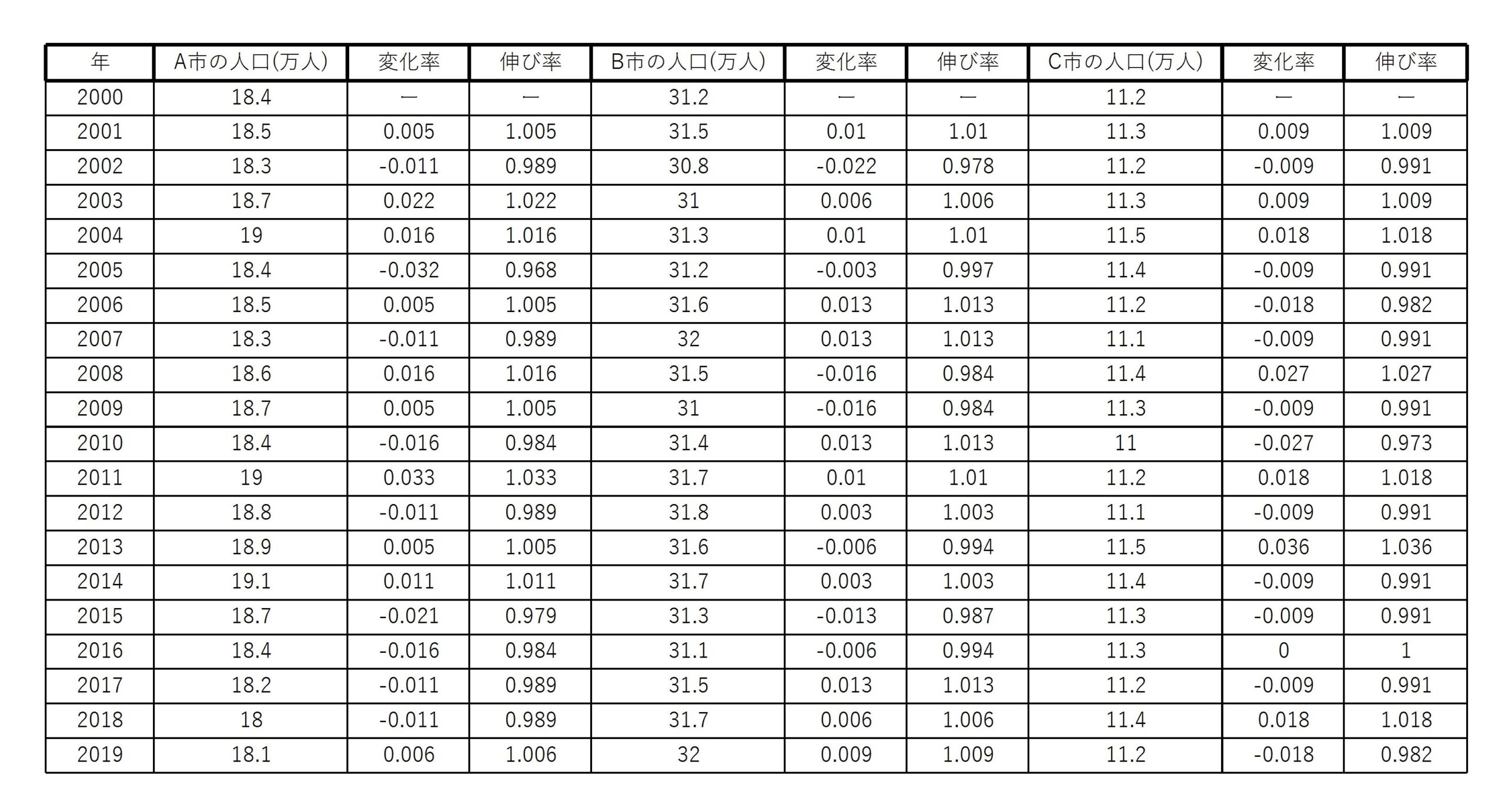
よって、各都市の平均変化率と平均伸び率は、
A都市:平均伸び率 \( r_G=(0.982)^{\frac{1}{19}}=0.999 \) 、平均変化率 \( p_G=r_G-1=-0.001 \)
B都市:平均伸び率 \( r_G=(1.026)^{\frac{1}{19}}=1.001 \) 、平均変化率 \( p_G=r_G-1=0.001 \)
C都市:平均伸び率 \( r_G=(0.997)^{\frac{1}{19}}=1 \) 、平均変化率 \( p_G=r_G-1=0 \)
時系列データの変動分解
株価や年収などの経済や経営に関する時系列データのことを経済時系列データといいます。
経済時系列データは次の3つの変動から構成されているとして、それぞれの変動ごとに分解することを考えます。
経済時系列データは次の3つの変動から構成されていると考える。
(1) 傾向変動(トレンド)(TC):時間の経過とともに上昇もしくは減少するようなデータのこと
(2) 季節変動(周期変動)(S):ある期間を周期として上昇と減少を繰り返すようなデータのこと
(3) 不規則変動(I):時間の経過によらない変動でとらえどころのないデータのこと
傾向変動(トレンド)の移動平均による抽出
トレンドは上昇か減少かで次の2つに分けられます。
次の図のように、時間の経過とともに上昇するトレンドのことを正のトレンドといいます。
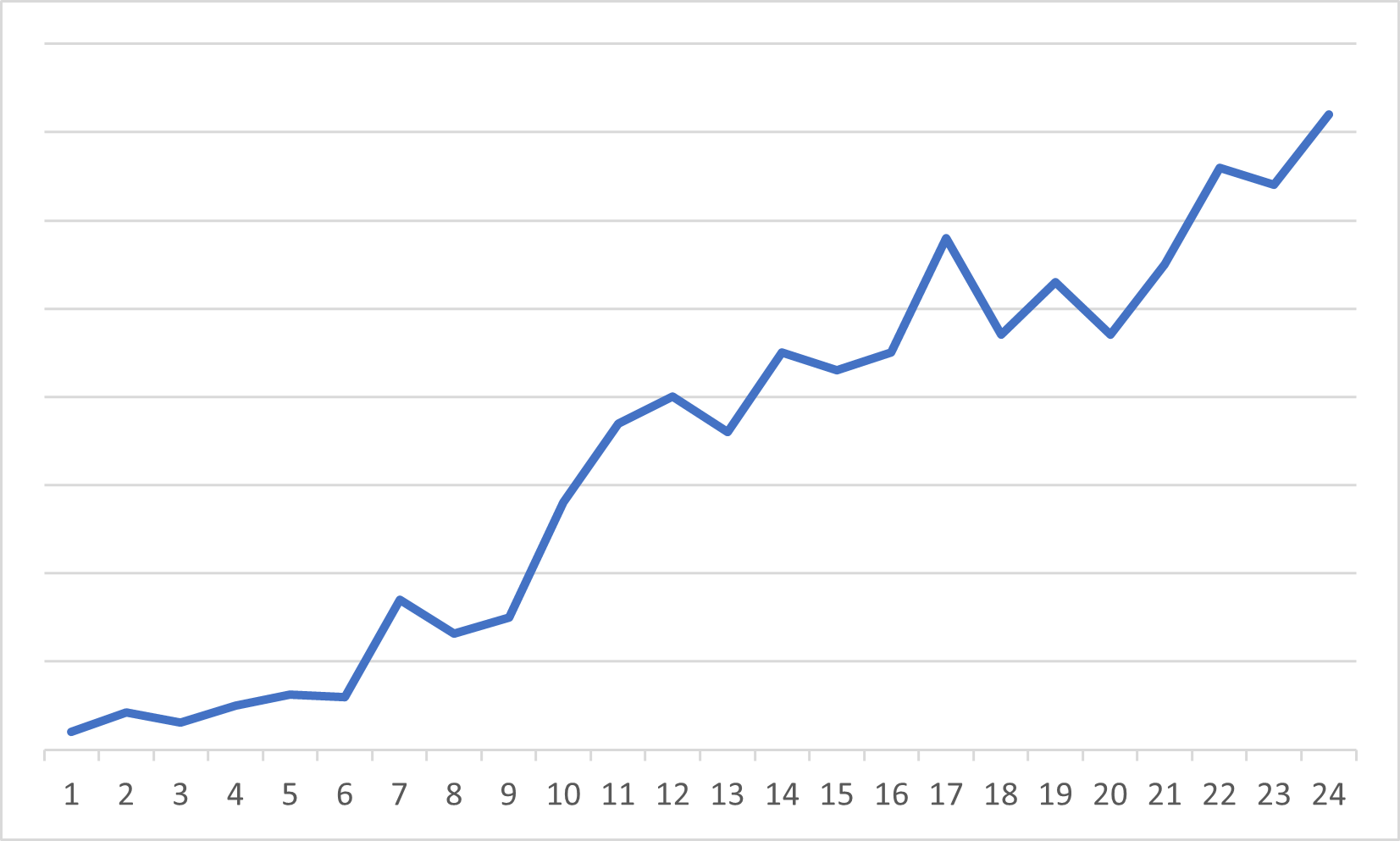
次の図のように、時間の経過とともに減少するトレンドのことを負のトレンドといいます。
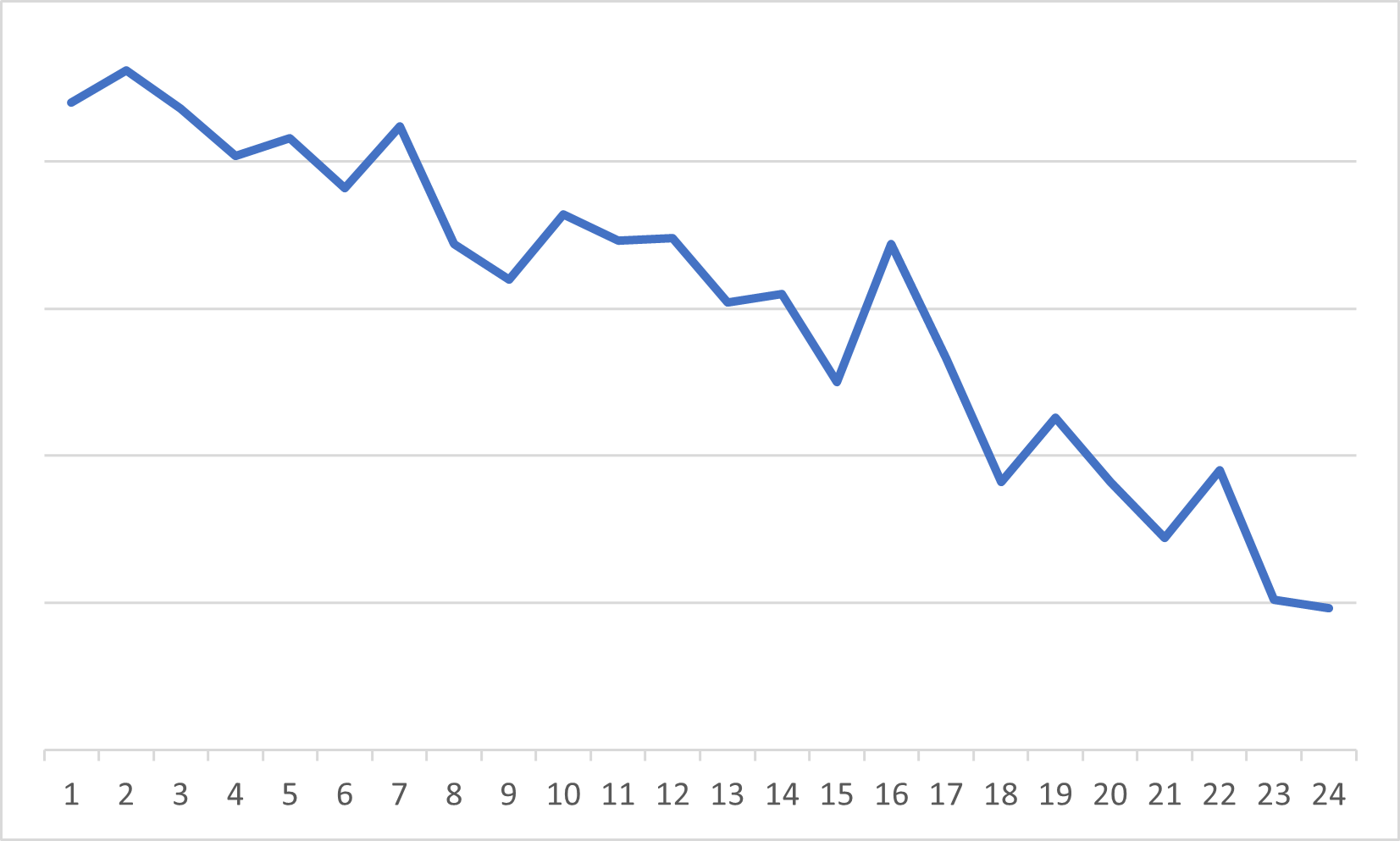
あるガソリンスタンドでのレギュラーガソリンの1Lあたりの値段のデータを考える。
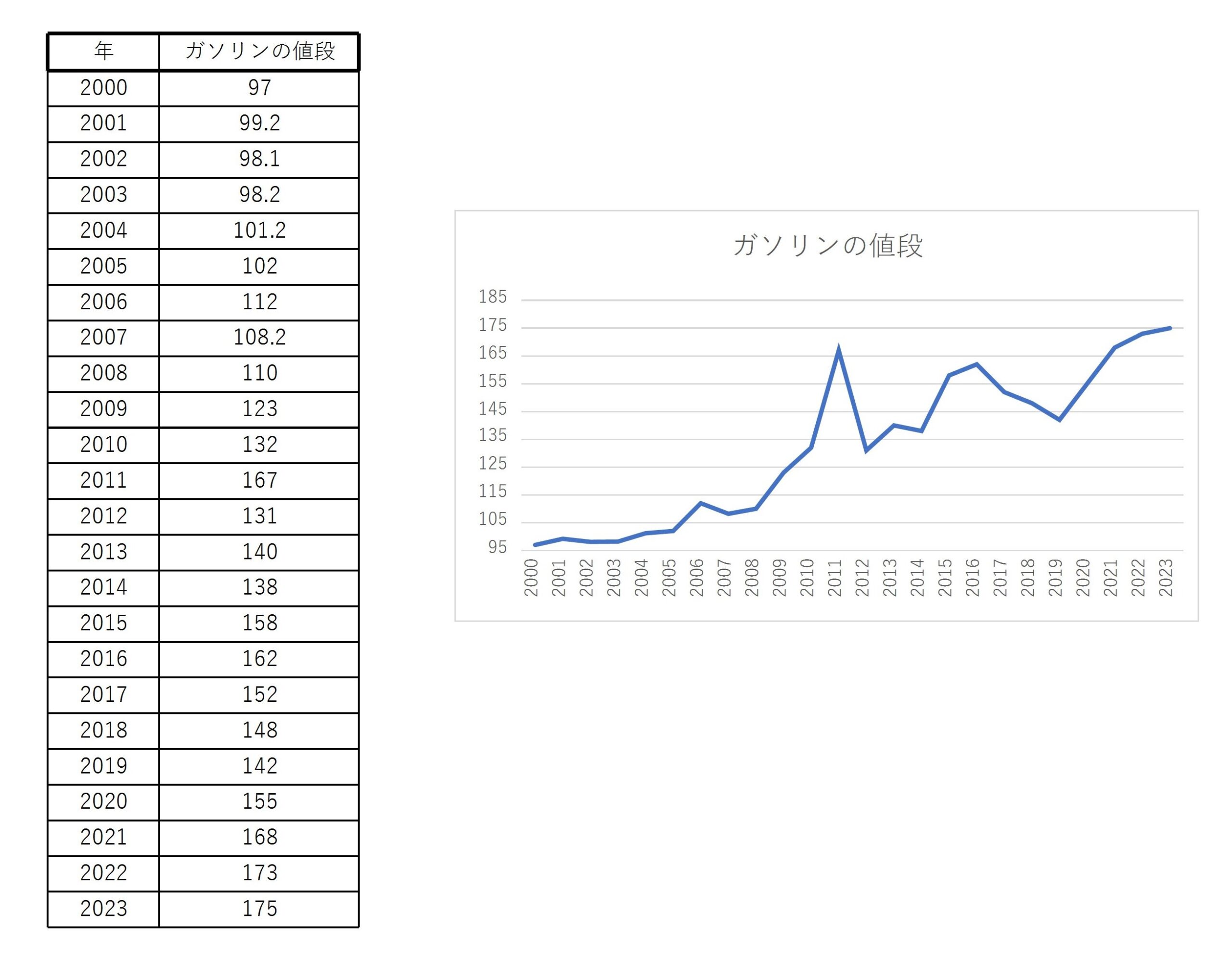
この図より、正のトレンドがあるといえる。
では、与えられた経済時系列データからトレンドの部分だけを抽出するにはどうしたらいいのでしょうか。
その方法はいくつかありますが、ここでは移動平均法について紹介します。
時系列データ \( x_0,x_1,\cdots,x_{T-1},x_T \) のうち、時点 \( t \) での値と \( k \) 時点前から \( k \) 時点後までの \( 2k+1 \) 個のデータ
$$ x_{t-k}, \ x_{t-k+1}, \ \cdots, \ x_t, \ \cdots, \ x_{t+k-1}, \ x_{t+k} $$
を用いて、 \( (2k+1) \) 項移動平均 \( \hat{TC}_t \) を次で定める。
$$ \hat{TC}_t=\sum_{s=t-k}^{t+k}\frac{x_s}{2k+1} $$
これにより、不規則変動と周期 \( 2k+1 \) の季節変動が除去されます。
よく考えられるのは周期12か月の季節変動ですので、 \( 12 \) 項の移動平均を考えたいです。
しかし、 \( 12 \) は \( 2k+1 \) では表せないので、移動平均をすこし修正をします。
\( k=6 \) として、 \( 13 \) 個のデータ
$$ x_{t-6}, \ x_{t-5}, \ \cdots, \ x_t, \ \cdots, \ x_{t+5}, \ x_{t+6} $$
を考えますが、ここで端の点 \( x_{t-6},x_{t+6} \) を \( \frac{x_{t-6}}{2},\frac{x_{t+6}}{2} \) で置き換えます。
そして、移動平均 \( \hat{TC}_t \) を次で求めます。
$$ \hat{TC}_t=\frac{1}{12}\left( \frac{x_{t-6}}{2}+x_{t-5}+\cdots+x_t+\cdots+x_{t+5}+\frac{x_{t+6}}{2} \right) $$
これは
$$ \begin{align} &\frac{1}{12}\left( \frac{x_{t-6}}{2}+x_{t-5}+\cdots+x_t+\cdots+x_{t+5}+\frac{x_{t+6}}{2} \right) \\ &=\frac{1}{24}\{ (x_{t-6}+\cdots+x_{t+5})+(x_{t-5}+\cdots+x_{t+6}) \} \\ &=\frac{1}{2}\left\{ \sum_{s=t-6}^{t+5}\frac{x_s}{12}+\sum_{s=t-5}^{t+6}\frac{x_s}{12} \right\} \end{align} $$
と変形でき、2つの \( 12 \) 項の移動平均の平均値となります。
よって、周期12か月の季節変動を除去することができます。
ある都市の過去3年間(36か月)の平均月収のデータを考える。
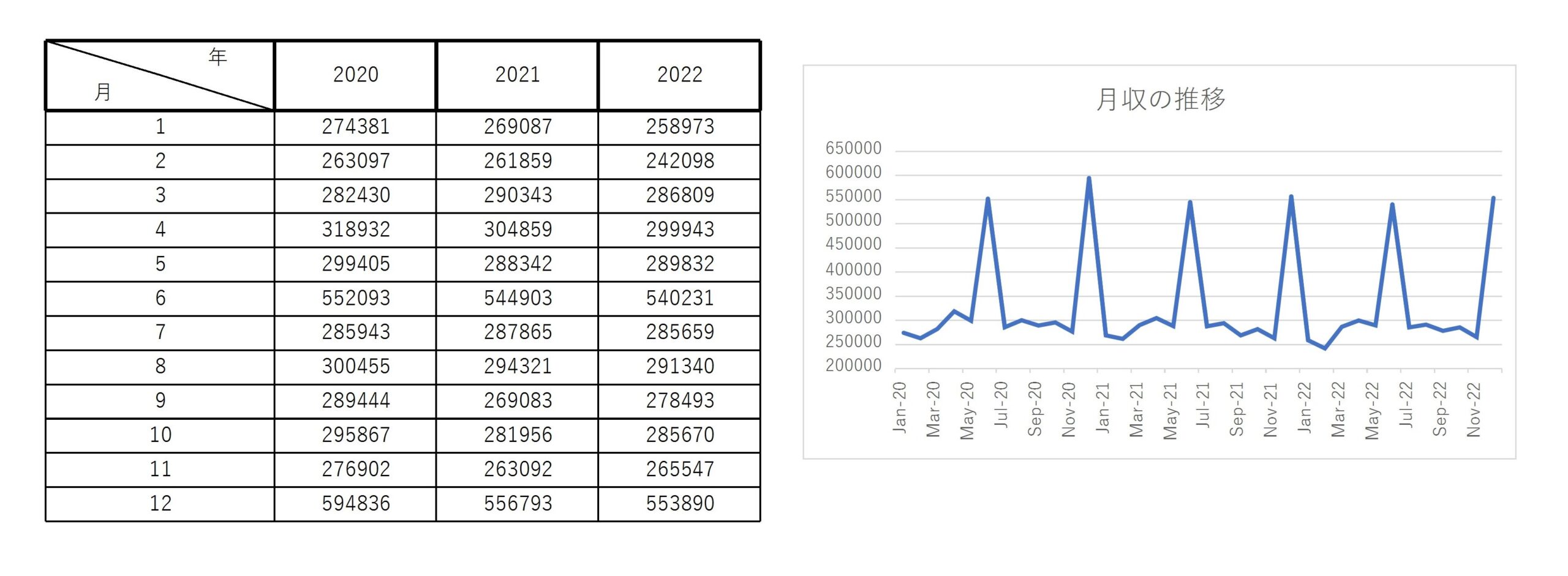
これを \( 12 \) 項の移動平均により、不規則変動と周期12か月の季節変動を除去すると、
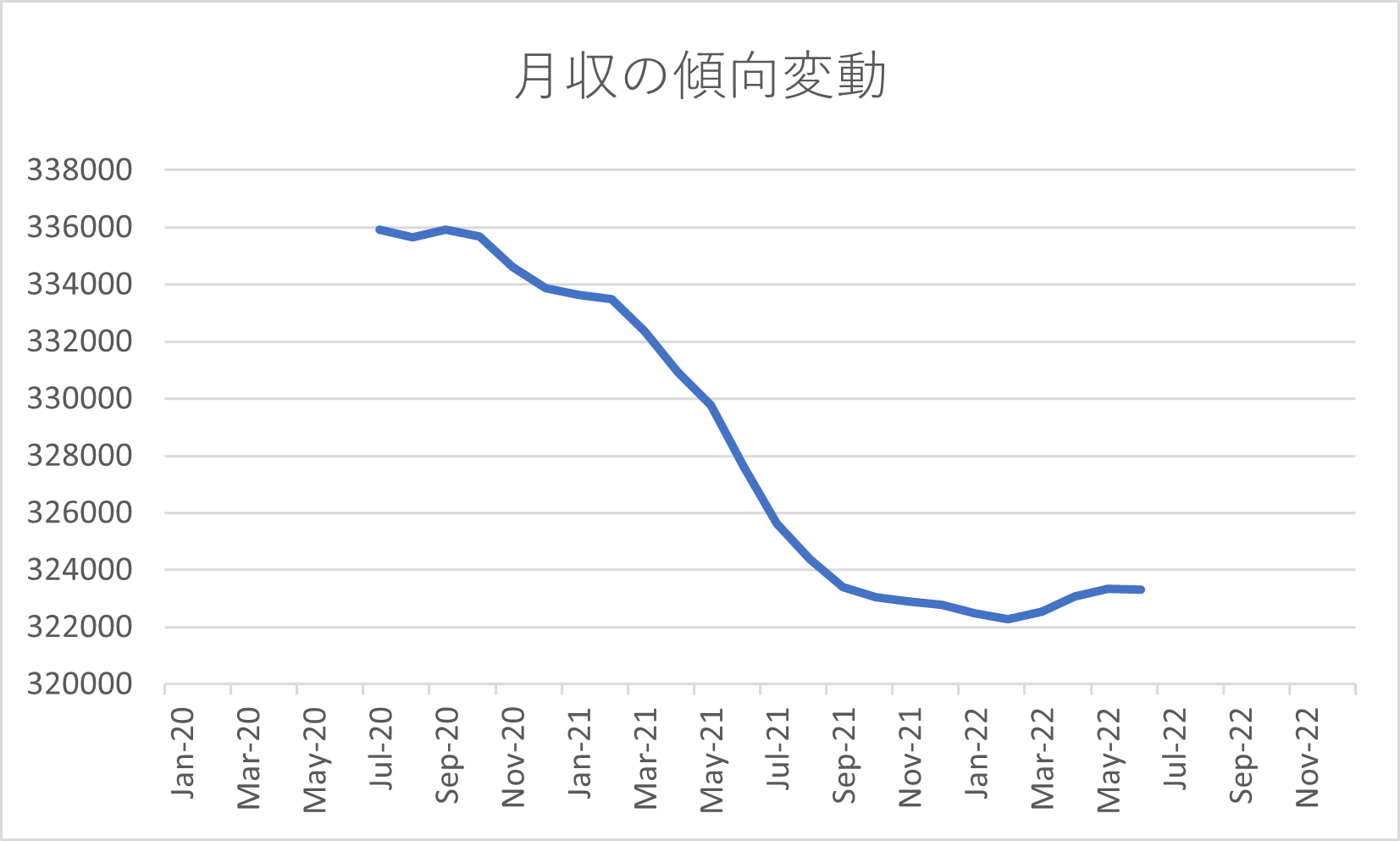
このグラフは傾向変動(トレンド)のみを表しているものとなり、このデータは負のトレンドをもつ。
時系列データの変動分解
それではいよいよ経済時系列データ \( x_0,x_1,\cdots,x_{T-1},x_T \) を傾向変動 \( \hat{TC}_t \) と季節変動 \( \hat{S}_t \) と不規則変動 \( \hat{I}_t \) に分解することを考えます。つまり、
$$ x_t=\hat{TC}_t+\hat{S}_t+\hat{I}_t $$
まず、先ほど紹介した移動平均法により傾向変動 \( \hat{TC}_t \) を抽出します。
そして、 \( w_t=x_t-\hat{TC}_t \) とおくと、これは季節変動と不規則変動を含んでいます。
ここから、季節変動だけ抽出するため(つまり不規則変動を排除するため)に、周期 \( m \) 別での \( w_t \) の平均値 \( \bar{w}_i, \ i=1,2,\cdots,m \) を求めます。
(周期12か月の場合は月別での平均値 \( \bar{w}_1,\cdots,\bar{w}_{12} \) を求めます。たとえば、
$$ \bar{w}_1=\frac{2000年1月のデータ+2001年1月のデータ+\cdots+2020年1月のデータ}{21} $$
を各月で求めるということです。)
そして、各周期内での比較がしやすいように平均を0としたいので、各 \( \bar{w}_i \) から \( \bar{w}_i \) の平均 \( \bar{\bar{w}} \) を引くことにより季節変動 \( \hat{S}_t \) が求まります。
(たとえば、周期12か月の場合は \( \bar{w}_1,\cdots,\bar{w}_{12} \) が得られるので、それの平均 \( \displaystyle \frac{1}{12}\sum_{i=1}^{12}\bar{w}_i \) を引きます。
よって、
$$ \hat{S}_1=\bar{w}_1-\bar{\bar{w}}, \quad \cdots, \quad \hat{S}_{12}=\bar{w}_{12}-\bar{\bar{w}}, \quad \hat{S}_{13}=\bar{w}_1-\bar{\bar{w}}, \quad \cdots $$
となります。)
これで、傾向変動 \( \hat{TC}_t \) と季節変動 \( \hat{S}_t \) が得られるので不規則変動 \( \hat{I}_t \) は
$$ \hat{I}_t=x_t-\hat{TC}_t-\hat{S}_t $$
で得られます。
例5の平均月収のデータを考えます。

まず、例5より傾向変動(トレンド)を抽出したグラフは次で与えられる。
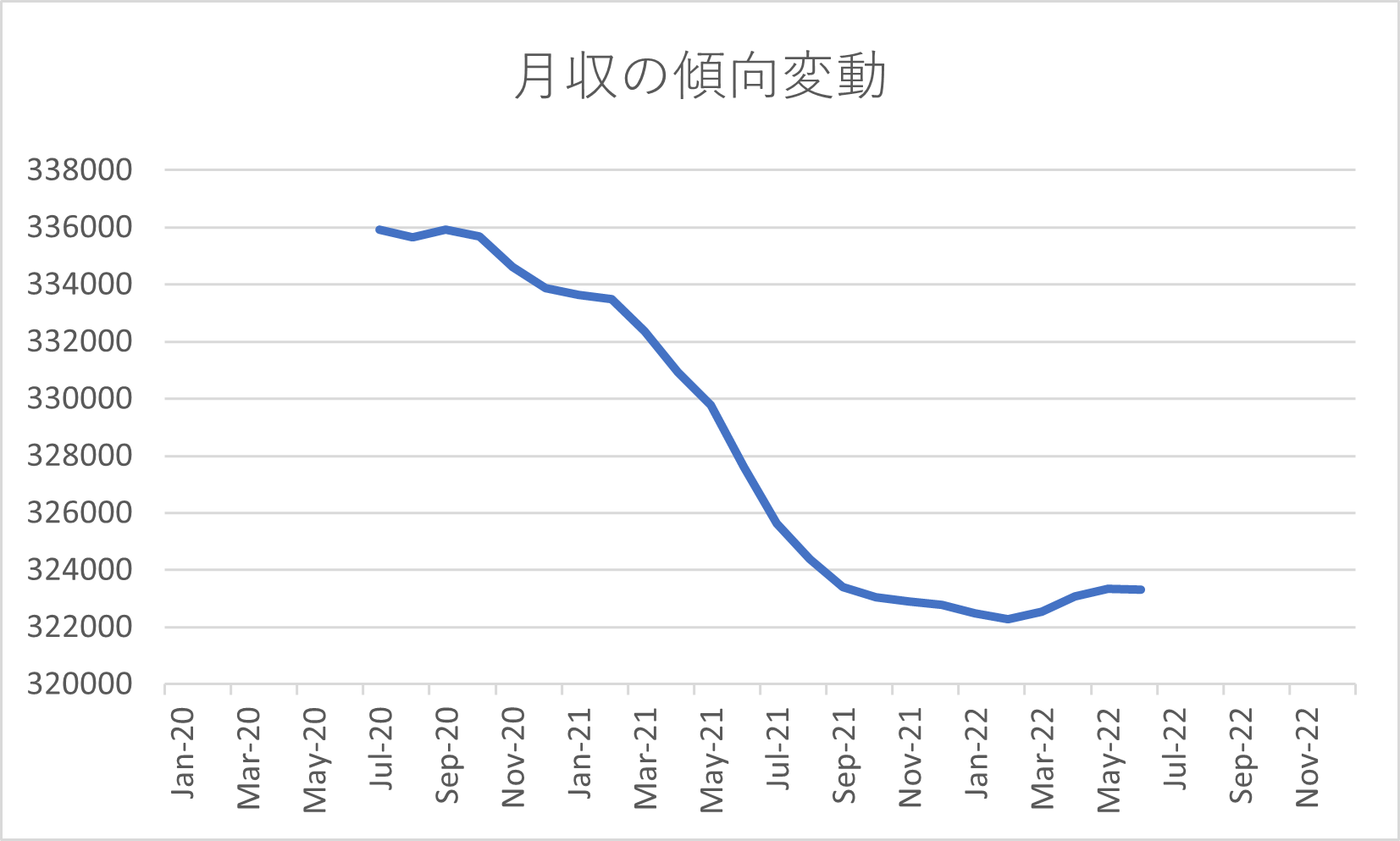
そして、月別の平均を求めることで、季節変動を抽出したグラフは次で与えられる。
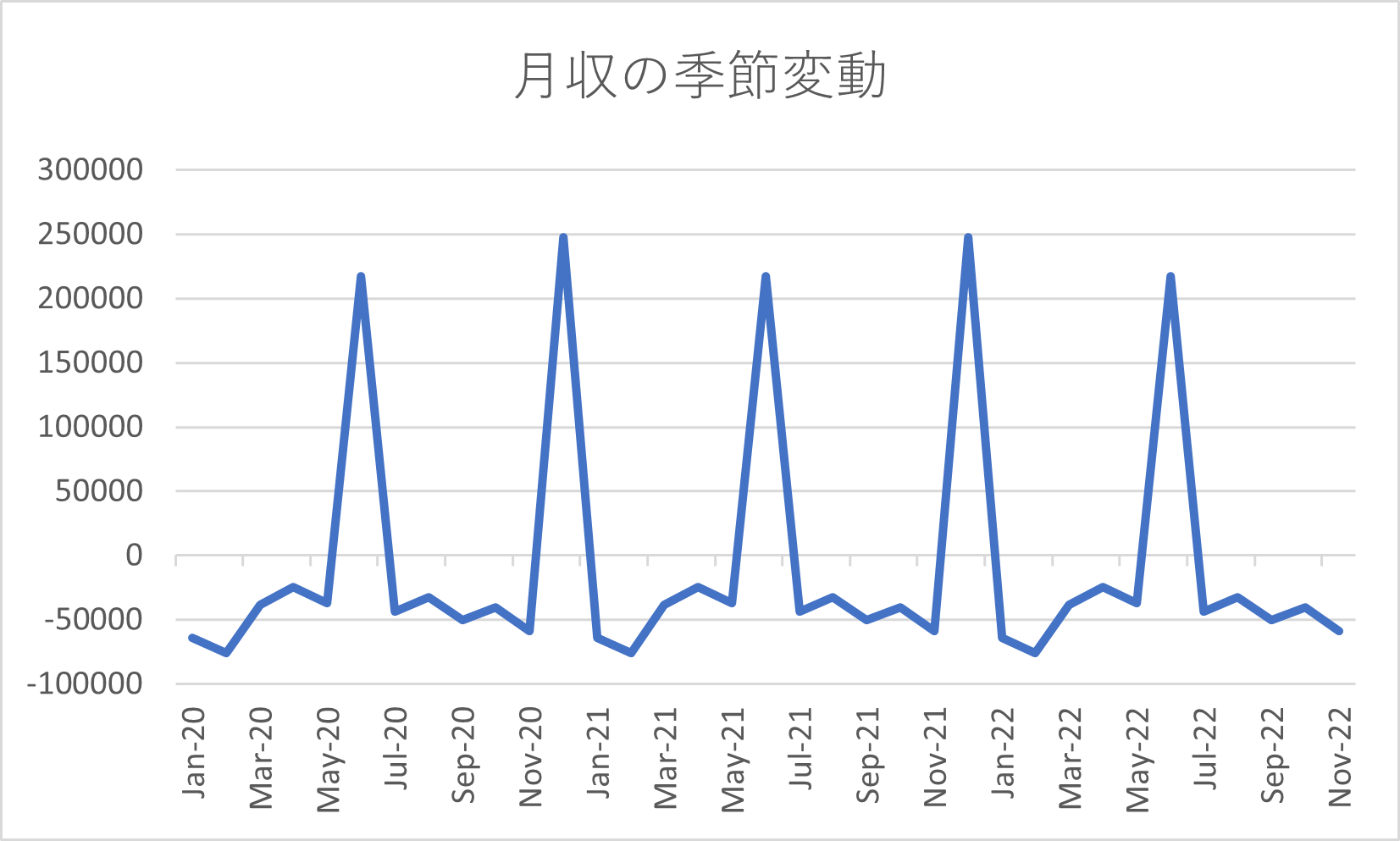
よって、不規則変動のグラフは次で与えられる。
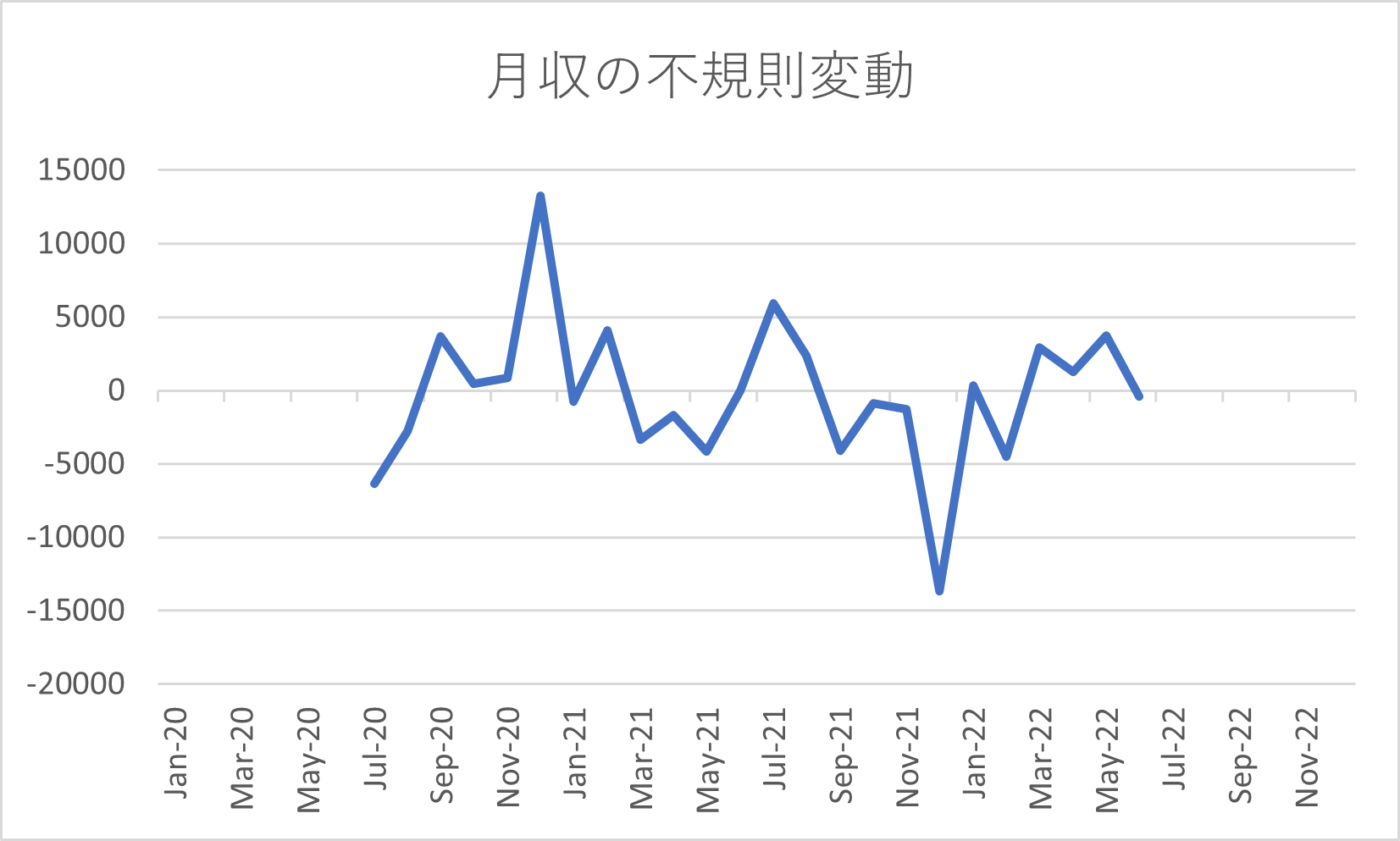
このように、経済時系列データは傾向変動と季節変動と不規則変動の3つに変動分解することができる。
これらから、月収は年々減少傾向にあり、6月と12月はボーナスがある結果月収は増加するということがわかる。
時系列データの自己相関
時系列データを扱う際、1つの時系列データを周期ごとに考えたときに2つの周期の間の相関関係(自己相関)を分析することがあります。
(例えば、各月の平均気温のデータを1年周期で相関関係を調べることで、毎年夏が気温が高く冬に気温が低くなることが分かります。)
そのため、もとのデータ \( x_0,x_1,\cdots,x_{T-1},x_T \) と時点を \( h \) だけずらしたデータ \( x_h,x_{h+1},\cdots,x_{T-1},x_T \) を考えます。
この2つのデータを2変数データ \( \{ (x_t,x_{t+h}) \ | \ t=0,1,\cdots,T \} \) と考えて、この相関係数(自己相関係数)を求めます。
ただし、時系列データの自己相関係数は普通の相関係数とは求め方が違うので注意してください。
時系列データから得られる2変数データ \( \{ (x_t,x_{t+h}) \ | \ t=0,1,\cdots,T \} \) に対して、自己共分散関数を次で定める。
$$ C_h=\frac{1}{T}\sum_{t=1}^{T-h}(x_t-\bar{x})(x_{t+h}-\bar{x}), \quad (h=0,1,2,\cdots) $$
これをもとにして、自己相関係数を次で定める.
$$ r_h=\frac{C_h}{C_0} $$
また、 \( r_h \) を \( h \) の関数としてみたとき、これを自己相関関数といい、 \( h \) のことをラグという。
この自己相関係数 \( r_h \) は、横軸をラグ \( h \) 、縦軸を \( r_h \) としたコレログラムというグラフにて表現することができます。
これにより、周期性がわからないようなデータの周期を推測することもできます。
例5の平均月収のデータを考えます。

このデータのコレログラムは次のようになります。
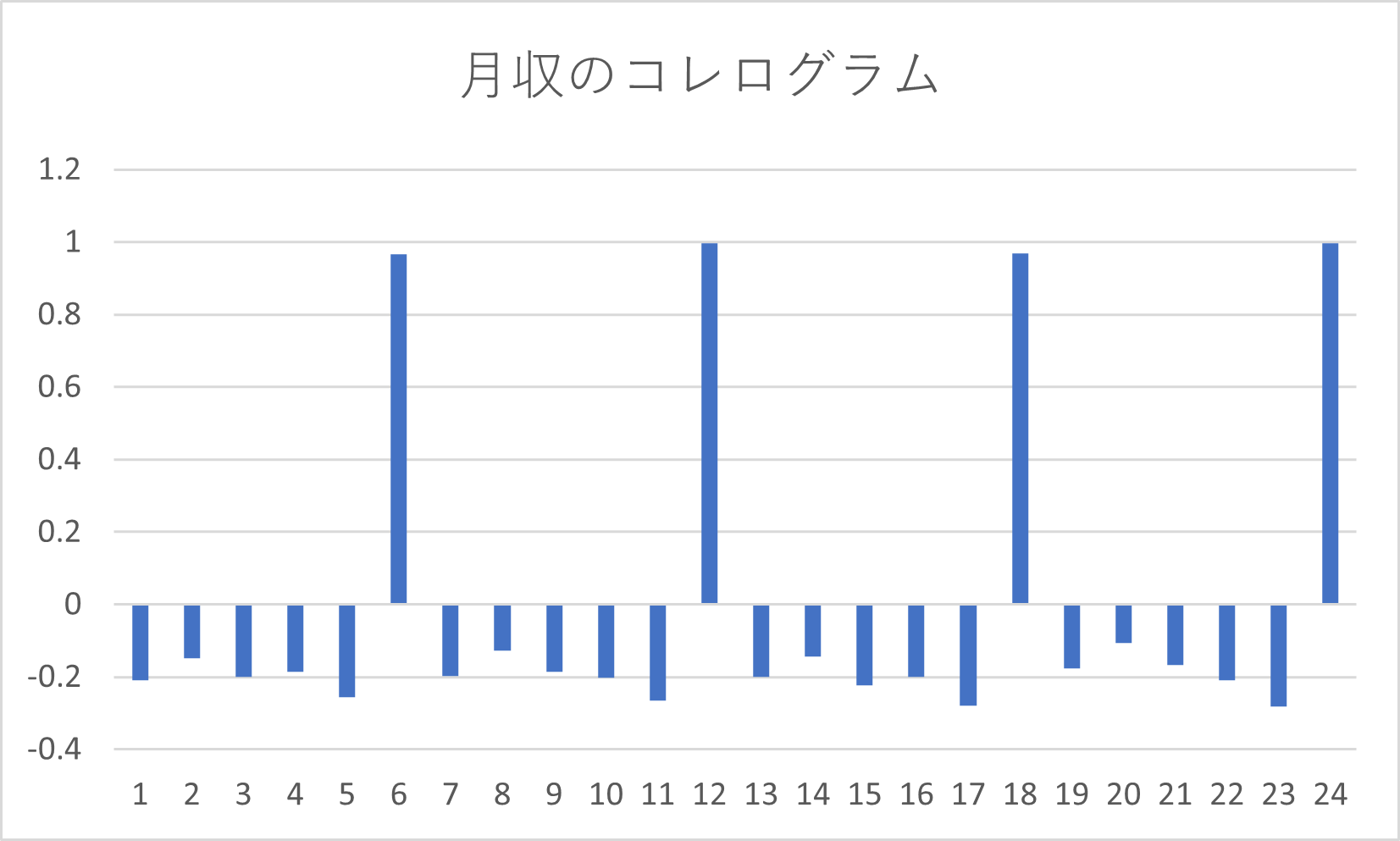
これにより月収は6か月おきに高い相関が見られる。
つまり、半年ごとにボーナスが来て月収が増加する。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

