こんにちは、ひかりです。
今回は確率・統計から最小二乗法による回帰直線の求め方とその性質について解説していきます。
この記事では以下のことを紹介します。
- 相関分析と回帰分析の違いについて
- 最小二乗法による回帰直線の求め方について
- 回帰直線の性質と決定係数について
相関分析と回帰分析の違い
前回の記事で2変数データの間の関係(相関)について紹介しました。
そこでは、2つの変数 \( x,y \) が与えられたときの \( x \) と \( y \) の関係の強弱を見ていきました。
(例えば、数学のテストの点と物理のテストの点が与えられたときにそれらの間にどの程度の関係性があるのかを調べる)
今回は、変数 \( x \) が変数 \( y \) を説明したり予測したりするような方向性をもつ関係(回帰)について考えます。
(例えば、数学のテストの点が与えられたときに物理のテストの点はどのぐらいになるのかを予測する)
このとき、変数 \( x \) を説明変数(独立変数)といい、変数 \( y \) を応答変数(従属変数)といいます。
回帰の考え方のポイントとしては、説明変数 \( x \) と応答変数 \( y \) の間に、
$$ y=ax+b $$
という直線関係を考えて、説明変数 \( x \) から応答変数 \( y \) を予測します。
この直線のことを回帰直線といい、係数 \( a,b \) を回帰係数といいます。
最小二乗法による回帰直線の求め方
それでは、この回帰直線の求め方を見ていきましょう。
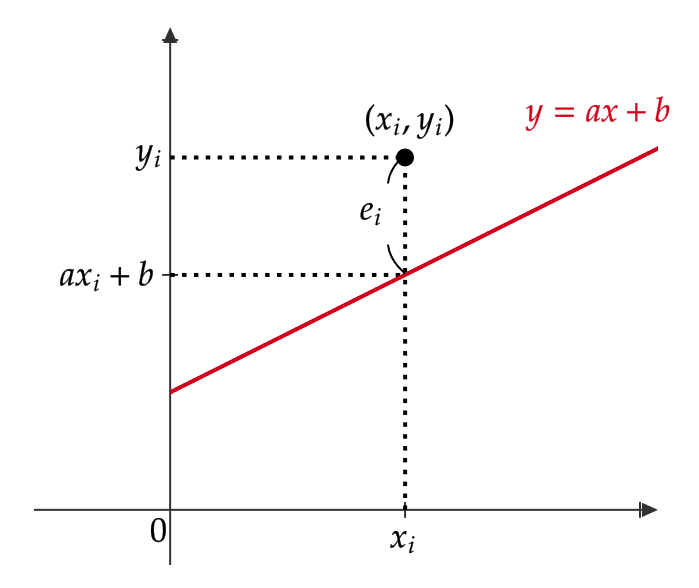
\( n \) 個の2変数データ \( (x_i,y_i) \ (i=1,2,\cdots,n) \) に対して、
$$ e_i=y_i-(ax_i+b) $$
とおきます。
このとき、 \( e_i \) は残差といい、求めたい回帰直線からデータ \( (x_i,y_i) \) がどれほど離れているのかを表しています。
よって、 \( e_i \) を(分散のときと同様に正負が出ないように)2乗したものの \( i \) に関する和を \( a,b \) の2変数関数 \( f(a,b) \) だと思います。つまり、
$$ f(a,b)=\sum_{i=1}^ne_i^2=\sum_{i=1}^n\{ y_i-(ax_i+b)\}^2 $$
(これを残差平方和といいます。)
この関数 \( f(a,b) \) を最小にする点 \( (\hat{a},\hat{b}) \) を考えることにより、 \( n \) 個のデータにもっとも隣接した直線
$$ y=\hat{a}x+\hat{b} $$
を得ることができます。
このようにして、回帰直線を求めることを最小二乗法といいます。
それでは、関数 \( f(a,b) \) を最小にする点 \( (\hat{a},\hat{b}) \) を実際に求めてみましょう。
最小となる点の候補は、関数 \( f(a,b) \) のそれぞれの変数での偏微分の値が0である点となります。(詳しくは微分積分学10の記事をご覧ください。)
つまり、
$$ \frac{\partial f}{\partial a}(\hat{a},\hat{b})=0, \quad \frac{\partial f}{\partial b}(\hat{a},\hat{b})=0 $$
(候補なので必ず最小となる点になるとは限りませんが、実はこの関数の場合は必ず最小となる点になることが知られています。)
この2つの式を計算すると、
$$ \frac{\partial f}{\partial a}(\hat{a},\hat{b})=-2\sum_{i=1}^n\{ y_i-(\hat{a}x_i+\hat{b})\}x_i=0 $$
$$ \frac{\partial f}{\partial b}(\hat{a},\hat{b})=-2\sum_{i=1}^n\{ y_i-(\hat{a}x_i+\hat{b})\}=0 $$
これらをまとめると、
$$ \begin{cases} \hat{a}\sum_{i=1}^nx_i^2+\hat{b}\sum_{i=1}^nx_i=\sum_{i=1}^nx_iy_i \\ \hat{a}\sum_{i=1}^nx_i+n\hat{b}=\sum_{i=1}^ny_i \end{cases} \tag{1} $$
となります。これを正規方程式ということもあります。
第2式を \( n \) で割ると、
$$ \begin{align} 0&=\frac{\hat{a}}{n}\sum_{i=1}^nx_i+\hat{b}-\frac{1}{n}\sum_{i=1}^ny_i \\ &=\hat{a}\bar{x}+\bar{b}-\bar{y} \quad (\bar{x},\bar{y} \ は \ x_i,y_i \ の平均値) \end{align} $$
したがって、
$$ \hat{b}=\bar{y}-\hat{a}\bar{x} $$
これを式(1)に代入すると、
$$ \begin{cases} \hat{a}\sum_{i=1}^nx_i^2+\bar{y}\sum_{i=1}^nx_i-\hat{a}\bar{x}\sum_{i=1}^nx_i=\sum_{i=1}^nx_iy_i \\ \hat{a}\sum_{i=1}^nx_i+n\bar{y}-n\hat{a}\bar{x}=\sum_{i=1}^ny_i \end{cases} $$
第2式の両辺に \( \bar{x} \) をかけると、
$$ \hat{a}\bar{x}\sum_{i=1}^nx_i+n\bar{x}\bar{y}-n\hat{a}\bar{x}^2=\bar{x}\sum_{i=1}^ny_i $$
となるので、第1式とこの式を辺々足すと、
$$ \hat{a}\sum_{i=1}^nx_i^2+\bar{y}\sum_{i=1}^nx_i+n\bar{x}\bar{y}-n\hat{a}\bar{x}^2=\sum_{i=1}^nx_iy_i+\bar{x}\sum_{i=1}^ny_i $$
となります。
$$ \bar{y}\sum_{i=1}^nx_i=\bar{x}\sum_{i=1}^ny_i $$
であることに注意して、まとめると、
$$ \hat{a}=\frac{\sum_{i=1}^nx_iy_i-n\bar{x}\bar{y}}{\sum_{i=1}^nx_i^2-n\bar{x}^2} $$
これをわかりやすいように変形していきます。まず、分子は
$$ \begin{align} \sum_{i=1}^nx_iy_i-n\bar{x}\bar{y}&=\sum_{i=1}^nx_iy_i-n\bar{x}\bar{y}-n\bar{x}\bar{y}+n\bar{x}\bar{y} \\ &=\sum_{i=1}^nx_iy_i-\bar{y}\sum_{i=1}^nx_i-\bar{x}\sum_{i=1}^ny_i+n\bar{x}\bar{y} \\ &=\sum_{i=1}^n(x_iy_i-x_i\bar{y}-\bar{x}y_i+\bar{x}\bar{y}) \\ &=\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})=s_{xy} \end{align} $$
ここで、 \( s_{xy} \) は2変数データ \( (x_i,y_i) \) の共分散となります。
また、分母は
$$ \begin{align} \sum_{i=1}^nx_i^2-n\bar{x}^2&=\sum_{i=1}^nx_i^2-2n\bar{x}^2+n\bar{x}^2 \\ &=\sum_{i=1}^nx_i^2-2\bar{x}\sum_{i=1}^nx_i+n\bar{x}^2 \\ &=\sum_{i=1}^n(x_i^2-2x_i\bar{x}+\bar{x}^2) \\ &=\sum_{i=1}^n(x_i-\bar{x})^2=s_x^2 \end{align} $$
ここで、 \( s_x^2 \) は変数 \( x \) での分散となります。
よって、まとめると、
$$ \hat{a}=\frac{s_{xy}}{s_x^2}=r_{xy}\frac{s_y}{s_x}, \quad \hat{b}=\bar{y}-\hat{a}\bar{x}=\bar{y}-\frac{s_{xy}}{s_x^2}\bar{x} $$
ここで、 \( r_{xy}=\frac{s_{xy}}{s_xs_y} \) は相関係数である。
したがって、次のことが成り立ちます。
\( x_i \) が少なくとも1つは異なるような \( n \) 個の2変数データ \( (x_i,y_i) \ (i=1,2,\cdots,n) \) に対して、その回帰直線は次のようになる。
$$ y-\bar{y}=\frac{s_{xy}}{s_x^2}(x-\bar{x})=r_{xy}\frac{s_y}{s_x}(x-\bar{x}) $$
前回の記事でも扱った20人の数学と物理のテストの点のデータを考える。
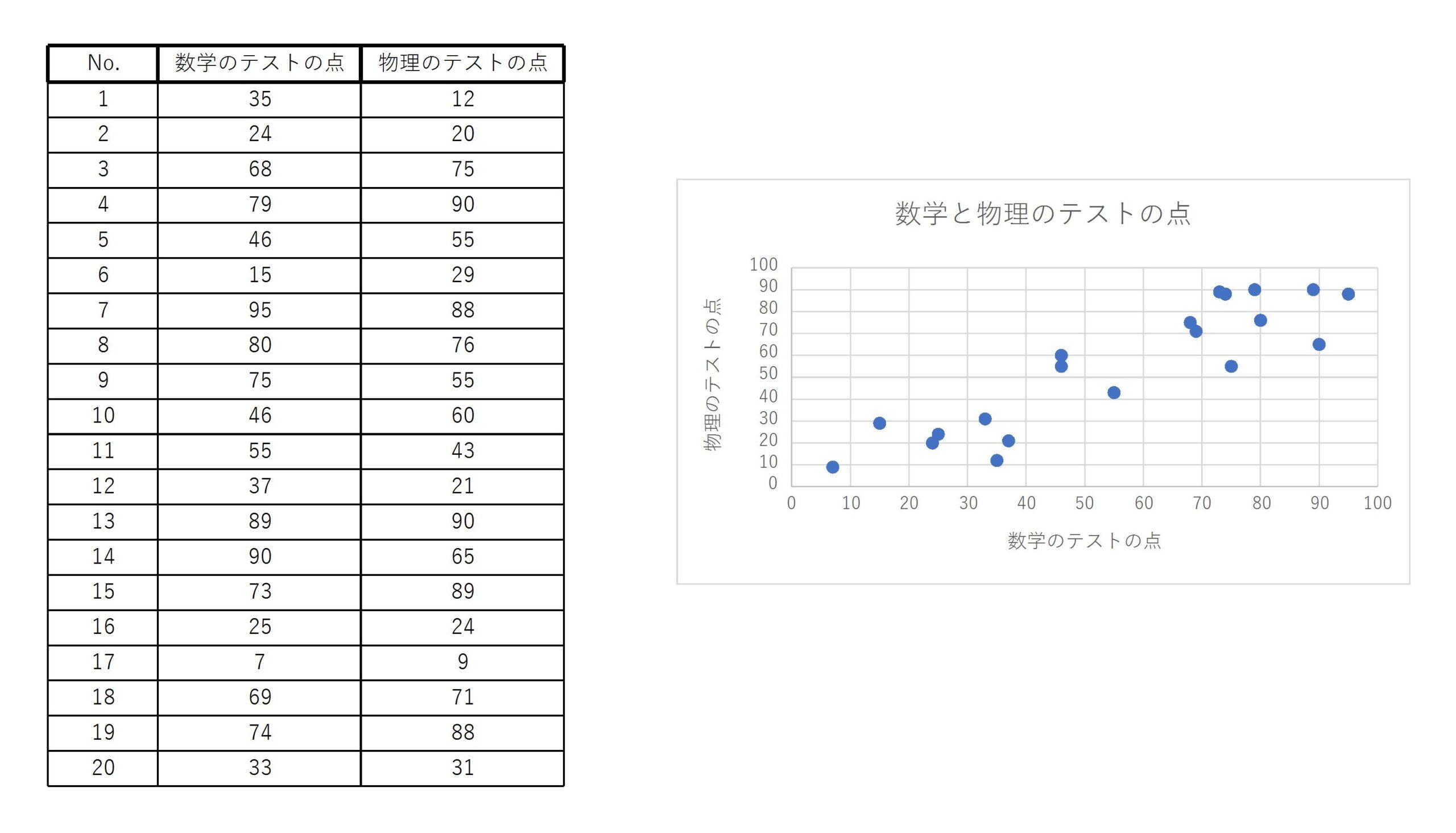
このデータは
$$ \bar{x}=55.75, \quad \bar{y}=54.55, \quad s_x^2=687.79, \quad s_{xy}=658.64 \quad (小数点第三位を四捨五入) $$
よって、回帰直線を求めると、
$$ y-54.55=\frac{658.64}{687.79}(x-55.75) $$
より、
$$ y=0.96x+1.03 $$
この回帰直線から、例えば数学のテストの点が60点であるとすると、物理のテストの点が58.63点ぐらいになると予測することができる。
回帰直線の性質と決定係数
回帰直線の性質
まず、回帰直線の性質を紹介します。
(1) 予測値 \( \hat{y}_i=\hat{a}x_i+\hat{b} \) の平均値はもとのデータ \( y_i \) の平均値と等しい。
(2) 残差 \( e_i=y_i-\hat{y}_i \) の平均値は0である。
(3) 回帰直線は点 \( (\bar{x},\bar{y}) \) を通る。
(4) 予測値 \( \hat{y}_i=\hat{a}x_i+\hat{b} \) と残差 \( e_j \) の相関係数は0である。
(5) (平方和の分解)
$$ \sum_{i=1}^n(y_i-\bar{y})^2=\sum_{i=1}^n(\hat{y}_i-\bar{y})^2+\sum_{i=1}^n(y_i-\hat{y}_i)^2 $$
つまり、応答変数 \( y \) の変動の大きさを表す平方和 \( S_y \) は回帰による平方和 \( S_R \) と残差平方和 \( S_e \) の和
$$ S_y=S_R+S_e $$
に分解される。
定理2の証明(気になる方だけクリックしてください)
(1) 式(1)の第2式を \( n \) で割ると、
$$ \frac{1}{n}\hat{a}\sum_{i=1}^nx_i+\hat{b}=\frac{1}{n}\sum_{i=1}^ny_i $$
であるので、
$$ \bar{\hat{y}}=\frac{1}{n}\sum_{i=1}^n\hat{y}_i=\frac{1}{n}\sum_{i=1}^n(\hat{a}x_i+\hat{b})=\frac{1}{n}\hat{a}\sum_{i=1}^nx_i+\hat{b}=\frac{1}{n}\sum_{i=1}^ny_i=\bar{y} $$
(2) (1)より、 \( \bar{\hat{y}}=\bar{y} \) より、
$$ \bar{e}=\frac{1}{n}\sum_{i=1}^ne_j=\frac{1}{n}\sum_{i=1}^n(y_i-\hat{y}_i)=\frac{1}{n}\sum_{i=1}^ny_i-\frac{1}{n}\sum_{i=1}^n\hat{y}_i=\bar{y}-\bar{\hat{y}}=0 $$
(3) 回帰直線の式
$$ y-\bar{y}=\frac{s_{xy}}{s_x^2}(x-\bar{x})=r_{xy}\frac{s_y}{s_x}(x-\bar{x}) $$
より、 \( x=\bar{x} \) を代入すると、 \( y-\bar{y}=0 \) となります。
よって、 \( y=\bar{y} \) となり、点 \( (\bar{x},\bar{y}) \) は回帰直線上にあります。
(4) まず、予測値 \( \hat{y} \) と残差 \( e \) との共分散 \( s_{\hat{y}e} \) を求めると、
$$ y_i-\bar{y}=\hat{a}(x_i-\bar{x}) $$
と \( \bar{e}=0 \) より、
$$ \begin{align} s_{\hat{y}e}&=\frac{1}{n}\sum_{i=1}^n(\hat{y}_i-\bar{y})(e_i-\bar{e})=\frac{1}{n}\sum_{i=1}^n\hat{a}(x_i-\bar{x})e_i \\ &=\frac{\hat{a}}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\hat{y}_i) \end{align} $$
ここで、
$$ \hat{y}_i=\hat{a}x_i+\hat{b}=\hat{a}x_i+\bar{y}-\hat{a}\bar{x}=\bar{y}+\hat{a}(x_i-\bar{x}) $$
より、さらに計算をすると、
$$ \begin{align} \frac{\hat{a}}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\hat{y}_i)&=\frac{\hat{a}}{n}\sum_{i=1}^n(x_i-\bar{x})\{ y_i-(\bar{y}+\hat{a}(x_i-\bar{x}))\} \\ &=\frac{\hat{a}}{n}\left\{ \sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})-\hat{a}\sum_{i=1}^n(x_i-\bar{x})^2 \right\} \\ &=\hat{a}(s_{xy}-\hat{a}s_x^2) \end{align} $$
ここで、 \( \hat{a}=\frac{s_{xy}}{s_x^2} \) であるので、
$$ s_{\hat{y}e}=\hat{a}(s_{xy}-\hat{a}s_x^2)=\frac{s_{xy}}{s_x^2}\left(s_{xy}-\frac{s_{xy}}{s_x^2}s_x^2\right)=0 $$
したがって、相関係数 \( r_{\hat{y}e} \) は、
$$ r_{\hat{y}e}=\frac{s_{\hat{y}e}}{s_{\hat{y}}s_e}=0 $$
(5)
$$ \begin{align} \sum_{i=1}^n(y_i-\bar{y})^2&=\sum_{i=1}^n\{ (y_i-\hat{y}_i)+(\hat{y}_i-\bar{y})\}^2 \\ &=\sum_{i=1}^n(y_i-\hat{y}_i)^2+\sum_{i=1}^n(\hat{y}_i-\bar{y})^2+2\sum_{i=1}^n(y_i-\hat{y}_i)(\hat{y}_i-\bar{y}) \end{align} $$
ここで、最右辺の第3項は
$$ \sum_{i=1}^n(y_i-\hat{y}_i)(\hat{y}_i-\bar{y})=\sum_{i=1}^ne_i(\hat{y}_i-\bar{y})=\sum_{i=1}^n(\hat{y}_i-\bar{y})(e_i-\bar{e})=ns_{\hat{y}e} $$
(4)より、 \( s_{\hat{y}e}=0 \) であるので、
$$ \sum_{i=1}^n(y_i-\bar{y})^2=\sum_{i=1}^n(y_i-\hat{y}_i)^2+\sum_{i=1}^n(\hat{y}_i-\bar{y})^2 $$
決定係数
定理2の(5)より、 \( r^2=\frac{S_R}{S_y} \) とおくと、
$$ S_e=S_y-S_R=\left( 1-\frac{S_R}{S_y} \right) S_y=(1-r^2)\sum_{i=1}^n(y_i-\bar{y})^2 $$
よって、
$$ \sum_{i=1}^n(y_i-\hat{y}_i)^2=(1-r^2)\sum_{i=1}^n(y_i-\bar{y})^2 $$
となります。よって、 \( r^2 \) が1に近いほど \( y_i \) は \( \hat{y}_i \) に近づいていき、 \( r^2=1 \) のときは \( y_i=\hat{y}_i \) となり回帰直線は、
$$ y_i=\hat{a}x_i+\hat{b} $$
となるので、 \( y_i \) は \( x_i \) から完全に決定されます。
よって、 \( r^2 \) は \( x \) が \( y \) を決定する強弱の度合いを表しています。そのため、 \( r^2 \) のことを決定係数といいます。
\( n \) 個の2変数データ \( (x_i,y_i) \ (i=1,2,\cdots,n) \) の変動係数を \( r_{xy} \) とおくと、決定係数 \( r^2 \) は次で与えられる。
$$ r^2=r_{xy}^2 $$
定理3の証明(気になる方だけクリックしてください)
回帰直線
$$ \hat{y}_i-\bar{y}=r_{xy}\frac{s_y}{s_x}(x_i-\bar{x}) $$
より、
$$ \begin{align} \sum_{i=1}^n(\hat{y}_i-\bar{y})^2&=\sum_{i=1}^n\left\{ r_{xy}\frac{s_y}{s_x}(x_i-\bar{x}) \right\}^2 \\ &=\left( r_{xy}\frac{s_y}{s_x} \right)^2\sum_{i=1}^n(x_i-\bar{x})^2 \\ &=r_{xy}^2\cdot ns_y^2=r_{xy}^2\sum_{i=1}^n(y_i-\bar{y})^2 \end{align} $$
よって、定理2の(5)と組み合わせると、
$$ \begin{align} \sum_{i=1}^n(y_i-\bar{y})^2&=\sum_{i=1}^n(\hat{y}_i-\bar{y})^2+\sum_{i=1}^n(y_i-\hat{y}_i)^2 \\ &=r_{xy}^2\sum_{i=1}^n(y_i-\bar{y})^2+\sum_{i=1}^n(y_i-\hat{y}_i)^2 \end{align} $$
したがって、
$$ \sum_{i=1}^n(y_i-\hat{y}_i)^2=(1-r_{xy}^2)\sum_{i=1}^n(y_i-\bar{y})^2 $$
となるので、 \( r^2=r_{xy}^2 \) となります。
例1の20人の数学と物理のテストの点のデータを考える。

決定係数 \( r^2 \) を求めるために共分散 \( r_{xy} \) を求めると、
$$ r_{xy}=0.90 \quad (小数点第三位を四捨五入) $$
したがって、
$$ r^2=r_{xy}^2=0.81 $$
となるので、例1で求めた回帰直線はデータの本質をある程度とらえているといえる。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

