こんにちは、ひかりです。
今回は確率・統計から質的データと2変数データの表現と分析について解説していきます。
この記事では以下のことを紹介します。
- 質的データの表現について
- 2変数データの記述について
質的データの表現
前回の記事にて、量的データについて紹介しました。
今回は、質的変数のデータである質的データの表現について見ていきましょう。
まず、度数と相対度数については、量的データと同様に考えることができます。
質的データをカテゴリーごとに分類したとき、同じカテゴリーに属するデータの数を度数という。
また、各度数を度数の総和で割ったものを相対度数という。
20人のある講義の成績を表したデータがある。
このとき、度数と相対度数の表は次のように書ける。
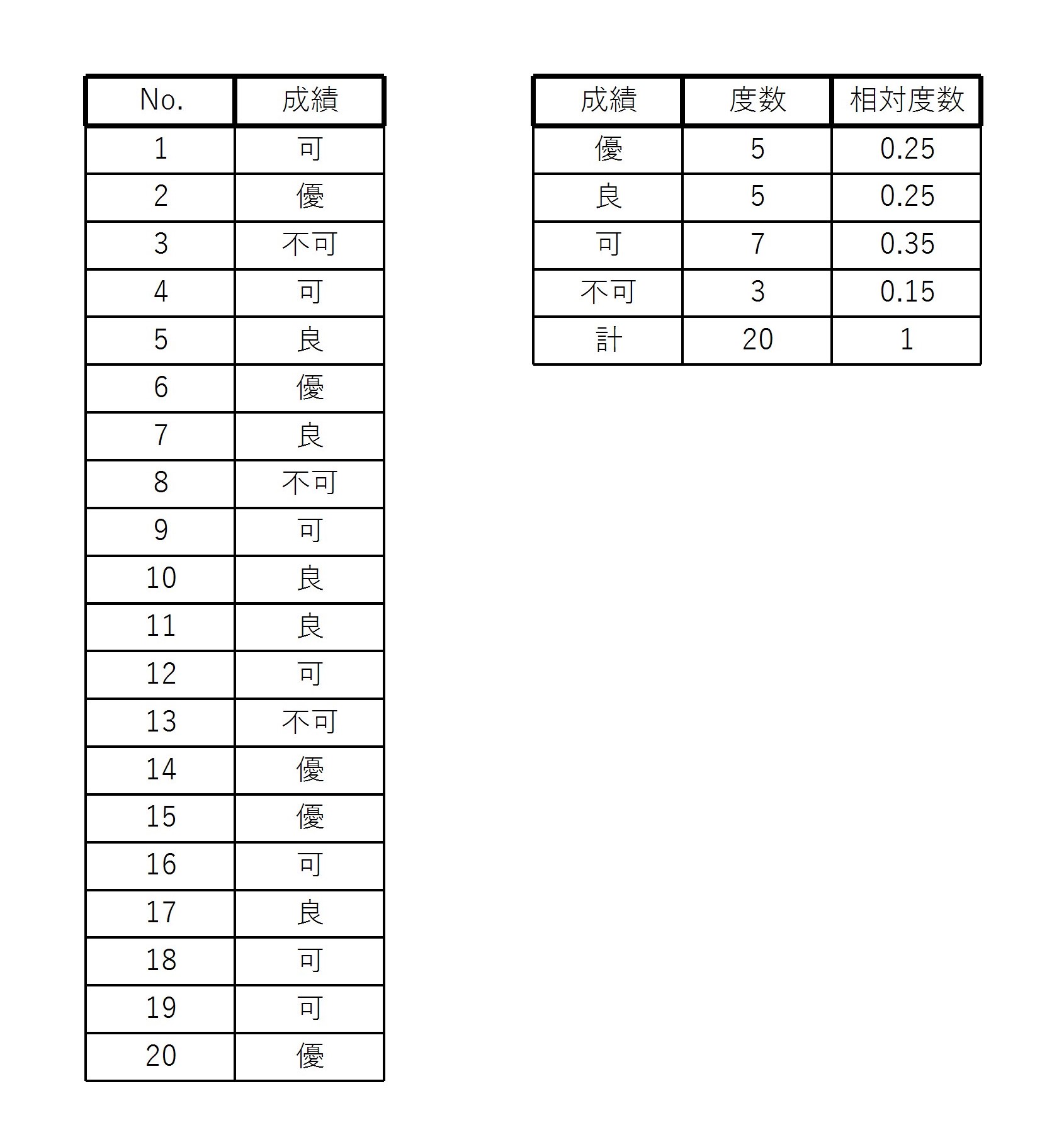
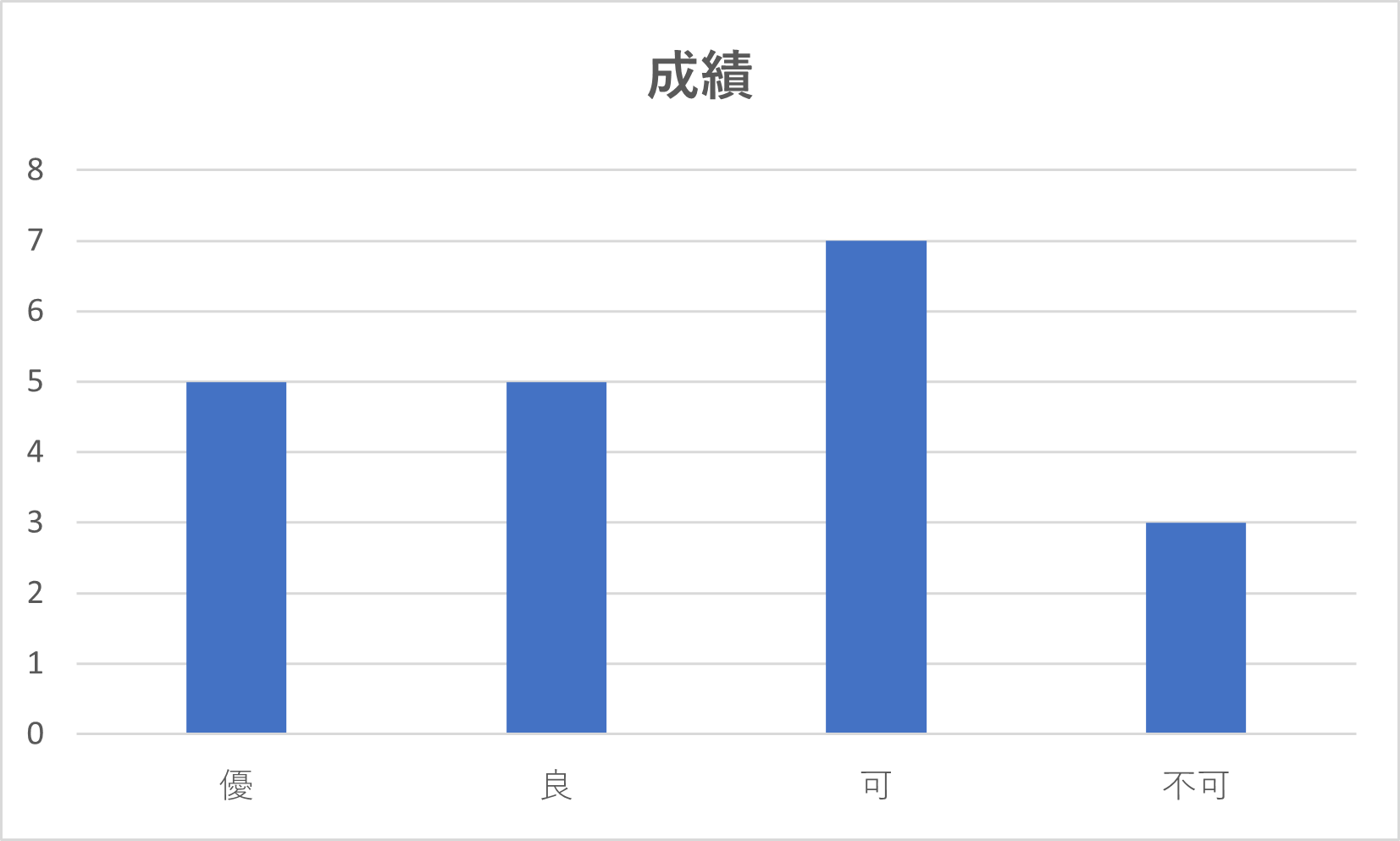
質的データの度数を表現するグラフとしては、棒グラフや円グラフなどがあげられます。
例1の度数表を棒グラフと円グラフで表すとそれぞれ次のようになる。
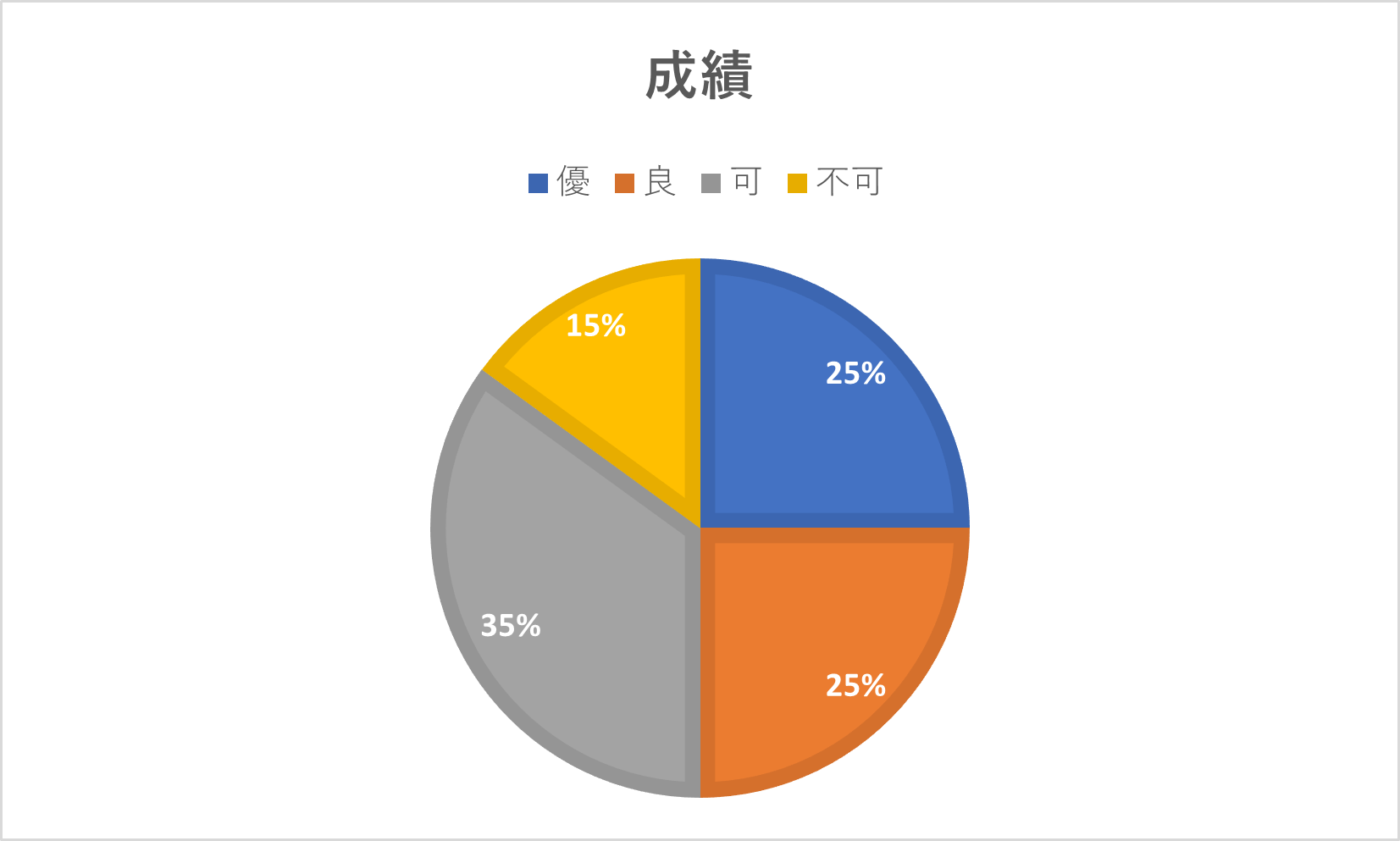
2変数データの記述
1つの個体に対して複数のデータがあるとき、それを多変数データという。
ここでは、2変数データに着目してそれらの間の関係(相関という)について記述することを考えます。
散布図と相関関係およびクロス集計表
個体 \( i \) に対して、2次元データ \( (x_i,y_i) \) があり、 \( x_i,y_i \) が量的データであるならば、横軸に \( x \) 、縦軸に \( y \) をとって2次元平面上に2次元データを配置することができます。
その図のことを散布図(相関図)といいます。
20人の数学と物理のテストの点に関して、散布図を作成すると次のようになる。
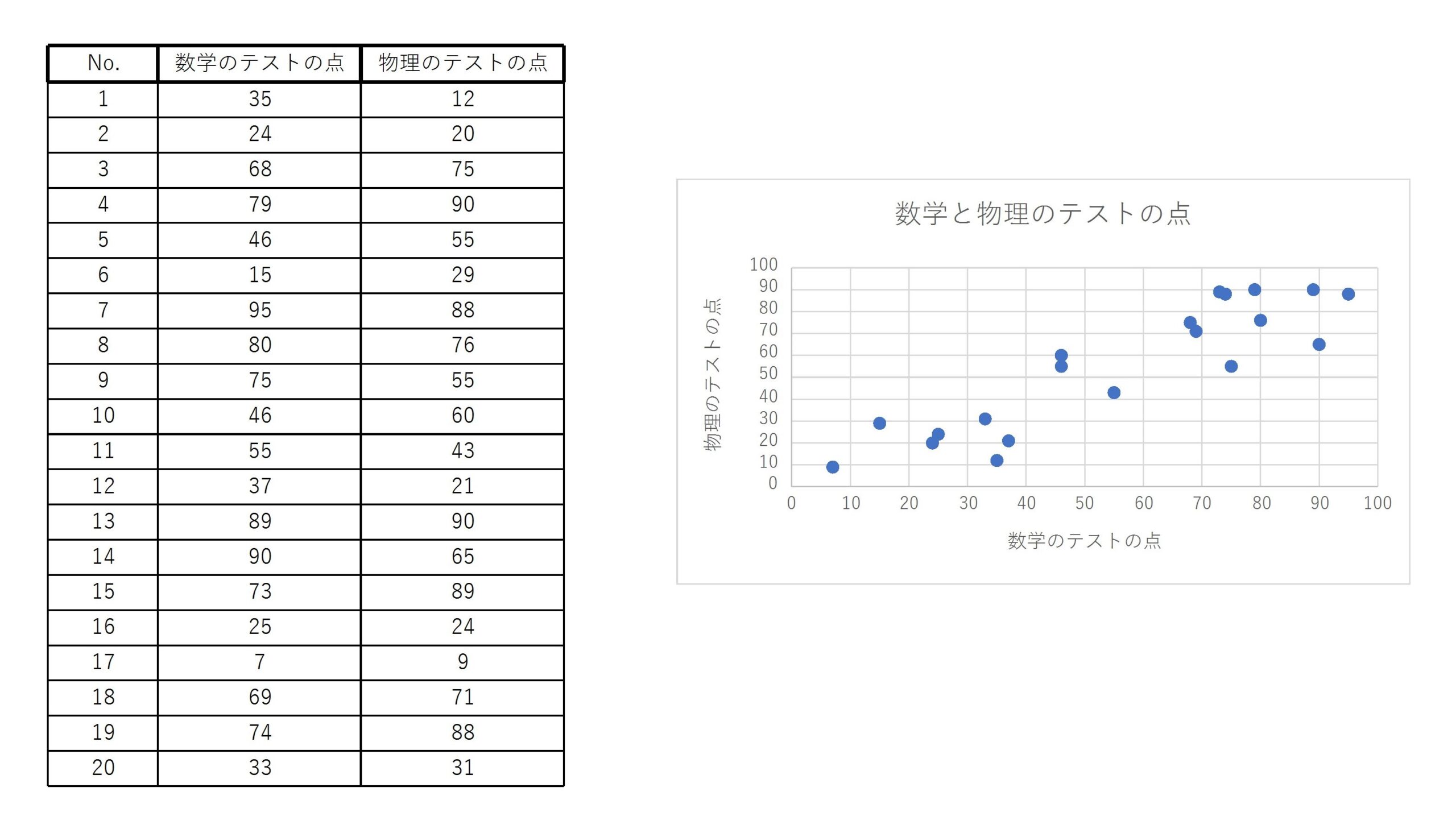
散布図の点の散らばり方によって、2変数データがどのような相関をしているかが分かります。
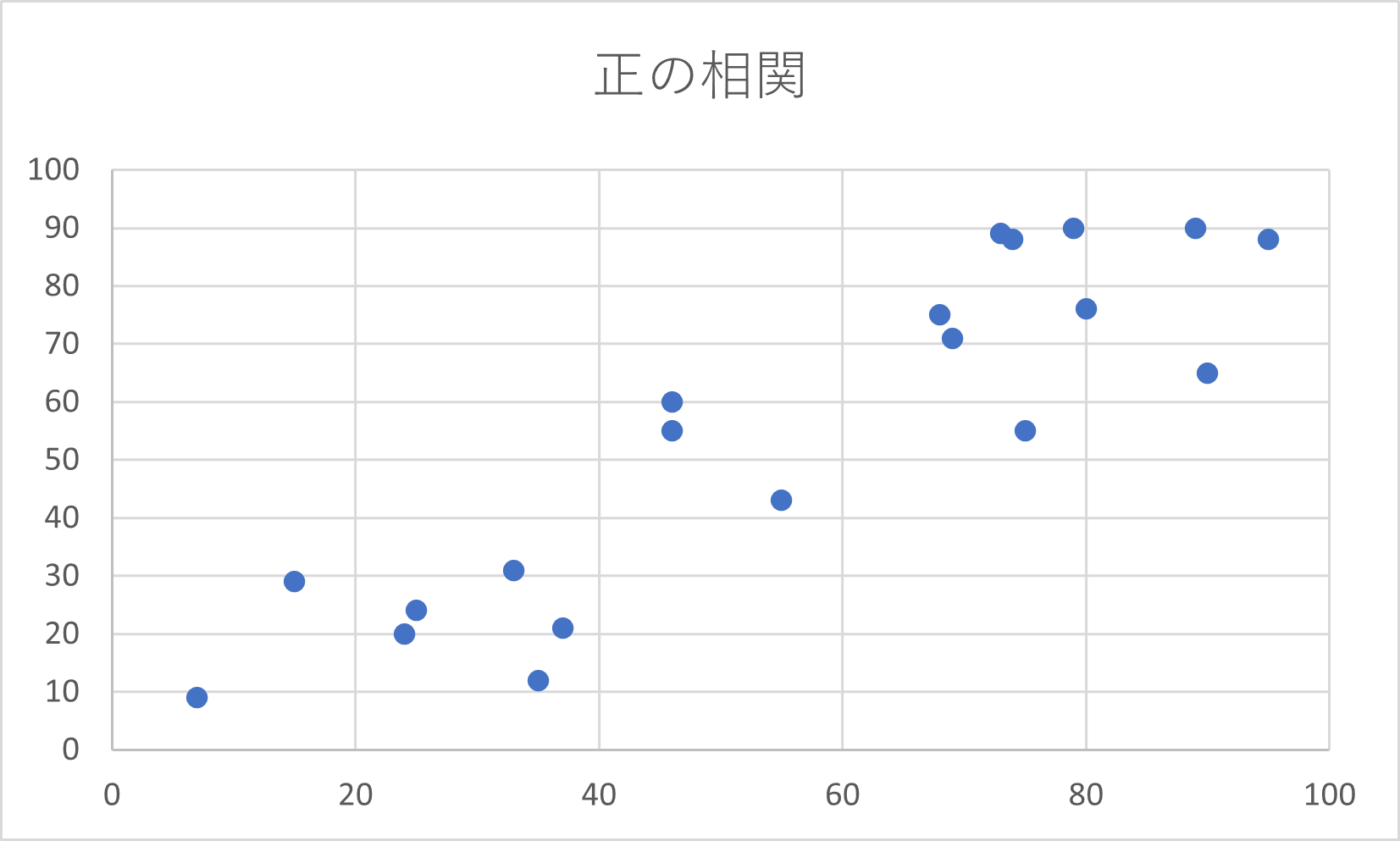
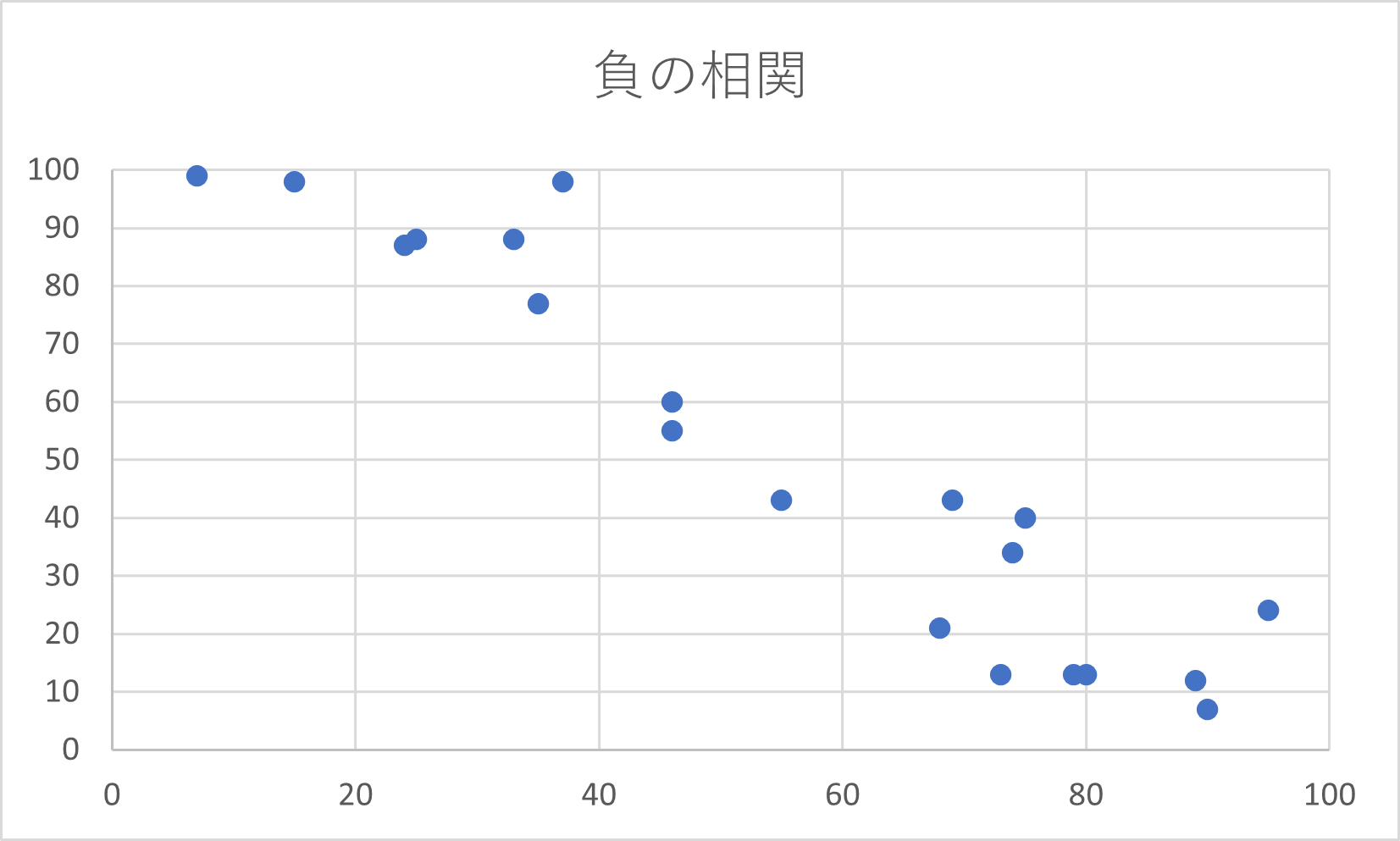
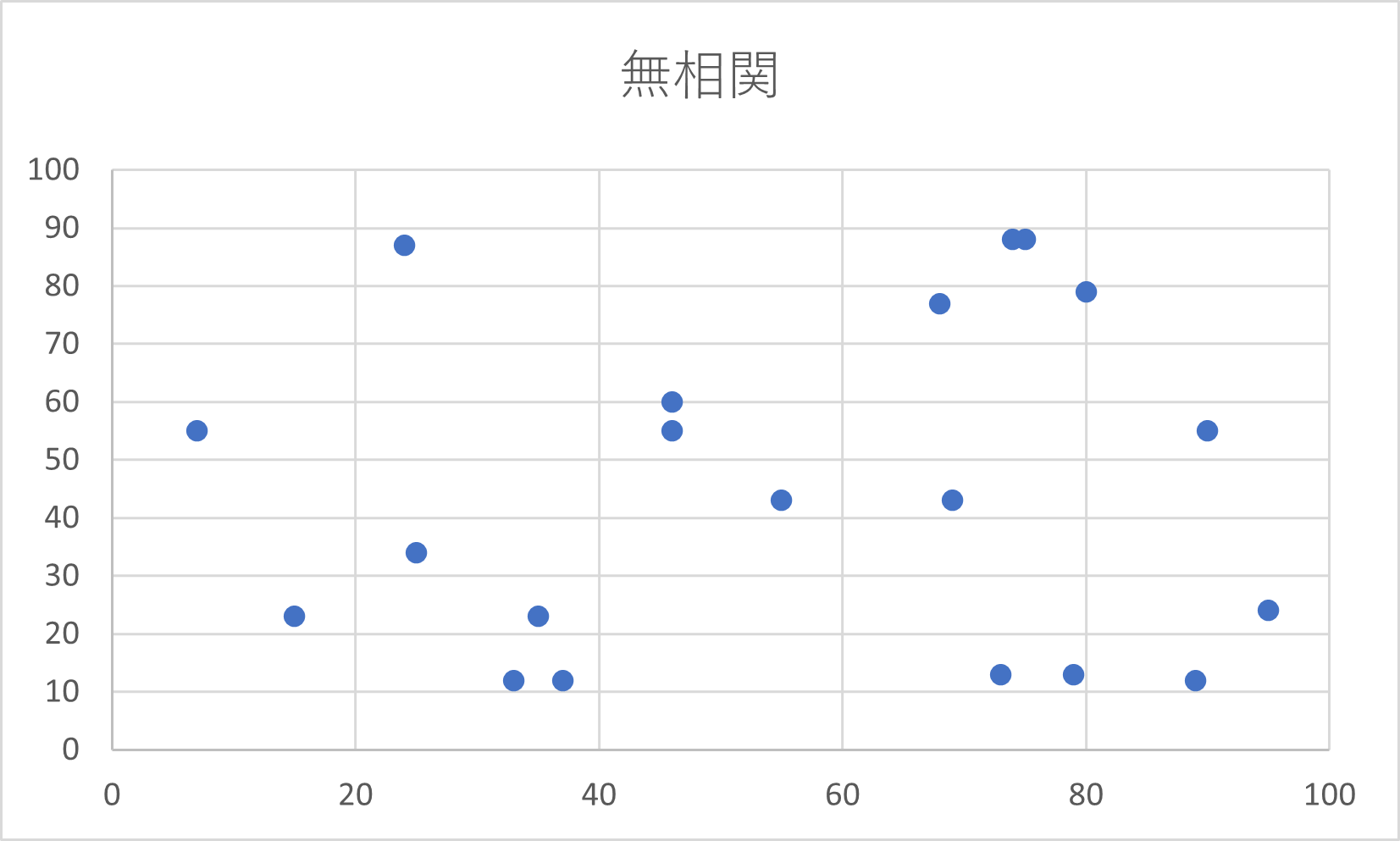
まとめると、
2つの変数の間の関係のことを相関関係という。
2つの変数の間に直線のような関係があるとき、相関関係があるという。
とくに、左下から右上にかけて点が散らばっているときに正の相関関係があるといい、左上から右下にかけて点が散らばっているときに負の相関関係があるという。
直線関係の度合いによって、強い相関関係や弱い相関関係があるともいう。
また、相関関係がないとき無相関であるという。
例3の散布図は強い正の相関があるといえる。
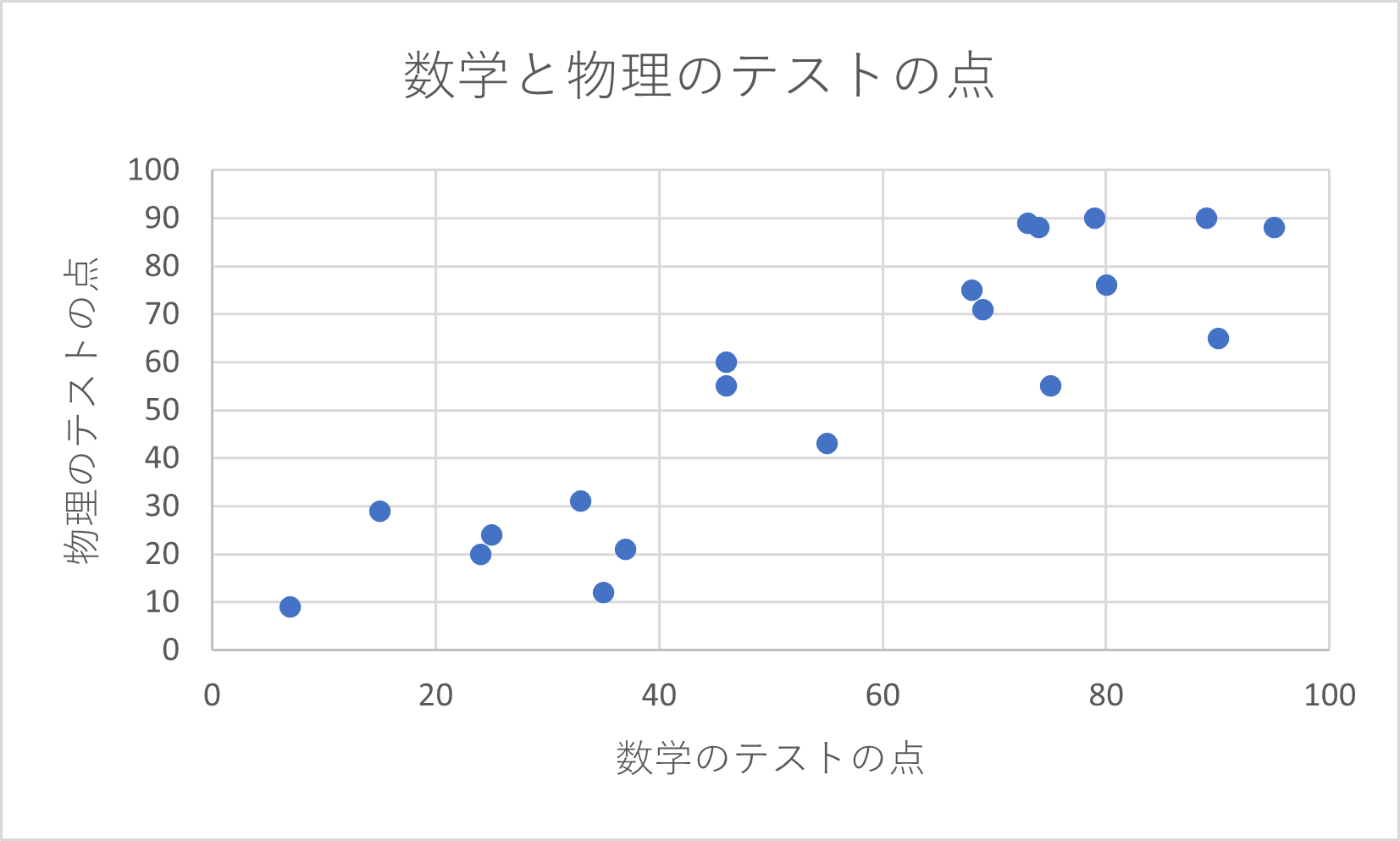
つまり、数学のテストの点が高い人は物理のテストの点も高い傾向があるということである。
では、2つの変数 \( x,y \) が片方もしくはともに質的データである場合はどうしたらよいのでしょうか。
そのときは、量的や質的によらないクロス集計表(分割表)を書くとよいです。
20人の家の間取りと賃貸の関係に関してクロス集計表を作成すると次のようになる。
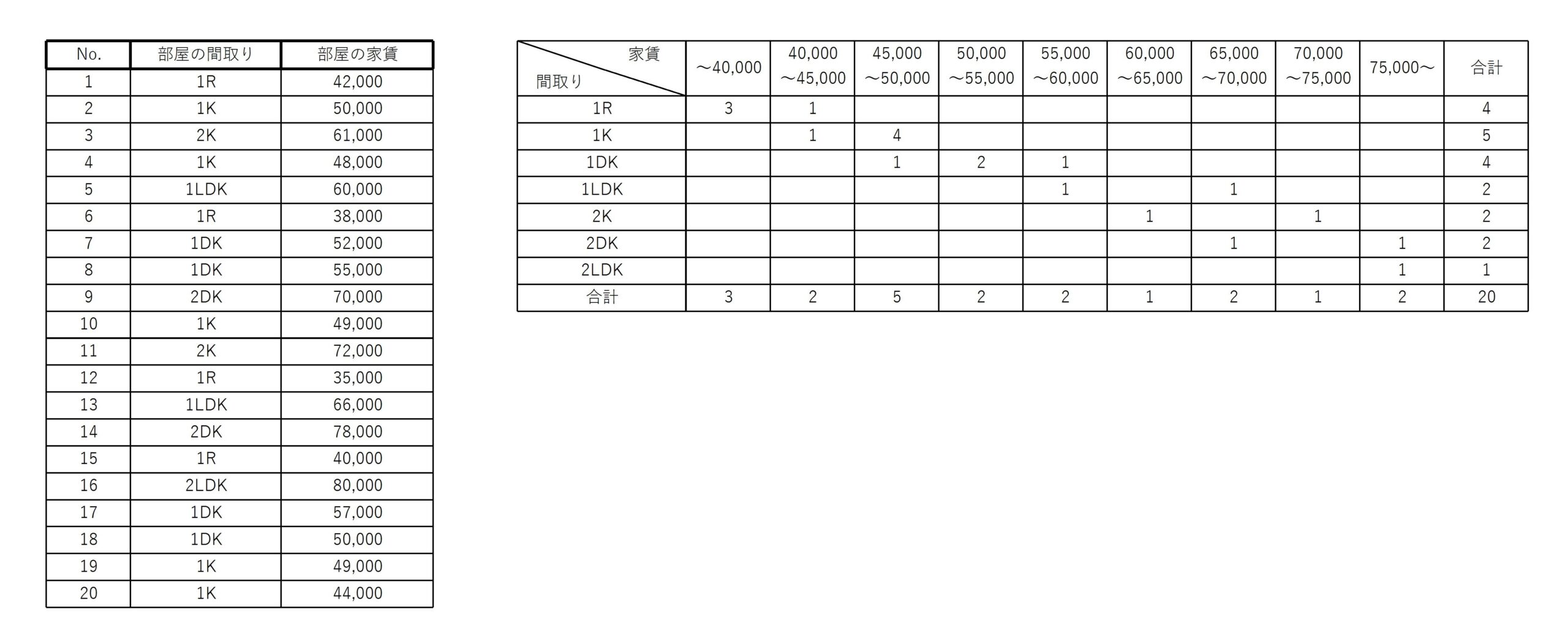
相関係数
2変数データの間の関係を図や表で見てきました。
これは視覚的にはわかりやすいですが、きちんとした関係を議論したいときには、やはりどの程度相関関係があるのかを数値的に出した方がよいです。
そこで、相関関係を数値的に表現した相関係数を考えます。
そのために、共分散を次で定義します。
\( n \) 個の2変数データ
$$ (x_1,y_1), \ (x_2,y_2), \ \cdots, \ (x_n,y_n) $$
に対して、共分散 \( s_{xy} \) を次で定義する。
$$ \begin{align} s_{xy}&=\frac{1}{n}\{ (x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y}) \} \\ &=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y}) \end{align} $$
ここで、 \( \bar{x},\bar{y} \) はそれぞれ \( x_1,x_2\cdots,x_n \) と \( y_1,y_2,\cdots,y_n \) の平均値である。
共分散は分散とは異なり、2変数データ \( (x_i,y_i) \) が平均値 \( (\bar{x},\bar{y}) \) と比べてどこに位置するかによって、正負の値をとります。
$$ (x_i-\bar{x})(y_i-\bar{y}) $$
が正となるのは
$$ (x_i-\bar{x})>0 \ かつ \ (y_i-\bar{y})>0 $$
もしくは
$$ (x_i-\bar{x})<0 \ かつ \ (y_i-\bar{y})<0 $$
のときになります。
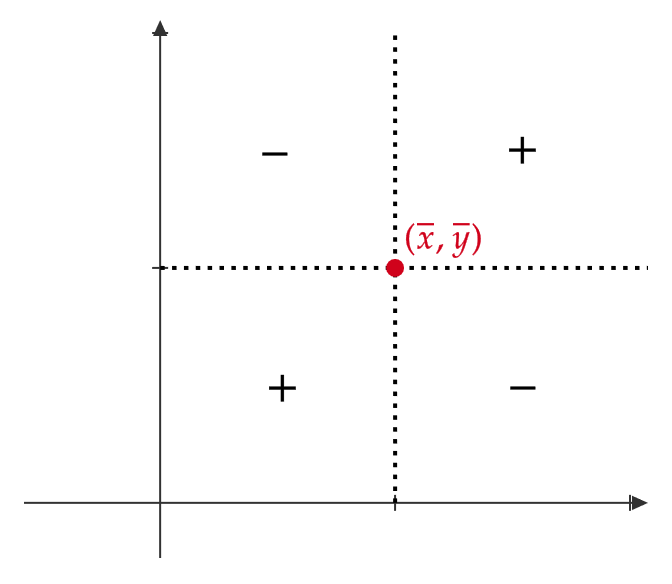
これはつまり、平均値 \( (\bar{x},\bar{y}) \) から見て左下もしくは右上に2変数データ \( (x_i,y_i) \) が位置するということになります。
同様にして、
$$ (x_i-\bar{x})(y_i-\bar{y}) $$
が負となるのは
$$ (x_i-\bar{x})>0 \ かつ \ (y_i-\bar{y})<0 $$
もしくは
$$ (x_i-\bar{x})<0 \ かつ \ (y_i-\bar{y})>0 $$
のときになります。
これはつまり、平均値 \( (\bar{x},\bar{y}) \) から見て左上もしくは右下に2変数データ \( (x_i,y_i) \) が位置するということになります。
この共分散をもとにして、相関係数を次で定義します。
\( n \) 個の2変数データ
$$ (x_1,y_1), \ (x_2,y_2), \ \cdots, \ (x_n,y_n) $$
に対して、 \( x \) 変数に関する標準偏差を \( s_x \) 、 \( y \) 変数に関する標準偏差を \( s_y \) 、共分散を \( s_{xy} \) とするとき、相関係数 \( r_{xy} \) を次で定める。
$$ r_{xy}=\frac{s_{xy}}{s_xs_y}=\frac{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2}\sqrt{\frac{1}{n}\sum_{i=1}^n(y_i-\bar{y})^2}} $$
相関係数は次が成り立ちます。
$$ -1≦r_{xy}≦1 $$
定理1の証明(気になる方だけクリックしてください)
任意の実数 \( t \) に対して、
$$ \begin{align} &\frac{1}{n}\sum_{i=1}^n\{ (x_i-\bar{x})t+(y_i-\bar{y})\}^2 \\ &=\frac{1}{n}\left\{ \sum_{i=1}^n(x_i-\bar{x})^2t^2+2\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})t+\sum_{i=1}^n(y_i-\bar{y})^2 \right\} \\ &=s_x^2t^2+2s_{xy}t+s_y^2 \end{align} $$
最左辺が \( ≧0 \) なので、
$$ s_x^2t^2+2s_{xy}t+s_y^2≧0 $$
したがって、2次方程式の判別式は
$$ D=4s_{xy}^2-4s_x^2s_y^2≦0 $$
となるので、
$$ r_{xy}^2=\frac{s_{xy}^2}{s_x^2s_y^2}≦1 $$
よって、 \( -1≦r_{xy}≦1 \) である。
先ほどの共分散の考察より、2変数データが正の相関があるときは \( r_{xy}>0 \) 、負の相関があるときは \( r_{xy}<0 \) となります。
目安としては、 \( n=20 \) ぐらいであれば \( r_{xy} \) が \( 0.9 \) ぐらいであれば強い正の相関、 \( r_{xy} \) が \( 0.7 \) ぐらいであれば弱い正の相関、 \( r_{xy} \) が \( 0.5 \) ほどでは相関関係があまり見られないです。
また、 \( |r_{xy}| \) が \( 1 \) に近いほどデータは1本の直線の近くに集中することになります。
例3の2変数データの相関係数を求める。

まず、 \( s_x,s_y,s_{xy} \) を求めると、
$$ s_x=26.23, \quad s_y=28.02, \quad s_{xy}=658.64 \quad (小数点第三位を四捨五入) $$
よって、
$$ r_{xy}=\frac{s_{xy}}{s_xs_y}=0.90 \quad (小数点第三位を四捨五入) $$
したがって、例4の結論と同じくこの2変数データは強い正の相関をもつ。
偏相関係数
相関係数は2つのデータの間の相関関係を数値で表すことのできる役に立つ指標であるが、注意が必要でもあります。
まず、次の例を見てみましょう。
20の市区町村の学校と銀行の数をまとめたデータの散布図と相関係数を求める。
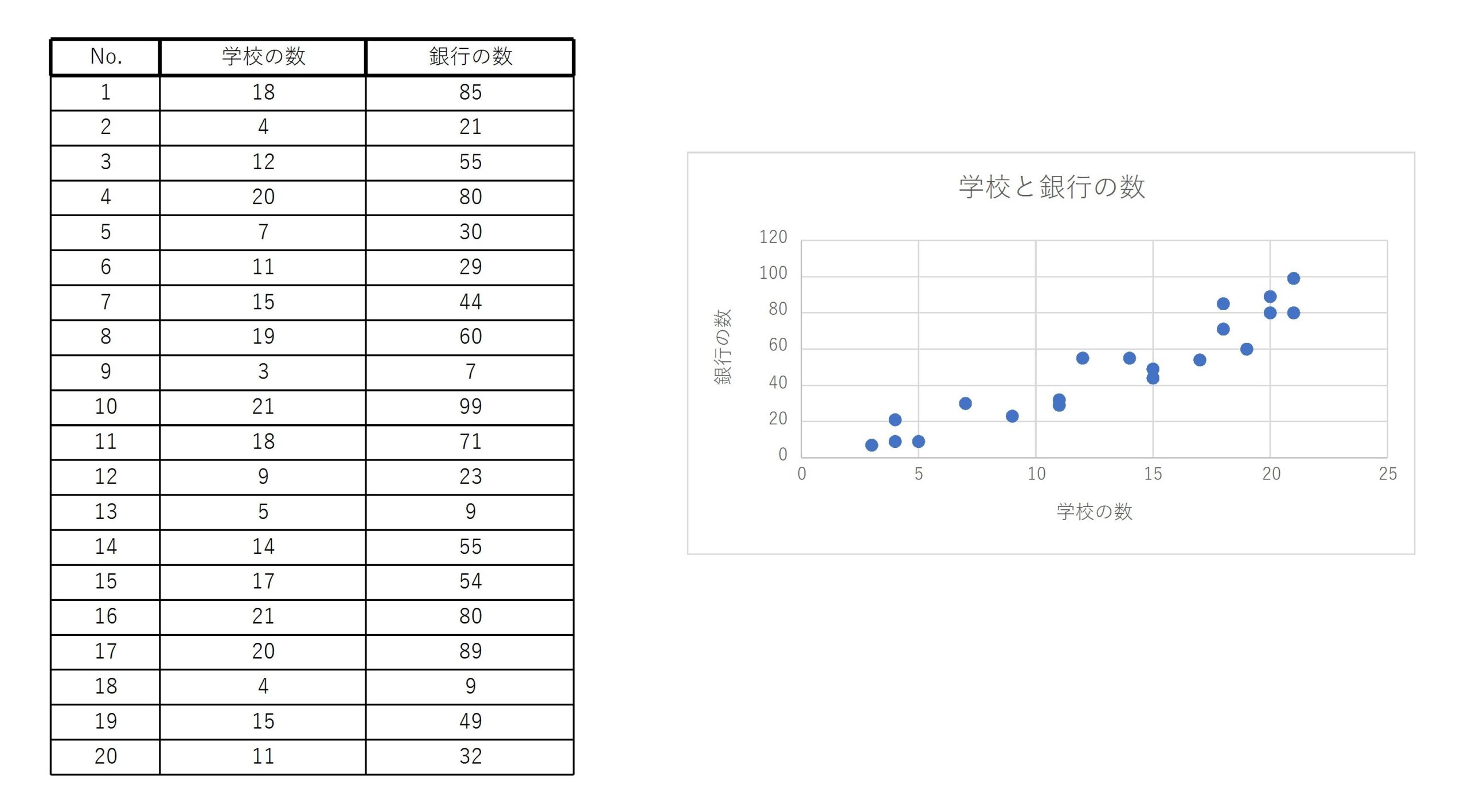
また、相関係数は
$$ r_{xy}=0.94 \quad (小数点第三位を四捨五入) $$
したがって、この2変数データは強い正の相関をもつ。
では、この例から学校が多いところは銀行が多いというようにいえるのでしょうか。
学校と銀行には関係があるようには思えないため、これはいえません。
では、なぜ強い正の相関をもったのでしょうか。
それは、学校が多い市区町村は人口が多い市区町村であり、人口が多い市区町村には銀行の数も多くなる、というように、間に人口が多いという見えない情報が挟まっているからです。
つまり、学校の数と人口、人口と銀行の数が関係をもっているため、関係がない学校の数と銀行の数の間に正の相関関係が出てきたということになります。
これを見かけ上の相関(擬相関)といいます。
その見かけ上の相関を調べる方法として、偏相関係数を求める方法があります。
3つの変数 \( x,y,z \) に対して、変数 \( x \) の影響を除いた後の変数 \( y \) と変数 \( z \) の間の相関係数を偏相関係数といい、 \( r_{yz\cdot x} \) と表す。これは次のように与えられる。
$$ r_{yz\cdot x}=\frac{r_{yz}-r_{xy}r_{xz}}{\sqrt{1-r^2_{xy}}\sqrt{1-r^2_{xz}}} $$
ここで、 \( r_{xy} \) は変数 \( x \) と \( y \) の相関係数である。
例7のデータに人口のデータを付けたものを考える。
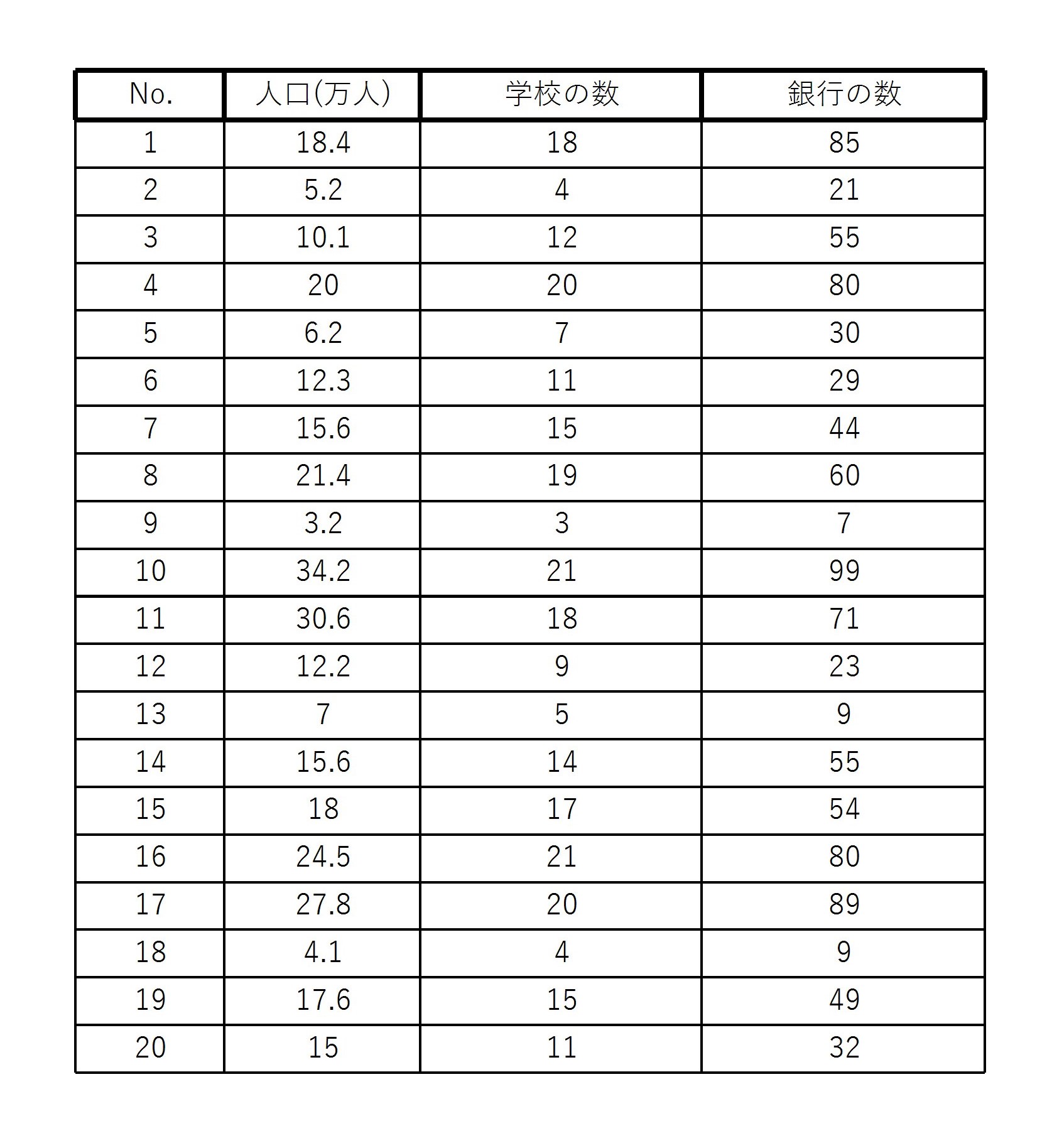
このとき、人口(変数 \( x \) )の影響を除いた後の学校の数(変数 \( y \) )と銀行の数(変数 \( z \) )の間の相関係数(偏相関係数)を求める。
$$ r_{xy}=0.91, \quad r_{xz}=0.89, \quad r_{yz}=0.94 \quad (小数点第三位を四捨五入) $$
より、偏相関係数 \( r_{yz\cdot x} \) は、
$$ r_{yz\cdot x}=\frac{r_{yz}-r_{xy}r_{xz}}{\sqrt{1-r^2_{xy}}\sqrt{1-r^2_{xz}}}=0.69 \quad (小数点第三位を四捨五入) $$
よって、人口の影響を除けば、学校の数と銀行の数との相関はあまり強くないことがいえる。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

