こんにちは、ひかりです。
今回は微分積分学から多変数関数の極大値・極小値について解説していきます。
この記事では以下のことを紹介します。
- 1変数関数の極大値・極小値について
- 2変数関数の極大値・極小値と停留店・鞍点について
1変数関数の極大値・極小値
多変数関数の前にまずは1変数関数の極大値・極小値について簡単に解説していきます。
詳しくは以下の記事をご覧ください。
まず、1変数関数の極大値・極小値は次のように定義されていました。
関数 \( f(x) \) が \( x=a \) の近くで定義されていて、 \( x=a \) の十分近くでは \( x=a \) を除いて \( f(x)<f(a) \) となるとき、 \( f(x) \) は \( x=a \) において極大になるといい、 \( f(a) \) を極大値とよぶ。
同様に、 \( x=a \) の十分近くでは \( x=a \) を除いて \( f(x)>f(a) \) となるとき、 \( f(x) \) は \( x=a \) において極小になるといい、 \( f(a) \) を極小値とよぶ。
さらに、極大値と極小値を合わせて極値という。
ここで、高校数学(または高校数学(数学Ⅲ)10の記事)にて勉強した内容について、きちんと定理の形で述べて証明を与えてみましょう。
関数 \( f(x) \) が \( x=a \) において微分可能であり、かつ \( x=a \) において極値をとるならば、 \( f'(a)=0 \)
定理1の証明(気になる方だけクリックしてください)
\( f(x) \) が \( x=a \) で極大であるとします。
このとき、 \( f(x) \) を \( x=a \) のある近傍 \( I \) 上に制限して考えると、 \( f(a) \) は最大値となります。
すると、 \( x\in I \) 上で \( f(x)-f(a)≦ 0 \) であるので、 \( \frac{f(x)-f(a)}{x-a} \) は
$$ \begin{cases} \frac{f(x)-f(a)}{x-a}≧0 & (x<aのとき) \\ \frac{f(x)-f(a)}{x-a}≦0 & (x>aのとき) \end{cases} $$
となります。
よって、それぞれ \( x\to a-0, \ x\to a+0 \) とすることにより、 \( f'(a)≧0 \) かつ \( f'(a)≦0 \) となります。
したがって、 \( f'(a)=0 \) となります。極小の場合も同様に示せます。
関数 \( y=f(x) \) は \( x=a \) で連続であるとして、十分小さな \( h>0 \) をとる。
このとき、 \( a-h<x<a \) において \( f'(x)>0 \ (f'(x)<0) \) であり、 \( a<x<a+h \) において \( f'(x)<0 \ (f'(x)>0) \) であるとき、 \( f(x) \) は \( x=a \) において極大 (極小) である。
定理2の証明(気になる方だけクリックしてください)
\( f(x) \) が \( x=a \) において極大となる方の主張を示します。
まず、 \( a-h<x<a \) とします。このとき、 \( f \) に \( [x,a] \) 上で平均値の定理を用いると、
$$ f(a)-f(x)=f'(c)(a-x) \quad (x<c<a) $$
となる \( c \) が存在します。よって、定理の仮定から \( f'(c)>0 \) であるので、
$$ f(a)-f(x)>0 $$
次に、 \( a<x<a+h \) として、 \( f \) に \( [a,x] \) 上で平均値の定理を用いると、
$$ f(x)-f(a)=f'(d)(x-a) \quad (a<d<x) $$
となる \( d \) が存在します。よって、定理の仮定から \( f'(d)<0 \) であるので、
$$ f(x)-f(a)<0 $$
よって、 \( f(x) \) は \( x=a \) において極大となります。
極小の方についても同様に示せます。
関数 \( y=f(x) \) が \( x=a \) で \( C^2 \) 級で \( f'(a)=0 \) のとき、 \( f^{\prime\prime}(a)>0 \) ならば \( x=a \) で極小となり、 \( f^{\prime\prime}(a)<0 \) ならば \( x=a \) で極大となる。
定理3の証明(気になる方だけクリックしてください)
\( f^{\prime\prime}(a)>0 \) ならば \( x=a \) で極小となることを示します。
\( y=f(x) \) が \( x=a \) で \( C^2 \) 級より、 \( f^{\prime\prime}(x) \) は連続であるので、 \( x=a \) の十分近くでは \( f^{\prime\prime}(x)>0 \) となります。
\( [a,x] \) または \( [x,a] \) において、 \( f \) にテイラーの定理を用いると、定理の仮定より \( f'(a)=0 \) であるので、
$$ f(x)=f(a)+f'(a)(x-a)+R_2=f(a)+\frac{1}{2!}f^{\prime\prime}(c)(x-a)^2 $$
となる \( c \) が \( a \) と \( x \) の間に存在します。
このとき、
$$ f^{\prime\prime}(c)>0 \ (証明の2文目より), \quad (x-a)^2>0 $$
より、
$$ f(x)-f(a)>0 $$
よって、 \( f(x) \) は \( x=a \) で極小となります。
極大の場合も同様に示せます。
(1) \( f(x)=2x^3-3x^2-12x+3 \) の極大値・極小値を求める。
$$ f'(x)=6x^2-6x-12=6(x+1)(x-2), \quad f^{\prime\prime}(x)=12x-6 $$
であるので、増減表を書くと次のようになる。
| \( x \) | \( \cdots \) | \( -1 \) | \( \cdots \) | \( \frac{1}{2} \) | \( \cdots \) | \( 2 \) | \( \cdots \) |
| \( f^{\prime\prime}(x) \) | \( – \) | \( – \) | \( – \) | \( 0 \) | \( + \) | \( + \) | \( + \) |
| \( f'(x) \) | \( + \) | \( 0 \) | \( – \) | \( – \) | \( – \) | \( 0 \) | \( + \) |
| \( f(x) \) | \( \nearrow \) | \( 10 \) | \( \searrow \) | \( \searrow \) | \( \searrow \) | \( -17 \) | \( \nearrow \) |
よって、 \( f(x) \) は \( x=-1 \) のとき極大値 \( 10 \) をとり、 \( x=2 \) のとき極小値 \( -17 \) をとる。
(2) 次の関数を考える。
$$ f(x)=\begin{cases} x^2+\frac{x^2}{2}\sin\frac{1}{x} & (x\not=0 のとき) \\ 0 & (x=0 のとき) \end{cases} $$
まず、この関数が \( x=0 \) で極小であることを示す。
\( x\not=0 \) に対して、 \( \sin\frac{1}{x}≧-1 \) より、
$$ f(x)≧x^2-\frac{x^2}{2}=\frac{x^2}{2}>0 $$
よって、 \( f(0)=0 \) より、 \( f(x) \) は \( x=0 \) で極小となる。
しかし、このとき \( x=0 \) の近くでの \( f'(x) \) の符号を見てみると、
$$ f'(x)=2x+x\sin\frac{1}{x}-\frac{1}{2}\cos\frac{1}{x} \quad (x\not=0) $$
より、 \( x\to 0 \) とすると、
$$ 2x+x\sin \frac{1}{x}\to 0 \quad \frac{1}{2}\cos \frac{1}{x} は \ -1 \ から \ 1 \ の間を細かく振動する $$
であるので、 \( f'(x) \) の符号は \( x=0 \) の近くで細かく変化する。
よって、定理2の逆は成り立たない。
2変数関数の極大値・極小値と停留点・鞍点
2変数関数の極大値・極小値
定義1と同様にして、2変数関数の極大値・極小値を次で定めます。
関数 \( f(x,y) \) が点 \( (x,y)=(a,b) \) の近くで定義されていて、 \( (x,y)=(a,b) \) の十分近くでは \( f(x,y)≦f(a,b) \) となるとき、 \( f(x,y) \) は \( (x,y)=(a,b) \) において広義の極大になるといい、 \( f(a,b) \) を広義の極大値とよぶ。
とくに、 \( (x,y)\not=(a,b) \) では \( f(x,y)<f(a,b) \) となるとき、 \( f \) は \( (x,y)=(a,b) \) において極大になるといい、 \( f(a,b) \) を極大値とよぶ。
同様に、 \( (x,y)=(a,b) \) の十分近くでは \( f(x,y)≧f(a,b) \) となるとき、 \( f(x,y) \) は \( (x,y)=(a,b) \) において広義の極小になるといい、 \( f(a,b) \) を広義の極小値とよぶ。
とくに、 \( (x,y)\not=(a,b) \) では \( f(x,y)>f(a,b) \) となるとき、 \( f \) は \( (x,y)=(a,b) \) において極小になるといい、 \( f(a,b) \) を極小値とよぶ。
さらに、広義の極大値と広義の極小値を合わせて広義の極値といい、極大値と極小値を合わせて極値という。
定理1と似たような定理が成り立ちます。証明は定理1と同様です。
関数 \( f(x,y) \) が \( (x,y)=(a,b) \) において偏微分可能であり、かつ \( (x,y)=(a,b) \) において広義の極値をとるならば、 \( f_x(a,b)=f_y(a,b)=0 \)
\( f(x,y)=xy \) を考える。
$$ f_x(0,0)=f_y(0,0)=0 $$
であり、 \( f(0,0)=0 \) となるが、 \( (0,0) \) の近くで \( f(x,y)=xy \) は正にも負にもなるので、 \( f(0,0) \) は広義の極値ではない。
よって、定理4の逆は成り立たない。
2変数関数の停留点・鞍点
まず、停留点を定義します。
関数 \( f(x,y) \) に対して、 \( f_x(a,b)=f_y(a,b)=0 \) となる点 \( (a,b) \) を \( f \) の停留点という。
定理4より、偏微分可能で点 \( (a,b) \) で広義の極値をとるならば点 \( (a,b) \) は停留点となります。
対偶をとると、停留点でない点は広義の極値にはなりえないということがわかります。
よって、停留点は広義の極値の候補を与えます。
しかし、定理4の逆は成り立たないので、停留点であっても広義の極値とならない場合もあります。
\( f(x,y)=x^2-y^2 \) を考える。
$$ f_x(0,0)=f_y(0,0)=0 $$
より、原点 \( (0,0) \) は停留点となる。
しかし、 \( f(x,0)=x^2 \) を考えると \( x=0 \) で極小になり、 \( f(0,y)=-y^2 \) を考えると \( y=0 \) で極大となる。
よって、 \( f(0,0) \) は極大値でも極小値でもない。
この例のような停留点のことを鞍点(あんてん)といいます。つまり、
極大となる方向と極小となる方向をもつ停留点を鞍点という。
なぜ「鞍点」とよばれるのでしょうか。
先ほどの例3の関数のグラフを考えてみましょう。
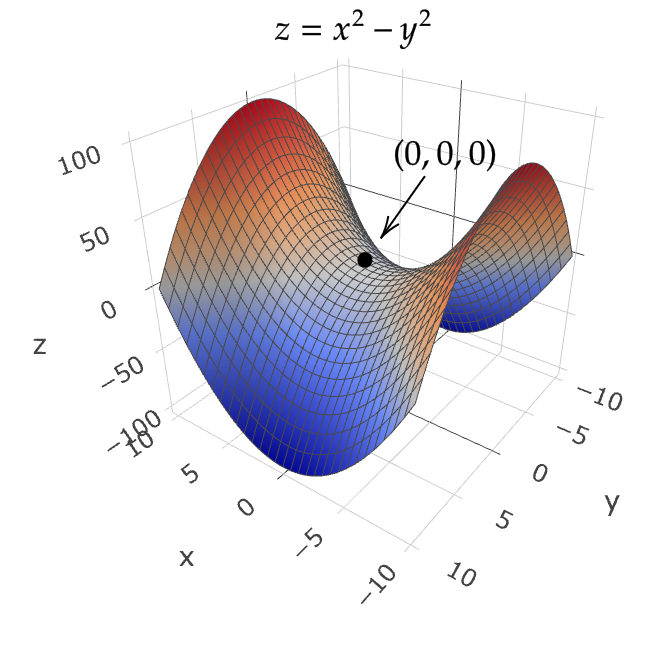
すると、点 \( f(0,0)=(0,0,0) \) は \( x \) 軸方向には下に凸、 \( y \) 軸方向には上に凸のような形をしています。
これが馬の鞍(くら)の形をしていることから「鞍点」といわれていて、これは2つ以上の方向をもつ多変数関数ならではの概念となっています。
またこの場合極大値・極小値とならないことはグラフからも読み取れます。
最後に、2変数関数の極値の判別方法について紹介します。
\( f=f(x,y) \) は点 \( (a,b) \) の近くで \( C^2 \) 級で
$$ f_x(a,b)=f_y(a,b)=0 $$
とする。このとき、
$$ D=f_{xy}^2-f_{xx}f_{yy} $$
とおくと、次のように極値を判別することができる。
(1) \( D>0 \) のとき、 \( f(a,b) \) は鞍点であり、極値ではない。
(2) \( D<0, \ f_{xx}(a,b)>0 \) のとき、 \( f(a,b) \) は極小値である。
(3) \( D<0, \ f_{xx}(a,b)<0 \) のとき、 \( f(a,b) \) は極大値である。
(4) \( D=0 \) のとき、 \( f(a,b) \) は極値であるか判定できない。
定理5の証明(気になる方だけクリックしてください)
\( f_x(a,b)=f_y(a,b)=0 \) に注意して2変数関数のテイラーの定理を用いると、
$$ \begin{align} f(a+h,b+k)-f(a,b)&=hf_x(a,b)+kf_y(a,b)+R_2=R_2 \\ &=\frac{1}{2}(f_{xx}(c,d)h^2+2f_{xy}(c,d)hk+f_{yy}(c,d)k^2) \end{align} $$
をみたす \( c \) が \( a \) と \( x \) の間に、 \( d \) が \( y \) と \( b \) の間に存在します。
ここで、 \( f_{xx},f_{xy},f_{yy} \) の連続性より、 \( (h,k)\to (0,0) \) とすると、 \( (c,d)\to (a,b) \) より、
$$ f_{xx}(c,d)\to f_{xx}(a,b), \quad f_{xy}(c,d)\to f_{xy}(a,b), \quad f_{yy}(c,d)\to f_{yy}(a,b) \ ((h,k)\to (0,0)) $$
よって、 \( (h,k) \) が十分 \( (0,0) \) に近いとき、 \( f(a+h,b+k)-f(a,b) \) の符号は
$$ Q(h,k)=f_{xx}(a,b)h^2+2f_{xy}(a,b)hk+f_{yy}(a,b)k^2 $$
の符号で決まります。
\( (h,k)\not=(0,0) \) のとき \( h\not=0 \) または \( k\not=0 \) となるので、ここでは \( k\not=0 \) とします。( \( h\not=0 \) の場合も同様)
\( Q(h,k) \) を \( k^2 \) で割ると、
$$ \begin{align} \frac{Q(h,k)}{k^2}&=f_{xx}(a,b)\left(\frac{h}{k} \right)^2+2f_{xy}(a,b)\frac{h}{k}+f_{yy}(a,b) \\ &=f_{xx}(a,b)X^2+2f_{xy}(a,b)X+f_{yy}(a,b) \end{align} $$
ここで、 \( \frac{h}{k}=X \) とおいています。
よって、次の2次方程式
$$ f_{xx}(a,b)X^2+2f_{xy}(a,b)X+f_{yy}(a,b)=0 \tag{1} $$
を調べれば、 \( f(a+h,b+k)-f(a,b) \) の符号がわかります。この2次方程式の判別式は
$$ D=f_{xy}^2-f_{xx}f_{yy} $$
となります。
(1) \( D>0 \) であれば、式(1)は2つの異なる実数解をもちます。つまり、 \( f(a+h,b+k)-f(a,b) \) は定符号ではないので、極値をもたず、さらに鞍点となる。
(鞍点になる理由はこの状況下では必ず \( f(x,y) \) が点 \( (a,b) \) の近くで双曲放物面(断面図が双曲線)となるからですが、詳細は省略します)
(2) \( D<0, f_{xx}(a,b)>0 \) であれば、式(1)は実数解をもちません。つまり、 \( f(a+h,b+k)-f(a,b) \) は定符号であり、 \( f_{xx}(a,b)>0 \) より、常に正となります。
よって、点 \( (a,b) \) で極小となり、 \( f(a,b) \) は極小値となります。
(3) \( D<0, f_{xx}(a,b)>0 \) であれば、\( f(a+h,b+k)-f(a,b) \) は常に負となります。
よって、点 \( (a,b) \) で極大となり、 \( f(a,b) \) は極大値となります。
(4) \( D=0 \) のときは極値かどうか判定できないことを具体例をだして示します。
次の3つの関数を考えます。
$$ f(x,y)=x^4+y^4, \quad g(x,y)=x^4-y^4, \quad h(x,y)=x^4-y^3 $$
これらの関数は原点 \( (0,0) \) で \( D=0 \) となるが、グラフを見ると、 \( f \) は極値をもち、 \( g \) は鞍点であり、 \( h \) は鞍点でも極値でもないです。
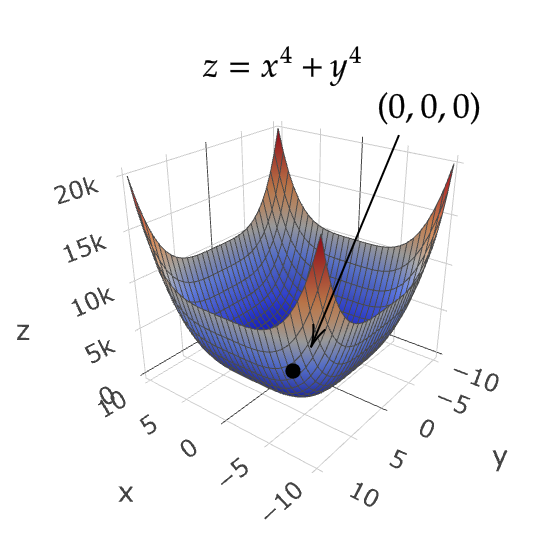
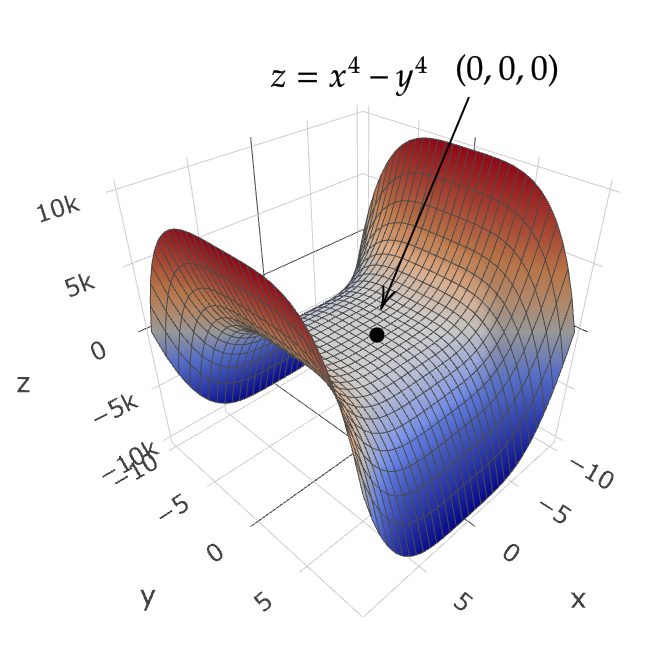
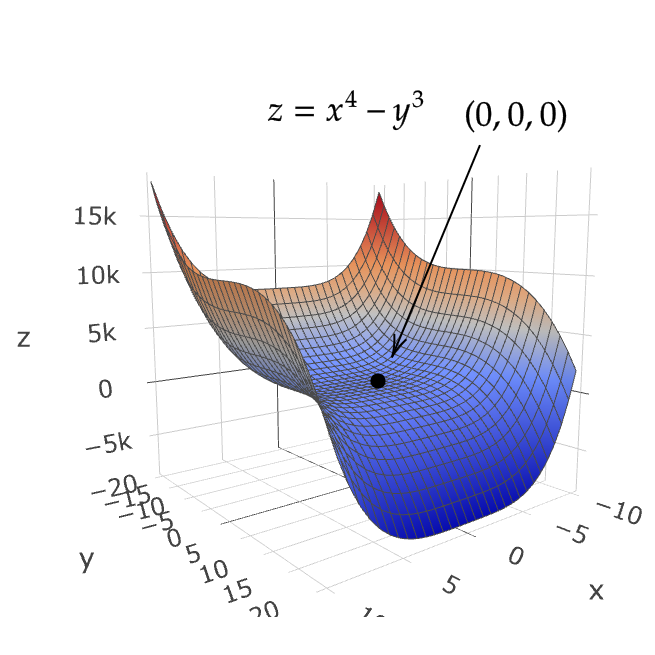
よって、 \( D=0 \) だけでは極値かどうかは判定できない。
\( f(x,y)=x^4+6x^2-8xy+2y^2 \) の極値を求める。
$$ f_x=4x^3+12x-8y=4(x^3+3x-2y) $$
$$ f_y=-8x+4y=4(-2x+y) $$
$$ f_{xx}=12x^2+12=12(x^2+1), \quad f_{xy}=-8, \quad f_{yy}=4 $$
となる。 \( f_x=f_y=0 \) となる点 \( (x,y) \) を求める。
\( f_y=0 \) より、 \( y=2x \)
\( f_x=0 \) より、 \( x^3+3x-2y=0 \)
これに、 \( y=2x \) を代入すると、
$$ x^3+3x-4x=x^3-x=x(x+1)(x-1)=0 $$
となるので、 \( x=0, \ \pm 1 \)
したがって、 \( (x,y)=(0,0),(-1,-2),(1,2) \) である。
これらの点の \( D=f_{xy}^2-f_{xx}f_{yy} \) を調べると、次のような表になる。
| \( (x,y) \) | \( f_{xx} \) | \( f_{yy} \) | \( f_{xy} \) | \( D \) | 判定 |
| \( (0,0) \) | \( 12 \) | \( 4 \) | \( -8 \) | \( 16 \) | \( D>0 \) |
| \( (-1,-2) \) | \( 24 \) | \( 4 \) | \( -8 \) | \( -32 \) | \( D<0, f_{xx}>0 \) |
| \( (1,2) \) | \( 24 \) | \( 4 \) | \( -8 \) | \( -32 \) | \( D<0, f_{xx}>0 \) |
よって、点 \( (0,0) \) は鞍点であり極値ではない、点 \( (-1,-2),(1,2) \) は極小である。
そのときの極小値は \( f(-1,-2)=f(1,2)=-1 \)
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

