こんにちは、ひかりです。
今回は微分積分学から広義積分とベータ関数・ガンマ関数について解説していきます。
この記事では以下のことを紹介します。
- 広義積分について
- 広義積分の収束判定について
- ベータ関数・ガンマ関数について
広義積分
関数 \( y=\log x \) を区間 \( [0,1] \) で積分することを考えてみましょう。
グラフからわかるように、 \( y=\log x \) は \( x=0 \) に近づくほど値が小さくなり、 \( x=0 \) そのものでは関数が定義されません。
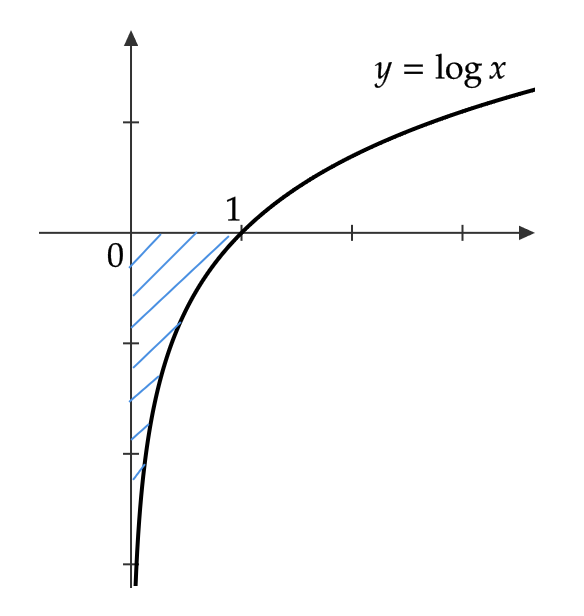
よって、普通に積分しようと思うと、
$$ \int_0^1\log xdx=[x\log x-x]^1_0=(1\log1-1)-(0\log 0-0)=-1-0\log 0 $$
となり、 \( 0\log 0\) が計算できません。
そこで、正の十分小さい定数 \( \varepsilon \) をとり、 \( y=\log x \) を区間 \( [\varepsilon,1] \) で積分してから、 \( \varepsilon\to +0 \) とすることを考えます。
すると、
$$ \begin{align} \int_0^1\log xdx&=\lim_{\varepsilon\to+0}\int_{\varepsilon}^1\log xdx=\lim_{\varepsilon\to +0}[x\log x-x]^1_{\varepsilon}=(1\log 1-1)-\lim_{\varepsilon\to+0}(\varepsilon\log \varepsilon-\varepsilon) \\ &=-1-\lim_{\varepsilon\to+0}\varepsilon\log \varepsilon \end{align} $$
ここで、
$$ \begin{align} \lim_{\varepsilon\to+0}\varepsilon\log \varepsilon&=-\lim_{\varepsilon\to+0}\frac{-\log \varepsilon}{\frac{1}{\varepsilon}} \\ &=-\lim_{\varepsilon\to+0}\frac{(-\log \varepsilon)’}{(\frac{1}{\varepsilon})’} \quad (\frac{\infty}{\infty}の不定形におけるロピタルの定理) \\ &=-\lim_{\varepsilon\to+0}\frac{-\frac{1}{\varepsilon}}{-\frac{1}{\varepsilon^2}}=-\lim_{\varepsilon\to+0}\varepsilon=0 \end{align} $$
よって、
$$ \int_0^1\log xdx=-1-\lim_{\varepsilon\to+0}\varepsilon\log \varepsilon=-1 $$
となり、積分が求められます。
上記のように有限の極限値が存在することにより求められる積分のことを広義積分という。
また、有限な極限値が存在するとき、広義積分は収束するといい、収束しないとき発散するという。
さらに、関数 \( f(x) \) が無限区間 \( [a,\infty) \) で連続であり、極限値 \( \displaystyle \lim_{b\to\infty}\int_a^bf(x)dx \) が存在して有限であるとき、この極限値を \( \displaystyle \int_a^{\infty}f(x)dx \) と表す。
同様に、
$$ \lim_{a\to-\infty}\int_a^bf(x)dx, \quad \lim_{a\to-\infty, \ b\to \infty}\int_a^bf(x)dx $$
が存在して有限のとき、それらをそれぞれ
$$ \int_{-\infty}^bf(x)dx, \quad \int^{\infty}_{-\infty}f(x)dx $$
と表す。
(1) 実数 \( \alpha \) に対して、 \( \displaystyle \int_0^1\frac{1}{x^{\alpha}}dx \) を求める。
\( \frac{1}{x} \) は \( x=0 \) で定義されないことに注意する。
\( \alpha=1 \) のときは、
$$ \int_0^1\frac{1}{x}dx=\lim_{\varepsilon\to+0}\int_{\varepsilon}^1\frac{1}{x}dx=\lim_{\varepsilon\to+0}\left[ \log x\right]^1_{\varepsilon}=-\lim_{\varepsilon\to+0}\log \varepsilon=\infty $$
であるので、この広義積分は発散する。
\( \alpha\not=1 \) のときは、
$$ \begin{align} \int_0^1\frac{1}{x^{\alpha}}dx&=\lim_{\varepsilon\to+0}\int_{\varepsilon}^1\frac{1}{x^{\alpha}}dx=\frac{1}{1-\alpha}\cdot \lim_{\varepsilon\to+0}\left[ x^{1-\alpha} \right]^1_{\varepsilon} \\ &=\frac{1}{1-\alpha}\cdot \lim_{\varepsilon\to+0}(1-\varepsilon^{1-\alpha}) \end{align} $$
ここで、
$$ \lim_{\varepsilon\to+0}(1-\varepsilon^{1-\alpha})= \begin{cases} 1 & (\alpha<1のとき) \\ -\infty & (\alpha>1のとき) \end{cases} $$
よって、 \( \alpha<1 \) のときは \( \displaystyle \int_0^1\frac{1}{x^{\alpha}}dx \) は \( \frac{1}{1-\alpha} \) に収束して、 \( \alpha>1 \) のときは \( \frac{1}{1-\alpha}<0 \) より \( \displaystyle \int_0^1\frac{1}{x^{\alpha}}dx \) は \( \infty \) に発散する。
まとめると、
$$ \int_0^1\frac{1}{x^{\alpha}}dx= \begin{cases} \infty & (\alpha≧1のとき) \\ \frac{1}{1-\alpha} & (\alpha<1のとき) \end{cases} $$
(2) 実数 \( \alpha \) に対して、 \( \displaystyle \int_1^{\infty}\frac{1}{x^{\alpha}}dx \) を求める。
\( \alpha=1 \) のときは、
$$ \int_1^{\infty}\frac{1}{x}dx=\lim_{b\to\infty}\int_1^b\frac{1}{x}dx=\lim_{b\to\infty}\left[ \log x\right]_1^b=\lim_{b\to\infty}\log b=\infty $$
であるので、この広義積分は発散する。
\( \alpha\not=1 \) のときは、
$$ \begin{align} \int_1^{\infty}\frac{1}{x^{\alpha}}dx&=\lim_{b\to\infty}\int_1^b\frac{1}{x^{\alpha}}dx=\frac{1}{1-\alpha}\cdot \lim_{b\to\infty}\left[ x^{1-\alpha} \right]^b_1 \\ &=\frac{1}{1-\alpha}\cdot \lim_{b\to\infty}(b^{1-\alpha}-1) \end{align} $$
ここで、
$$ \lim_{b\to\infty}(b^{1-\alpha}-1)= \begin{cases} \infty & (\alpha<1のとき) \\ -1 & (\alpha>1のとき) \end{cases} $$
よって、 \( \alpha<1 \) のときは \( \displaystyle \int_1^{\infty}\frac{1}{x^{\alpha}}dx \) は \( \infty \) に発散して、 \( \alpha>1 \) のときは \( \displaystyle \int_1^{\infty}\frac{1}{x^{\alpha}}dx \) は \( \frac{1}{\alpha-1} \) に収束する。
まとめると、
$$ \int_1^{\infty}\frac{1}{x^{\alpha}}dx= \begin{cases} \infty & (\alpha≦1のとき) \\ \frac{1}{\alpha-1} & (\alpha>1のとき) \end{cases} $$
広義積分の収束判定
それでは、どういうときに広義積分が収束したり、発散したりするのでしょうか。
このことを調べるために、まず次の広義積分の収束・発散の関係について紹介します。
すべての \( x\in (a,b) \) に対して、 \( 0≦f(x)≦g(x) \) であるとき、次が成り立つ。
(1) 広義積分 \( \displaystyle \int_a^bg(x)dx \) が収束するならば、広義積分 \( \displaystyle \int_a^bf(x)dx \) も収束する。また、次が成り立つ。
$$ \int_a^bf(x)dx≦\int_a^bg(x)dx $$
(2) 広義積分 \( \displaystyle \int_a^bf(x)dx \) が発散するならば、広義積分 \( \displaystyle \int_a^bg(x)dx \) も発散する。
定理1の証明(気になる方だけクリックしてください)
(1) たとえば、点 \( b \) で \( f(x),g(x) \) が定義されていないとして2つの広義積分を次のように表します。
$$ \int_a^bf(x)dx=\lim_{\varepsilon\to+0}\int_a^{b-\varepsilon}f(x)dx, \quad \int_a^bg(x)dx=\lim_{\varepsilon’\to+0}\int_a^{b-\varepsilon’}g(x)dx $$
このとき、微分積分学05の記事の定理2の(2)を用いると、 \( \varepsilon≦\varepsilon’ \) のとき、
$$ \int_a^{b-\varepsilon}f(x)dx≦\int_a^{b-\varepsilon}g(x)dx $$
となります。
両辺に \( \varepsilon\to+0 \) をとると、 \( \displaystyle \lim_{\varepsilon\to+0}\int_a^{b-\varepsilon}g(x)dx \) が収束するならば、 \( 0≦f(x)≦g(x) \) より \( \displaystyle \lim_{\varepsilon\to+0}\int_a^{b-\varepsilon}f(x)dx \) も収束します。
また、 \( b-\varepsilon≦b-\varepsilon'<b \) より、 \( b-\varepsilon’\to b \) であるので、
$$ \lim_{\varepsilon\to+0}\int_a^{b-\varepsilon}f(x)dx≦\lim_{\varepsilon\to+0}\int_a^{b-\varepsilon}g(x)dx=\lim_{\varepsilon’\to+0}\int_a^{b-\varepsilon’}g(x)dx $$
したがって、
$$ \int_a^bf(x)dx≦\int_a^bg(x)dx $$
(2) これは(1)の対偶となるので、正しい。
定理1から次のことがいえます。
広義積分 \( \displaystyle \int_a^b|f(x)|dx \) が収束するならば、広義積分 \( \displaystyle \int_a^bf(x)dx \) も収束する。
定理2の証明(気になる方だけクリックしてください)
\( f(x) \) を次のように分解します。
$$ f(x)=f_+(x)-f_-(x) $$
ここで、
$$ f_+(x)=\max \{f(x),0\}, \ f_-(x)=\min \{ -f(x),0\} $$
このとき、
$$ f_+(x)+f_-(x)=|f(x)|, \quad 0≦f_+(x)≦|f(x)|, \quad 0≦f_-(x)≦|f(x)| $$
であるため、定理1より広義積分 \( \displaystyle \int_a^b|f(x)|dx \) が収束するならば、広義積分 \( \displaystyle \int_a^bf_+(x)dx \) と \( \displaystyle \int_a^bf_-(x)dx \) は収束します。
したがって、
$$ \int_a^bf(x)dx=\int_a^bf_+(x)dx-\int_a^bf_-(x)dx $$
も収束します。
広義積分の収束・発散を判定するときに、すでに収束・発散が分かっている関数との大小関係を見ることにより、定理1や定理2から求めたい広義積分の収束・発散を調べることができます。
その基準となる関数として、よく用いられるのが先ほどの例1の(1)と(2)で紹介した
$$ \int_0^1\frac{1}{x^{\alpha}}dx= \begin{cases} \infty & (\alpha≧1のとき) \\ \frac{1}{1-\alpha} & (\alpha<1のとき) \end{cases} $$
$$ \int_1^{\infty}\frac{1}{x^{\alpha}}dx= \begin{cases} \infty & (\alpha≦1のとき) \\ \frac{1}{\alpha-1} & (\alpha>1のとき) \end{cases} $$
となります。
関数 \( f(x) \) が区間 \( (a,b] \) で連続とする。
(1) $$ |f(x)|≦\frac{M}{(x-a)^{\alpha}} \quad (a<x≦b, \ \alpha<1) $$
をみたす定数 \( \alpha, \ M \) が存在するならば、広義積分
$$ \int_a^bf(x)dx=\lim_{\varepsilon\to0}\int_{a+\varepsilon}^bf(x)dx $$
は収束する。
(2) $$ f(x)≧\frac{m}{(x-a)^{\alpha}} \quad (a<x≦b, \ \alpha≧1) $$
をみたす定数 \( \alpha, \ m \) が存在するならば、広義積分
$$ \int_a^bf(x)dx=\lim_{\varepsilon\to0}\int_{a+\varepsilon}^bf(x)dx $$
は発散する。
関数 \( f(x) \) が区間 \( [a,\infty) \) で連続とする。
(1) $$ |f(x)|≦\frac{M}{x^{\alpha}} \quad (\max\{a,1\}≦x<\infty, \ \alpha>1) $$
をみたす定数 \( \alpha, \ M \) が存在するならば、広義積分
$$ \int_a^{\infty}f(x)dx=\lim_{b\to\infty}\int_a^bf(x)dx $$
は収束する。
(2) $$ f(x)≧\frac{m}{x^{\alpha}} \quad (\max\{a,1\}≦x<\infty, \ \alpha≦1) $$
をみたす定数 \( \alpha, \ m \) が存在するならば、広義積分
$$ \int_a^{\infty}f(x)dx=\lim_{b\to\infty}\int_a^bf(x)dx $$
は発散する。
定理3および定理4の証明(気になる方だけクリックしてください)
定理3の(1)のみ示します。
まず、
$$ \int_a^b\frac{M}{(x-a)^{\alpha}}dx=\lim_{\varepsilon\to+0}\int_{a+\varepsilon}^b\frac{M}{(x-a)^{\alpha}}dx $$
は、 \( y=x-a \) と変数変換することによって、
$$ \lim_{\varepsilon\to+0}\int_{a+\varepsilon}^b\frac{M}{(x-a)^{\alpha}}dx=M\lim_{\varepsilon\to+0}\int_{\varepsilon}^{b-a}\frac{1}{y^{\alpha}}dy $$
ここで、 \( \alpha>1 \) に注意して例1の(1)と同じような計算をすることにより、 \( \displaystyle \lim_{\varepsilon\to+0}\int_{\varepsilon}^{b-a}\frac{1}{y^{\alpha}}dy \) は収束します。
よって、 \( \displaystyle \int_a^b\frac{M}{(x-a)^{\alpha}}dx \) も収束し、仮定と定理1より、
$$ \int_a^b|f(x)|dx≦\int_a^b\frac{M}{(x-a)^{\alpha}}dx $$
であり、 \( \displaystyle \int_a^b|f(x)|dx \) は収束します。
したがって、定理2より、 \( \displaystyle \int_a^bf(x)dx \) も収束します。
定理3や定理4を用いた例については、下のベータ関数・ガンマ関数のところで紹介します。
ベータ関数・ガンマ関数
広義積分の重要な例として、ベータ関数とガンマ関数があります。
それらについて簡単に紹介していきたいと思います。
ベータ関数
次の関数 \( B(p,q) \) をベータ関数といいます。
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx \quad (p,q>0) $$
\( x^{p-1}(1-x)^{q-1} \) は \( 0<p<1 \) のとき \( \frac{(1-x)^{q-1}}{x^{1-p}} \ (1-p>0) \) であるので、 \( x=0 \) に近づくほど値が大きくなり、 \( x=0 \) では定義されません。
また、 \( 0<q<1 \) のとき \( \frac{x^{p-1}}{(1-x)^{1-q}} \ (1-q>0) \) であるので、 \( x=1 \) に近づくほど値が大きくなり、 \( x=1 \) では定義されません。
よって、 \( p,q \) の状況によって、ベータ関数は広義積分となります。
この積分が収束するかについて、次のことがいえます。
\( p,q>0 \) に対して、ベータ関数 \( B(p,q) \) は収束する。
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx \quad (p,q>0) $$
定理5の証明(気になる方だけクリックしてください)
まず \( p,q≧1 \) のときは、 \( B(p,q) \) は広義積分ではなく普通の積分となります。
このとき、 \( |x^{p-1}(1-x)^{q-1}| \) は閉区間 \( [0,1] \) で連続であるので、必ず最大値 \( M \) と最小値 \( m \) をもちます。
\( |x^{p-1}(1-x)^{q-1}|≧0 \) より、 \( M≧m \) かつ \( M≧|x^{p-1}(1-x)^{q-1}| \) であるので、
$$ \int_0^1|x^{p-1}(1-x)^{q-1}|dx≦\int_0^1Mdx=M\int_0^1dx=M<\infty $$
よって、 \( \displaystyle \int_0^1|x^{p-1}(1-x)^{q-1}|dx \) は有限となります。
したがって、微分積分学05の記事の定理2の(2)より、
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx $$
も有限となります。(これは広義積分の意味で収束しているということになります。)
次に、 \( 0<p<1 \) もしくは \( 0<q<1 \) とします。
このときは、
$$ \begin{align} B(p,q)&=\int_0^1x^{p-1}(1-x)^{q-1}dx \\ &=\int_0^{\frac{1}{2}}x^{p-1}(1-x)^{q-1}dx+\int_{\frac{1}{2}}^1x^{p-1}(1-x)^{q-1}dx \\ &=I_1+I_2 \end{align} $$
のように、2つの積分に分解します。
このとき、 \( 0<p<1 \) であれば \( I_1 \) が、 \( 0<q<1 \) であれば \( I_2 \) が広義積分となります。
そこで、 \( 0<p<1 \) として \( I_1 \) が収束するかを見ていきましょう。。
\( q>0 \) に対して、 \( |(1-x)^{q-1}| \) は閉区間 \( [0,\frac{1}{2}] \) で連続であるので、必ず最大値 \( M \) と最小値 \( m \) をもちます。
\( |(1-x)^{q-1}|≧0 \) より、 \( M≧m \) かつ \( M≧|(1-x)^{q-1}| \) であるので、
$$ |x^{p-1}(1-x)^{q-1}|=\frac{|(1-x)^{q-1}|}{x^{1-p}}≦\frac{M}{x^{1-p}} \quad (0<x≦\frac{1}{2}, \ 1-p<1) $$
よって、定理3の(1)と定理2より、広義積分
$$ I_1=\int_0^{\frac{1}{2}}x^{p-1}(1-x)^{q-1}dx $$
は収束します。
\( 0<q<1 \) のとき \( I_2 \) が収束することも同様に示すことができます。
したがって、
$$ B(p,q)=\int_0^1x^{p-1}(1-x)^{q-1}dx $$
は収束します。
ベータ関数の性質について、まとめておきます。
(1) $$ B(p,q)=2\int_0^{\frac{\pi}{2}}\sin^{2p-1}\theta\cos^{2q-1}\theta d\theta=B(q,p) $$
(2) \( a<b \) のとき、
$$ \int_a^b(x-a)^{p-1}(b-x)^{q-1}dx=(b-a)^{p+q-1}B(p,q) $$
(3) \( q>p>0 \) のとき、
$$ \int_0^{\infty}\frac{x^{p-1}}{(1+x)^q}dx=B(q-p,p) $$
(4) \(p>q>0 \) のとき、
$$ \int_0^{\infty}\frac{x^{q-1}}{1+x^p}dx=\frac{1}{p}B\left(\frac{q}{p},1-\frac{q}{p}\right) $$
ガンマ関数
次の関数 \( \Gamma(s) \) をガンマ関数といいます。
$$ \Gamma(s)=\int_0^{\infty}e^{-x}x^{s-1}dx \quad (s>0) $$
これは広義積分なので収束するかが大事となり、実際次のことがいえます。
\( s>0 \) に対して、ガンマ関数 \( \Gamma(s) \) は収束する。
$$ \Gamma(s)=\int_0^{\infty}e^{-x}x^{s-1}dx \quad (s>0) $$
定理7の証明(気になる方だけクリックしてください)
まず、
$$ \begin{align} \Gamma(s)&=\int_0^{\infty}e^{-x}x^{s-1}dx \\ &=\int_0^1e^{-x}x^{s-1}dx+\int_1^{\infty}e^{-x}x^{s-1}dx \\ &=I_1+I_2 \end{align} $$
のように、2つの積分に分解します。
まず、 \( I_1 \) を調べます。グラフを考えると、 \( |e^{-x}|≦1 \ (0<x≦1) \) であるので、
$$ |e^{-x}x^{s-1}|≦x^{s-1} \quad (0<x≦1) $$
よって、定理3の(1)と定理2より、広義積分
$$ I_1=\int_0^1e^{-x}x^{s-1}dx $$
は収束します。次に、 \( I_2 \) を調べます。
まず、ロピタルの定理より、
$$ \lim_{x\to\infty}e^{-x}x^{s+1}=\lim_{x\to\infty}\frac{x^{s+1}}{e^x}=\lim_{x\to\infty}\frac{\frac{d^{s+1}}{dx^{s+1}}x^{s+1}}{\frac{d^{s+1}}{dx^{s+1}}e^x}=C\lim_{x\to\infty}\frac{1}{e^x}=0 $$
ここで、 \( C \) は \( x^{s+1} \) を \( s+1 \) 回微分したときに出てくる係数である。
よって、 \( e^{-x}x^{s+1} \) は \( x \) が限りなく大きくなると値は限りなく0に小さく近づくので、(有界という言葉を知っている方は区間 \( [1,\infty) \) 上で有界なので、)
$$ |e^{-x}x^{s-1}|=\frac{e^{-x}x^{s+1}}{x^2}≦\frac{M}{x^2} \quad (1≦x<\infty) $$
となる \( M \) が存在する。したがって、定理4の(1)と定理2より、広義積分
$$ I_2=\int_1^{\infty}e^{-x}x^{s-1}dx $$
は収束します。よって、 \( I_1 \) と \( I_2 \) を合わせると広義積分
$$ \Gamma(s)=\int_0^{\infty}e^{-x}x^{s-1}dx \quad (s>0) $$
は収束します。
ガンマ関数の性質について、まとめておきます。
(1) $$ \Gamma(s+1)=s\Gamma(s) $$
(2) $$ \Gamma(1)=1 $$
(3) $$ \Gamma(n+1)=n! \quad (n:自然数) $$
(4) $$ \Gamma(s)>0 $$
(5)
$$ 2\int_0^{\infty}e^{-x^2}x^{2s-1}dx=\Gamma(s) $$
また、ベータ関数とガンマ関数との関係は次のようになります。
$$ B(p,q)=\frac{\Gamma(p)\Gamma(q)}{\Gamma(p+q)} \quad (p,q>0) $$
ガンマ関数の性質を続けます。
(1) $$ \int_0^{\frac{\pi}{2}}\sin^{2s-1}\theta\cos^{2r-1}\theta d\theta=\frac{1}{2}\frac{\Gamma(s)\Gamma(r)}{\Gamma(s+r)} \quad (s,r>0) $$
(2) $$ \int_0^{\frac{\pi}{2}}\sin^n\theta d\theta=\frac{\Gamma\left(\frac{n+1}{2}\right) \Gamma\left(\frac{1}{2} \right)}{2\Gamma\left( \frac{n}{2}+1 \right)}, \quad (n>-1) $$
(3) $$ \Gamma\left(\frac{1}{2} \right)=\sqrt{\pi} $$
(4) $$ \int_0^{\infty}e^{-x^2}dx=\frac{1}{2}\Gamma \left( \frac{1}{2} \right) =\frac{\sqrt{\pi}}{2} $$
(5) $$ \int_0^1\left(\log \frac{1}{x} \right)^{s-1}dx=\Gamma (s) $$
(6) \( p>q>0 \) のとき、
$$ \int_0^{\infty}\frac{x^{q-1}}{1+x^p}=\frac{1}{p}\Gamma\left(\frac{q}{p} \right)\Gamma\left( 1-\frac{q}{p} \right) $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

