こんにちは、ひかりです。
今回は微分積分学から双曲線関数と逆双曲線関数について解説していきます。
この記事では以下のことを紹介します。
- 双曲線関数について
- 双曲線関数の性質と三角関数との比較について
- 逆双曲線関数について
双曲線関数
双曲線正弦関数・双曲線余弦関数・双曲線正接関数
双曲線関数というものを次のように定義します。
双曲線正弦関数 \( y=\sinh x \) (ハイパボリックサイン)、双曲線余弦関数 \( y=\cosh x \) (ハイパボリックコサイン)、双曲線正接関数 \( y=\tanh x \) (ハイパボリックタンジェント)を次のように定める。
$$ \begin{align} \sinh x&=\frac{e^x-e^{-x}}{2} \\ \cosh x&=\frac{e^x+e^{-x}}{2} \\ \tanh x&=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}} \end{align} $$
ここで、 \( e^x \) とはネイピア数 \( e \) の指数関数となります。
なぜ、この関数が双曲線関数と言われているのでしょうか。
それは媒介変数 \( t \) を用いて、 \( (x,y)=(\cosh t,\sinh t) \) と媒介変数表示をすると、 \( x^2-y^2=1 \) (つまり、双曲線の式)をみたすからです。
確かめてみると、
$$ \begin{align} x^2-y^2&=(\cosh t)^2-(\sinh t)^2 \\ &=\left( \frac{e^t+e^{-t}}{2} \right)^2-\left( \frac{e^t-e^{-t}}{2} \right)^2 \\ &=\frac{(e^{2t}+2+e^{-2t})-(e^{2t}-2+e^{-2t})}{4}=1 \end{align} $$
また、グラフは次のようになります。
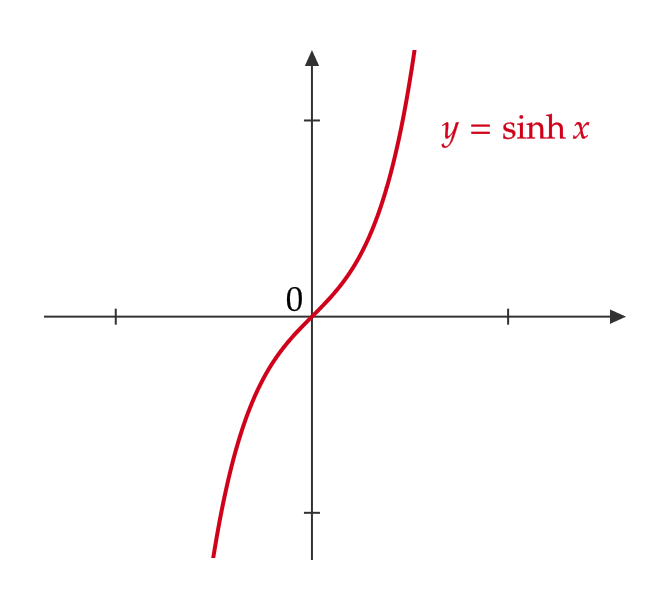
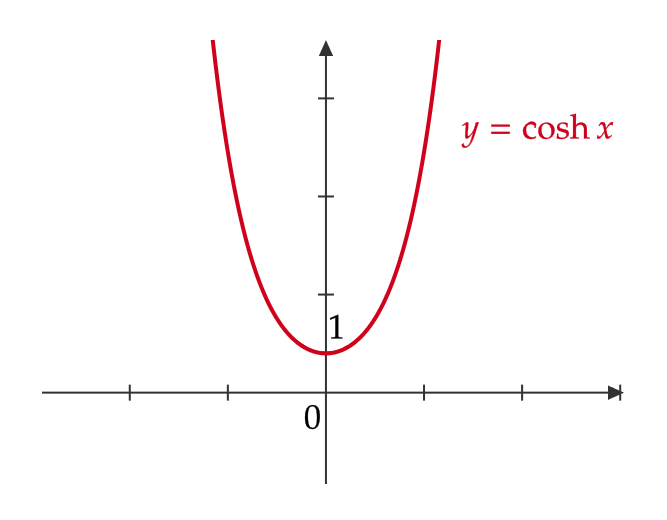
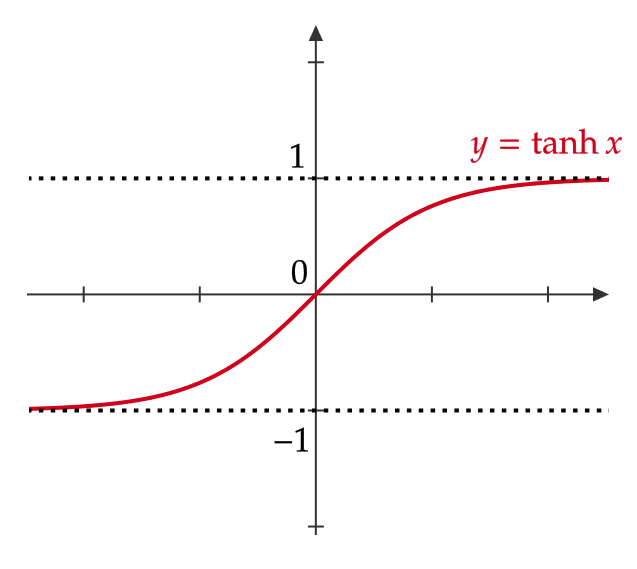
双曲線余割関数・双曲線正割関数・双曲線余接関数
三角関数の場合と同様に、 \( \sinh x, \ \cosh x, \ \tanh x \) の逆数をそれぞれ \( \text{csch} \ x \) (ハイパボリックコセカント)、 \( \text{sech} \ x, \) (ハイパボリックセカント)、 \( \text{coth} \ x \) (ハイパボリックコタンジェント)と表します。つまり、
$$ \begin{align} \text{csch} \ x&=\frac{1}{\sinh x}=\frac{2}{e^x-e^{-x}} \quad (x\not=0) \\ \text{sech} \ x&=\frac{1}{\cosh x}=\frac{2}{e^x+e^{-x}} \\ \text{coth} \ x&=\frac{1}{\tanh x}=\frac{e^x+e^{-x}}{e^x-e^{-x}} \quad (x\not=0) \end{align} $$
これらはそれぞれ双曲線余割関数、双曲線正割関数、双曲線余接関数と呼びます。
グラフは次のようになります。
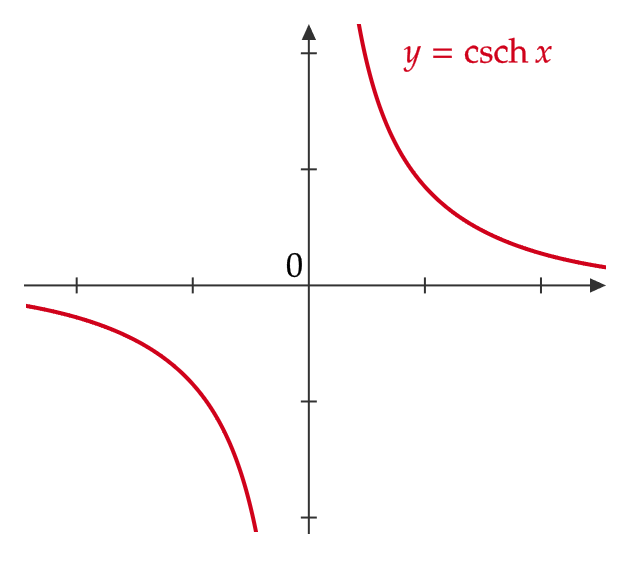
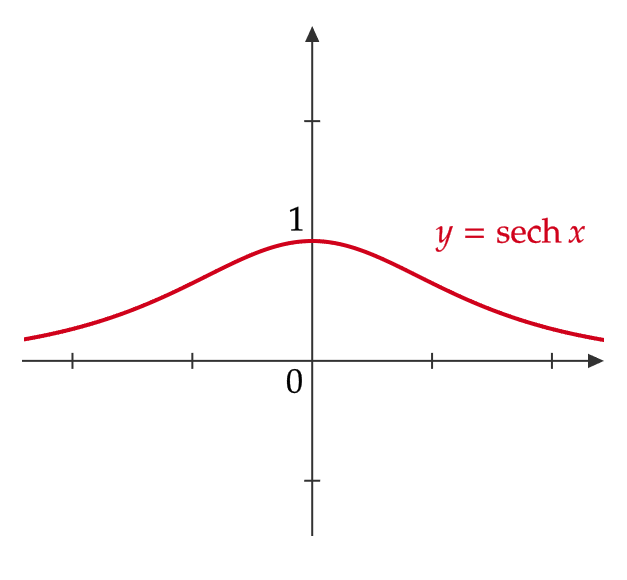
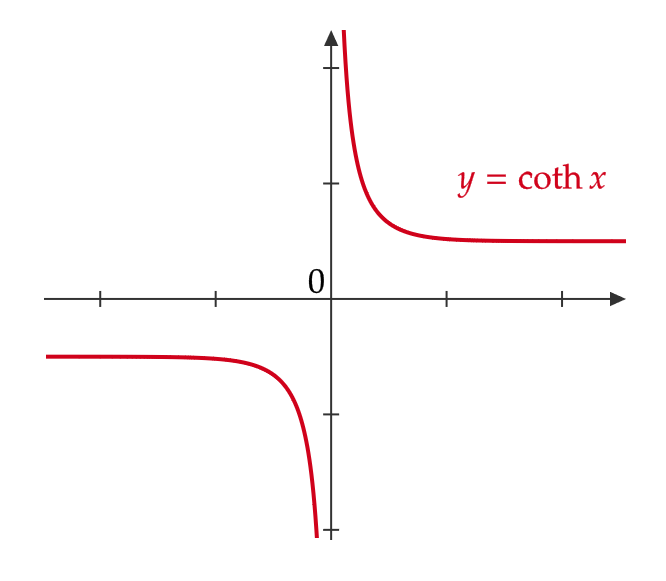
双曲線関数の性質
双曲線関数は三角関数の性質と似たような性質が成り立ちます。
それぞれを比較しながら見ていきましょう。
三角関数の性質
$$ \frac{\sin x}{\cos x}=\tan x $$
$$ \cos^2 x+\sin^2 x=1 $$
$$ 1+\tan^2x=\frac{1}{\cos^2x} $$
$$ \sin(x\pm y)=\sin x\cos y\pm\cos x\sin y $$
$$ \cos(x\pm y)=\cos x\cos y\mp\sin x\sin y $$
$$ \tan(x\pm y)=\frac{\tan x\pm \tan y}{1\mp \tan x\tan y} $$
$$ \cot x=\frac{\cos x}{\sin x} $$
$$ 1+\tan^2x=\sec^2x $$
$$ \cot^2x+1=\csc^2x $$
双曲線関数の性質
$$ \frac{\sinh x}{\cosh x}=\tanh x $$
$$ \cosh^2 x\color{red}{-}\sinh^2 x=1 $$
$$ 1\color{red}{-}\tanh^2x=\frac{1}{\cosh^2 x} $$
$$ \sinh(x\pm y)=\sinh x\cosh y\pm\cosh x\sinh y $$
$$ \cosh(x\pm y)=\cosh x\cosh y\color{red}{\pm}\sinh x\sinh y $$
$$ \tanh(x\pm y)=\frac{\tanh x\pm \tanh y}{1\color{red}{\pm} \tanh x\tanh y} $$
$$ \coth x=\frac{\cosh x}{\sinh x} $$
$$ 1\color{red}{-}\tanh^2x=\text{sech}^2 \ x $$
$$ \coth^2x\color{red}{-}1=\text{csch}^2 \ x $$
双曲線関数の性質の証明(気になる方だけクリックしてください)
次の3つのみ示す。
$$ 1-\tanh^2x=\frac{1}{\cosh^2 x} $$
$$ \cosh(x+ y)=\cosh x\cosh y+\sinh x\sinh y $$
$$ \coth^2x-1=\text{csch}^2 \ x $$
まず、1つ目は
$$ \begin{align} 1-\tanh^2x&=1-\left( \frac{e^x-e^{-x}}{e^x+e^{-x}}\right)^2=1-\frac{e^{2x}-2+e^{-2x}}{e^{2x}+2+e^{-2x}} \\ &=\frac{(e^{2x}+2+e^{-2x})-(e^{2x}-2+e^{-2x})}{e^{2x}+2+e^{-2x}} \\ &=\frac{4}{e^{2x}+2+e^{-2x}}=\left( \frac{2}{e^x+e^{-x}} \right)^2=\frac{1}{\cosh^2x} \end{align} $$
2つ目は
$$ \begin{align} &\cosh x\cosh y+\sinh x\sinh y \\ &=\frac{e^x+e^{-x}}{2}\cdot \frac{e^y+e^{-y}}{2}+\frac{e^x-e^{-x}}{2}\cdot\frac{e^y-e^{-y}}{2} \\ &=\frac{1}{4}\{ e^{x+y}+e^{x-y}+e^{-(x-y)}+e^{-(x+y)}\} \\ & \quad +\frac{1}{4}\{ e^{x+y}-e^{x-y}-e^{-(x-y)}+e^{-(x+y)} \} \\ &=\frac{1}{4}\{ 2e^{x+y}+2e^{-(x+y)}\}=\cosh (x+y) \end{align} $$
3つ目は
$$ \begin{align} \coth^2x-1&=\left( \frac{e^x+e^{-x}}{e^x-e^{-x}} \right)^2-1=\frac{e^{2x}+2+e^{-2x}}{e^{2x}-2+e^{-2x}}-1 \\ &=\frac{(e^{2x}+2+e^{-2x})-(e^{2x}-2+e^{-2x})}{e^{2x}-2+e^{-2x}} \\ &=\frac{4}{e^{2x}-2+e^{-2x}}=\left( \frac{2}{e^x-e^{-x}} \right)^2=\text{csch}^2 \ x \end{align} $$
逆双曲線関数
逆双曲線正弦関数・逆双曲線余弦関数・逆双曲線正接関数
双曲線関数の逆関数についても三角関数と同様に、定義域を制限することにより存在します。
\( \sinh x, \ \cosh x, \ \tanh x \) の逆関数をそれぞれ \( \sinh^{-1}x, \ \cosh^{-1}x, \ \tanh^{-1}x \) もしくは \( \text{arcsinh} \ x \) (アークハイパボリックサイン), \( \text{arccosh} \ x \) (アークハイパボリックコサイン), \( \text{arctanh} \ x \) (アークハイパボリックタンジェント)と表します。
これらはそれぞれ逆双曲線正弦関数、逆双曲線余弦関数、逆双曲線正接関数と呼びます。
逆関数を考える際のそれぞれの関数の定義域と値域を表にまとめておきます。
| 関数 | 定義域 | 値域 |
| \( y=\sinh x \) | 実数全体 | 実数全体 |
| \( y=\cosh x \) | \( x≧0 \) | \( y≧ 1 \) |
| \( y=\tanh x \) | 実数全体 | \( -1<y<1 \) |
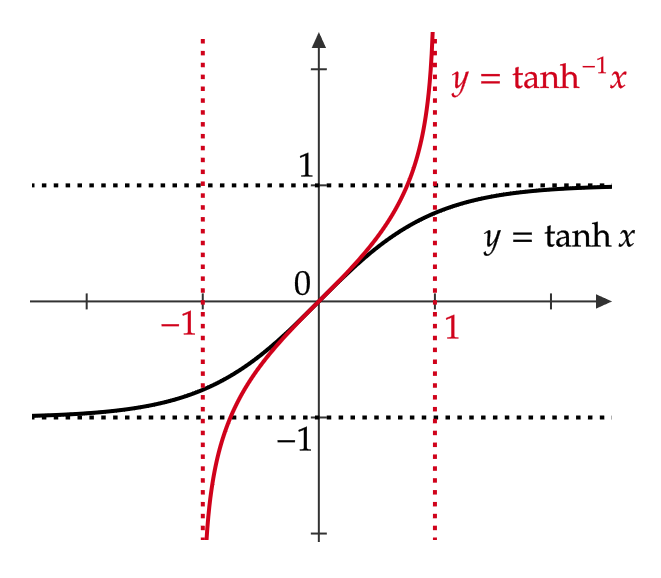
| \( y=\sinh^{-1}x \) | 実数全体 | 実数全体 |
| \( y=\cosh^{-1}x \) | \( x≧ 1 \) | \( y≧0 \) |
| \( y=\tanh^{-1}x \) | \( -1<x<1 \) | 実数全体 |
また、グラフは次のようになります。
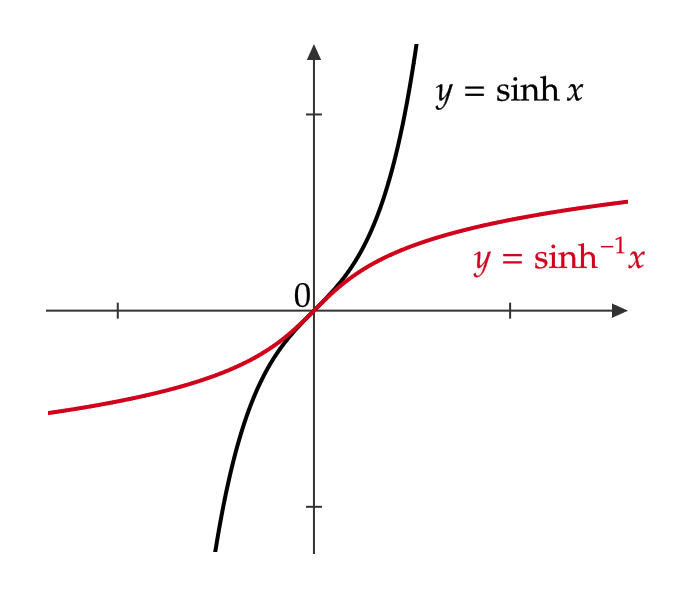
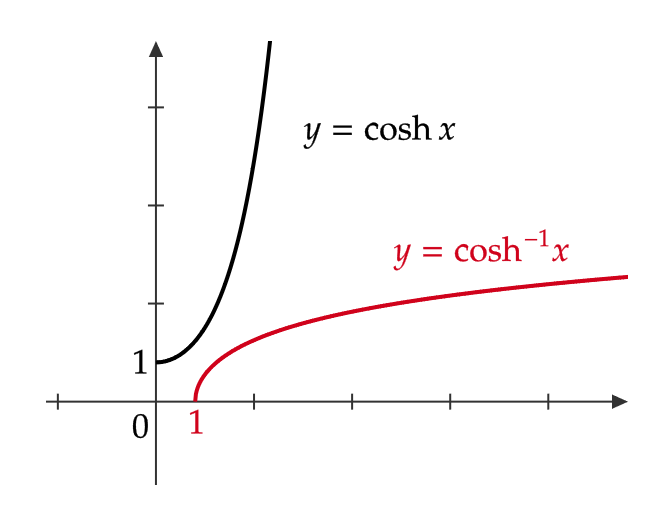
逆双曲線余割関数・逆双曲線正割関数・逆双曲線余接関数
\( \text{csch} \ x, \ \text{sech} \ x, \ \text{coth} \ x \) の逆関数をそれぞれ \( \text{csch}^{-1} \ x, \ \text{sech}^{-1} \ x, \ \text{coth}^{-1} \ x \) もしくは \( \text{arccsch} \ x \) (アークハイパボリックコセカント), \( \text{arcsech} \ x \) (アークハイパボリックセカント), \( \text{arccoth} \ x \) (アークハイパボリックコタンジェント)と表します。
これらはそれぞれ逆双曲線余割関数、逆双曲線正割関数、逆双曲線余接関数と呼びます。
逆関数を考える際のそれぞれの関数の定義域と値域を表にまとめておきます。
| 関数 | 定義域 | 値域 |
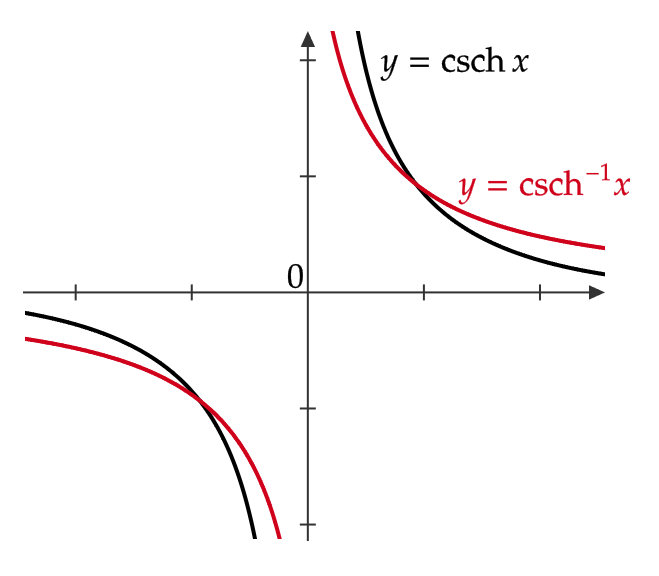
| \( y=\text{csch} x \) | \( x<0, \ x>0 \) | \( y<0, \ y>0 \) |
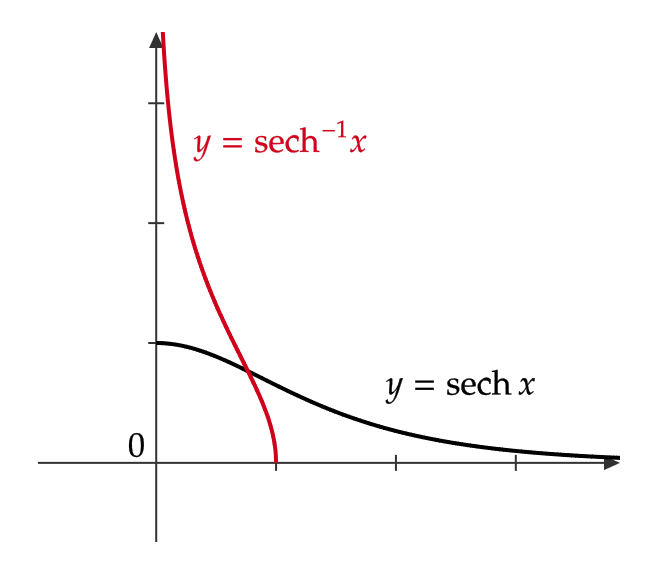
| \( y=\text{sech} x \) | \( x≧0 \) | \( 0<y≦ 1 \) |
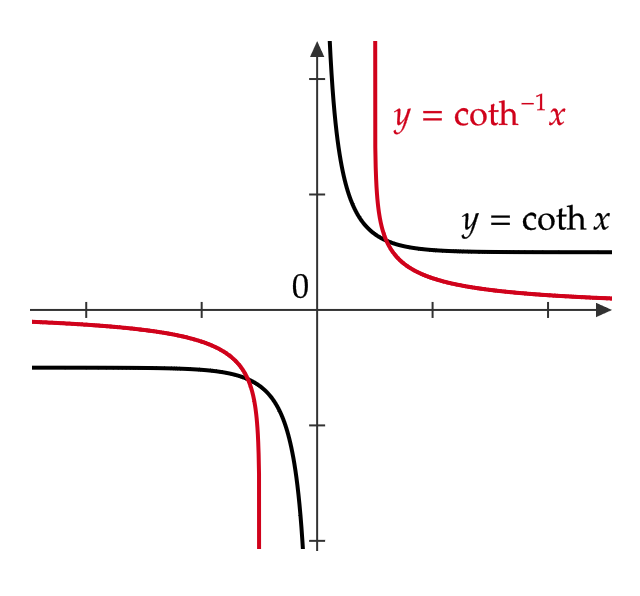
| \( y=\text{coth} x \) | \( x<0, \ x>0 \) | \( y<-1, \ y>1 \) |
| \( y=\text{csch}^{-1} \ x \) | \( x<0, \ x>0 \) | \( y<0, \ y>0 \) |
| \( y=\text{sech}^{-1} \ x \) | \( 0<x≦ 1 \) | \( y≧0 \) |
| \( y=\text{coth}^{-1} \ x \) | \( x<-1, \ x>1 \) | \( y<0, \ y>0 \) |
また、グラフは次のようになります。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

