こんにちは、ひかりです。
今回は線形代数学からベクトルについて解説していきます。
この記事では以下のことを紹介します。
- ベクトルとは何か?
- 2つのベクトルが等しいとは何か?
- ベクトルの演算(和とスカラー倍)について
- ベクトルの演算に関する性質について
ベクトルの定義
高校までの数学では、自然数や実数などさまざまな数を勉強してきました。
それらの数を一つ一つ考えるのではなく、いくつかの数をひとまとめにして考えたものをベクトルといいます。
ベクトルは直線の矢印で表現することができます。
$$ (2,1) \ または \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$
を座標に図示すると、図のような直線となる。
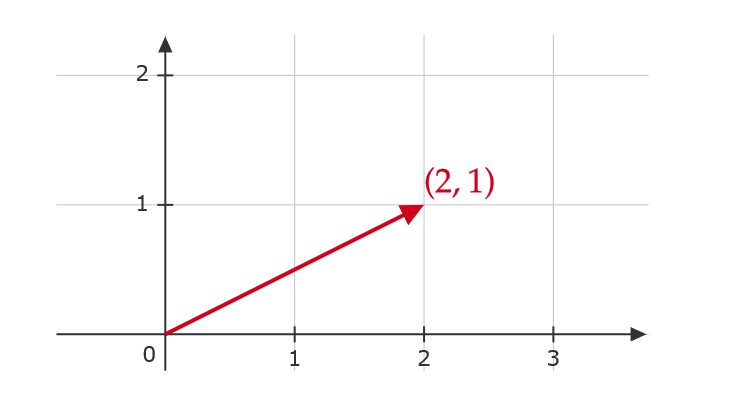
例1では、2個の数をひとまとめにしたものとなりますが、2個に限らず \( n \) 個の数を考えることができます。
そのため、きちんとベクトルを定義しておきましょう。
\( n\) 個の数 \( a_1,a_2,\dots,a_n \) を並べた組 \( (a_1,a_2,\dots,a_n) \) を \( n\) 次元ベクトルといい、各々の数 \( a_1,a_2,\dots,a_n\) をその成分という。
成分を縦に並べた組 \( \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} \) を列ベクトルといい、横に並べた組 \( (a_1,a_2,\dots,a_n) \) を行ベクトルという。
列ベクトルと行ベクトルがありますが、現時点では同じものと思っていただいて問題ないです。
また、ベクトルは \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} \) のように1文字で表すときがあります。
(1) $$ \mathbf{a}=\begin{pmatrix} 2 \\ 1 \end{pmatrix} \ もしくは \ \mathbf{a}=(2,1) $$
は、2次元ベクトルとなる。
(2次元ベクトルのことを平面ベクトルともいう)
(2) $$ \mathbf{b}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \ もしくは \ \mathbf{b}=(1,2,3) $$
は、3次元ベクトルとなる。
(3次元ベクトルのことを空間ベクトルともいう)
ベクトルの相等
2つのベクトルが等しいとはどういうことかを定義しておきましょう。
2つのベクトルの各成分が等しいとき、この2つのベクトルは等しいという。
つまり、数式を用いて表現すると、2つのベクトル
$$ \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}, \quad \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} $$
に対して、 \( \mathbf{a}=\mathbf{b} \) であるとは、
$$ a_1=b_1, \quad a_2=b_2, \quad \dots, \quad a_n=b_n $$
となることをいう。
(1) \( \mathbf{a}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \) のとき、 \( \mathbf{a}=\mathbf{b} \) である。
(2) \( \mathbf{a}=\begin{pmatrix} 2 \\ 2 \\ 2 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} \) のとき、 \( \mathbf{a} \) と \( \mathbf{b} \) は等しくない。
(1つでも成分が異なる場合は2つのベクトルは等しくない)
(3) \( \mathbf{a}=\begin{pmatrix} 0 \\ 0 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \) のとき、 \( \mathbf{a} \) と \( \mathbf{b} \) は等しくない。
(一見、同じように見えるが、異なる次元のベクトルは等しくない)
ベクトルの演算(和とスカラー倍)
実数や複素数において、足し算や掛け算が存在していました。
同様に、ベクトルに対しても次のようにして和とスカラー倍を定義します。
2つの \( n \) 次元ベクトル \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} \) と \( \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} \) と実数 \( k \) に対して、和とスカラー倍を次のように定めます。
ベクトルの和: \( \mathbf{a}+\mathbf{b}=\begin{pmatrix} a_1+b_1 \\a_2+b_2 \\ \vdots \\a_n+b_n \end{pmatrix} \)
ベクトルのスカラー倍: \( k\mathbf{a}=\begin{pmatrix} ka_1 \\ ka_2 \\ \vdots \\ ka_n \end{pmatrix} \)
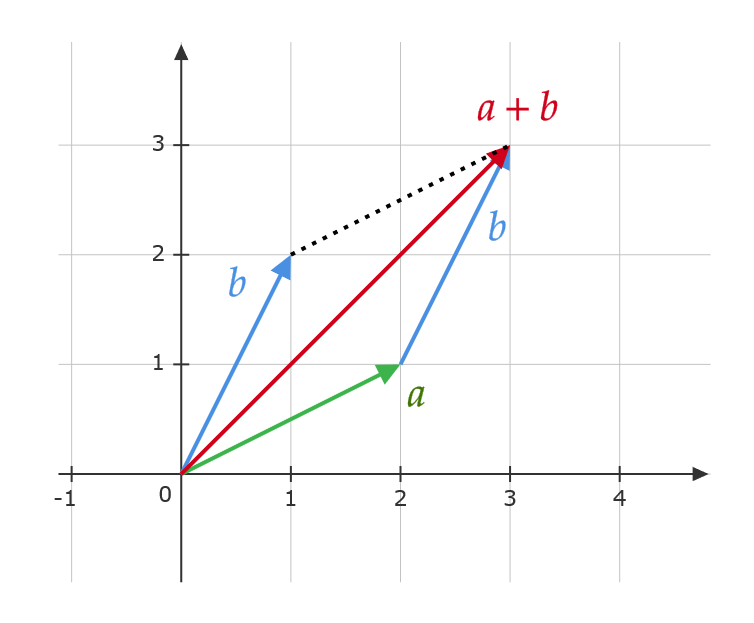
\( \mathbf{a}=\begin{pmatrix} 2 \\ 1 \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} 1 \\ 2 \end{pmatrix} \) とする。
和: \( \mathbf{a}+\mathbf{b}=\begin{pmatrix} 2+1 \\ 1+2 \end{pmatrix}=\begin{pmatrix} 3 \\ 3 \end{pmatrix} \)
図で考えると、 \( \mathbf{a} \) と \( \mathbf{b} \) を2辺とする平行四辺形の対角線を表すベクトルが \( \mathbf{a}+\mathbf{b} \) となる。
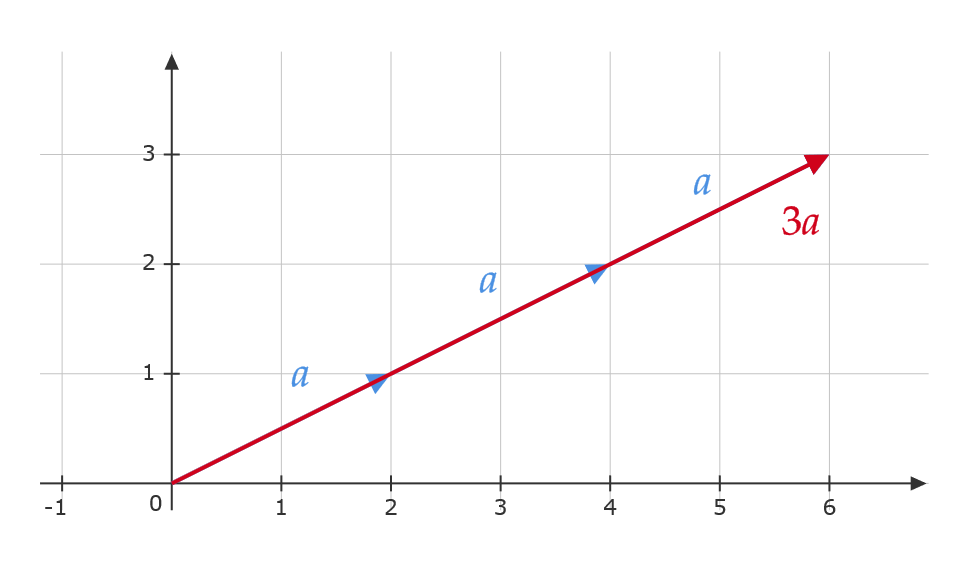
スカラー倍: \( 3\mathbf{a}=\begin{pmatrix} 3\times 2 \\ 3\times 1 \end{pmatrix}=\begin{pmatrix} 6 \\ 3 \end{pmatrix} \)
図で考えると、 \( \mathbf{a} \) と同じ向きで3倍の長さを表すベクトルが \( 3\mathbf{a} \) となる。
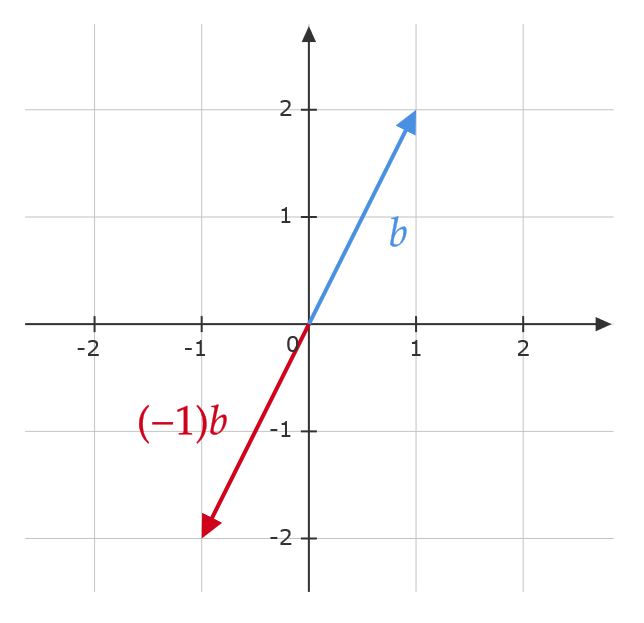
スカラー倍: \( (-1)\mathbf{b}=\begin{pmatrix} -1\times 1 \\ -1\times 2 \end{pmatrix}=\begin{pmatrix} -1 \\ -2 \end{pmatrix} \)
図で考えると、 \( \mathbf{b} \) と反対の向きで1倍の長さを表すベクトルが \( (-1)\mathbf{b} \) となる。
ここで、2つの特別なベクトルについて紹介します。
(1) ベクトル \( \mathbf{a} \) に対して、 \( (-1)\mathbf{a} \) を \( \mathbf{a} \) の逆ベクトルといい、 \( -\mathbf{a} \) で表す。つまり、
$$ \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} \ に対して、 \ -\mathbf{a}=\begin{pmatrix} -a_1 \\ -a_2 \\ \vdots \\ -a_n \end{pmatrix} $$
(2) すべての成分が0であるベクトルをゼロベクトルといい、 \( \mathbf{0} \) で表す。つまり、
$$ \mathbf{0}=\begin{pmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{pmatrix} $$
また、ベクトルの和の定義から、ベクトルの差を定義することができます。
2つのベクトル \( \mathbf{a},\mathbf{b} \) に対して、差 \( \mathbf{a}-\mathbf{b} \) を \( \mathbf{a}+(-\mathbf{b}) \) で定める。
ベクトルの演算(和とスカラー倍)に関する性質
ベクトルの和とスカラー倍に関する性質についていくつか紹介します。
基本的には通常の数の性質と似たような性質になります。
ベクトル \( \mathbf{a},\mathbf{b},\mathbf{c} \) と実数 \( k,h \) に対して、次が成り立つ。
(1) \( \mathbf{a}+\mathbf{b}=\mathbf{b}+\mathbf{a} \) (交換法則)
(2) \( (\mathbf{a}+\mathbf{b})+\mathbf{c}=\mathbf{a}+(\mathbf{b}+\mathbf{c}) \) (結合法則)
(3) \( \mathbf{a}+\mathbf{0}=\mathbf{a}, \ \mathbf{a}+(-\mathbf{a})=\mathbf{0} \)
(4) \( k(\mathbf{a}+\mathbf{b})=k\mathbf{a}+k\mathbf{b} \) (分配法則)
(5) \( (k+h)\mathbf{a}=k\mathbf{a}+h\mathbf{a} \) (分配法則)
(6) \( (kh)\mathbf{a}=k(h\mathbf{a}) \) (結合法則)
(7) \( 1\mathbf{a}=\mathbf{a} \)
定理1の証明(気になる方だけクリックしてください)
(1)と(4)を示していきます。
(1) \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} \) とおきます。このとき、
$$ \begin{align} \mathbf{a}+\mathbf{b}&=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}+\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}=\begin{pmatrix} a_1+b_1 \\ a_2+b_2 \\ \vdots \\ a_n+b_n \end{pmatrix} \\ &=\begin{pmatrix} b_1+a_1 \\ b_2+a_2 \\ \vdots \\ b_n+a_n \end{pmatrix}=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}+\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}=\mathbf{b}+\mathbf{a} \end{align} $$
(4) \( \mathbf{a}=\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}, \ \mathbf{b}=\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} \) とおきます。このとき、
$$ \begin{align} k(\mathbf{a}+\mathbf{b})&=k\left(\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}+\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix}\right)=k\begin{pmatrix} a_1+b_1 \\ a_2+b_2 \\ \vdots \\ a_n+b_n \end{pmatrix} \\ &=\begin{pmatrix} k(a_1+b_1) \\ k(a_2+b_2) \\ \vdots \\ k(a_n+b_n) \end{pmatrix}=\begin{pmatrix} ka_1+kb_1 \\ ka_2+kb_2 \\ \vdots \\ ka_n+kb_n \end{pmatrix} \\ &=\begin{pmatrix} ka_1 \\ ka_2 \\ \vdots \\ ka_n \end{pmatrix}+\begin{pmatrix} kb_1 \\ kb_2 \\ \vdots \\ kb_n \end{pmatrix}=k\begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix}+k\begin{pmatrix} b_1 \\ b_2 \\ \vdots \\ b_n \end{pmatrix} \\ &=k\mathbf{a}+k\mathbf{b} \end{align} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

