こんにちは、ひかりです。
今回は高校数学から媒介変数表示と極座標変換について解説していきます。
この記事では以下のことを紹介します。
- 媒介変数表示について
- 極座標と極方程式について
- 2次曲線の極方程式について
媒介変数表示
媒介変数表示
半径 \( r \) の円周上を動く点 \( P=(x,y) \) について考えましょう。
高校数学(数学Ⅲ)03の記事より、動径 \( OP \) の表す角を \( t \) とすると、
$$ \begin{cases} x=r\cos t \\ y=r\sin t \end{cases} $$
と表されることを学びました。
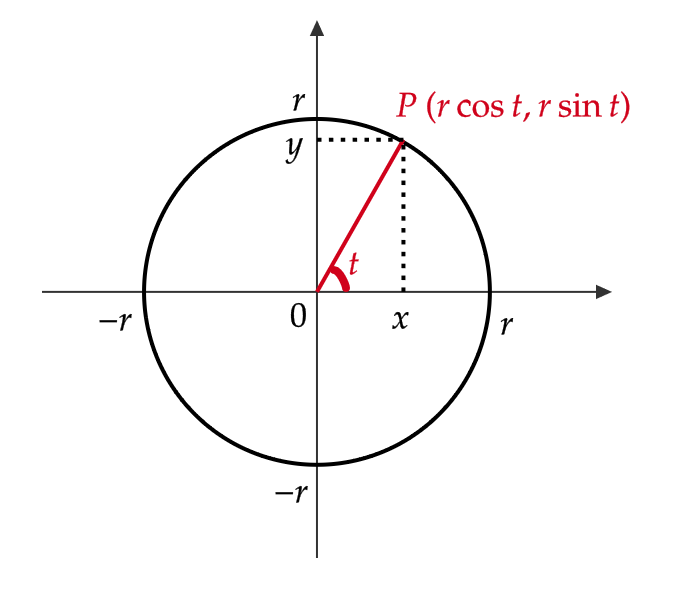
このとき、 \( t \) が実数全体を動くとき、点 \( P=(x,y) \) はこの円周上を動くことになります。
つまり、2つの変数 \( x,y \) は1つの変数 \( t \) によってつながっている( \( t \) が \( x,y \) を媒介している)ということになります。
このように、平面上の曲線がある変数 \( t \) によって、
$$ \begin{cases} x=f(t) \\ y=g(t) \end{cases} $$
で表されるとき、これをその曲線の媒介変数表示といい、 \( t \) を媒介変数といいます。
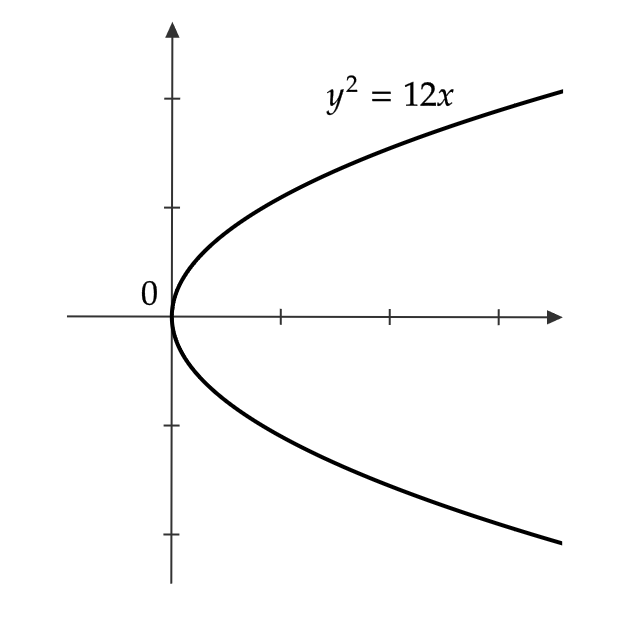
(1) \( \begin{cases} x=3t^2 \\ y=6t \end{cases} \) をみたす点 \( P=(x,y) \) は、どのような曲線上を動くかを調べる。
第2式より、 \( t=\frac{y}{6} \) であるので、第1式に代入すると、 \( x=3\left( \frac{y}{6} \right)^2 \)
よって、 \( x=\frac{y^2}{12} \) なので、 \( y^2=12x \)
したがって、点 \( P \) は放物線 \( y^2=12x \) 上を動く。
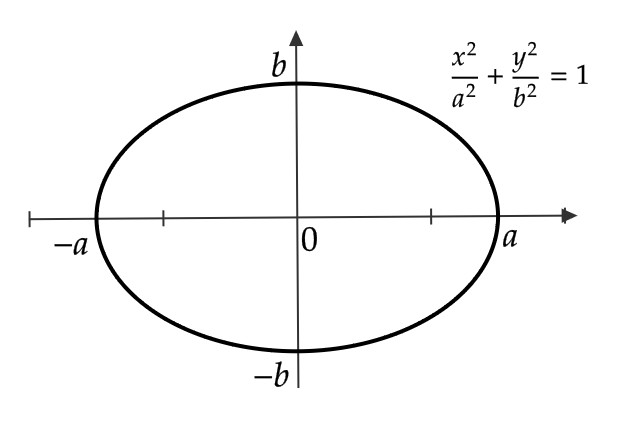
(2) \( \begin{cases} x=a\cos t \\ y=b\sin t \end{cases} \) をみたす点 \( P=(x,y) \) は、どのような曲線上を動くかを調べる。
それぞれ、 \( \frac{x}{a}=\cos t, \ \frac{y}{b}=\sin t \) となる。
ここで、 \( \cos^2 t+\sin^2t=1 \) であるので、
$$ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $$
したがって、点 \( P \) は楕円 \( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \) 上を動く。
媒介変数表示された曲線の平行移動
曲線 \( \begin{cases} x=f(t) \\ y=g(t) \end{cases} \) 上の点 \( (x,y) \) を \( x \) 軸方向に \( m \) 、 \( y \) 軸方向に \( n \) だけ平行移動した点を \( (X,Y) \) とすると、
$$ X=x+m=f(t)+m $$
$$ Y=y+m=g(t)+n $$
となります。
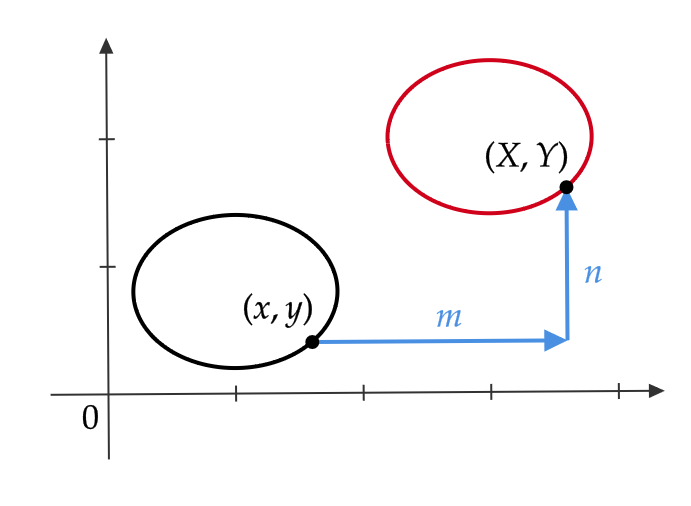
したがって、次のことがいえます。
曲線 \( \begin{cases} x=f(t) \\ y=g(t) \end{cases} \) を \( x \) 軸方向に \( m \) 、 \( y \) 軸方向に \( n \) だけ平行移動した曲線は
$$ \begin{cases} x=f(t)+m \\ y=g(t)+n \end{cases} $$
である。
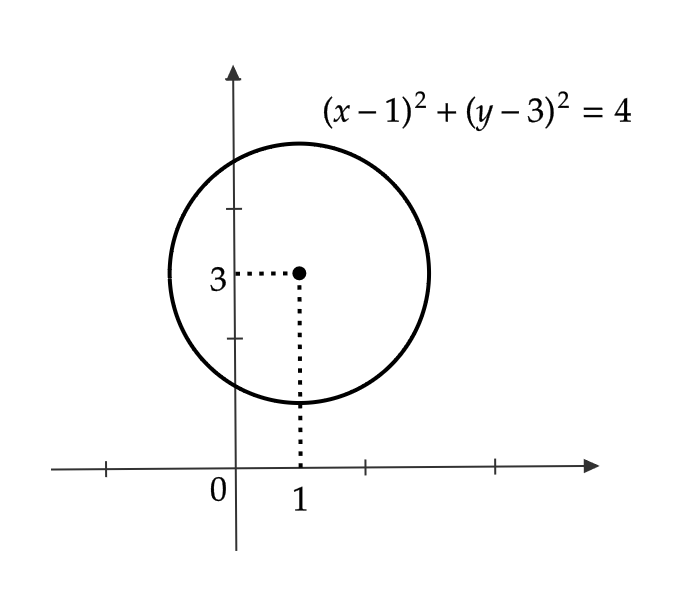
媒介変数表示 \( \begin{cases} x=2\cos t+1 \\ y=2\sin t+3 \end{cases} \) はどのような曲線を表すかを調べる。
これは
$$ \begin{cases} x=2\cos t \\ y=2\sin t \end{cases} \tag{1} $$
を \( x \) 軸方向に \( 1 \) 、 \( y \) 軸方向に \( 3 \) だけ平行移動した曲線となっている。
式(1)は例1(2)より、 \( \frac{x^2}{4}+\frac{y^2}{4}=1 \) という曲線を表す。
これは、つまり半径2の円 \( x^2+y^2=4 \) である。
よって、求めたい式の曲線は半径2の円を \( x \) 軸方向に \( 1 \) 、 \( y \) 軸方向に \( 3 \) だけ平行移動した円
$$ (x-1)^2+(y-3)^2=4 $$
となっている。
極座標と極方程式
極座標
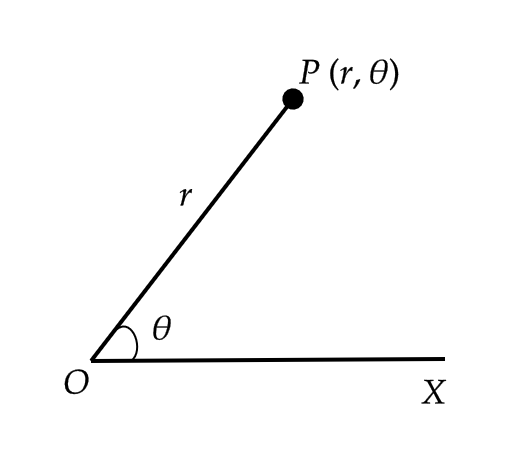
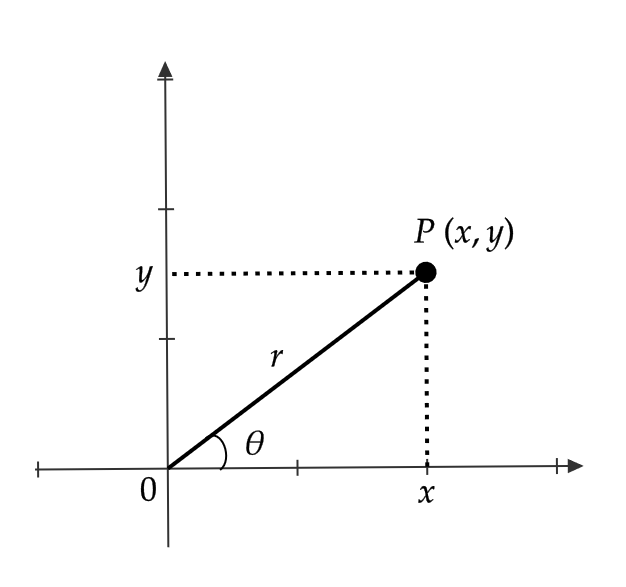
平面上に点 \( O \) と半直線 \( OX \) を定めると、平面上の点 \( P \) を、 \( O \) からの距離 \( r \) と、 \( OX \) と \( OP \) のなす角 \( \theta \) で定めることができます。
このとき、 \( (r,\theta) \) を点 \( P \) の極座標といい、点 \( O \) を極、 \( \theta \) を偏角、 \( r \) を動径 \( OP \) の長さといいます。
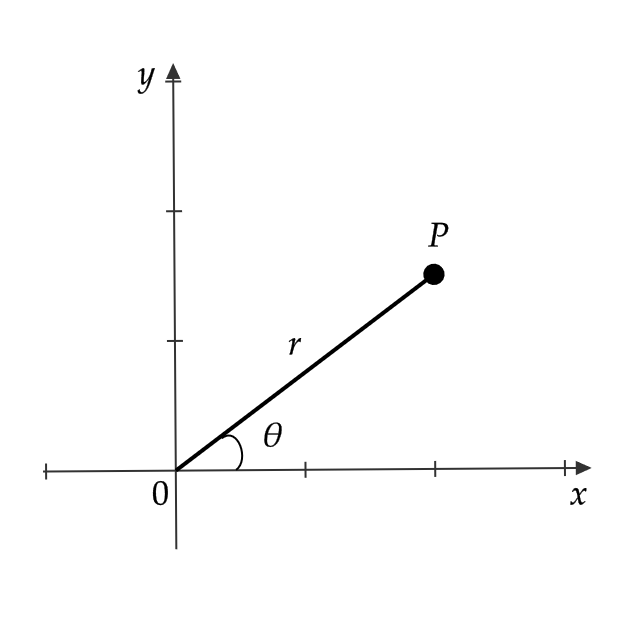
極座標に対して、いままで用いてきた \( x,y \) 座標のことを直交座標といいます。
直交座標 \( (x,y) \) を極座標 \( (r,\theta) \) を用いて表すと、
$$ x=r\cos \theta, \quad y=r\sin \theta $$
という関係が成り立ちます。
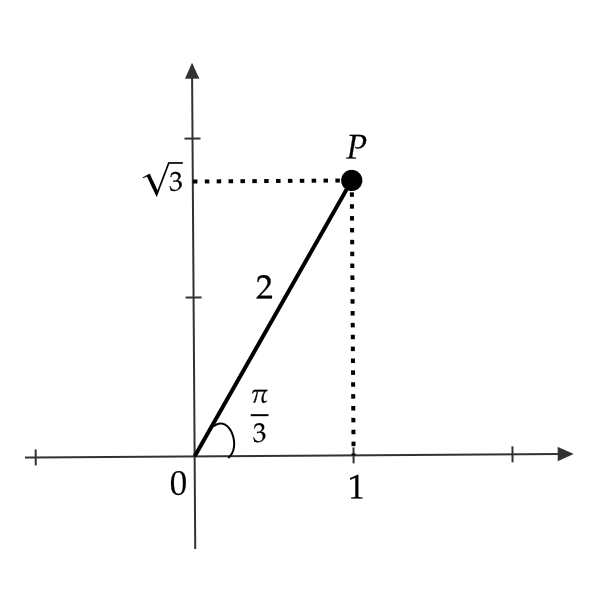
極座標が \( (2,\frac{\pi}{3}) \) である点 \( P \) の直交座標 \( (x,y) \) を求める。
$$ x=r\cos \theta=2\cos \frac{\pi}{3}=1 $$
$$ y=r\sin\theta=2\sin \frac{\pi}{3}=\sqrt{3} $$
であるので、 \( P \) の直交座標は \( (1,\sqrt{3}) \)
点 \( P \) の直交座標 \( (x,y) \) と極座標 \( (r,\theta) \) の間の関係として、次が成り立つ。
$$ \sin \theta=\frac{y}{r}, \ \cos \theta=\frac{x}{r}, \ \tan\theta=\frac{y}{x} $$
$$ r=\sqrt{x^2+y^2} $$
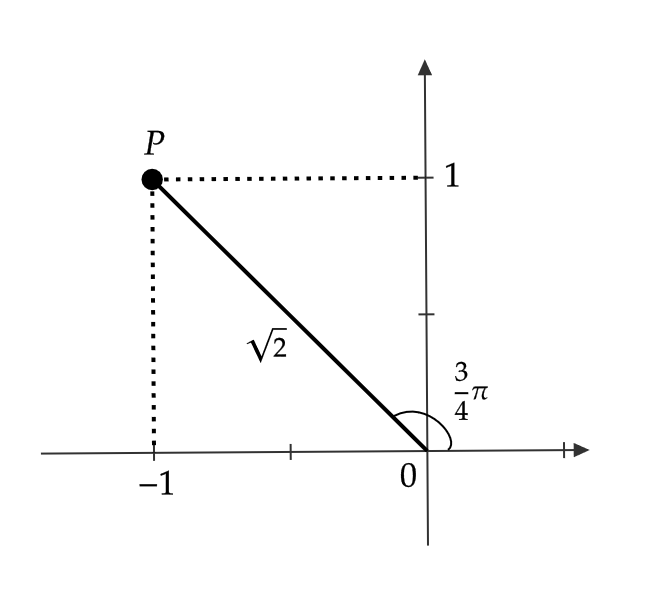
直交座標が \( (-1,1) \) である点 \( P \) の極座標 \( (r,\theta) \) を求める。
$$ r=\sqrt{x^2+y^2}=\sqrt{(-1)^2+1^2}=\sqrt{2} $$
であるので
$$ \cos\theta=\frac{x}{r}=\frac{-1}{\sqrt{2}}, \ \sin\theta=\frac{y}{r}=\frac{1}{\sqrt{2}} $$
\( 0≦ \theta<2\pi \) で考えると、 \( \theta=\frac{3}{4}\pi \)
よって、 \( P \) の極座標は \( (\sqrt{2},\frac{3}{4}\pi) \)
極方程式
平面上の曲線が、極座標 \( (r,\theta) \) を用いた式
$$ r=f(\theta) \ または \ F(r,\theta)=0 \tag{2} $$
と表されるとき、式(2)をその曲線の極方程式といいます。
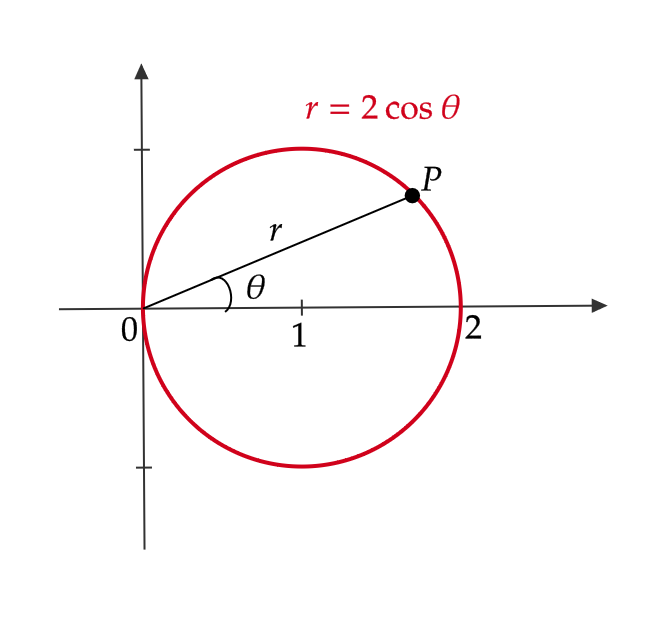
(1) 極方程式 \( r=2\cos\theta \) の表す図形を考える。
両辺に \( r \) をかけると、
$$ r^2=2r\cos\theta $$
\( r^2=x^2+y^2, \ x=r\cos\theta \) より、
$$ x^2+y^2=2x $$
まとめると、
$$ (x-1)^2+y^2=1 $$
よって、中心 \( (1,0) \) 、半径 \( 1 \) の円を表す。
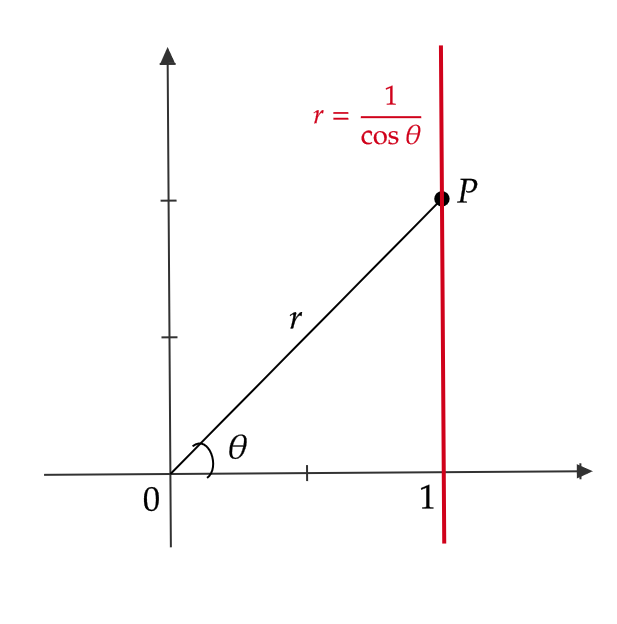
(2) 極方程式 \( r=\frac{1}{\cos\theta} \) の表す図形を考える。
$$ x=r\cos\theta=\frac{\cos\theta}{\cos\theta}=1 $$
$$ y=r\sin\theta=\frac{\sin\theta}{\cos\theta}=\tan\theta $$
より、直線 \( x=1 \) を表す。
2次曲線の極方程式
離心率が \( e \) である2次曲線の極方程式を求めてみましょう。
図のように、原点 \( O \) を1つの焦点にもつ2次曲線の準線を \( \ell \) 、その準線の方程式を \( x=-d \) とします。
曲線上の点を \( P=(r,\theta) \) として、 \( P \) から \( \ell \) に垂線 \( PH \) を下ろします。
このとき、離心率が \( e \) であるので、 \( \frac{PO}{PH}=e \)
よって、
$$ PO=ePH \tag{3} $$
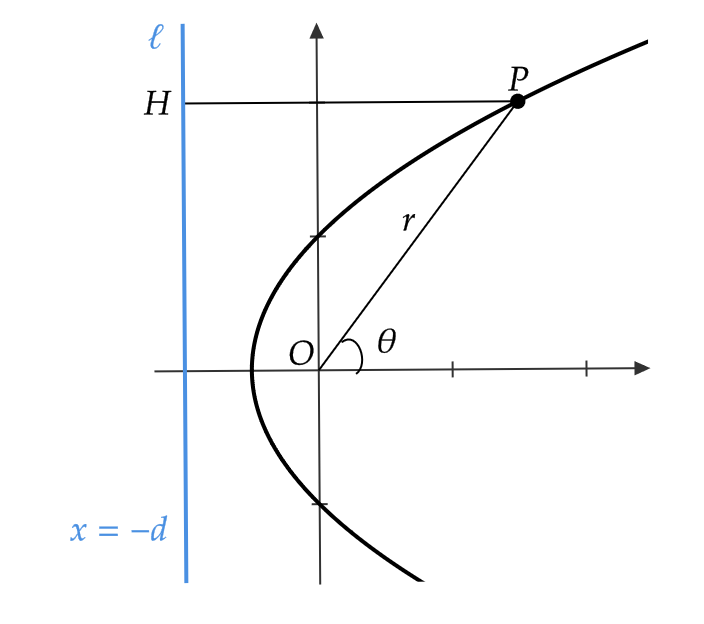
また、 \( PO=r, \ PH=d+r\cos\theta \)
これらを式(3)に代入すると、
$$ r=e(d+r\cos \theta) $$
よって、2次曲線の極方程式は次のようになります。
$$ r=\frac{ed}{1-e\cos\theta} \tag{4} $$
(1) 式(4)において、 \( e=2, \ d=1 \) とすると、
$$ r=\frac{2}{1-2\cos \theta} \tag{5} $$
この極方程式の表す図形を考える。
分母をはらってまとめると、 \( r=2+2r\cos\theta \)
両辺を2乗すると、 \( r^2=(2+2r\cos \theta)^2 \)
ここで、 \( r^2=x^2+y^2, \ x=r\cos\theta \) より
$$ x^2+y^2=(2+2x)^2 $$
まとめると、式(5)は双曲線 \( 9(x+\frac{4}{3})^2-3y^2=4 \) を表す。
(2) 放物線 \( y^2=4x+4 \) を極方程式で表す。
放物線上の点 \( (x,y) \) を極座標 \( (r,\theta) \) で表すと、 \( x=r\cos\theta, \ y=r\sin\theta \) より、
$$ \begin{align} &(r\sin\theta)^2=4r\cos\theta+4 \tag{6} \\ &r^2(1-\cos^2\theta)=4r\cos\theta+4 \\ &r^2=r^2\cos^2\theta+4r\cos\theta+4 \\ &r^2=(r\cos\theta+2)^2 \tag{7} \end{align} $$
まず、式(6)より、 \( 4r\cos\theta+4≧ 0 \) であるので、 \( r\cos\theta+1≧ 0 \)
よって、
$$ r\cos\theta+2=(r\cos\theta+1)+1>0 $$
したがって、 \( r>0, \ r\cos\theta+2>0 \) より、式(7)の両辺の2乗を払うことができて、
$$ r=r\cos\theta+2 $$
\( r \) についてまとめると、求める極方程式は
$$ r=\frac{2}{1-\cos\theta} $$
今回までで高校数学(数学Ⅲ)の内容について特に重要性の高いところを一通り紹介しました。お疲れ様でした。
ここまでの高校数学の知識をもとにして、大学数学も引き続き頑張っていきましょう。
次に勉強するのにおすすめなシリーズとしては、「線形代数学」シリーズもしくは「微分積分学」シリーズとなっています。
それでは、またどこかの記事でお会いしましょう。ひかりでした。

