こんにちは、ひかりです。
今回は高校数学から2次曲線と離心率について解説していきます。
この記事では以下のことを紹介します。
- 放物線・楕円・双曲線の方程式について
- 2次曲線と平行移動について
- 2次曲線と離心率について
放物線・楕円・双曲線の方程式
放物線の方程式
高校数学(数学Ⅲ)01の記事より、2次関数 \( y=ax^2+bx+c \) のグラフは放物線となることを紹介しました。
ここでは、もう少し踏み込んで放物線というものを定義していきます。
放物線とは、1つ固定した点 \( F \) とその点 \( F \) を通らない直線 \( \ell \) から等距離にある点の軌跡のことをいいます。
この点 \( F \) を焦点、直線 \( \ell \) を準線といいます。
\( p\not=0 \) として、焦点 \( F \) を \( (0,p) \) 、準線 \( \ell \) を \( y=-p \) とする放物線を考えると、図のようなグラフとなります。
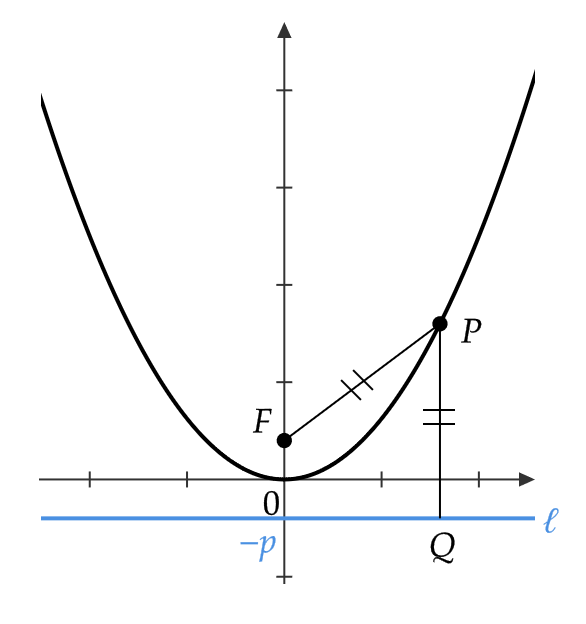
このとき、原点 \( O \) をこの放物線の頂点、 \( y \) 軸をその軸といいます。
この放物線の方程式を求めてみましょう。
放物線上の点 \( P=(x,y) \) から \( \ell \) へと下した垂線を \( PQ \) とすると、放物線の定義より \( |PF|=|PQ| \) であるので、
$$ |PF|=\sqrt{x^2+(y-p)^2}=|x+p|=|PQ| $$
両辺を2乗すると、
$$ x^2+(y-p)^2=(y+p)^2 $$
これを整理すると、
$$ x^2=4py \tag{1} $$
または
$$ y=\frac{1}{4p}x^2 $$
と表すことができます。
まとめると、次のことがいえます。
放物線 \( x^2=4py \) について、次がいえる。
焦点 \( F \) : \( (0,p) \) , 準線 \( \ell \) : \( y=-p \) ,
頂点:原点 \( O \) , 軸: \( y \) 軸 \( (x=0) \) .
式(1)において \( x \) と \( y \) を入れかえた方程式
$$ y^2=4px \tag{2} $$
を考えます。
この方程式は式(1)のグラフの \( x \) 座標と \( y \) 座標を入れかえたものとなるため、図のようなグラフとなります。
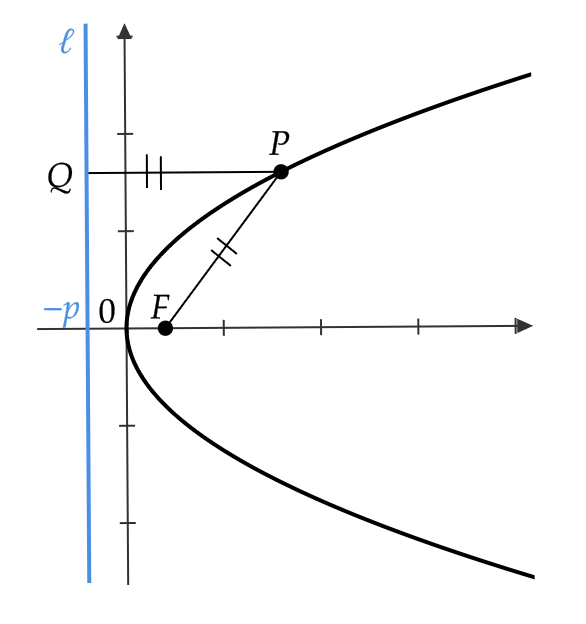
式(1),(2)を放物線の方程式の標準形といいます。
また、式(2)についてまとめると、次のことがいえます。
放物線 \( y^2=4px \) について、次がいえる。
焦点 \( F \) : \( (p,0) \) , 準線 \( \ell \) : \( x=-p \) ,
頂点:原点 \( O \) , 軸: \( x \) 軸 \( (y=0) \) .
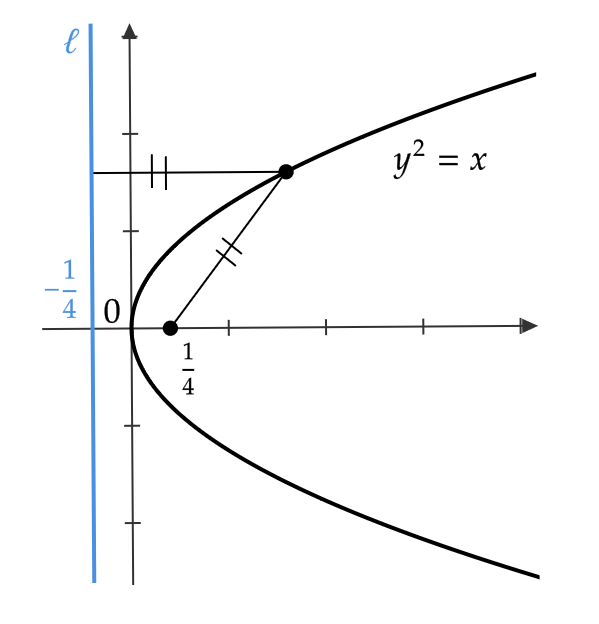
放物線 \( y^2=x \) は \( y^2=4\times \frac{1}{4}x \) と表すことができるので、
焦点は \( \left( \frac{1}{4},0 \right) \)、準線は \( x=-\frac{1}{4} \) となる。
楕円の方程式
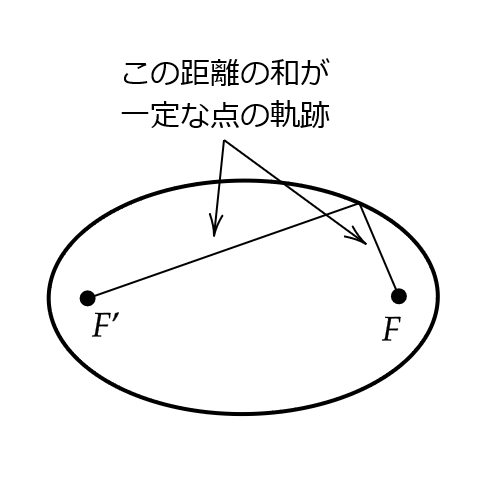
楕円とは、2つの固定した点 \( F,F’ \) からの距離の和が一定である点の軌跡のことをいいます。
このとき、点 \( F,F’ \) をその焦点といいます。
ここで、2点 \( F=(c,0), \ F’=(-c,0) \) を焦点として、2点からの距離の和が \( 2a \) であるような楕円の方程式を求めてみましょう。
ただし、 \( a>c>0 \) とします。
まずグラフとしては、次のようになります。
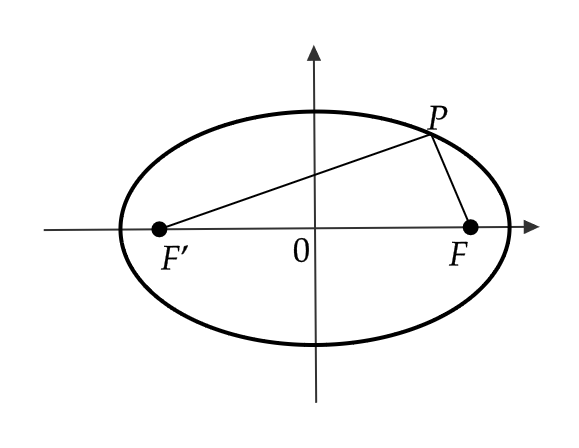
楕円上の点を \( P=(x,y) \) とすると、 \( |PF|+|PF’|=2a \) であるので、
$$ |PF|+|PF’|=\sqrt{(x-c)^2+y^2}+\sqrt{(x+c)^2+y^2}=2a $$
よって、
$$ \sqrt{(x+c)^2+y^2}=2a-\sqrt{(x-c)^2+y^2} $$
両辺を2乗すると、
$$ (x+c)^2+y^2=(2a-\sqrt{(x-c)^2+y^2})^2=4a^2-4a\sqrt{(x-c)^2+y^2}+(x-c)^2+y^2 $$
まとめると、
$$ a\sqrt{(x-c)^2+y^2}=a^2-cx $$
さらに、この両辺を2乗すると、
$$ a^2(x-c)^2+a^2y^2=(a^2-cx)^2=a^4-2a^2cx+c^2x^2 $$
まとめると、
$$ (a^2-c^2)x^2+a^2y^2=a^2(a^2-c^2) $$
ここで、 \( a^2-c^2=b^2, \ b>0 \) とおくと、 \( a>b>0 \) となり、
$$ b^2x^2+a^2y^2=a^2b^2 $$
したがって、
$$ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \tag{3} $$
式(3)を楕円の方程式の標準形といいます。
また、楕円の方程式(3)と \( x \) 軸、 \( y \) 軸との交点
$$ A=(a,0), \ A’=(-a,0), \ B=(0,b), \ B’=(0,-b) $$
を楕円の頂点といい、線分 \( AA’ \) を長軸、線分 \( BB’ \) を短軸といいます。
また、原点 \( O \) を楕円の中心といいます。
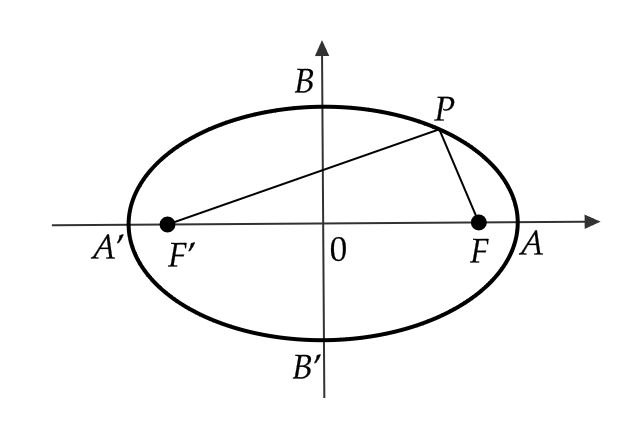
まとめると、次のようになります。
楕円 \( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \) \( (a>b>0) \) について、次がいえる。
焦点 \( F,F’ \): \( (\sqrt{a^2-b^2},0), \ (-\sqrt{a^2-b^2},0) \)
楕円上の点 \( P \) について \( |PF|+|PF’|=2a \)
また、 \( b>a>0 \) のときは、方程式 \( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \) は、 \( y \) 軸上の2点
$$ F=(0,\sqrt{b^2-a^2}), \ F’=(0,-\sqrt{b^2-a^2}) $$
を焦点とする楕円を表します。
このとき、2つの焦点から楕円上の点までの距離の和は \( 2b \) で、線分 \( AA’ \) が短軸、線分 \( BB’ \) が長軸となります。
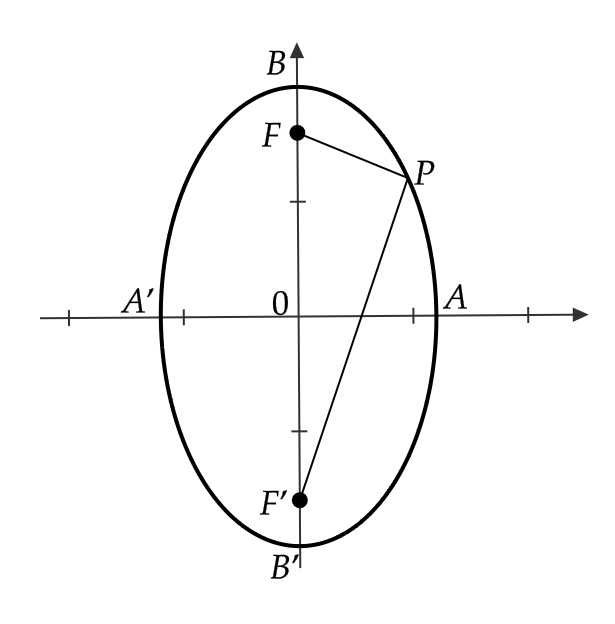
まとめると、次のようになります。
楕円 \( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \) \( (b>a>0) \) について、次がいえる。
焦点 \( F,F’ \): \( (0,\sqrt{b^2-a^2}), \ (0,-\sqrt{b^2-a^2}) \)
楕円上の点 \( P \) について \( |PF|+|PF’|=2b \)
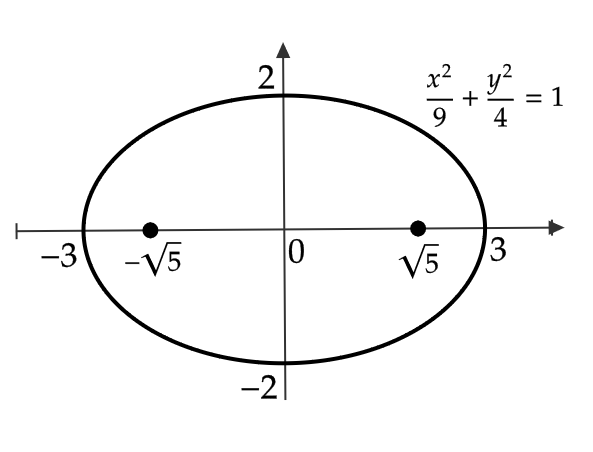
(1) 楕円 \( \frac{x^2}{9}+\frac{y^2}{4}=1 \) の頂点は
$$ (3,0), \ (-3,0), \ (0,2), \ (0,-2) $$
であり、焦点は
$$ (\sqrt{5},0), \ (-\sqrt{5},0) $$
よって、図のようなグラフとなる。
(2) 2点 \( (4,0), \ (-4,0) \) を焦点として、2点からの距離の和が \( 10 \) である楕円の方程式を求める。
求める方程式を \( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \) とおくと、 \( 2a=10, \ \sqrt{a^2-b^2}=4 \) より、 \( a=5, \ b=3 \) となる。
よって、その方程式は \( \frac{x^2}{25}+\frac{y^2}{9}=1 \)
双曲線の方程式
双曲線とは、2つの固定した点 \( F,F’ \) からの距離の差が一定である点の軌跡のことをいいます。
このとき、点 \( F,F’ \) をその焦点といいます。
ここで、2点 \( F=(c,0), \ F’=(-c,0) \) を焦点として、2点からの距離の差が \( 2a \) であるような双曲線の方程式を求めてみましょう。
ただし、 \( c>a>0 \) とします。
まずグラフとしては、次のようになります。
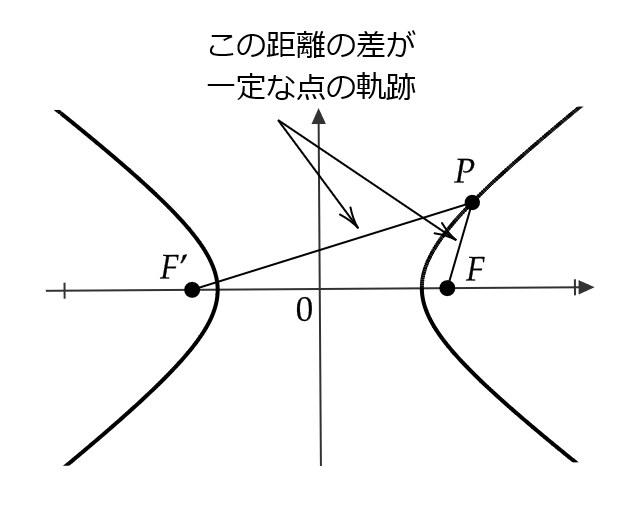
双曲線上の点を \( P=(x,y) \) とすると、 \( | \ |PF|-|PF’| \ |=2a \) であるので、
$$ |PF|-|PF’|=\pm 2a $$
よって、
$$ |PF|-|PF’|=\sqrt{(x-c)^2+y^2}-\sqrt{(x+c)^2+y^2}=\pm 2a $$
したがって、
$$ \sqrt{(x-c)^2+y^2}=\pm 2a+\sqrt{(x+c)^2+y^2} $$
両辺を2乗すると、
$$ (x-c)^2+y^2=(\pm 2a+\sqrt{(x+c)^2+y^2})^2=4a^2\pm 4a\sqrt{(x+c)^2+y^2}+(x+c)^2+y^2 $$
まとめると、
$$ -a^2-cx=\pm a\sqrt{(x+c)^2+y^2} $$
さらに、この両辺を2乗すると、
$$ a^2(x+c)^2+a^2y^2=(-a^2-cx)^2=a^4+2a^2cx+c^2x^2 $$
まとめると、
$$ (c^2-a^2)x^2-a^2y^2=a^2(c^2-a^2) $$
ここで、 \( c^2-a^2=b^2, \ b>0 \) とおくと、
$$ b^2x^2-a^2y^2=a^2b^2 $$
したがって、
$$ \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \tag{4} $$
式(4)を双曲線の方程式の標準形といいます。
また、双曲線の方程式(4)と \( x \) 軸との交点
$$ A=(a,0), \ A’=(-a,0) $$
を双曲線の頂点といい、直線 \( AA’ \) を主軸といいます。
また、原点 \( O \) を双曲線の中心といいます。
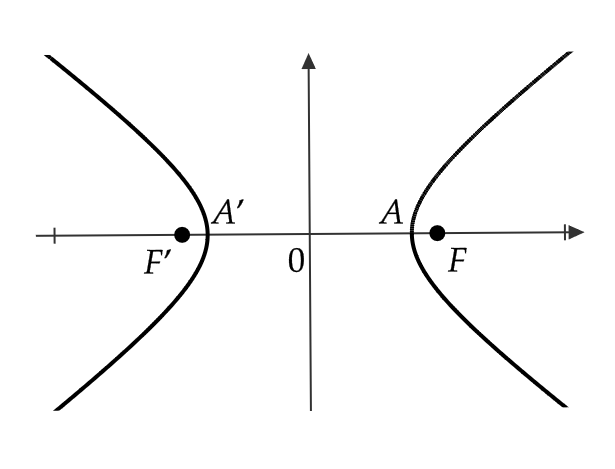
まとめると、次のようになります。
双曲線 \( \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \ (a>0, \ b>0) \) について、次がいえる。
焦点 \( F,F’ \): \( (\sqrt{a^2+b^2},0), \ (-\sqrt{a^2+b^2},0) \)
双曲線上の点 \( P \) について \( | \ |PF|-|PF’| \ |=2a \)
式(4)において \( x \) と \( y \) および \( a \) と \( b \) を入れかえた方程式
$$ \frac{y^2}{b^2}-\frac{x^2}{a^2}=1 \quad すなわち \quad \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1 $$
を考えます。
これは、 \( y \) 軸上の2点
$$ F=(0,\sqrt{a^2+b^2}), \ F’=(0,-\sqrt{a^2+b^2}) $$
を焦点とする双曲線を表します。
この双曲線の頂点は
$$ B=(0,b), \ B’=(0,-b) $$
であり、2つの焦点からの距離の差は \( 2b \) となります。
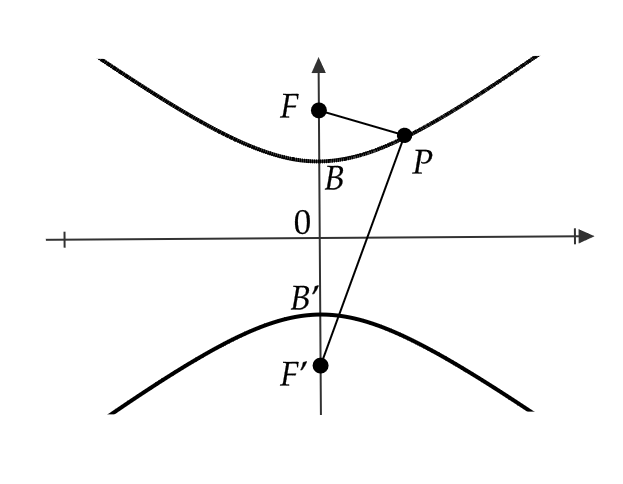
まとめると、次のようになります。
双曲線 \( \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1 \ (a>0, \ b>0) \) について、次がいえる。
焦点 \( F,F’ \): \( (0,\sqrt{a^2+b^2}), \ (0,-\sqrt{a^2+b^2}) \)
双曲線上の点 \( P \) について \( | \ |PF|-|PF’| \ |=2b \)
(1) 双曲線 \( \frac{x^2}{16}-\frac{y^2}{9}=1 \) の頂点は
$$ (4,0), \ (-4,0), $$
であり、焦点は
$$ (5,0), \ (-5,0) $$
よって、図のようなグラフとなる。
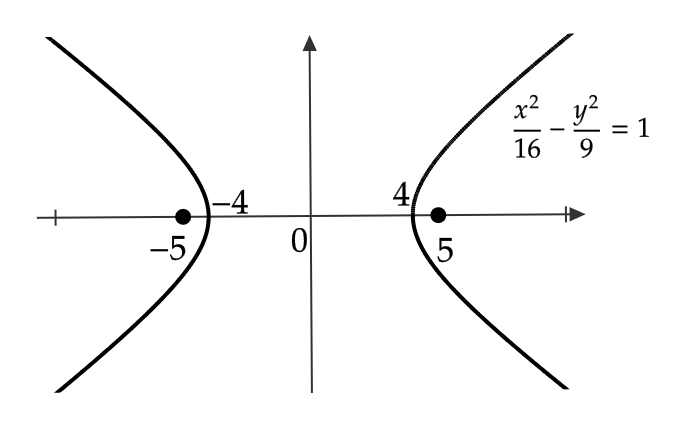
(2) 2点 \( (4,0), \ (-4,0) \) を焦点として、2点からの距離の差が \( 6 \) である双曲線の方程式を求める。
求める方程式を \( \frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \) とおくと、 \( 2a=6, \ \sqrt{a^2+b^2}=4 \) より、 \( a=3, \ b=\sqrt{7} \) となる。
よって、その方程式は \( \frac{x^2}{9}-\frac{y^2}{7}=1 \)
放物線 \( y^2=4px \) 、楕円 \( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 \) 、双曲線 \( \frac{x^2}{a^2}-\frac{y^2}{b^2}=\pm 1 \) は、いずれも \( x,y \) についての2次方程式で表されています。
よって、これらの曲線をまとめて、2次曲線といいます。
2次曲線と平行移動
放物線、楕円、双曲線などは、いずれも \( x, \ y \) についての方程式
$$ f(x,y)=0 \tag{5} $$
の形で表されます。
ここで、式(5)で表された図形 \( F \) を、 \( x \) 軸方向に \( m \) 、 \( y \) 軸方向に \( n \) だけ平行移動した図形 \( G \) の方程式を考えてみましょう。
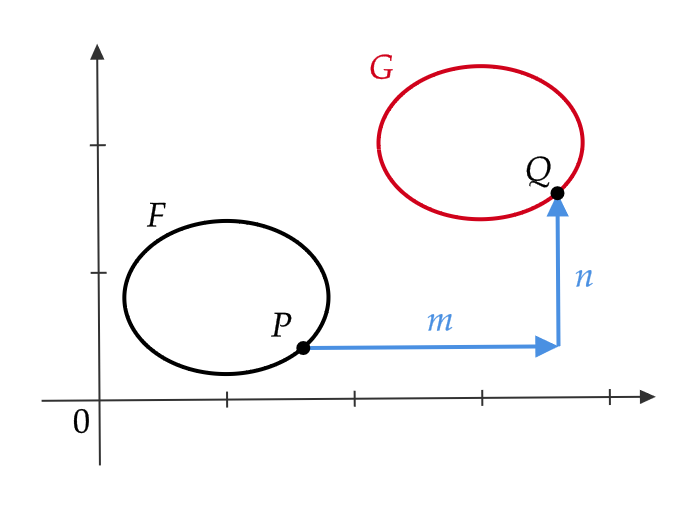
\( F \) 上の点 \( P \) がこの平行移動によって \( G \) 上の点 \( Q \) に移るとします。
\( P, \ Q \) の座標をそれぞれ \( (u,v), \ (x,y) \) とすると、式(1)より \( (u,v) \) は \( f(u,v)=0 \) をみたし、
\( \begin{cases} x=u+m \\ y=v+n \end{cases} \) すなわち、 \( \begin{cases} u=x-m \\ v=y-n \end{cases} \) となるので、
$$ f(x-m,y-n)=0 \tag{6} $$
ここで、式(6)が図形 \( G \) の方程式となります。
まとめると、次が成り立ちます。
方程式 \( f(x,y)=0 \) で表される図形 \( F \) を、 \( x \) 軸方向に \( m \) 、 \( y \) 軸方向に \( n \) だけ平行移動した図形 \( G \) の方程式は
$$ f(x-m,y-n)=0 $$
(1) 方程式 \( \frac{(x-2)^2}{4}+(y-1)^2=1 \) は、楕円 \( \frac{x^2}{4}+y^2=1 \) を \( x \) 軸方向に \( 2 \) 、 \( y \) 軸方向に \( 1 \) だけ平行移動した楕円を表す。
(2) 方程式 \( \frac{(x-1)^2}{4}-\frac{(y+2)^2}{9}=1 \) は、双曲線 \( \frac{x^2}{4}-\frac{y^2}{9}=1 \) を \( x \) 軸方向に \( 1 \) 、 \( y \) 軸方向に \( -2 \) だけ平行移動した双曲線を表す。
(3) 2次関数 \( y=a(x-m)^2+n \) は、放物線 \( y=ax^2 \) を \( x \) 軸方向に \( m \) 、 \( y \) 軸方向に \( n \) だけ平行移動した放物線を表す。
2次曲線と離心率
2次曲線を分類する1つの方法として離心率を用いた方法があるため、簡単に紹介していきます。
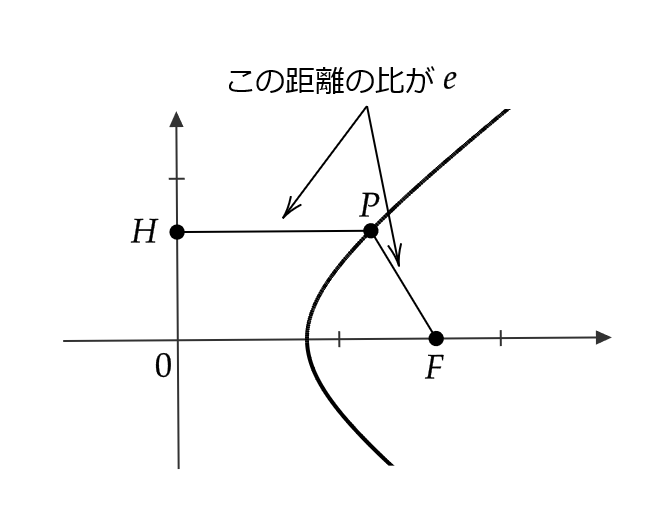
1つの固定した点 \( F \) と固定した直線 \( \ell \) への距離の比の値 \( e \) が一定である点 \( P \) の軌跡について、次のことが成り立つことが知られています。
定点 \( F \) と定直線 \( \ell \) への距離の比の値 \( e \) が一定である点 \( P \) の軌跡は、 \( F \) を1つの焦点とする2次曲線であり、
\( 0<e<1 \) のとき:楕円
\( e=1 \) のとき:放物線
\( e>1 \) のとき:双曲線
である。この \( e \) の値を2次曲線の離心率といい、直線 \( \ell \) を準線という。
点 \( F=(3,0) \) と \( y \) 軸への距離の比の値が \( e \) である点を \( P=(x,y) \) とするとき、 \( e \) の値によって点 \( P \) の軌跡がどのように変化するかを調べる。
点 \( P \) から \( y \) 軸までの距離を \( |PH| \) とおくと、
$$ \frac{|PF|}{|PH|}=e $$
ここで、
$$ |PF|=\sqrt{(x-3)^2+y^2}, \quad |PH|=|x| $$
であるので、
$$ \sqrt{(x-3)^2+y^2}=e|x| $$
両辺を2乗すると、
$$ (x-3)^2+y^2=e^2x^2 $$
まとめると、
$$ y^2=(e^2-1)x^2+6x-9 \tag{7} $$
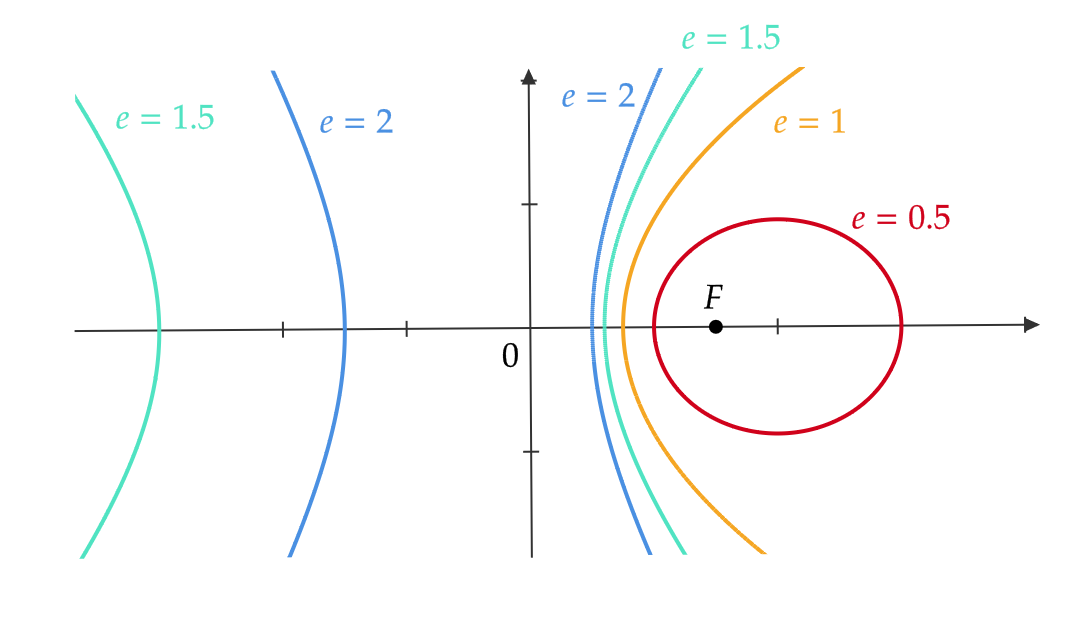
式(7)に \( e=0.5, \ e=1, \ e=1.5, \ e=2 \) を代入した式の表す2次曲線の概形をかくと、次のようになる。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

