こんにちは、ひかりです。
今回は高校数学から積分による面積・体積の求め方について解説していきます。
定積分については前回の記事をご覧ください。
この記事では以下のことを紹介します。
- 積分による面積の求め方について
- 積分による体積の求め方について
積分による面積の求め方
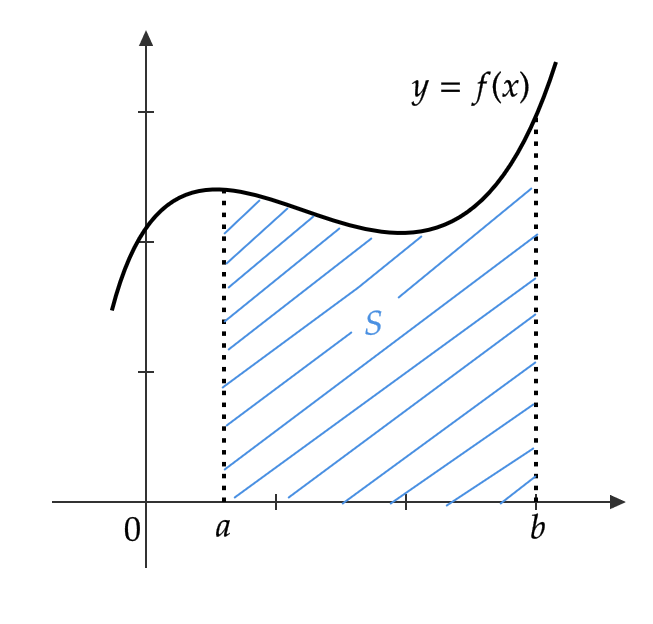
曲線とx軸との面積
区間 \( [a,b] \) において、 \( f(x)≧ 0 \) であるとき、曲線 \( y=f(x) \) と \( x \) 軸および \( x=a, \ x=b \) で囲まれた図形の面積 \( S \) は、前回の記事より次で与えられていました。
$$ S=\int_a^bf(x)dx $$
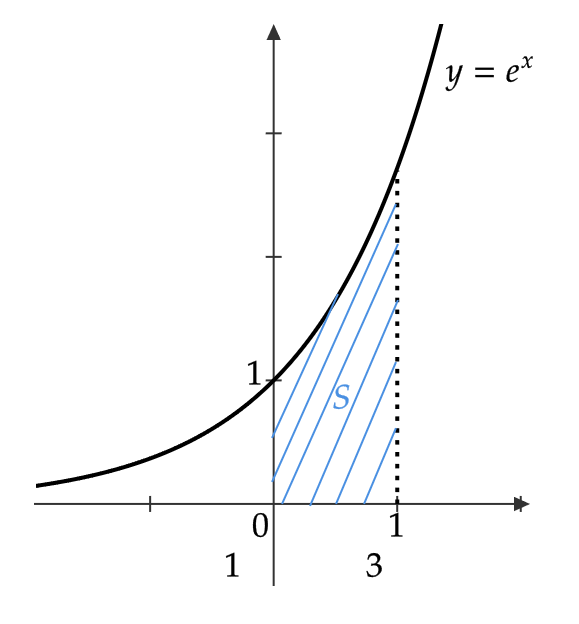
\( y=e^x \) 、 \( x \) 軸、 \( y \) 軸、 \( x=1 \) で囲まれた図形の面積 \( S \) は
$$ S=\int_0^1e^xdx=[e^x]^1_0=e-1 $$
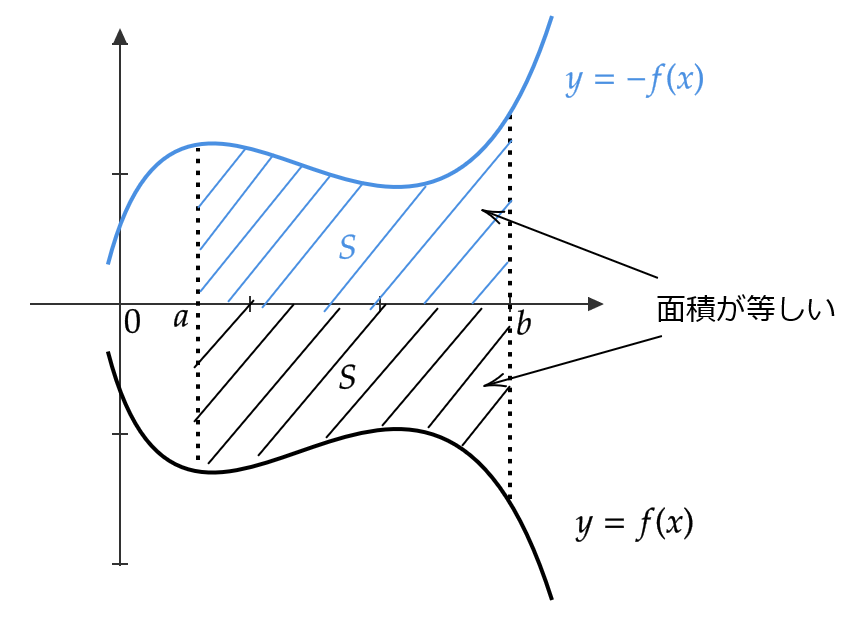
\( f(x)≦ 0 \) のときは \( f(x) \) と \( -f(x) \) が \( x \) 軸に関して対称であることより、 \( -f(x)≧0 \) での面積を求めれば \( f(x) \) での面積を求めることができます。つまり、
$$ S=\int_a^b\{ -f(x) \}dx=-\int_a^bf(x)dx $$
\( y=-x^2+1 \) 、 \( x \) 軸、 \( x=2 \) で囲まれた図形の面積 \( S \) を求める。
\( -1≦ x≦ 1 \) のとき \( -x^2+1≧ 0 \)
\( 1≦ x≦ 2 \) のとき \( -x^2+1≦ 0 \)
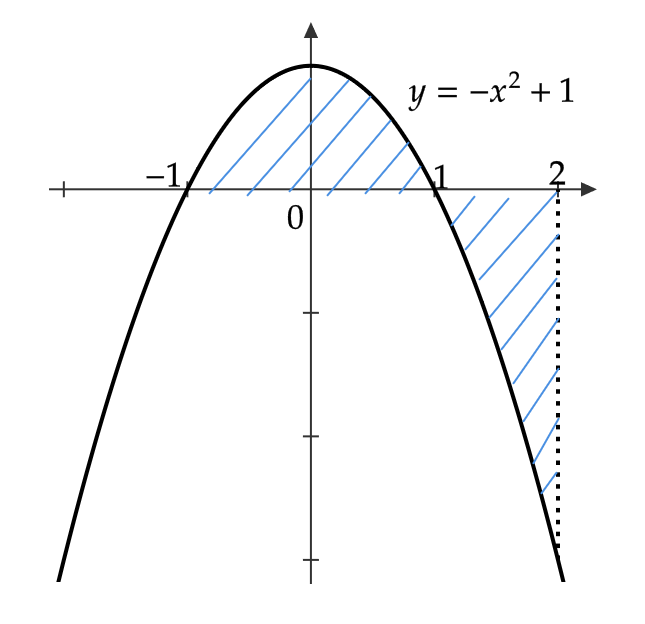
よって、
$$ \begin{align} S&=\int_{-1}^1(-x^2+1)dx-\int_1^2(-x^2+1)dx \\ &=\left[ -\frac{1}{3}x^3+x\right]^1_{-1}-\left[ -\frac{1}{3}x^3+x \right]^2_1=\frac{8}{3} \end{align} $$
2曲線間の面積
2つの曲線 \( y=f(x), \ y=g(x) \) が区間 \( a≦ x≦ b \) において、 \( f(x)≧ g(x) \) とします。
このとき、 \( y=f(x), \ y=g(x), \ x=a, \ x=b \) で囲まれた図形の面積 \( S \) を求めます。
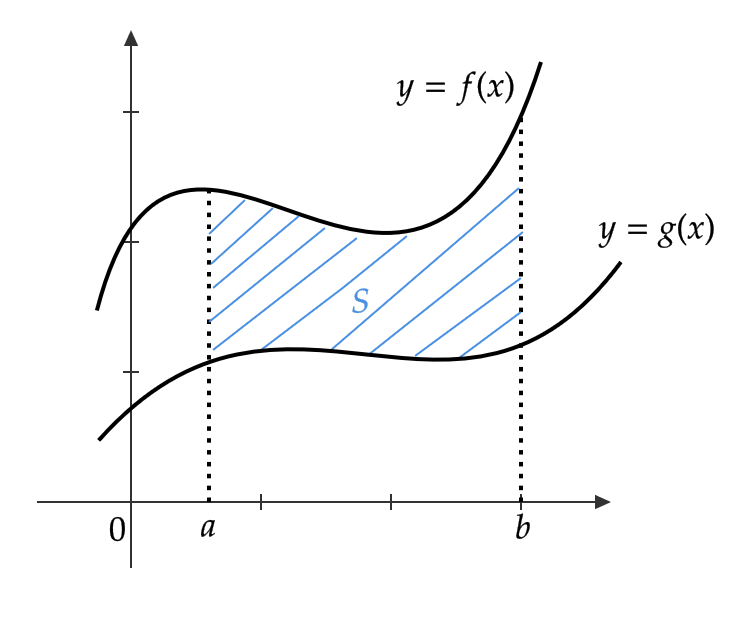
まず、 \( f(x)≧ g(x) ≧ 0 \) とすると、
$$ S=\int_a^bf(x)dx-\int_a^bg(x)dx=\int_a^b\{ f(x)-g(x) \}dx $$
また、 \( f(x)≧ g(x)≧ 0 \) とは限らないときは、 \( g(x)+m≧ 0 \) となるような \( m \) をとることで、
$$ f(x)+m≧ g(x)+m ≧ 0 $$
となります。
これは、 \( f(x), \ g(x) \) を上に \( m \) だけ平行移動させることに対応しています。
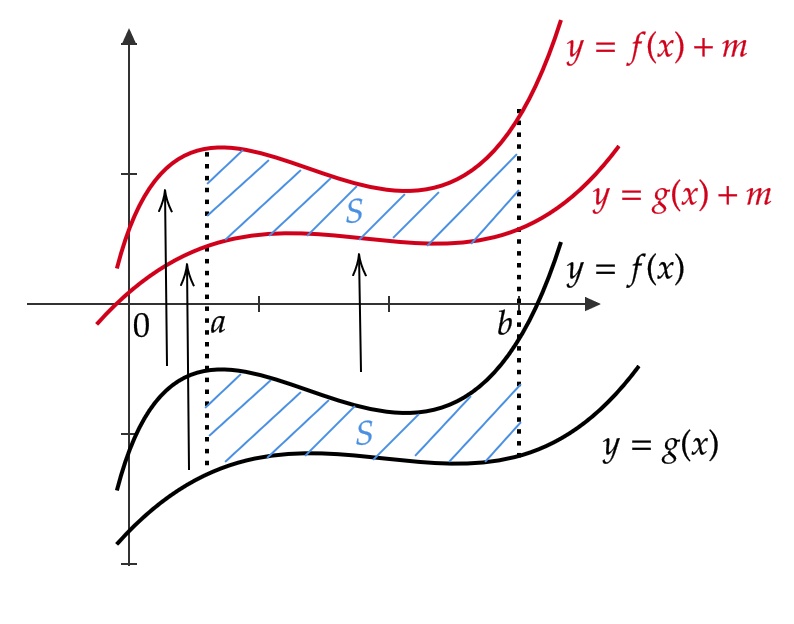
すると、
$$ \begin{align} S&=\int_a^b\{ f(x)+m \} dx-\int_a^b \{ g(x)+m \} dx \\ &=\int_a^b\{ f(x)-g(x) \} dx \end{align} $$
よって、まとめると次が成り立ちます。
区間 \( a≦ x≦ b \) において、 \( f(x)≧ g(x) \) であるとき、 \( y=f(x), \ y=g(x), \ x=a, \ x=b \) で囲まれた図形の面積 \( S \) は、
$$ S=\int_a^b\{ f(x)-g(x) \} dx $$
(1) \( y=x^2-2x, \ y=-x^2+4 \) で囲まれた図形の面積 \( S \) を求める。
まず、 \( y=x^2-2x, \ y=-x^2+4 \) の交点は
$$ x^2-2x=-x^2+4 $$
の実数解 \( x=-1,2 \) である。
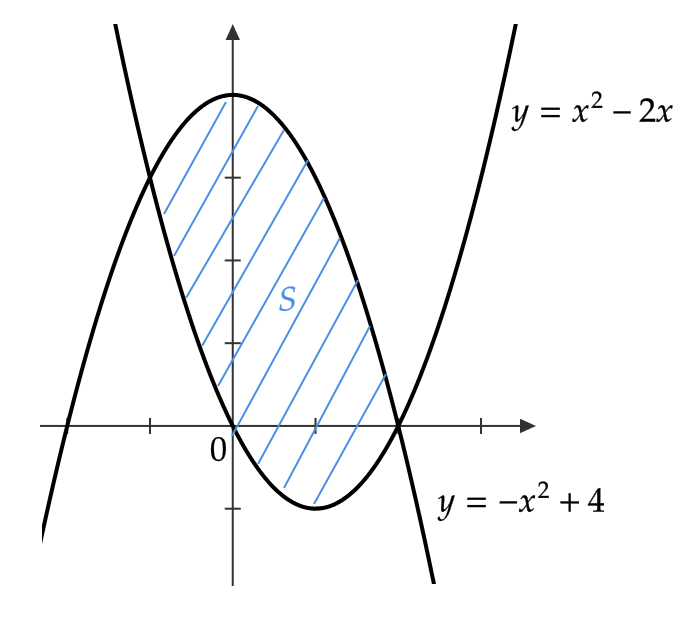
区間 \( -1≦ x≦ 2 \) では
$$ -x^2+4≧ x^2-2x $$
であるので、
$$ \begin{align} S&=\int_{-1}^2\{ (-x^2+4)-(x^2-2x)\} dx \\ &=\int_{-1}^2(-2x^2+2x+4)dx \\ &=\left[ -\frac{2}{3}x^3+x^2+4x \right]^2_{-1}=9 \end{align} $$
(2) 円 \( x^2+y^2=1 \) で囲まれた図形の面積 \( S \) を求める。
\( x^2+y^2=1 \) を \( y \) について解くと、 \( y^2=1-x^2 \) より、
$$ y=\pm\sqrt{1-x^2} $$
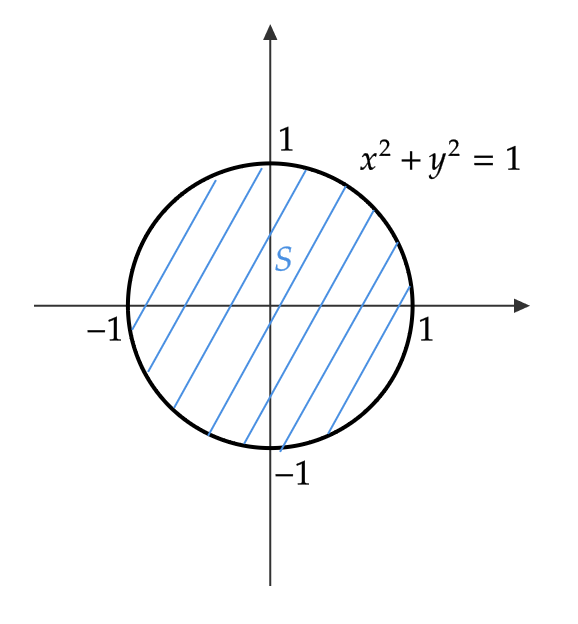
このとき、\( y=\sqrt{1-x^2} \) が円の上半分、 \( y=-\sqrt{1-x^2} \) が円の下半分を表している。
よって、
$$ \begin{align} S&=\int_{-1}^1\{\sqrt{1-x^2}-(-\sqrt{1-x^2}) \}dx \\ &=2\int_{-1}^1\sqrt{1-x^2}dx=(*) \end{align} $$
\( x=\sin \theta \) とおくと、 \( \frac{dx}{d\theta}=\cos \theta \)
また、
| \( x \) | \( -1 \quad \to \quad 1 \) |
| \( \theta \) | \( -\frac{\pi}{2} \quad \to \frac{\pi}{2} \) |
さらに、加法定理より、
$$ \begin{align} \cos 2\theta&=\cos (\theta+\theta)=\cos\theta\cos\theta-\sin\theta\sin\theta \\ &=\cos^2\theta-\sin^2\theta=\cos^2\theta-(1-\cos^2\theta) \\ &=1+2\cos^2\theta \end{align} $$
よって、
$$ \begin{align} (*)&=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{1-\sin^2\theta}\cos\theta d\theta \\ &=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^2\theta d\theta=2\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1+\cos 2\theta}{2}d\theta \\ &=\left[ \theta+\frac{1}{2}\sin 2\theta \right]^{\frac{\pi}{2}}_{-\frac{\pi}{2}}=\left( \frac{\pi}{2}+\frac{1}{2}\sin \pi \right)-\left( -\frac{\pi}{2}+\frac{1}{2}\sin (-\pi) \right) \\ &=\pi \end{align} $$
これは円の面積の公式 \( \pi r^2 \) で \( r=1 \) としたときと同じとなる。
積分による体積の求め方
ある立体の \( x \) 軸に垂直な2平面 \( A,B \) の間に挟まれた部分の体積 \( V \) を求めることを考えます。
\( x \) 軸との座標が \( x \) の点で垂直に交わる平面 \( X \) でこの立体を切ったときの切り口の面積を \( S(x) \) とします。
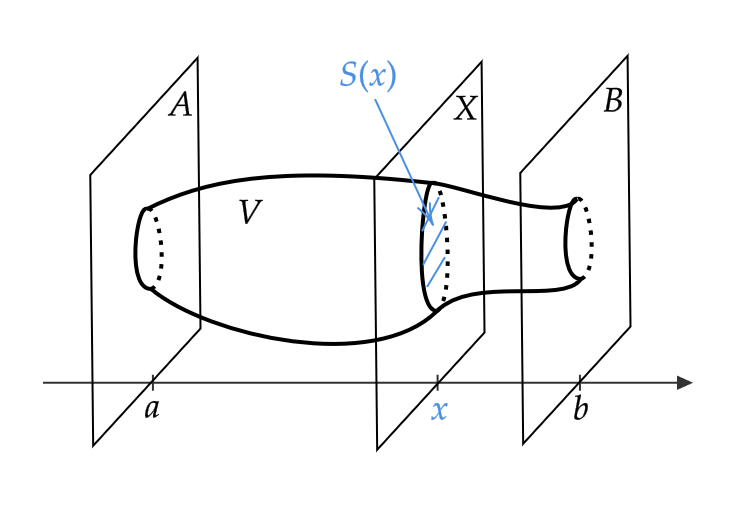
このとき、前回の記事で紹介した議論と同様にして、次が成り立ちます。
$$ V=\int_a^b S(x)dx $$
特に、曲線 \( y=f(x) \) と \( x \) 軸および、 \( x=a, \ x=b \) で囲まれた図形を \( x \) 軸まわりに1回転したときの回転体の体積を考えてみましょう。
このとき、 \( S(x) \) は半径 \( f(x) \) の円の面積なので、 \( S(x)=\pi\{f(x)\}^2 \) となります。
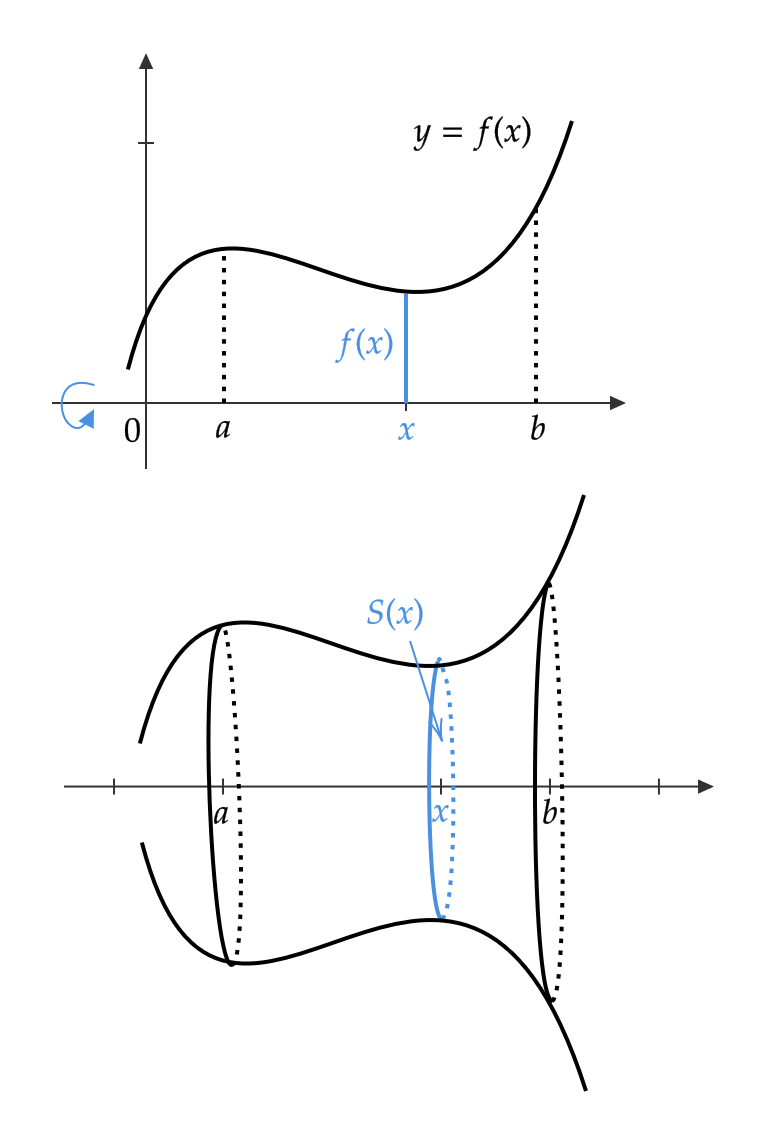
よって、次が成り立ちます。
$$ V=\pi\int_a^b\{ f(x)\}^2dx $$
半径 \( r \) の球の体積を求める。
半径 \( r \) の球は区間 \( -r≦ x≦ r \) において、半円 \( y=\sqrt{r^2-x^2} \) が \( x \) 軸のまわりに1回転した回転体となる。
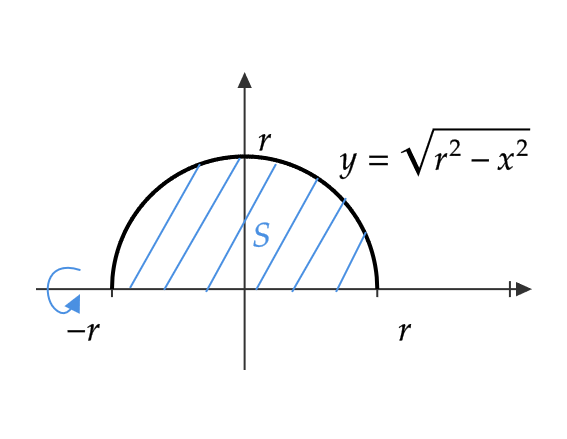
よって、
$$ V=\pi\int_{-r}^r(r^2-x^2)dx=\pi\left[ r^2x-\frac{1}{3}x^3 \right]^r_{-r}=\frac{4}{3}\pi r^3 $$
これは球の体積の公式と同じとなる。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

