こんにちは、ひかりです。
今回は高校数学から微分係数と導関数の定義について解説していきます。
この記事では以下のことを紹介します。
- 微分係数について
- 微分可能性と連続性の関係について
- 導関数とその性質について
微分係数
微分係数と微分可能性
関数 \( y=f(x) \) に対して、 \( x \) の値が \( a \) から \( b \) まで変化するとき、 \( x \) の変化量 \( b-a \) と \( y \) の変化量 \( f(b)-f(a) \) との比の値
$$ \frac{f(b)-f(a)}{b-a} \tag{1} $$
を \( x \) が \( a \) から \( b \) まで変わるときの関数 \( y=f(x) \) の平均変化率といいます。
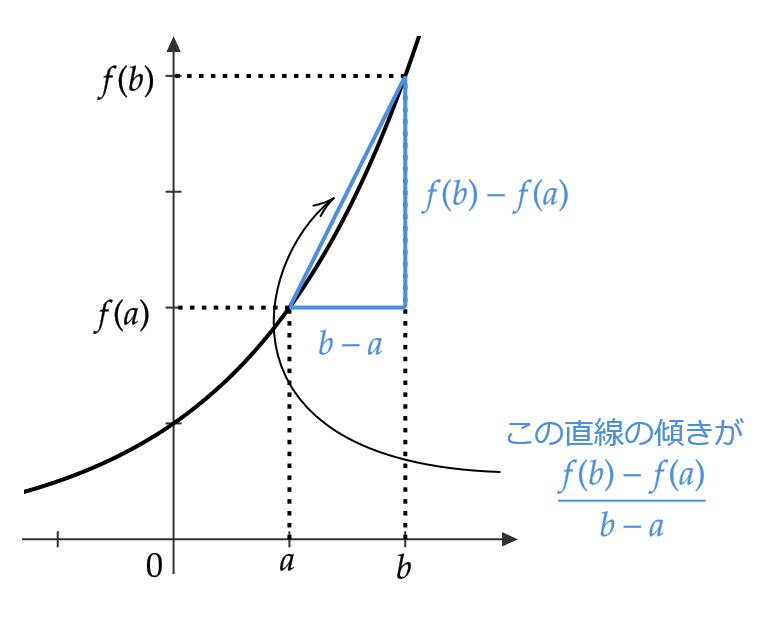
\( f(x)=x^2 \) に対して、
(1) \( x \) が \( 1 \) から \( 2 \) まで変わるときの平均変化率
$$ \frac{f(2)-f(1)}{2-1}=\frac{2^2-1^2}{2-1}=3 $$
(2) \( x \) が \( -2 \) から \( 0 \) まで変わるときの平均変化率
$$ \frac{f(0)-f(-2)}{0-(-2)}=\frac{0^2-(-2)^2}{0-(-2)}=-2 $$
式(1)において、 \( b \) を \( a+h \) で置き換えると、次が成り立ちます。
$$ \frac{f(a+h)-f(a)}{(a+h)-a}=\frac{f(a+h)-f(a)}{h}, \quad (h\not=0) $$
\( f(x)=x^2+3x \) に対して、 \( x \) が \( 2 \) から \( 2+h \) まで変わるときの平均変化率は
$$ \begin{align} \frac{f(2+h)-f(2)}{h}&=\frac{\{(2+h)^2+3(2+h)\}-(2^2+3\times 2)}{h} \\ &=\frac{(4+4h+h^2+6+3h)-10}{h}=\frac{h^2+7h}{h}=7+h \end{align} $$
ここで、 \( x \) が \( a \) から \( a+h \) まで変わるときの平均変化率 \( \frac{f(a+h)-f(a)}{h} \) において、 \( h \) を限りなく \( 0 \) に近づけることを考えます。
\( \displaystyle \lim_{h\to0}\frac{f(a+h)-f(a)}{h} \) を関数 \( y=f(x) \) の \( x=a \) における微分係数といい、 \( f'(a) \) で表す。
また、このとき \( f(x) \) は \( x=a \) で微分可能であるという。
\( f(x)=x^2 \) に対して、
(1) \( x=1 \) における微分係数
$$ \begin{align} f'(1)&=\lim_{h\to0}\frac{f(1+h)-f(1)}{h}=\lim_{h\to0}\frac{(1+h)^2-1^2}{h} \\ &=\lim_{h\to0}\frac{1+2h+h^2-1}{h}=\lim_{h\to0}\frac{h^2+2h}{h} \\ &=\lim_{h\to0}(2+h)=2 \end{align} $$
(2) \( x=a \) における微分係数
$$ \begin{align} f'(a)&=\lim_{h\to0}\frac{f(a+h)-f(a)}{h}=\lim_{h\to0}\frac{(a+h)^2-a^2}{h} \\ &=\lim_{h\to0}(2a+h)=2a \end{align} $$
微分係数の図形的意味
\( \displaystyle \frac{f(a+h)-f(a)}{h} \) は関数 \( y=f(x) \) の点 \( A=(a,f(a)) \) と \( B=(a+h,f(a+h)) \) を結ぶ直線の傾きとなります。
なぜならば、この直線を \( y=\alpha x+\beta \) とおいて、点 \( A=(a,f(a)) \) と点 \( B=(a+h,f(a+h)) \) を代入すると、
$$ f(a)=\alpha a+\beta \tag{2} $$
$$ f(a+h)=\alpha (a+h)+\beta \tag{3} $$
式(3)-式(2)をすると、
$$ f(a+h)-f(a)=\alpha \{(a+h)-a\} $$
よって、傾き \( \alpha \) は
$$ \alpha=\frac{f(a+h)-f(a)}{h} $$
となります。
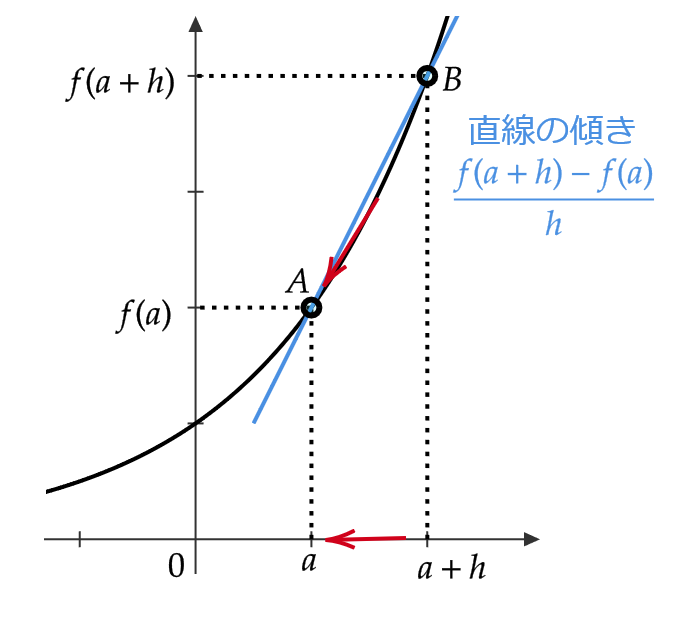
これを \( h\to0 \) とすると、点 \( B \) は点 \( A \) に限りなく近づきます。
よって、 \( f'(a) \) は \( y=f(x) \) の点 \( (a,f(a)) \) における接線の傾きに等しいことがわかります。
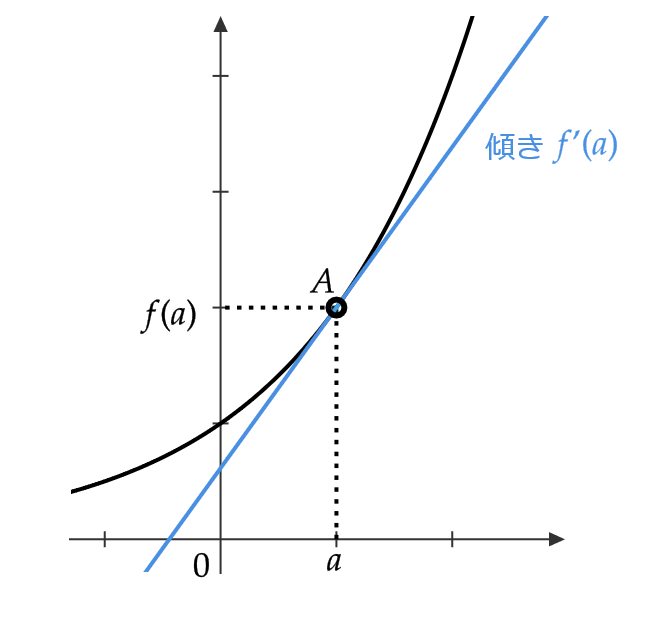
微分可能性と連続性
関数 \( f(x) \) が \( x=a \) で微分可能ならば、 \( f'(a) \) が存在します。よって、
$$ \begin{align} \lim_{x\to a}\{ f(x)-f(a)\}&=\lim_{x\to a}\left\{ (x-a)\cdot \frac{f(x)-f(a)}{x-a} \right\} \\ &=0\times f'(a)=0 \end{align} $$
よって、 \( \displaystyle \lim_{x\to a}f(x)=f(a) \) なので、次が成り立ちます。
関数 \( f(x) \) が \( x=a \) で微分可能ならば、 \( f(x) \) は \( x=a \) において連続となる。
ただし、逆は成り立ちません。すなわち、
関数 \( f(x) \) が \( x=a \) において連続であっても、 \( f(x) \) は \( x=a \) で微分可能であるとは限らない。
\( f(x)=|x| \) は \( x=0 \) において連続である。しかし、
$$ \begin{align} \lim_{h\to +0}\frac{f(0+h)-f(0)}{h}&=\lim_{h\to +0}\frac{|h|}{h}=\lim_{h\to +0}\frac{h}{h} \\ &=\lim_{h\to +0}1=1 \end{align} $$
$$ \begin{align} \lim_{h\to -0}\frac{f(0+h)-f(0)}{h}&=\lim_{h\to -0}\frac{|h|}{h}=\lim_{h\to -0}\frac{-h}{h}=-1 \end{align} $$
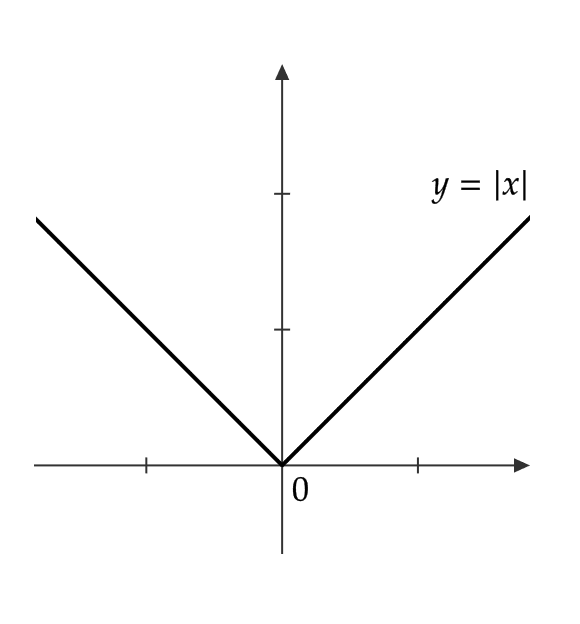
よって、 \( \displaystyle \lim_{h\to 0}\frac{f(0+h)-f(0)}{h} \) は存在しない。
つまり、 \( x=0 \) で微分可能ではない。
導関数とその性質
導関数の定義
まず、微分係数をもとにして導関数というものを定義します。
関数 \( y=f(x) \) に対して、 \( x \) に \( f'(x) \) を対応させて得られる関数を \( f(x) \) の導関数といい、 \( f'(x), \ y’, \ \frac{dy}{dx} \) などと書く。つまり、
$$ f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h} $$
また、関数の導関数を求めることを、関数を微分するという。
(1) \( f(x)=x \) を微分する。
$$ f'(x)=\lim_{h\to0}{(x+h)-x}{h}=\lim_{h\to 0}\frac{h}{h}=1 $$
(2) \( f(x)=\frac{1}{x} \) を微分する。
$$ \begin{align} f'(x)&=\lim_{h\to 0}\frac{\frac{1}{x+h}-\frac{1}{x}}{h}=\lim_{h\to0}\frac{\frac{x-(x+h)}{x(x+h)}}{h} \\ &=\lim_{h\to 0}\frac{\frac{-h}{x(x+h)}}{h}=\lim_{h\to0}\frac{-1}{x(x+h)}=-\frac{1}{x^2} \end{align} $$
(3) \( f(x)=\sqrt{x} \) を微分する。
$$ \begin{align} f'(x)&= \lim_{h\to0}\frac{\sqrt{x+h}-\sqrt{x}}{h}=\lim_{h\to0}\frac{(\sqrt{x+h}-\sqrt{x})(\sqrt{x+h}+\sqrt{x})}{h(\sqrt{x+h}+\sqrt{x})} \\ &=\lim_{h\to0}\frac{(x+h)-x}{h(\sqrt{x+h}+\sqrt{x})}=\lim_{h\to0}\frac{1}{\sqrt{x+h}+\sqrt{x}}=\frac{1}{2\sqrt{x}} \end{align} $$
\( x^n \) の導関数
\( n \) を正の整数とすると、二項定理より、
$$ \begin{align} (x+h)^n&=x^n+{}_nC_1x^{n-1}h+{}_nC_2x^{n-2}h^2+\cdots+{}_nC_{n-1}xh^{n-1}+h^n \\ &=x^n+nx^{n-1}h+\frac{n(n-1)}{2}x^{n-2}h^2+\cdots+nxh^{n-1}+h^n \end{align} $$
よって、
$$ \frac{(x+h)^n-x^n}{h}=nx^{n-1}+\frac{n(n-1)}{2}x^{n-2}h+\cdots+nxh^{n-2}+h^{n-1} $$
したがって、
$$ (x^n)’=\lim_{h\to0}\frac{(x+h)^n-x^n}{h}=nx^{n-1} $$
\( n \) が正の整数のとき、 \( (x^n)’=nx^{n-1} \)
(1) \( (x^2)’=2x \)
(2) \( (x^4)’=4x^3 \)
(3) \( (x^{10})’=10x^9 \)
導関数の性質
\( f(x), \ g(x) \) が微分可能な関数のとき、
(1) \( (c)’=0, \quad (c:\text{定数}) \)
(2) \( \{ kf(x)\}’=kf'(x), \quad (k:\text{定数}) \)
(3) \( \{ f(x)+g(x) \}’=f'(x)+g'(x) \)
(4) \( \{ f(x)-g(x) \}’=f'(x)-g'(x) \)
\( y=2x^7+5x^3-18x+15 \) を考えると、
$$ y’=2\cdot 7x^6+5\cdot 3x^2-18=14x^6+15x^2-18 $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

