こんにちは、ひかりです。
今回は高校数学から関数の連続性について解説していきます。
関数の極限について知りたい方は前回の記事をご覧ください。
この記事では以下のことを紹介します。
- 関数の連続性について
- 連続関数の最大値・最小値について
- 中間値の定理について
関数の連続性
\( x=a \) での連続性
いままで学んできた関数では、 \( y=x^2 \) や \( y=\sin x \) のように、そのグラフが1つのつながった曲線になるものが多かったです。
このような関数 \( f(x) \) では、 \( \displaystyle \lim_{x\to a}f(x)=f(a) \) が成り立ちます。
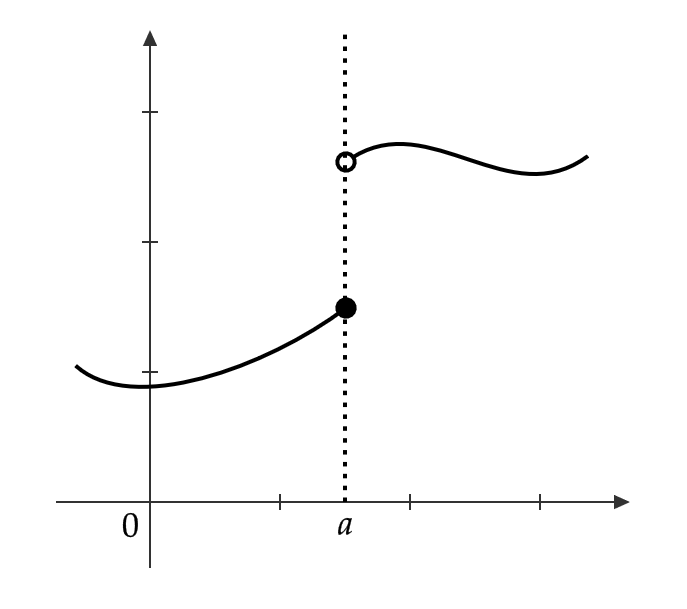
しかし、関数のグラフが次のように途切れている場合には \( \displaystyle \lim_{x\to a}f(x) \) は存在しません。
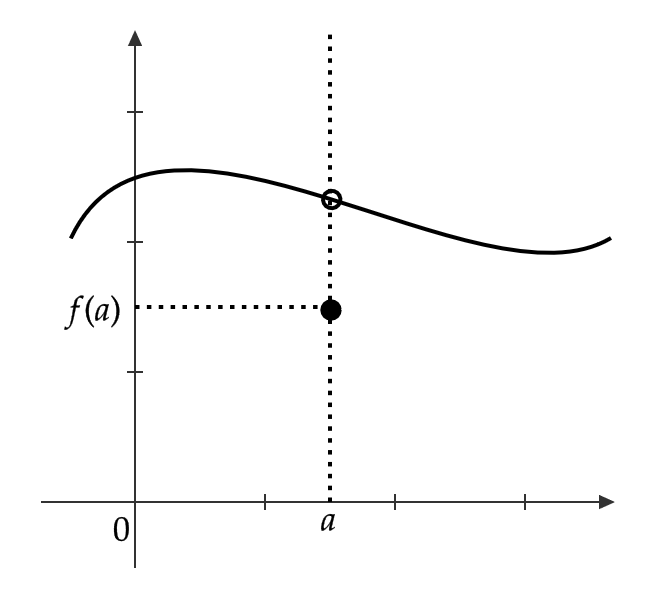
また、関数のグラフが次のように点 \( a \) でずれているような場合には \( \displaystyle \lim_{x\to a}f(x) \) は存在するが、 \( f(a) \) とはなりません。
これらの考察をもとに、関数が点 \( x=a \) で連続であることを次で定めます。
関数 \( f(x) \) が \( x=a \) で連続であるとは、 \( \displaystyle \lim_{x\to a}f(x)=f(a) \) が成り立つことをいう。
また、関数 \( f(x) \) が \( x=a \) で連続でないとき、 \( x=a \) で不連続という。
区間における連続性
不等式
$$ a<x<b, \quad a≦ x<b, \quad a<x≦ b, \quad a≦ x≦ b $$
をみたす \( x \) 全体の集合を区間といい、それぞれ
$$ (a,b), \quad [a,b), \quad (a,b], \quad [a,b] $$
と表します。
特に、 \( (a,b) \) を開区間、 \( [a,b] \) を閉区間といいます。
また、不等式
$$ a<x, \quad a≦ x, \quad x<b, \quad x≦ b $$
をみたす \( x \) 全体の集合も区間といい、それぞれ
$$ (a,\infty), \quad [a,\infty), \quad (-\infty,b), \quad (-\infty,b] $$
と表します。
また、実数全体の集合を \( (-\infty,\infty) \) と表します。
(1) \( 2<x<5 \) の集合は \( (2,5) \)
(2) \( -3≦ x ≦ 4 \) の集合は \( [-3,4] \)
(3) \( x≦ 7 \) の集合は \( (-\infty,7] \)
これにより、区間 \( I \) における連続性というものを次で定義できます。
関数 \( f(x) \) がある区間 \( I \) に属するすべての \( x \) の値において連続であるとき、 \( f(x) \) は区間 \( I \) において連続であるという。
(1) \( 2x^2-5, \ x^3-6x+9 \) のような \( x \) の整式(多項式)で表される関数は区間 \( (-\infty,\infty) \) において連続である。
(2) 三角関数 \( \sin x, \ \cos x \) と指数関数 \( a^x \) は区間 \( (-\infty,\infty) \) において連続である。
また、対数関数 \( \log_ax \) は区間 \( (0,\infty) \) において連続である。
(3) 分数関数の定義域は、分母が0となる値を境目にいくつかの区間に分けられる。
そのそれぞれの区間において連続である。
たとえば、 \( \frac{2x-3}{x-2} \) は、 \( (-\infty,2), \ (2,\infty) \) において連続である。
(4) 無理関数 \( \sqrt{x} \) は区間 \( [0,\infty) \) において連続である。
実数 \( x \) に対して、 \( n≦ x<n+1 \) をみたす整数 \( n \) を \( [x] \) で表し、ガウス記号という。
$$ [2]=2, \ [2.4]=2, \ [-1.7]=-2 $$
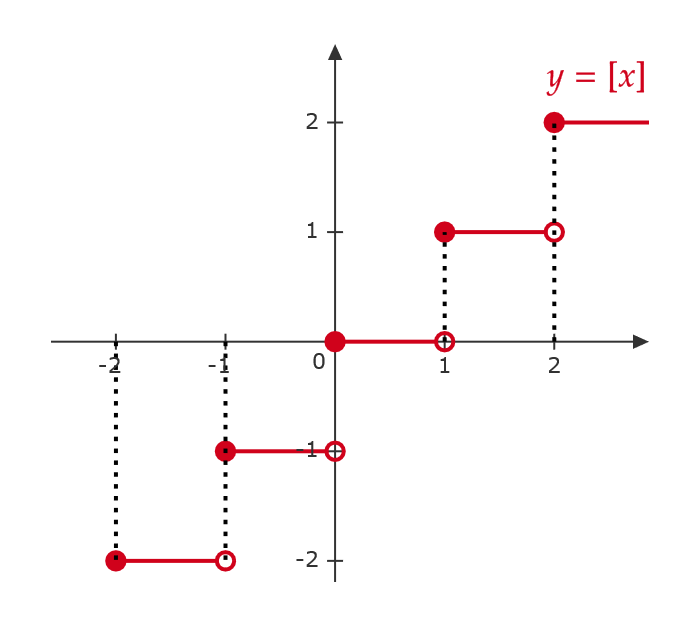
たとえば、 \( x=2 \) のとき、
$$ \lim_{x\to 2+0}[x]=2, \quad \lim_{x\to 2-0}[x]=1 $$
より、 \( \displaystyle \lim_{x\to 2}[x] \) は存在しない。
よって、 \( [x] \) は \( x=2 \) において不連続である。
連続関数の最大値・最小値
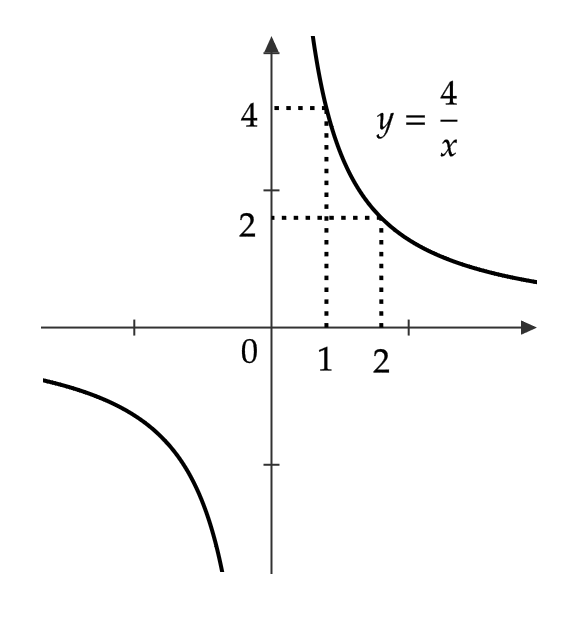
\( f(x)=\frac{4}{x} \) は \( (0,\infty) \) で連続であるが、
$$ \lim_{x\to+0}f(x)=\infty, \quad \lim_{x\to\infty}f(x)=0 $$
よって、 \( (0,\infty) \) 上で \( f(x) \) は最大値と最小値はもたない。
しかし、閉区間 \( [1,2] \) 上で考えると、最大値は \( f(1)=4 \)、最小値は \( f(2)=2 \) となります。
この例に限らず、一般的に次が成り立ちます。
閉区間上で連続な関数は、その区間上で最大値・最小値をもつ。
中間値の定理
閉区間 \( [a,b] \) 上の連続関数 \( f(x) \) のグラフは点 \( (a,f(a)) \) から点 \( (b,f(b)) \) の間で切れ目なく続いています。
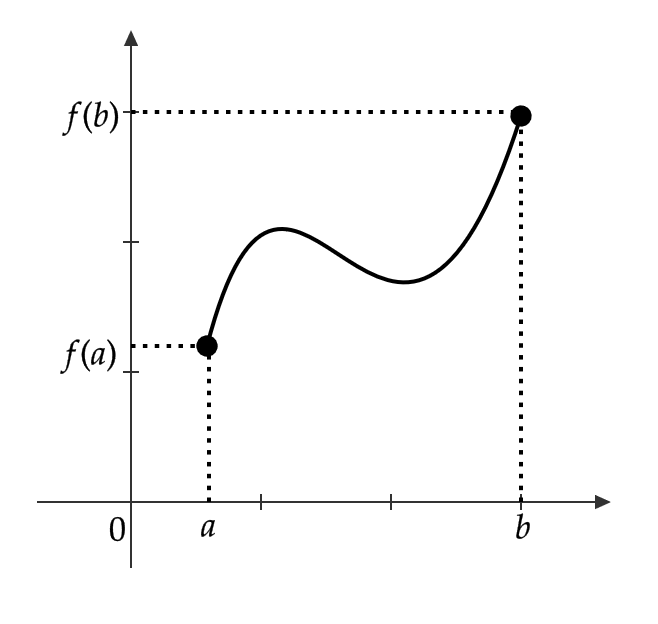
このことから、次が成り立ちます。
関数 \( f(x) \) が閉区間 \( [a,b] \) において連続で \( f(a)\not=f(b) \) ならば、 \( f(a) \) と \( f(b) \) の間の任意の値 \( m \) に対して、
$$ f(c)=m \quad (a<c<b) $$
となる \( c \) が少なくとも1つ存在する。
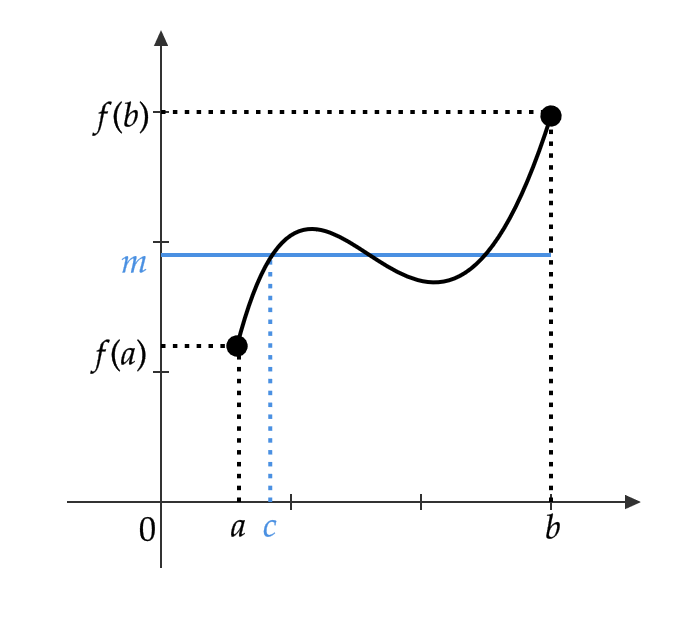
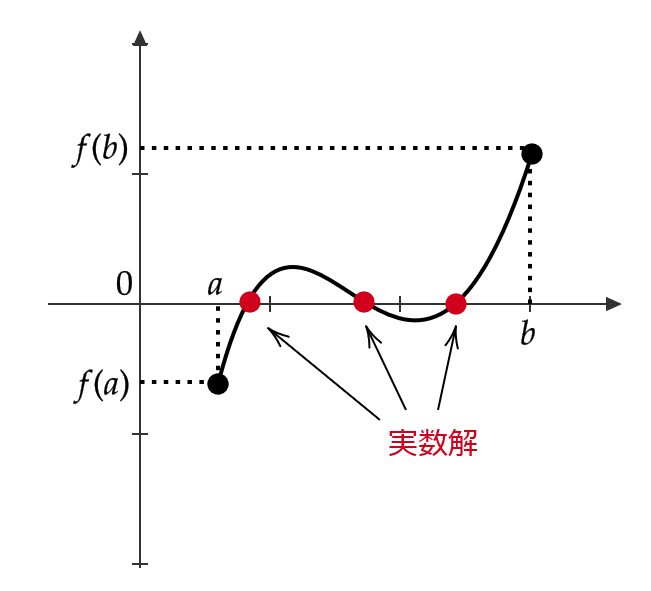
中間値の定理から次が成り立ちます。
関数 \( f(x) \) が閉区間 \( [a,b] \) において連続であり、 \( f(a) \) と \( f(b) \) が異符号であるとき、方程式 \( f(x)=0 \) は、 \( a \) と \( b \) の間に少なくとも1つの実数解をもつ。
方程式 \( 3^x-6x+2=0 \) は \( 2<x<3 \) の範囲で少なくとも1つの実数解をもつことを示す。
\( f(x)=3^x-6x+2 \) とおくと、 \( f(x) \) は閉区間 \( [2,3] \) で連続である。
また、
$$ \begin{align} f(2)&=3^2-6\times2+2=-1<0 \\ f(3)&=3^3-6\times3+2=11>0 \end{align} $$
よって、中間値の定理より、この方程式は \( 2<x<3 \) の範囲で少なくとも1つの実数解をもつ。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

