こんにちは、ひかりです。
今回は高校数学から関数の極限について解説していきます。
数列の極限について知りたい方は前回の記事をご覧ください。
この記事では以下のことを紹介します。
- 関数の極限について
- 指数関数・対数関数の極限について
- 三角関数の極限について
関数の極限
関数の極限
数列の極限と同じようにして、関数の極限を次のようにして定めます。
関数 \( f(x) \) において、 \( x \) が \( a \) とは異なる値をとりながら限りなく \( a \) に近づくとき、 \( f(x) \) が一定の値 \( \alpha \) に限りなく近づくとする。このとき、 \( x\to a \) のとき \( f(x) \) は \( \alpha \) に収束するといい、
$$ \lim_{x\to a}f(x)=\alpha \quad \text{または} \quad f(x)\to \alpha \ (x\to a) $$
と表し、 \( \alpha \) を \( x\to a \) のときの \( f(x) \) の極限値という。
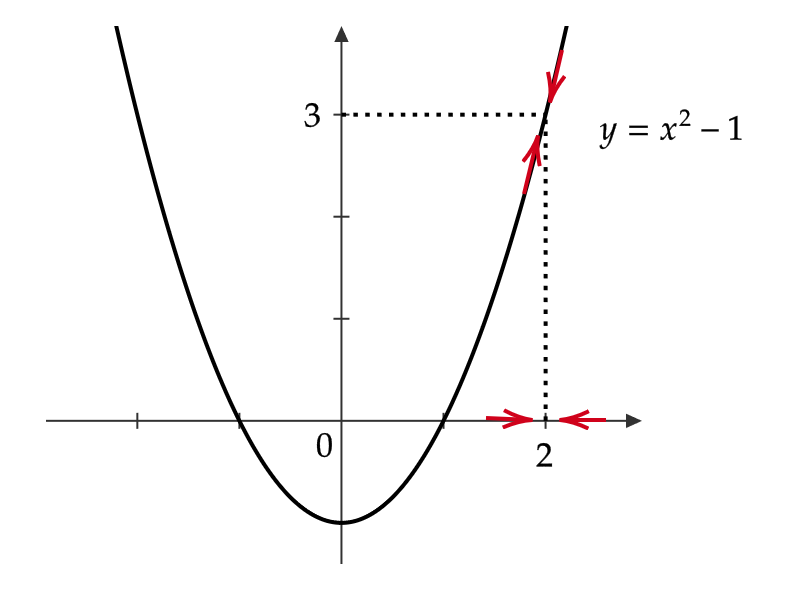
\( f(x)=x^2-1 \) を考える。
\( x\to 2 \) のとき、 \( f(x)\to f(2) \) である。よって、
$$ \lim_{x\to 2}f(x)=f(2)=3 $$
関数 \( y=f(x) \) の \( x=a \) での値 \( f(a) \) が定義されていなくても、極限値 \( \displaystyle \lim_{x\to a}f(x) \) が存在する場合もあります。
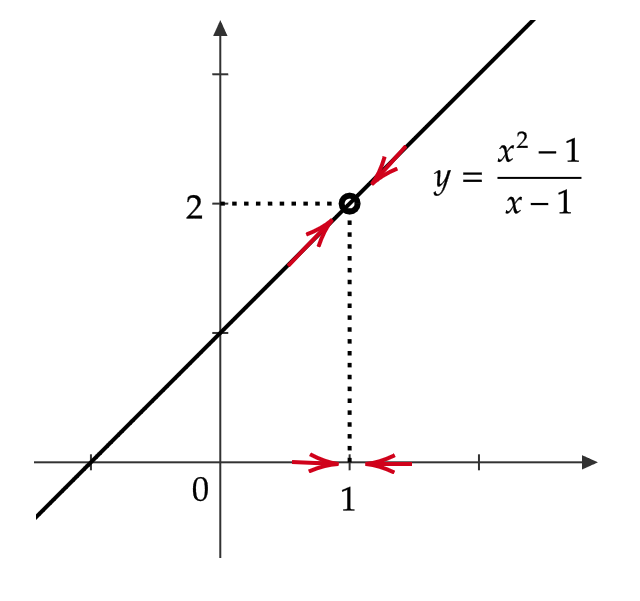
\( f(x)=\frac{x^2-1}{x-1} \) は \( x\not=1 \) のとき定義されない。
しかし、 \( x\not=1 \) のとき
$$ f(x)=\frac{x^2-1}{x-1}=\frac{(x-1)(x+1)}{x-1}=x+1 $$
となるので、 \( x \) が限りなく \( 1 \) に近づくとき、 \( f(x) \) は限りなく \( 2 \) に近づく。よって、
$$ \lim_{x\to 1}\frac{x^2-1}{x-1}=2 $$
関数の極限値の性質について、次が成り立ちます。
関数 \( f(x),g(x) \) が収束して、 \( \displaystyle \lim_{x\to a}f(x)=\alpha, \ \lim_{x\to a}g(x)=\beta \) のとき、次が成り立つ。
(1) \( \displaystyle \lim_{x\to a}kf(x)=k\alpha \quad (k\text{は定数}) \)
(2) \( \displaystyle \lim_{x\to a}(f(x)+g(x))=\alpha+\beta \)
\( \displaystyle \lim_{x\to a}(f(x)-g(x))=\alpha-\beta \)
(3) \( \displaystyle \lim_{x\to a}f(x)g(x)=\alpha\beta \)
(4) \( \displaystyle \lim_{x\to a}\frac{f(x)}{g(x)}=\frac{\alpha}{\beta} \quad (\beta\not=0) \)
(1) \( \displaystyle \lim_{x\to 2}(x^2-x+2)(3x-1) \) を求める。
$$ \lim_{x\to 2}(x^2-x+2)(3x-1)=4\times 5=20 $$
(2) \( \displaystyle \lim_{x\to 1}\frac{x^2-x}{x^2+x-2} \) を求める。
$$ \lim_{x\to 1}\frac{x^2-x}{x^2+x-2}=\lim_{x\to 1}\frac{x(x-1)}{(x-1)(x+2)}=\lim_{x\to 1}\frac{x}{x+2}=\frac{1}{3} $$
(3) \( \displaystyle \lim_{x\to 0}\frac{1-\sqrt{1-x}}{x} \) を求める。
$$ \begin{align} \lim_{x\to 0}\frac{1-\sqrt{1-x}}{x}&=\lim_{x\to 0}\frac{(1-\sqrt{1-x})(1+\sqrt{1-x})}{x(1+\sqrt{1-x})} \\ &=\lim_{x\to 0}\frac{1-(1-x)}{x(1+\sqrt{1-x})} \\ &=\lim_{x\to 0}\frac{x}{x(1+\sqrt{1-x})} \\ &=\lim_{x\to 0}\frac{1}{1+\sqrt{1-x}}=\frac{1}{2} \end{align} $$
また、関数の発散についても、数列と同様に定義されます。
(1) 関数 \( f(x) \) において、 \( x \) が \( a \) とは異なる値をとりながら限りなく \( a \) に近づくとき、 \( f(x) \) が限りなく大きくなるとする。このとき、 \( x\to a \) のとき \( f(x) \) は正の無限大に発散するといい、
$$ \lim_{x\to a}f(x)=\infty \quad \text{または} \quad f(x)\to \infty \ (x\to a) $$
と表す。
(2) 関数 \( f(x) \) において、 \( x \) が \( a \) とは異なる値をとりながら限りなく \( a \) に近づくとき、 \( f(x) \) の値が負でその絶対値 \( |f(x)| \) が限りなく大きくなるとする。このとき、 \( x\to a \) のとき \( f(x) \) は負の無限大に発散するといい、
$$ \lim_{x\to a}f(x)=-\infty \quad \text{または} \quad f(x)\to -\infty \ (x\to a) $$
と表す。
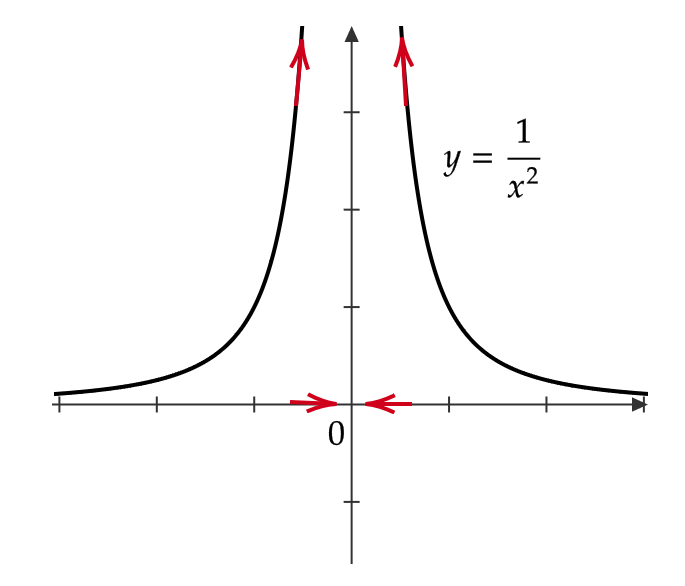
(1) \( \displaystyle \lim_{x\to 0}\frac{1}{x^2}=\infty \)
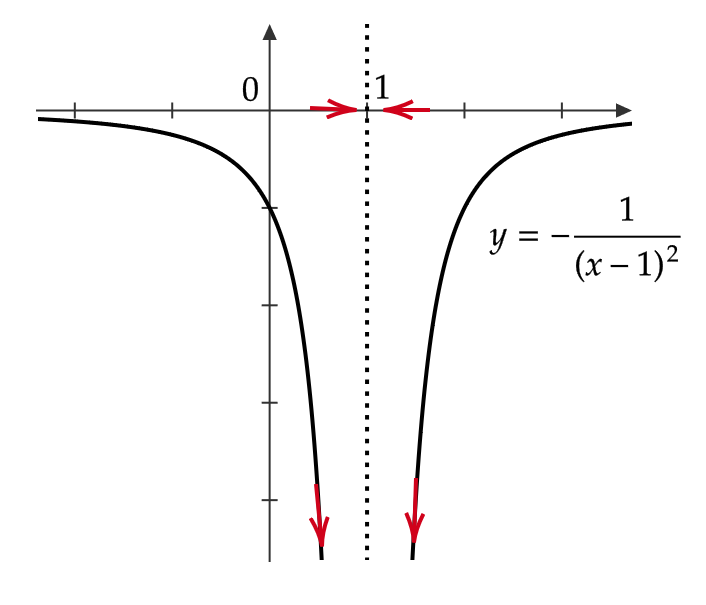
(2) \( \displaystyle \lim_{x\to 1}\left\{ -\frac{1}{(x-1)^2} \right\}=-\infty \)
右側からの極限・左側からの極限
\( f(x)=\frac{x(x-1)}{|x|} \) を考える。
\( x>0 \) のとき
$$ f(x)=\frac{x(x-1)}{x}=x-1 $$
\( x<0 \) のとき
$$ f(x)=\frac{x(x-1)}{-x}=-x+1 $$
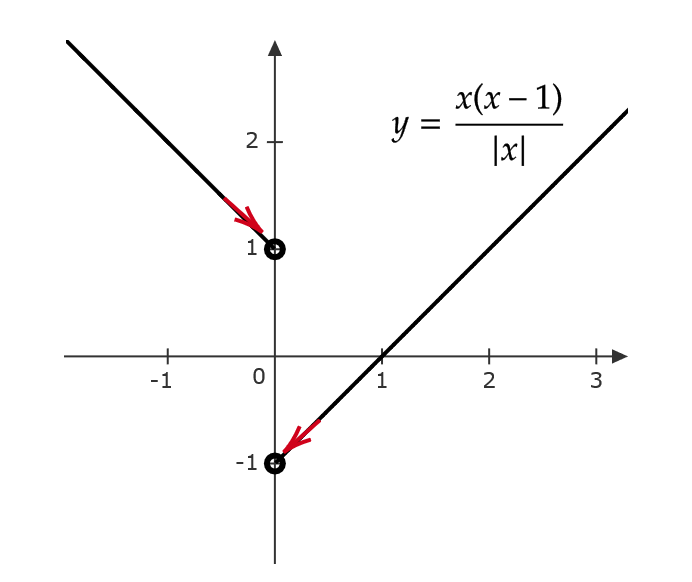
よって、 \( x \) が右側から限りなく \( 0 \) に近づくとき、 \( f(x) \) は \( -1 \) に近づく。
また、 \( x \) が左側から限りなく \( 0 \) に近づくとき、 \( f(x) \) は \( 1 \) に近づく。
この例のように右側から近づけた場合と左側から近づけた場合で極限値が異なる場合があります。
よって、右側からの極限と左側からの極限をそれぞれ定める必要があります。
(1) 関数 \( f(x) \) において、 \( x \) が \( a \) より大きい値をとって限りなく \( a \) に近づくとき、 \( f(x) \) が一定の値 \( \alpha \) に限りなく近づくとする。このとき、 \( \alpha \) を \( x \) を右側から \( a \) に近づくときの \( f(x) \) の極限値といい、 \( \displaystyle \lim_{x\to a+0}f(x)=\alpha \) とかく。
(2) 関数 \( f(x) \) において、 \( x \) が \( a \) より小さい値をとって限りなく \( a \) に近づくとき、 \( f(x) \) が一定の値 \( \alpha \) に限りなく近づくとする。このとき、 \( \alpha \) を \( x \) を左側から \( a \) に近づくときの \( f(x) \) の極限値といい、 \( \displaystyle \lim_{x\to a-0}f(x)=\alpha \) とかく。
とくに、 \( a=0 \) のときは \( x\to 0+0 \) を単に \( x\to +0 \)、 \( x\to 0-0 \) を単に \( x\to -0 \) と書きます。
(1) 例5を \( \lim \) を用いて表すと、
$$ \lim_{x\to +0}\frac{x(x-1)}{|x|}=\lim_{x\to +0}(x-1)=-1 $$
$$ \lim_{x\to -0}\frac{x(x-1)}{|x|}=\lim_{x\to -0}(-x+1)=1 $$
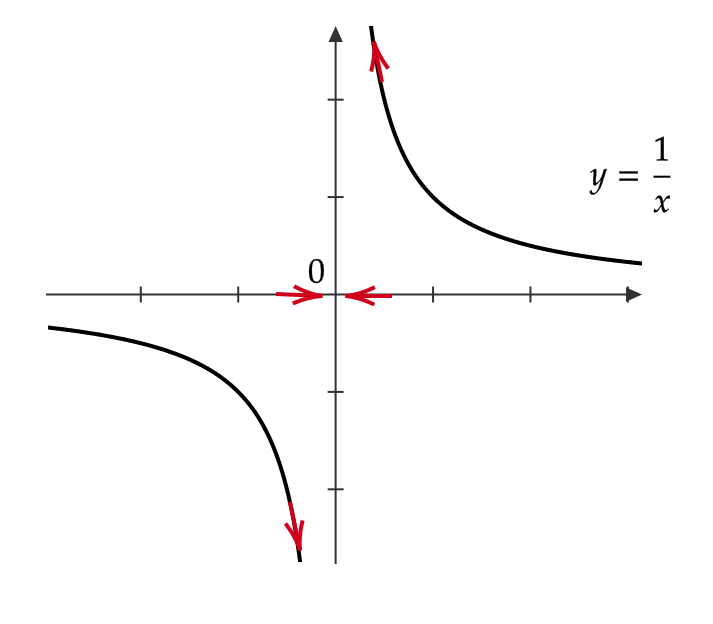
(2) \( \displaystyle \lim_{x\to +0}\frac{1}{x}=\infty, \ \lim_{x\to -0}\frac{1}{x}=-\infty \)
\( x\to\infty, \ x\to-\infty \) のときの極限
(1) \( x\to\infty \) のときに \( f(x) \) の値が限りなく \( \alpha \) に近づくとき、 \( \displaystyle \lim_{x\to\infty}f(x)=\alpha \) と表す。
(2) \( x\to-\infty \) のときに \( f(x) \) の値が限りなく \( \alpha \) に近づくとき、 \( \displaystyle \lim_{x\to-\infty}f(x)=\alpha \) と表す。
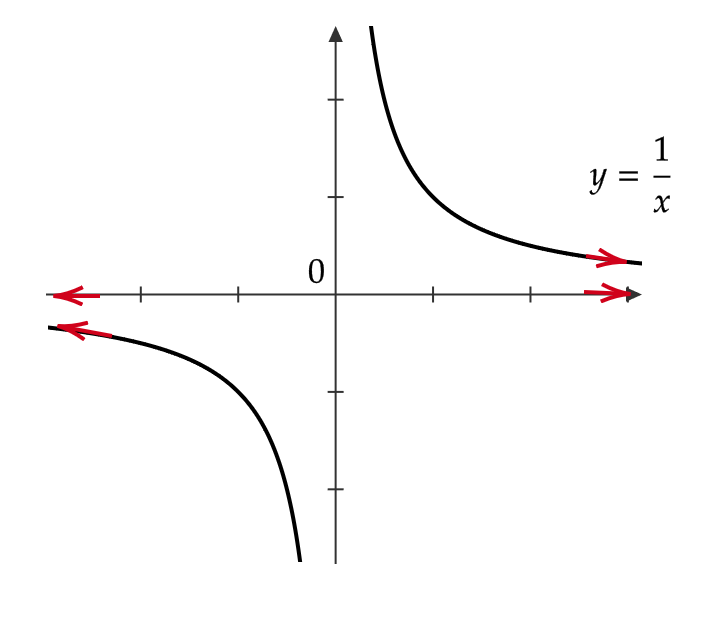
(1) \( \displaystyle \lim_{x\to \infty}\frac{1}{x}=0, \ \lim_{x\to -\infty}\frac{1}{x}=0 \)
(2) \( \displaystyle \lim_{x\to\infty}\frac{x^2+x+5}{6x^2+3x+4} \) を求める。
$$ \begin{align} \lim_{x\to\infty}\frac{x^2+x+5}{6x^2+3x+4}=\lim_{x\to\infty}\frac{1+\frac{1}{x}+\frac{5}{x^2}}{6+\frac{3}{x}+\frac{4}{x^2}}=\frac{1}{6} \end{align} $$
(3) \( \displaystyle \lim_{x\to\infty}(\sqrt{x^2-x+1}-x) \) を求める。
$$ \begin{align} &\lim_{x\to\infty}(\sqrt{x^2-x+1}-x) \\ =&\lim_{x\to\infty}\frac{(\sqrt{x^2-x+1}-x)(\sqrt{x^2-x+1}+x)}{\sqrt{x^2-x+1}+x} \\ =&\lim_{x\to\infty}\frac{(x^2-x+1)-x^2}{\sqrt{x^2-x+1}+x}=\lim_{x\to\infty}\frac{-x+1}{\sqrt{x^2-x+1}+x} \\ &=\lim_{x\to\infty}\frac{-1+\frac{1}{x}}{\sqrt{1-\frac{1}{x}+\frac{1}{x^2}}+1}=-\frac{1}{2} \end{align} $$
(4) \( \displaystyle \lim_{x\to-\infty}(x^3+2x^2-3x+1) \) を求める。
$$ \begin{align} \lim_{x\to-\infty}(x^3+2x^2-3x+1)&=\lim_{x\to-\infty}x^3\left(1+\frac{2}{x}-\frac{3}{x^2}+\frac{1}{x^3}\right) \\ &=-\infty \end{align} $$
指数関数・対数関数の極限
ここでは、指数関数・対数関数の極限についてまとめていきます。
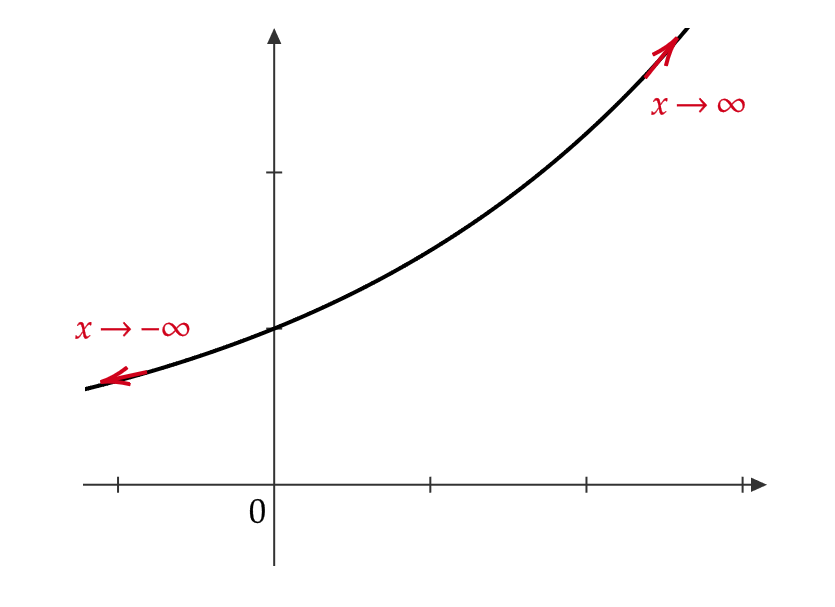
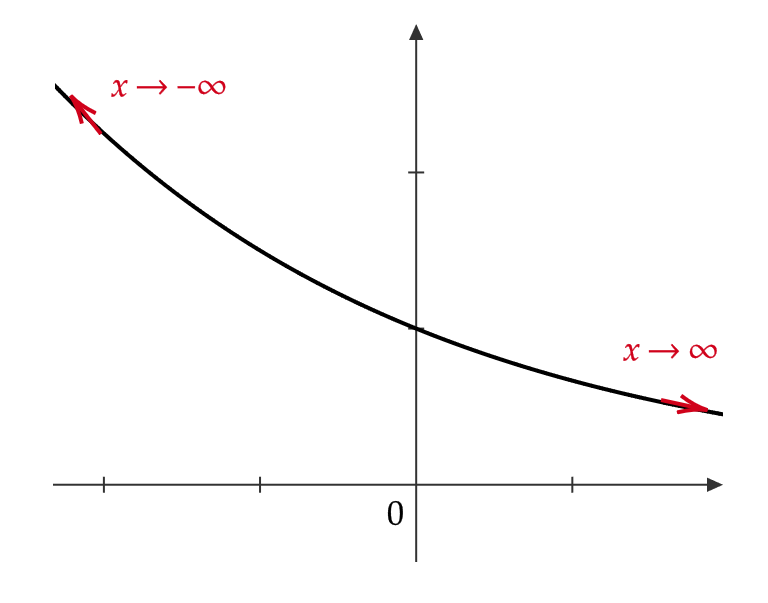
(1) \( a>1 \) のとき
$$ \lim_{x\to\infty}a^x=\infty, \quad \lim_{x\to-\infty}a^x=0 $$
(2) \( 0<a<1 \) のとき
$$ \lim_{x\to\infty}a^x=0, \quad \lim_{x\to-\infty}a^x=\infty $$
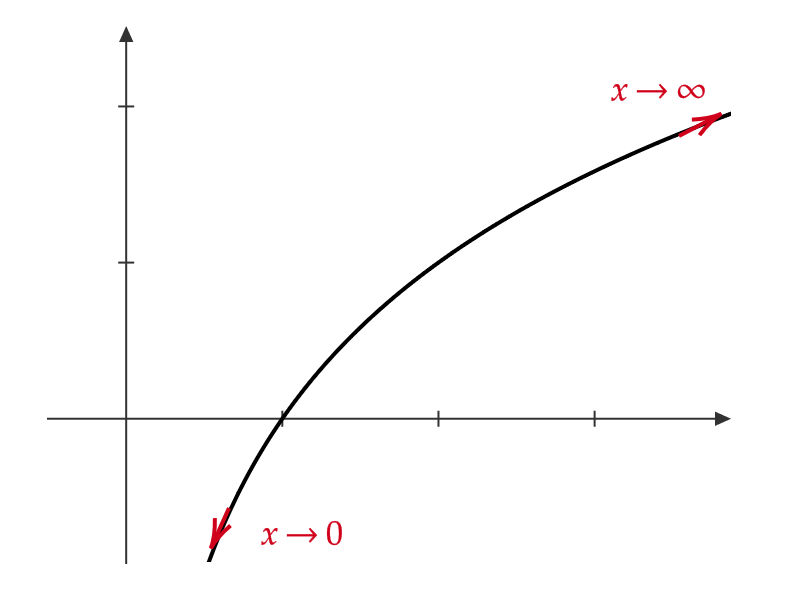
(3) \( a>1 \) のとき
$$ \lim_{x\to\infty}\log_ax=\infty, \quad \lim_{x\to+0}\log_ax=-\infty $$
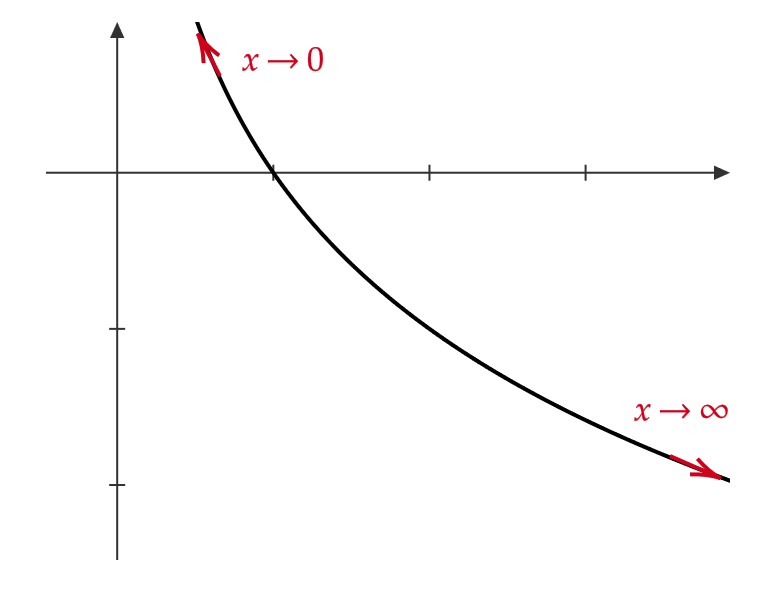
(4) \( 0<a<1 \) のとき
$$ \lim_{x\to\infty}\log_ax=-\infty, \quad \lim_{x\to+0}\log_ax=\infty $$
(1) \( \displaystyle \lim_{x\to+0}\log_{\frac{1}{2}}x=\infty \)
(2) \( \displaystyle \lim_{x\to\infty}(5^x-2^x) \) を求める。
$$ \lim_{x\to\infty}(5^x-2^x)=\lim_{x\to\infty}5^x\left\{ 1-\left(\frac{2}{5}\right)^x\right\}=\infty $$
三角関数の極限
三角関数の極限
まず、 \( y=\sin x, \ y=\cos x \) は \( -1 \) と \( 1 \) との間をくり返しているので、 \( \displaystyle \lim_{x\to \infty}\sin x \) と \( \displaystyle \lim_{x\to \infty}\cos x \) は存在しません。
また、 \( y=\tan x \) については、 \( \displaystyle \lim_{x\to \frac{\pi}{2}-0}\tan x=\infty, \ \lim_{x\to \frac{\pi}{2}+0}\tan x=-\infty \) であるので、 \( \displaystyle \lim_{x\to \frac{\pi}{2}}\tan x \) は存在しません。
しかし、これで終わりではつまらないため、もう少し見ていきましょう。
関数の極限値の大小関係
その準備として、関数の極限値の大小関係について紹介していきます。
数列の極限値の大小関係と同様に次のことが成り立ちます。
(1) 関数 \( f(x), \ g(x) \) が \( a \) の近くで \( f(x)≦ g(x) \) が成り立ち、
$$ \lim_{x\to a}f(x)=\alpha, \quad \lim_{x\to a}g(x)=\beta $$
ならば、 \( \alpha≦\beta \)
(2) (はさみうちの原理)
関数 \( f(x), \ g(x), \ h(x) \) が \( a \) の近くで \( f(x)≦ g(x)≦ h(x) \) が成り立ち、
$$ \lim_{x\to a}f(x)=\lim_{x\to a}h(x)=\alpha $$
ならば、 \( \displaystyle \lim_{x\to a}g(x)=\alpha \)
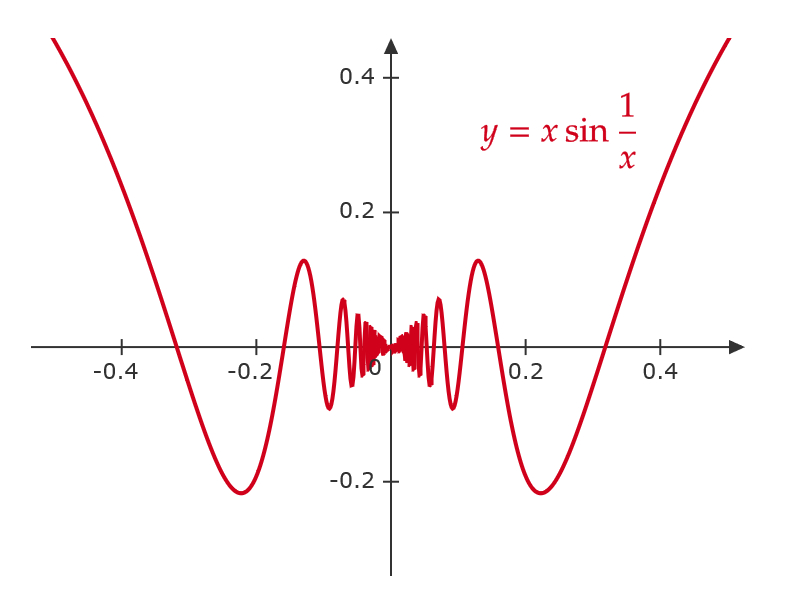
\( \displaystyle \lim_{x\to0}x\sin \frac{1}{x} \) を計算する。
\( \displaystyle 0≦ \left|\sin \frac{1}{x}\right|≦ 1 \) より、
$$ 0≦ \left|x\sin \frac{1}{x}\right|≦ |x| $$
ここで、 \( \displaystyle \lim_{x\to 0}|x|=0 \) であるので、はさみうちの原理より、
$$ \lim_{x\to 0}\left|x\sin \frac{1}{x}\right|=0 $$
よって、 \( \displaystyle \lim_{x\to 0}x\sin \frac{1}{x}=0 \)
\( \frac{\sin\theta}{\theta} \) の極限
実は、三角関数の極限において重要となる極限は \( \displaystyle \lim_{\theta\to 0}\frac{\sin\theta}{\theta} \) となります。
なぜなら、さまざまな三角関数は \( \frac{\sin\theta}{\theta} \) を含む形に変形することができるからです。
ただしこの極限は、はさみうちの原理によって求められるのですが導出が少し難しいため、公式として結果を覚えるというかたちで問題ありません。
気になる方のみ導出の仕方をご覧ください。
\( \displaystyle \lim_{\theta\to 0}\frac{\sin\theta}{\theta} \) の求め方 (気になる方のみご覧ください)
\( 0<\theta<\frac{\pi}{2} \) として、半径1の円 \( O \) の円周上に \( \angle AOB=\theta \) となる2点 \( A,B \) をとります。
点 \( A \) における円の接線と \( OB \) の交点を \( T \) とすると、面積について
$$ \triangle OAB=\frac{1}{2} \sin \theta $$
$$ \triangle OAT=\frac{1}{2} \tan \theta $$
$$ \text{扇形} \ OAB=\frac{1}{2}r^2\theta=\frac{1}{2}\theta $$
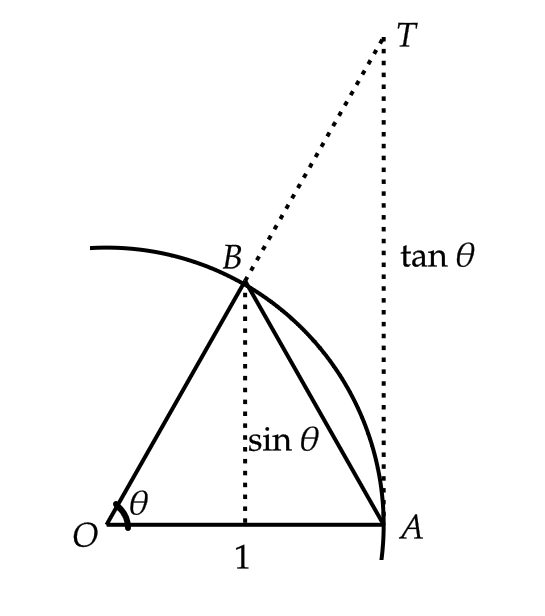
図より面積を比較すると、\( \triangle OAB<\text{扇形} \ OAB<\triangle OAT \) となるので、
$$ \sin\theta<\theta<\tan\theta $$
各辺を \( \sin\theta \) で割ると、 \( \sin\theta>0 \) より、
$$ 1<\frac{\theta}{\sin\theta}<\frac{\tan\theta}{\sin\theta}=\frac{1}{\cos\theta} $$
逆数をとると、
$$ 1>\frac{\sin\theta}{\theta}>\cos\theta $$
\( \displaystyle \lim_{\theta\to +0}\cos\theta=1 \) ( \( 0<\theta<\frac{\pi}{2} \) より \( \theta\to+0 \) )であるので、はさみうちの原理より、
$$ \lim_{\theta\to 0}\frac{\sin\theta}{\theta}=1 $$
\( \theta<0 \) のときは、 \( \theta=-t \) とおくと \( t>0 \) なので、
$$ \lim_{\theta\to-0}\frac{\sin\theta}{\theta}=\lim_{t\to+0}\frac{\sin (-t)}{-t}=\lim_{t\to+0}\frac{\sin t}{t}=1 $$
$$ \lim_{\theta\to 0}\frac{\sin\theta}{\theta}=1 $$
(1) \( \displaystyle \lim_{x\to 0}\frac{\sin 2x}{x} \) を求める。
$$ \begin{align} \lim_{x\to 0}\frac{\sin 2x}{x}&=\lim_{x\to0}2\left( \frac{\sin 2x}{2x} \right) \overset{\theta=2x\text{とおく}}{=} 2\cdot \lim_{\theta\to0}\frac{\sin \theta}{\theta} \\ &=2\times 1=2 \end{align} $$
(2) \( \displaystyle \lim_{x\to 0}\frac{\sin 7x+\sin 5x}{\sin 2x} \) を求める。
$$ \begin{align} \lim_{x\to 0}\frac{\sin 7x+\sin 5x}{\sin 2x}&=\lim_{x\to0}\frac{\frac{\sin 7x}{x}+\frac{\sin 5x}{x}}{\frac{\sin 2x}{x}} \\ &=\lim_{x\to0}\frac{7\cdot \frac{\sin 7x}{7x}+5\cdot\frac{\sin 5x}{5x}}{2\cdot\frac{\sin 2x}{2x}} \\ &=\frac{7\times 1+5\times 1}{2\times 1}=6 \end{align} $$
(3) \( \displaystyle \lim_{x\to 0}\frac{1-\cos x}{x^2} \) を求める。
$$ \begin{align} \lim_{x\to 0}\frac{1-\cos x}{x^2}&=\lim_{x\to0}\frac{(1-\cos x)(1+\cos x)}{x^2(1+\cos x)} \\ &=\lim_{x\to0}\frac{1-\cos^2 x}{x^2(1+\cos x)} \\ &\overset{\sin^2x+\cos^2x=1}{=} \lim_{x\to0}\frac{\sin^2x}{x^2(1+\cos x)} \\ &=\lim_{x\to0}\frac{1}{1+\cos x}\left( \frac{\sin x}{x} \right)^2 \\ &=\frac{1}{2} \quad (\lim_{x\to0}\cos x=1 \ \text{に注意}) \end{align} $$
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

