こんにちは、ひかりです。
今回は高校数学から指数関数・対数関数について解説していきます。
この記事では以下のことを紹介します。
- 指数法則と指数関数について
- 対数の性質と対数関数について
指数関数
指数法則
\( a\not=0 \) とします。このとき、 \( a \) を \( n \) 個かけ合わせたものを \( a \) の \( n \) 乗といい、 \( a^n \) と表します。
また、 \( a \) をいくつか掛けたものを \( a \) の累乗といいます。
このとき、正の整数 \( m,n \) に対して、次の指数法則が成り立ちます。
(i) \( a^ma^n=a^{m+n} \)
(ii) \( (a^m)^n=a^{mn} \)
(iii) \( (ab)^n=a^nb^n \)
\( a^n \) の定義を \( n \) が \( 0 \) や負の整数に対しても拡張することを考えます。
そこで、次の図のように \( a \) を一つずつ掛けたり、割ったりしてみます。
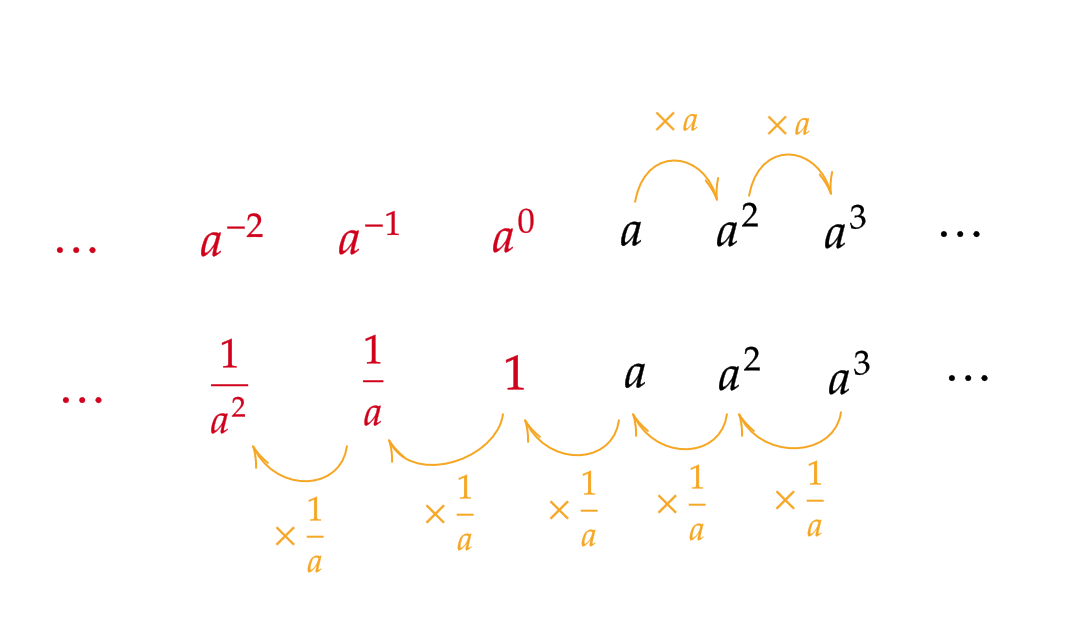
これにより、指数が \( 0 \) または負の整数のときの累乗を次で定めることができます。
\( a\not=0 \) で \( n \) が正の整数のとき、
$$ a^0=1, \quad a^{-n}=\frac{1}{a^n} $$
(1) \( 3^0=1 \)
(2) \( 2^{-3}=\frac{1}{2^3}=\frac{1}{8} \)
これにより、 \( m,n \) :整数に対して、定理1の指数法則が成り立ちます。
(1) 指数法則(i)について
$$ a^3a^{-2}=a^3\times \frac{1}{a^2}=a=a^{3+(-2)} $$
(2) 指数法則(ii)について
$$ (a^3)^{-2}=\frac{1}{(a^3)^2}=\frac{1}{a^6}=a^{-6}=a^{3\times(-2)} $$
(3) 指数法則(iii)について
$$ (ab)^{-2}=\frac{1}{(ab)^2}=\frac{1}{a^2b^2}=\frac{1}{a^2}\times \frac{1}{b^2}=a^{-2}b^{-2} $$
次に、指数を有理数に拡張していきます。
ここで、 \( n \) 乗して \( a \) になる数、すなわち \( x^n=a \) となる \( x \) を \( a \) の \( n \) 乗根といいます。
また、1乗根、2乗根、… を総称して累乗根といいます。
(1) \( (-2)^3=-8 \) より、 \( -2 \) は \( -8 \) の \( 3 \) 乗根である。これを \( \sqrt[3]{-8}=-2 \) と表す。
(2) \( (-2)^4=16, \ 2^4=16 \) より、 \( -2, \ 2 \) は \( 16 \) の \( 4 \) 乗根である。これを \( \sqrt[4]{16}=2, \ -\sqrt[4]{16}=-2 \) と表す。
累乗根の性質として、以下が成り立ちます。
\( a>0, \ b>0 \) で \( m,n,p \):正の整数のとき、次が成り立つ。
(i) \( \sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab} \)
(ii) \( \frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}} \)
(iii) \( (\sqrt[n]{a})^m=\sqrt[n]{a^m} \)
(iv) \( \sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a} \)
(v) \( \sqrt[np]{a^{mp}}=\sqrt[n]{a^m} \)
これにより、有理数の指数を次のように定めます。
\( a>0 \) 、 \( m \) :整数、 \( n \) :正の整数に対して、有理数の指数の累乗を次で定める。
$$ a^{\frac{m}{n}}=\sqrt[n]{a^m} $$
(1) \( 8^{\frac{2}{3}} \) を計算する。
$$ 8^{\frac{2}{3}}=\sqrt[3]{8^2}=\sqrt[3]{64}=\sqrt[3]{4^3}=4 $$
(2) \( 8^{-\frac{2}{3}} \) を計算する。
$$ 8^{-\frac{2}{3}}=\sqrt[3]{8^{-2}}=\sqrt[3]{\frac{1}{64}}=\frac{1}{\sqrt[3]{64}}=\frac{1}{\sqrt[3]{4^3}}=\frac{1}{4} $$
この定義により、指数が有理数に対しても定理1の指数法則が成り立ちます。
(1) 指数法則(i)について
$$ a^{\frac{2}{3}}a^{\frac{1}{3}}=\sqrt[3]{a^2}\times\sqrt[3]{a}=\sqrt[3]{a^2\times a}=\sqrt[3]{a^{2+1}}=a^{\frac{2+1}{3}}=a^{\frac{2}{3}+\frac{1}{3}} $$
(2) 指数法則(ii)について
$$ (a^{\frac{2}{3}})^{\frac{1}{3}}=(\sqrt[3]{a^2})^{\frac{1}{3}}=\sqrt[3]{\sqrt[3]{a^2}}=\sqrt[3\times 3]{a^2}=a^{\frac{2}{3\times3}}=a^{\frac{2}{3}\times \frac{1}{3}} $$
(3) 指数法則(iii)について
$$ (ab)^{\frac{2}{3}}=\sqrt[3]{(ab)^2}=\sqrt[3]{a^2b^2}=\sqrt[3]{a^2}\times\sqrt[3]{b^2}=a^{\frac{2}{3}}b^{\frac{2}{3}} $$
指数 \( p \) が無理数のときも次の例のように累乗 \( a^p \) が定義できます。
\( \sqrt{2}=1.41421\cdots \) に対して、列
$$ 3^1, \ 3^{1.4}, \ 3^{1.41}, \ 3^{1.414}, \ 3^{1.4142}, \ 3^{1.41421}, \cdots $$
を考えると、ある値に近づいていく。
その値を \( 3^{\sqrt{2}} \) と定める。
指数関数とそのグラフ
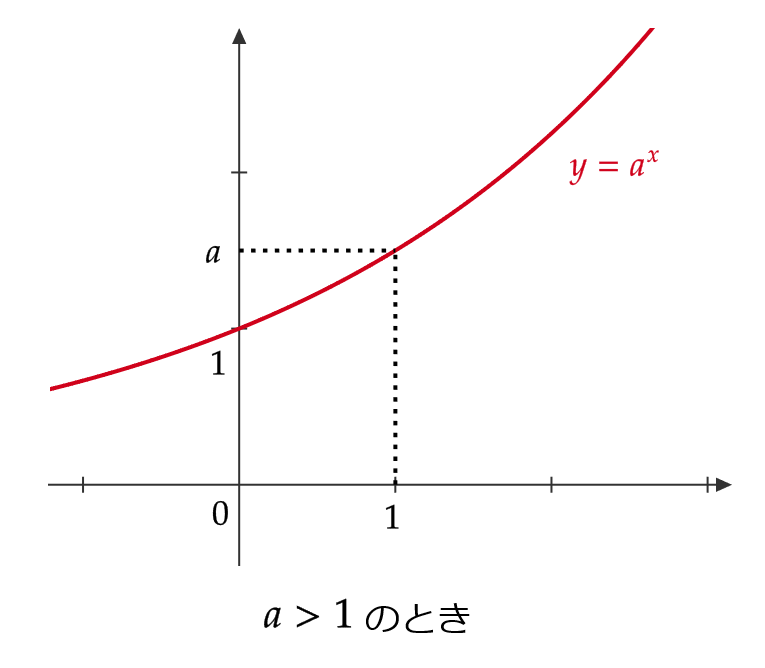
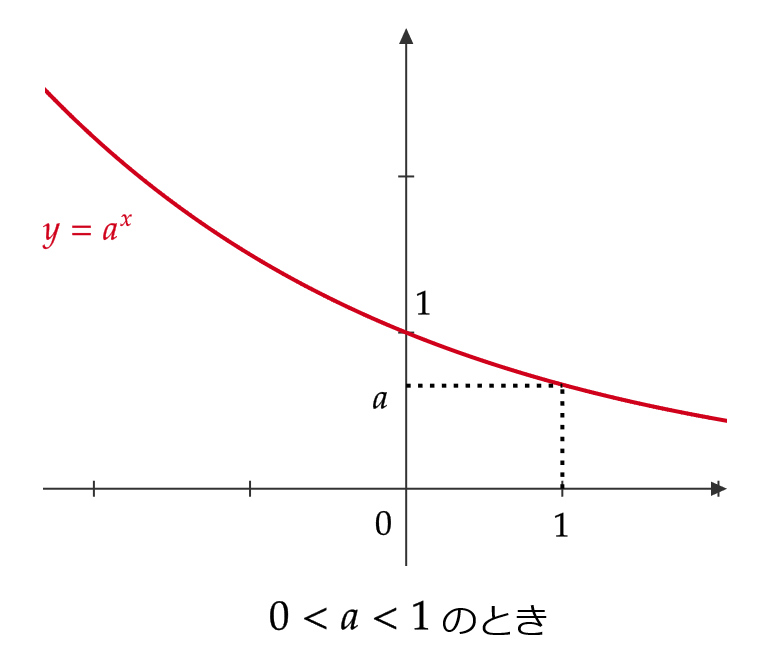
\( a>0 \) に対して、 \( y=a^x \) は次のようなグラフとなります。
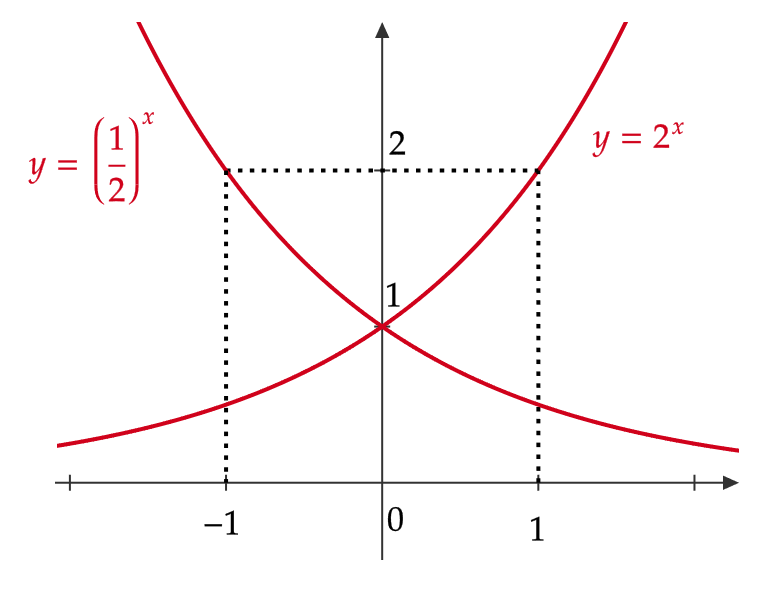
\( y=2^x \) と \( y=\left( \frac{1}{2} \right)^x \) のグラフを考える。
これらは \( y \) 軸に関して対称であることが図よりわかる。
対数関数
対数とその性質
\( a>0, \ a\not=1 \) とすると、指数関数 \( y=a^x \) のグラフより、任意の正の実数 \( M \) に対して、 \( a^p=M \) となる実数 \( p \) がただ一つ定まります。
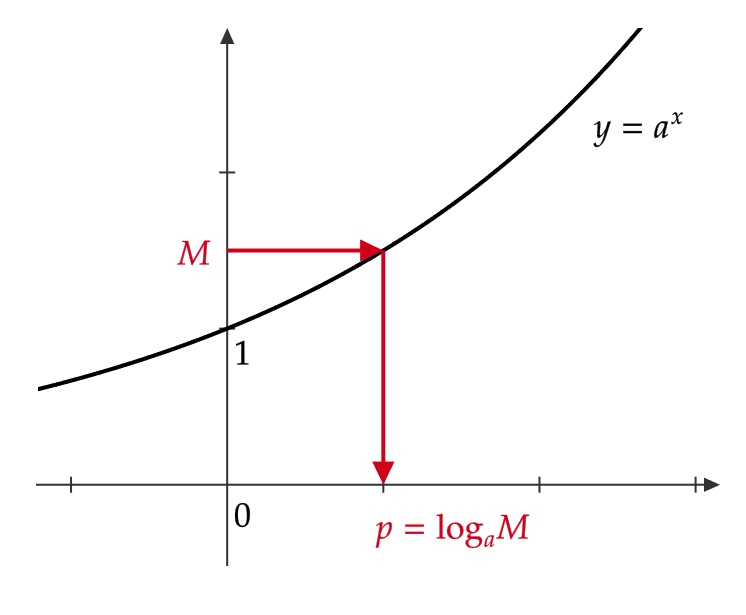
この \( p \) を \( \log_aM \) と表して、 \( a \) を底とする \( M \) の対数といいます。
また、 \( M \) を \( \log_aM \) の真数といいます。
つまり、指数と対数の関係は次のようになります。
\( a>0, \ a\not=1, \ M>0 \) のとき、
$$ \log_aM=p \Longleftrightarrow a^p=M $$
(1) \( 2^3=8 \) より、 \( \log_28=3 \)
(2) \( \log_3x=-2 \) をみたす \( x \) は \( x=3^{-2}=\frac{1}{9} \)
(3) \( \log_84 \) を求める。 \( \log_84=x \) とおくと、 \( 8^x=4 \) となる。
\( 8^x=(2^3)^x=2^{3x}, \ 4=2^2 \) より、 \( 2^{3x}=2^2 \)
よって、 \( 3x=2 \) より、 \( \log_84=x=\frac{2}{3} \)
対数に関して、次のような性質が成り立ちます。
\( a>0, \ a\not=1, \ M>0, \ N>0 \) に対して、
$$ \log_a1=0, \ \log_aa=1, \ \log_aa^p=p $$
また、指数法則より、次が成り立つ。
(i) \( \log_aMN=\log_aM+\log_aN \)
(ii) \( \log_a\frac{M}{N}=\log_aM-\log_aN \)
(iii) \( \log_aM^r=r\log_aM \)
(1) \( \log_2\frac{4}{3}+\log_224 \) を計算する。
$$ \begin{align} \log_2\frac{4}{3}+\log_224&=\log_2\left( \frac{4}{3}\times 24 \right) \\ &=\log_232=\log_22^5=5 \end{align} $$
(2) \( 6\log_3\sqrt{6}-\log_28 \) を計算する。
$$ \begin{align} 6\log_3\sqrt{6}-\log_28 &=\log_3(6^{\frac{1}{2}})^6-\log_32^3 \\ &=\log_36^3-\log_32^3 \\ &=\log_3\frac{6^3}{2^3}=\log_33^3=3 \end{align} $$
対数の底を変えたいときに有用な底の変換公式について紹介する。
\( a,b,c>0 \) で \( a\not=1, \ c\not=1 \) のとき、次が成り立つ。
$$ \log_ab=\frac{\log_cb}{\log_ca} $$
$$ \log_{27}9=\frac{\log_39}{\log_327}=\frac{\log_33^2}{\log_33^3}=\frac{2\log_33}{3\log_33}=\frac{2}{3} $$
対数関数とそのグラフ
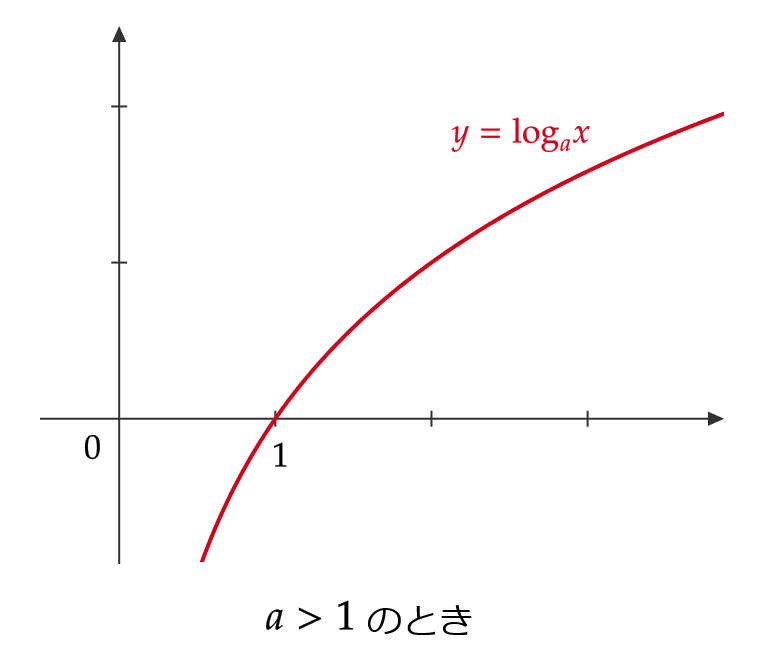
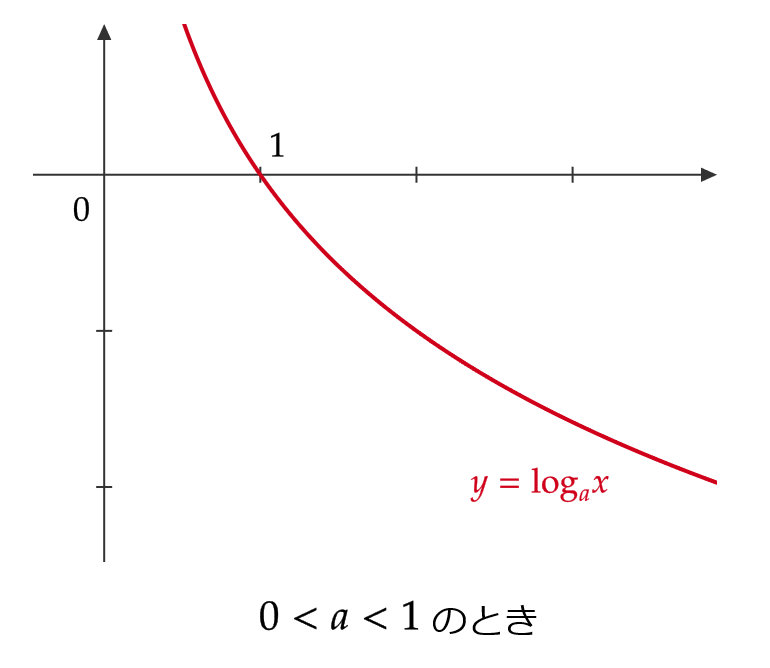
\( a>0, \ a\not=1 \) のとき、対数関数 \( y=\log_ax \) のグラフを考えていきます。
\( x \) について解くと、 \( x=a^y \) であるので、 \( y=\log_ax \) の逆関数は \( y=a^x \) となります。
よって、 \( y=\log_ax \) は \( y=a^x \) のグラフを \( y=x \) に関して対称にしたグラフとなります。
今回はここまでです。お疲れ様でした。また次回にお会いしましょう。

